可预见大客流下的跳停轨交列车时刻表优化

陈吉怀，赵 星

( 河海大学 土木与交通学院，江苏 南京 210098)

城市交通需求逐年扩大，城市轨道交通系统作为缓解交通拥堵的重要方式，凭借其快速、舒适、运量大、低延误以及安全性高等优点在城市公交系统中发挥着重要作用。十三五期间提出，预计2020年轨道交通运营里程将达6 000 km，我国轨道交通正迎来前所未有的大发展时代。

乘客出行需求的旺盛增长势必会导致轨道交通系统内人流密集拥挤，甚至出现滞留情况，大大增加了安全隐患。对大客流，尤其是可预见性大客流的控制便显得尤为重要，韦永佳、周云娣、李佳芸[1-3]分别从不同城市实际出发，针对特定情形分析大客流特征，并对大客流控制措施进行一定的探讨。赵鹏、姚向明[4-5]等人则以各站不同时段的限流率为决策变量分别建立了地铁单线和线网的大客流线性控制模型，可计算乘客延误时间最小优化目标下的车站进站人数控制策略。

轨道交通相关部门也制定了一系列列车运行调整措施来限制事故发生[6]，“跳停”便是其中重要的一项，在部分国际发达城市中已有应用，如巴黎、莫斯科、旧金山的地铁系统，均采用非站站停的特殊停站方式，根据客流分布的特征，选择不同的列车停站方案关系到列车运行组织的合理性、系统服务水平等[7]。郭婧、屈明月[8-9]构建了“跳停”的评价体系，论证跳停的可行性和适用性，王婵婵等[10]则指出了跳停可能带来的一些负面影响。

作为交通运输中的重要优化应用，列车时刻表问题在最近几十年内备受关注。列车时刻表规定各次列车在各个区间的运行速度、在车站的到发和停留时间，是城市轨道交通运营的服务提供者和乘客之间的重要桥梁。列车运营效率导向和出行需求导向是当前研究的两大主要方向[11-12]，学者们或利用图论、运筹学等建模方法[13]，或利用现代智能优化算法求解[14-15]，希望谋求一种乘客出行与列车运营效率高且经济的方法，优化列车时刻表。

基于对以上三点的总结分析，本文提出一种考虑可预见性大客流的跳停轨道交通列车时刻表优化方法。针对轨道交通某时段的特定OD——由起点至终点的交通出行量，使用遗传算法选择出使得乘客总等待时间最短的列车跳停计划，进而确定列车开行计划。利用此方法，可以较好地使用历史数据推衍，得到未来针对可预见性大客流的列车开行计划，通过改进跳停计划以达到乘客更优出行，对轨道交通列车运行调度有实际指导意义。

1 问题描述

考虑一条S座车站城市轨道交通线路，如图1所示，本研究中仅考虑列车的单向行驶，即研究时段内所有列车均由第1站出发，至第S站停止。根据既定客流量，调节不同车次在不同站点的跳停情况以及停车时间长短，以达到最小化乘客总候车时间的目的。

图1 列车行进示意Fig.1 Schematic diagram of train travel

根据城市轨道交通列车运营实践，提出如下假设：

假设1：所提供的总列车容量大于或等于总乘客需求，并且最后一列车在每个站都停靠并且在研究时段的准确结束时刻T离开第一站，这种假设可以确保所有乘客在规划期间到达目的地站。

假设2：乘客已知特定列车的跳停模式，若来车不在某乘客的目的地站点停车，那么该乘客会继续等待直到所需列车到来。

假设3：某一辆列车的容量已达饱和而仍有乘客尚未进入列车时，这些乘客会原地等待，直到下辆列车到达。

假设4：优化模型遵循乘客先进先出原则，即首先到达站点的乘客可优先乘车，当假设3情况发生时，乘客总候车时间会受到上车顺序的影响，因此在模拟过程中有必要假设所有乘客均遵循先进先出原则，否则会复杂化计算过程。

2 列车时刻表优化模型构建

2.1 数学符号

2.1.1参数

除与列车时刻表直接相关的量为变量外，其他量均为参数，是定值(例如列车数、车站数和列车容量等)或者有固定的取值范围(例如列车最短最长停留时间和列车间最小间隔等)，具体罗列如下。

(0,T)———列车运营时段;t———时间指数,t∈(0,T);J———列车编号;N———列车总数;S———车站编号,其中U为出发站,V为终点站;PU,V(t)———t时刻从U站至V站的人数;Z———乘客总候车时间;z———单个乘客候车时间;C———列车容量;RU———车辆从U站到U+1站的自由行驶时间;D1J———J车离开第一站的时间;θsectionmin———在同一区间的两个连续列车之间的预定最小间隔;θstationmin———在同一站点的两个连续列车之间的预定最小间隔;λmin———列车在车站预定的最短停留时间;λmax———列车在车站预定的最长停留时间;Q———列车实际在车人数;

2.1.2变量

本文最终优化结果是得到了列车在不同站的停车时间，故停留时间为决策变量，随停留时间变化而相应变化的到站和离站时间为中间变量。

2.2 目标函数

(1)

又设t时刻到达U站欲前往V站的乘客人数为PU,V(t)，他们全部都会乘坐J车离开，则该群人的总等待时间为，

(2)

将时间由t时刻扩展到整个研究期限(0，T)内，乘客数由一位乘客扩展至研究期限内所有乘客，则乘客的总等待时间可表示为，

(3)

2.3 约束条件

列车容量约束。每辆车都有固定的满载量，为方便起见，每辆车的满载量都设为一固定值C，列车上的总人数不可超过规定阈值，若某一辆列车的容量已达饱和而仍有乘客尚未进入列车时，这些乘客会原地等待，直到下辆列车到达。列车从U站出发后留在J车中的乘客数为,

(4)

则容量约束为，

Q≤C。

(5)

链接约束。不考虑列车行驶过程中的额外加减速时间以及缓冲时间，则列车到站时间等于该列车从上一站的出发时间加上两站间的列车行程时间。

(6)

列车发车时间等于列车到达时间加列车在本站停留时间。

(7)

(8)

(9)

基于站的车头时距约束是为了确保在一小段时间内一站中仅有一列火车停靠。

(10)

可行域约束。设λmin，λmax为列车在车站预定的最短和最长停留时间，须确保每个站的列车停留时间具有可行范围。

(11)

综上，本文构建了考虑可预见性大客流的跳停轨道交通列车时刻表优化模型，目标函数为式(3)，约束条件为式(5)到式(11)。

3 算法设计

在模型中共考虑J列车，S个站点，除去起点站和终点站之后余(S-2)个站，每列车在每个站点的停车方式共有9种。若用穷举法来求解，则需列举9J×S种可能，这显然大大超出当前计算机的运能，故本模型利用遗传算法求解优化目标。遗传算法是基于自然种群遗传变异机制的一种有效的智能搜索算法，其模拟达尔文生物进化和自然消亡的过程。该算法具有自组织性，自学习性，在求解轨道交通车辆调度和列车运行时刻表等问题时表现出较强的优越性。

1)染色体编码。遗传算法需要将所有变量转换为基因，并按照一定顺序编入染色体。本模型中所求为各列车在各站的停车时间为未知量，起点站和终点站不在考虑范围内，故基因共有J×(S-2)个。

2)初始种群生成。种群数量为30，使用浮点法随机生成的列车停车时间组合为染色体并检验其可行性。

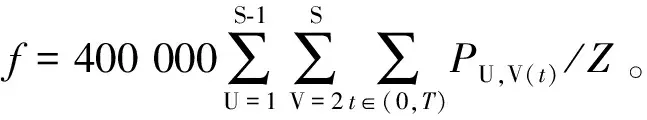
4)选择。采用轮盘赌对个体进行选择：

(1)种群中所有个体的适应度之和∑f；

(2)每一个个体适应度与总适应度之比，作为该个体的被选择的概率pr=fr/∑f；

(3)在[0，1]区间内产生一个随机数h，若pr-1≤h≤pr，则选择第r个个体，重复进行30次，可选择出30个个体进入第5、6步。

5)交叉。设置交叉概率Pc=0.8，将上一代个体按适应度大小排序，前十位不进行交叉，发生交叉的个体随机配对，确定交叉点位置和进行部分基因交换。产生的子代需通过约束条件检验方可保留。

6)变异。设置变异概率Pv=0.8，上一代个体中适应度前十位的不进行变异，根据变异概率随机确定部分个体变异，改变其某个基因。产生的子代需通过约束条件检验方可保留。

7)迭代求解。设置迭代次数Gen=200次。

其中，乘客上下车逻辑及约束条件检验如下：

第1步，随机生成每站的停车时间矩阵。第1站停车时间必定为0，问题中延误时间等于列车发车时间减乘客进站时间，因此跟列车到达时间无关，故第S站不用考虑。共有J辆车、(S-2)个站，因此停车时间矩阵为一个J×(S-2)矩阵，每一行表示每辆车1→(S-2)在站的停车时间，每一列代表同一站不同车次的停车时间。停车时间为0、30、60、90……240 s，当出现0 s时意味着跳过停车。

第2步，根据停车时间矩阵和每辆车的发车时间计算每站每辆车的到达时间矩阵和出发时间矩阵，均为J×(S-2)矩阵。

第4步，不考虑每量车的容量和无法停车上人的问题，根据每辆车发车的时间段，将客流数据分配到对应车次的时间段内，得到一个A{J，(S-2)}(N-4)的元胞数组，(N-4)矩阵为第(J-1)列车在第S站发车后，第J列车在第S站发车前时间段内进入第S站的所有人的信息，即在理想情况下，在这个时间段内进站的人都应该上到第J列车。

第5步，不停站的处理。如果第J列车在第S站不停，那么在对应时间段内进站的人都不能上第J列车，只能继续等第(J+1)列，因此，在乘客信息的元胞数组中，需将A{J，S}中所有的数据移动到A{J+1，S}中，并将A{J，S}清空。对于第J列车，如果它不在第S站停车，那么在第S站之前需要查找是否有目的地是第S站的乘客，如果有，将这名乘客移支到第(J+1)列车，第S站对应的A{J+1，S}中去。

第6步，有人下车的处理。设第J列车从第(S-1)站出发后，已经在车里的人中有目的地是第S站的，则当车到达第S站时，车上的人员信息中删除要下车的人的信息，同时统计到第S站时、到站的人下车后、没开始上人前车里的人的数量。

第7步，上车人数超过列车的满载量的处理。将到站后上人前列车内的人数与计划在本站上车的人数相加，与列车容量相比较，若准备上车人数加列车原有人数超过列车容量，那么按照先来后到的顺序将多出来的乘客信息移动到第(J+1)辆车。

第8步，重复5—7步，直到遍历完整个J×(S-2)矩阵，便得到了当前停车时间矩阵下所有乘客的乘车信息。

第9步，根据所有乘客的乘车信息计算总的延误时间以及平均延误时间。

算法流程如图2所示：

图2 算法流程图Fig.2 Algorithm flow chart

4 实例分析

4.1 线路背景介绍

南京地铁S1号线，又称机场线，于2014年7月1日正式投入运营使用，是南京城市轨道交通路网中一条南北走向的线路，标志色为宝石绿色。地铁S1号线先后经过雨花台区和江宁区，线路北起南京最大的高铁站南京南站，一路南下经过江宁东山片区西侧、秣陵片区、江宁经济技术开发区、禄口新城，南至空港新城江宁站。

地铁S1号线全长37.3 km，其中地下段19.8 km、过渡段0.7 km、高架段16.8 km；共设置8座车站，其中地下站6座、高架站2座，分别为南京南站、翠屏山站、河海大学-佛城西路站、吉印大道站、正方中路站、翔宇路北站、翔宇路南站和禄口机场站；列车采用B型鼓形列车6节编组，最高运行时速100 km/h，由中国中车南京浦镇车辆有限公司制造。

截止至2019年4月，南京地铁S1号线平均日客流达9.3万人次，其最高单日线路客运量为13.8万人次，于2019年4月4日诞生。禄口机场为南京最大的机场，南京南站为南京最大的高铁站，S1号线的链接着两个重要的大客流集散地，是南京通往外地的重要交通枢纽，易出现可预见性大客流。根据本文需要和可选的实际情况，在本文中，仅仅考虑从禄口机场站首发，至南京南站位终点的单向列车表，选取2016年十一期间早高峰7：00—8：00时段进行研究。

4.2 基本信息及计算结果

研究区间为早高峰一个小时，故T=60 min，t∈(0，60)。

南京地铁S1号线共有S=8个站，分别为禄口机场站、翔宇路南站、翔宇路北站、正方中路站、吉印大道站、河海大学-佛城西路站、翠屏山站和南京南站。

假设列车7：00准时开行第一班，每十分钟开行一班，一小时内共计N=7辆车。

车辆从U站到U+1站的自由行驶时间RU如表1所示。

PU,V(t)即每时刻的乘客OD如表2所示，第一列为进站分钟，第二列为进站秒数，第三列为进站点，第四列为出站点，原始数据需简单处理后使用：第一列和第二列不在(0，60)的需排除；进站点与出站点相同的需排除；因仅考虑单向行驶，故出站点在进站点之前的需排除；出站点不在S1号线上时，认为出站点在S1号线的终点站即南京南站，共计4 937人。

每辆车的满载量C=1 000人。

列车在车站预定的最短停留时间λmin=0 s，列车在车站预定的最长停留时间λmax=240 s。

停车时间为公差为30 s的等差数列，0、30、60、90……240 s，当出现0 s时意味着跳过停车。

表1 相邻车站的自由行驶时间Tab.1 Free travel time of near station min

遗传算法中，染色体长度为7×6=42，种群数量POP-SIZE=30，交叉概率Pc=0.8，变异概率Pv=0.8，3点变异，在交叉和变异步骤中还加入了较优个体保留原则，即交叉变异前适应度前十位的个体直接进入子代，迭代次数Gen=200次。

表2 每时刻乘客ODTab.2 Passengers’ OD of every moment

表3 列车在每一站的跳停模式与优化停留时间Tab.3 The train's skip-stop pattern and optimization stay time at each station min

将表3中的列车调度情况绘制成列车开行计划图，横坐标为S1号线的各个停靠站点，共包含8个车站，纵坐标为时间，研究时间从0 min开始，折线即为列车的优化运行轨迹，如图3所示。

图3 优化列车调度Fig.3 Optimized train scheduling

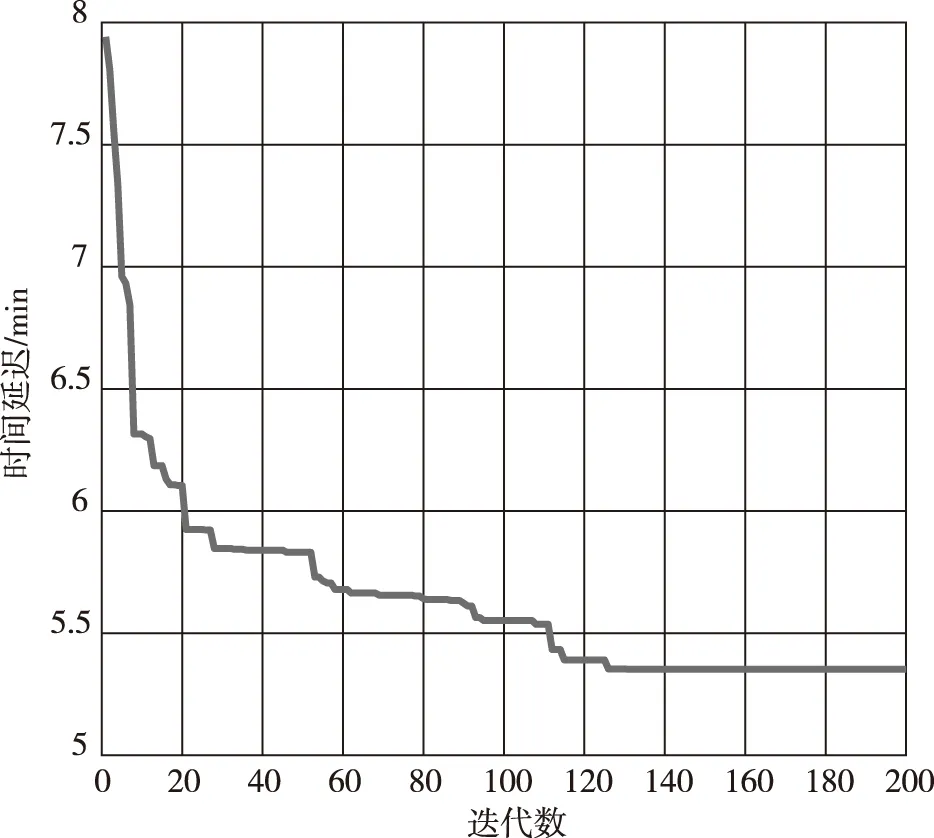
图4 每一代中最小时间延迟变化曲线Fig.4 Minimum time delay change in each generation

为验证本文模型的优点所在，利用现有基础数据，计算未经优化的乘客总等待时间，在实际情况中，采用列车在每个站点均停车的模式，固定每辆车在每个站点均停靠1.0 min，其余条件与本文的模型相同，由于最后一班列车的运行时间减少，导致研究时段内总客流量减少至4 797人，所得目标函数结果为26 638 min，平均每位乘客的等待时间为5.553 min。优化模型与未优化模型相比，平均每位乘客的等待时间由5.553 min减至5.352 min，减少了0.201 min，效果显著。

为验证增加车辆停车时间是否导致了乘客总在车时间相应增加，需进一步对比乘客平均总在车时间。乘客刷卡数据和列车运行时刻表确定后，乘客的总在车时间也相应确定。经计算得，实际情况下，乘客平均总在车时间为13.176 min，优化后，乘客平均总在车时间为13.198 min，时间增加了0.022 min，影响较小。

5 结语

本文主要讨论了存在可预见性大客流以及列车跳停情况下，通过优化轨道交通列车时刻表，来提高乘客的总体出行效率。构建了优化列车时刻表模型，以乘客总候车时间为优化目标，采用遗传算法求解了优化问题。最后，根据南京地铁S1号线的实际客流需求数据，设计了仿真实验，验证了算法与模型的有效可行性，对轨道交通的运营和提高乘客出行舒适度有现实指导意义。

本文的模型实现是以可预见性大客流为前提，若能统计多年来出现的大客流信息，例如，十一黄金周期间、某地举办大型活动时的客流量，形成数据库，当日后出现相似情形时，便可以提前预警做出应对。

论文目前仅考虑了单向单线列车的时刻表优化，而随着轨道交通系统的发展，有必要进一步考虑成网的双向列车时刻表优化问题，使问题更贴近实际。