基于改进Hotelling模型的中欧班列运营商竞合关系研究

李玉民，潘晓景，王博，代冬霞

基于改进Hotelling模型的中欧班列运营商竞合关系研究

李玉民，潘晓景，王博，代冬霞

(郑州大学 管理工程学院，河南 郑州 450001)

针对中欧班列运营商间竞争与合作并存发展问题，综合考虑集装箱运输成本、地理位置、运输费率、利润分配占比等因素，利用改进Hotelling模型，构建了完全竞争模式(NC)和半合作模式(HC)2种竞合模式，并通过对比、仿真分析研究2种竞合模式下班列运营商的最优决策。结果表明：1) 只有两方班列运营商的利润分配占比同时满足一定条件时，二者方能合作结成中欧班列运营商联盟。2) 班列运营商为获得更大的市场份额，若合作后的集装箱运输成本大于阈值，竞争是最优策略；反之，合作是最优策略。3) 当班列运营商的集装箱运输成本接近时，采取合作策略能提高中欧班列运营商联盟的均衡利润。

中欧班列运营商；竞合关系；改进Hotelling模型

中欧班列(CHINA RAILWAY Express)是“一带一路”实现设施互联互通的重要陆路运输通道。为促进中欧班列共赢发展，有关部门出台了一系列方案，例如：《中欧班列建设发展规划2016—2020》中强调要完善合作机制、加强分工协作、避免无序竞争，推动形成联动发展新格局；《中欧班列高质量发展倡议书》中强调在保持地方特色的基础上整合线路、整合节点，合作开行大公共班列和阶梯班列。2019年中欧班列开行8 225列，发运72.5万标箱，重箱率达94%，但仍存在竞争激烈、缺乏合作、协调度低等问题[1]，因此，本文从竞争、合作并存发展的角度，研究中欧班列运营商(以下简称班列运营商)间的竞合关系，为促进中欧班列良好发展提供决策参考。竞合概念(co-opetition)是不同关系网络中蕴含竞争与合作的关系集合，且表现为竞争和合作的交互作用[2]。为促进中欧班列健康、有序、快速、可持续发展，国内外学者在中欧班列竞合发展方面进行了积极探索，取得了不少成果。1) 竞争关系研究。有学者研究中欧班列与其他运输方式的竞争，如LI等[3]基于随机效用理论的离散选择模型研究中欧班列与航运间的市场份额竞争；曾玮等[4]基于显示性比较优势理论研究中欧班列与海陆联运、航空的竞争。部分学者研究不同中欧班列间的竞争，如WANG等[5]认为设施联通、运输价格、货源及政治环境将影响中欧班列间的竞争；付新平等[6]基于价值成本量研究中欧班列线路间的竞争。2) 合作关系研究。目前多数学者主张通过建立中转、集结中心进行中欧班列间的合作，如ZHAO等[7]运用TOPSIS方法选择中欧班列集结中心城市；闫伟等[8]研究中欧班列间平均旅行速度、货物时间价值对集结运输合作模式的影响；江志娟等[9]提出成立中转联运枢纽城市进行货物集散、中转的合作方式；李天昊等[10]对中欧班列网络赋予不同节点功能来合作组织运输。但上述成果仍存在不足，如只从竞争或只从合作角度考虑班列运营商间的关系，但没有考虑竞争与合作并存时的影响，即班列运营商间的竞合关系；班列运营商之间联盟的合作方式鲜有研究；没有考虑从货源地到班列运营商始发站的地理位置距离的影响。所以本文提出运用改进Hotelling模型，以多个班列运营商间竞合关系为研究对象，考虑竞争与合作并存的交互作用以及班列运营商的地理位置差异，研究班列运营商利润最大化时的最优策略，以期为促进中欧班列长期稳定、健康、可持续发展提供参考。

1 问题描述与假设

1.1 问题描述

不失一般性，考虑存在3个班列运营商共同提供从中国到欧洲的货运服务，班列运营商的集装箱运输成本、地理位置、运输费率、利润分配占比等因素综合影响其最优运输价格、最优市场份额、最大利润。中欧班列始发站、目的站的集疏运情况类似，且中国是中欧班列的主要驱动方，所以以中国始发站为例，其研究结论也适用于欧洲始发站。考虑班列运营商间只有竞争及多个班列运营商合作的情形，主要研究2种竞合模式如图1所示。第1种是完全竞争模式(Non-cooperative，NC)，三方班列运营商间没有合作，只有竞争；第2种是半合作模式(Half-cooperative，HC)，其中2个邻近班列运营商相互合作结成中欧班列运营商联盟，与第3个班列运营商相互竞争。探讨班列运营商何种条件下适合采取竞争策略、何种条件下适合采取合作策略，以及中欧班列运营商联盟策略是否有效。

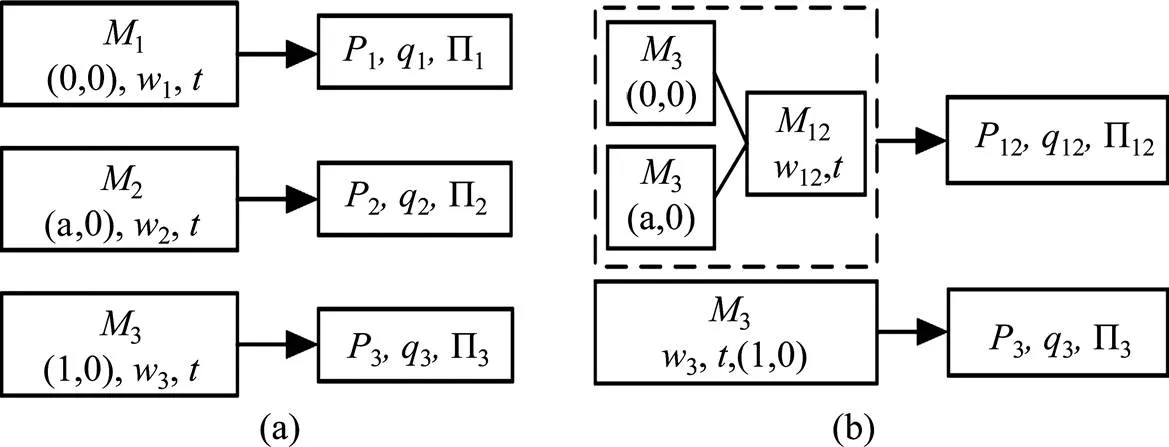
(a) 非合作模式(NC)；(b) 半合作模式(HC)

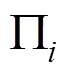
1.2 问题假设

假设1：假设3个班列运营商M按其相对位置转换在轴[0,1]的线性市场，则M的位置分别为(,0)，1=0，2=，3=1，0＜＜1。

假设2：假设发货人均匀分布在密度为1的[0,1]区间，发货人有单位集装箱需求，超过单位集装箱按多位发货人处理。单位集装箱运输服务完成，对发货人产生保留效用0，假设0足够大，使任何位置发货人都会选择一方班列运营商服务。

假设3：假设货物从货源地到始发站的成本与陆上运输距离成比例。

假设4：假设发货人、班列运营商理性且信息完全公开，市场有序。

假设5：为推进中欧班列的市场化运营，政府补贴将逐渐退出，具有暂时性，故不考虑政府补贴政策的影响。

2 模型构建

班列运营商具有以下特点：班列运营商始发站地理位置固定；发货人向班列运营商支付运费，班列运营商委托中国铁路总公司运输并支付费用；发货人选择班列运营商需要综合考虑班列运营商的运输价格和发货人将货物运输至始发站的运输费用。Hotelling模型将消费者的地理位置差异视为产品差异，适合解决竞争者间的运输距离差异问 题[11]。本文将经典Hotelling模型的两方竞争博弈扩展至三方[12]，结合班列运营商的特点，构建出2种班列运营商间的竞合模式，分别是完全竞争模式(NC)、半合作模式(HC)。

2.1 完全竞争模式(NC)

完全竞争模式下，3个班列运营商通过运输价格和地理位置距离的差异进行竞争。当发货人位于横坐标，综合考虑班列运营商1，2和3的运输价格、地理位置，利用改进Hotelling模型，得出1，2和3的效用[13]分别是：

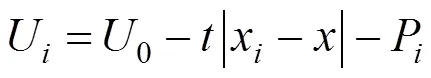
所以，存在位置1，发货人选择1和2效用无差异；存在位置2，发货人选择2和3效用无差异，如图2所示，完全竞争模式下Hotelling线段示意图。此时，由1=2，2=3解得：

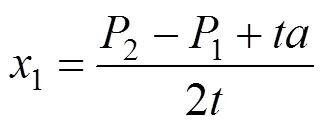
发货人根据效用值最大化原则选择1或2或3的运输服务[14]。所以在区间[0,1]的发货人将选择1的运输服务；在区间[1,2]的发货人将选择2的运输服务；在区间[2,1]的发货人将选择3的运输服务。又因为发货人均匀分布在密度为1的[0,1]区间，且发货人有单位集装箱需求，则发货人对班列运营商M的总需求量就等于M的市场份额，所以完全竞争模式下M的市场份额q分别为：

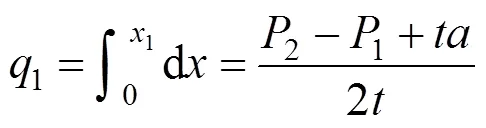
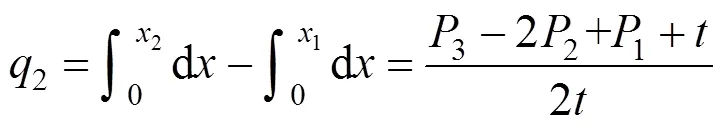
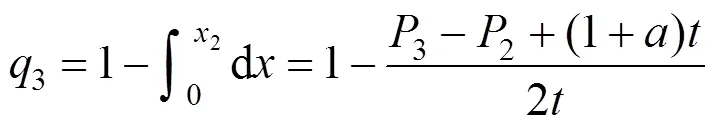
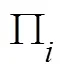
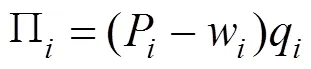
完全竞争模式下，M独立决策，以自身利润最大化为目标，得M最优反应函数：

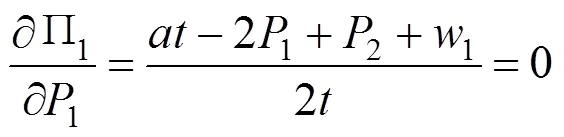
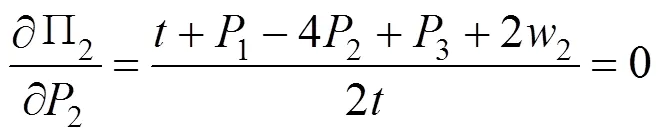
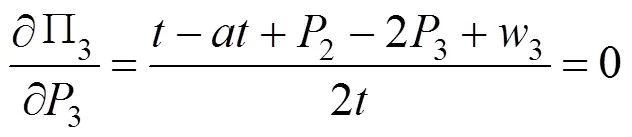
联立式(6)～(8)求解，得完全竞争模式下班列运营商的均衡解(用*表示)如表1所示，其中均衡价格代表班列运营商利润最大化时最优运输价格，均衡市场份额代表班列运营商利润最大化时占有的最优市场份额，均衡利润代表班列运营商获得的最大利润。

2.2 半合作模式(HC)

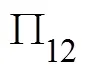
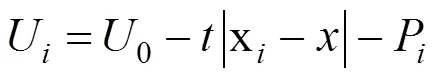
所以，存在位置23，发货人选择12或3效用无差异，如图3所示，半合作模式下Hotelling线段示意图。此时，由12=3解得：

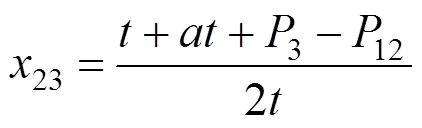
发货人根据效用值最大化原则选择12或3的运输服务。所以在区间[0,23]的发货人将选择12的运输服务，在区间[23,1]的发货人将选择3的运输服务。又因为发货人均匀分布在密度为1的[0,1]区间，且发货人有单位集装箱需求，则市场上发货人对12(或3)的总需求量就等于12(或3)市场份额，所以半合作模式下12和3的市场份额q分别为：

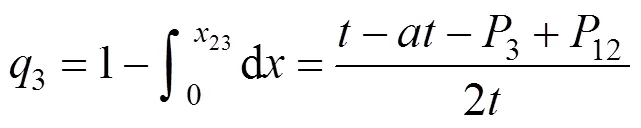
图3 半合作模式下Hotelling线段示意图

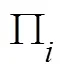
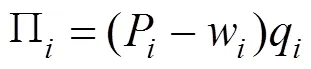
半合作模式下12采用集中决策，以共同利润最大化为目标，3独立决策，以自身利润最大化为目标，得12和3最优反应函数：

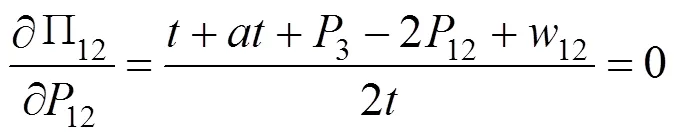
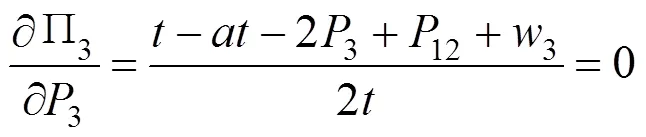
联立公式(13)～(14)，得半合作模式下12和3的均衡解(用**表示)如表1所示。

表1 NC和HC模式下的均衡解

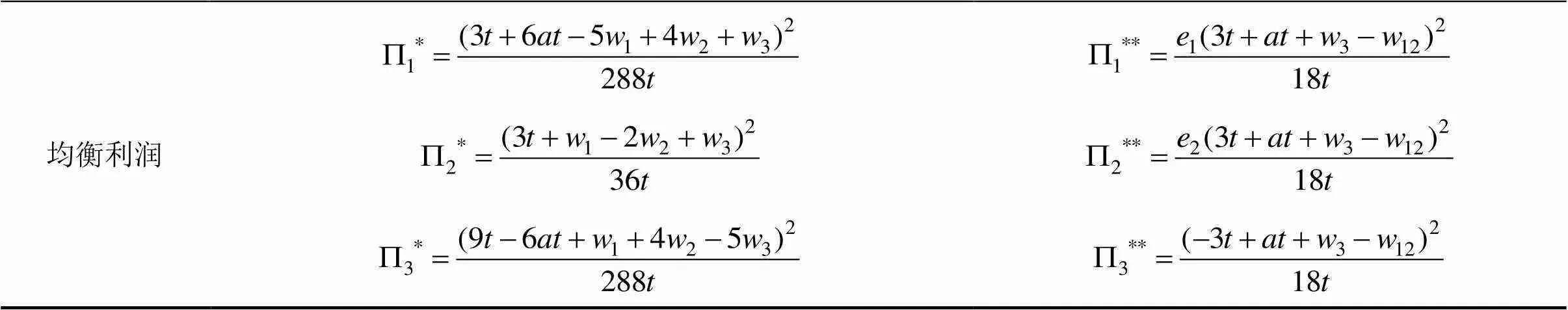
均衡利润

3 均衡结果分析

命题1：任一班列运营商的集装箱运输成本增加均会引起自身的均衡价格提高、均衡市场份额降低，并引起竞争对手的均衡价格提高、均衡市场份额提高。

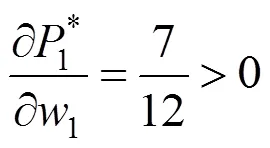
证毕。命题1说明，任一班列运营商的集装箱运输成本增加，会将这一部分成本转移至运输价格，引起自身均衡价格提高，导致自身竞争力减弱，部分发货人将选择其他班列运营商，引起自身均衡市场份额减少，竞争对手均衡市场份额提高；同时，竞争对手的竞争力增强后，竞争对手倾向于提高均衡价格以获得更大利润。

命题2：随着运输费率t增加、相邻班列运营商地理位置距离增大，班列运营商的均衡价格均会提高。

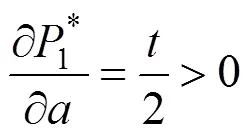
命题3：当3的集装箱运输成本降低，在NC和HC 2种模式下3的均衡市场份额都提高，但NC模式下3的均衡市场份额提高幅度更大。

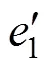
命题6：当班列运营商的集装箱运输成本接近时，班列运营商采取合作策略的均衡利润之和高于竞争策略的均衡利润之和，中欧班列运营商联盟策略有效。

4 仿真分析

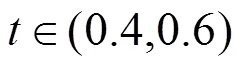
表2 中欧班列运营商始发站相对位置

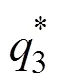
最后数值仿真，当=0.42，=522.5USD/ (FEU·km)，1=4 500USD/FEU，2=4 750USD/FEU，1=4 600 USD/FEU，12=4 400USD/FEU，用MATHMATICA软件进行算例仿真，结果如表3所示。

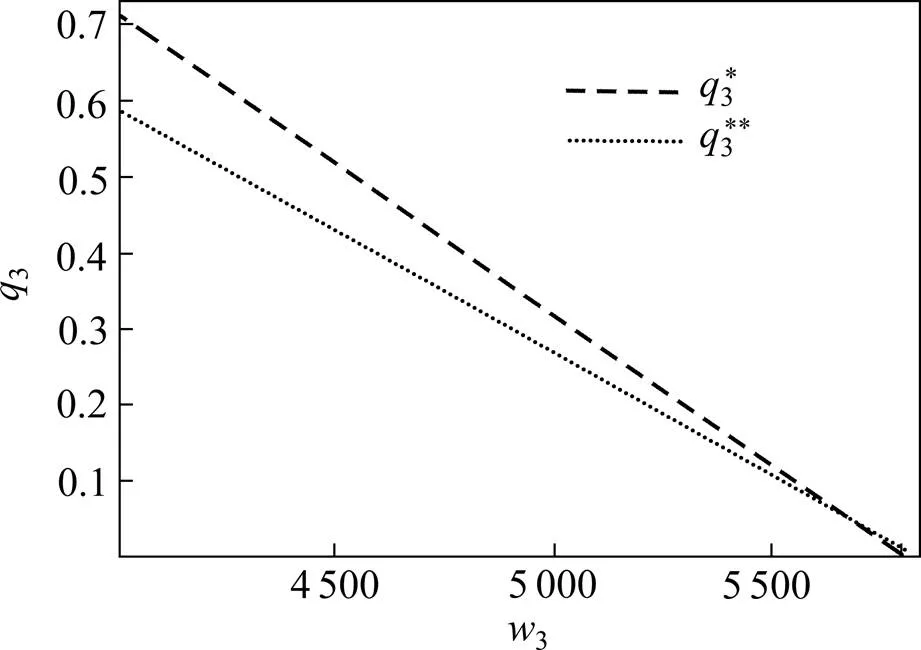
图4 NC和HC模式下w3对q3的影响

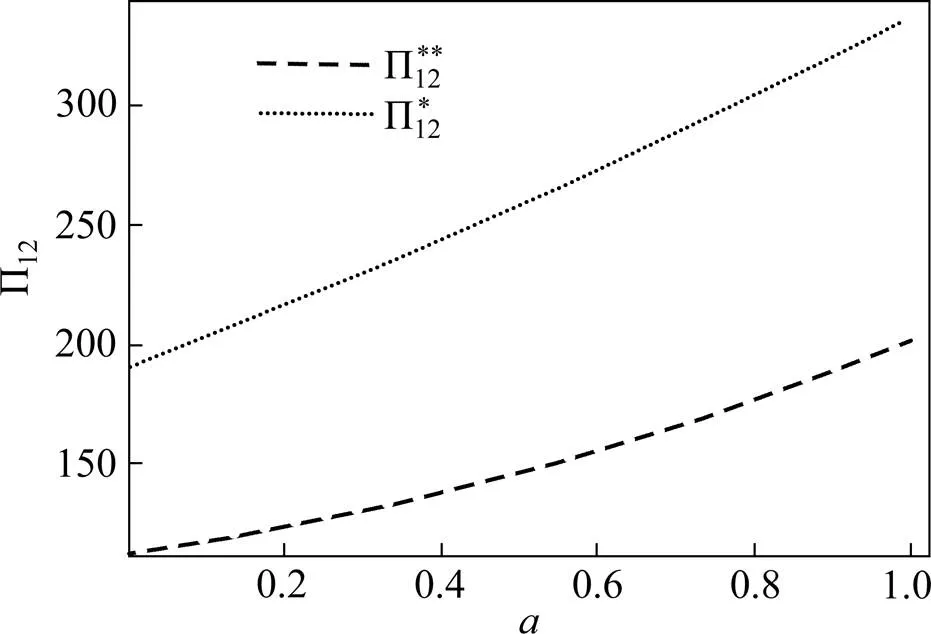
图5 NC和HC模式下a对的影响

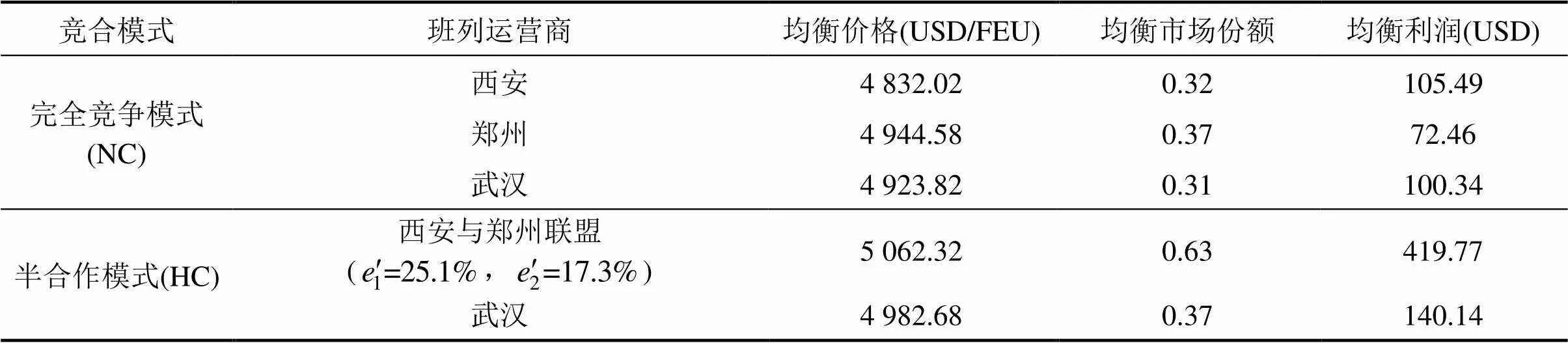
表3 算例仿真结果

注：设总市场份额为1。

由表4可知，当西安与郑州联盟后，西安的均衡利润分配占比超过25.1%，且郑州的均衡利润分配占比超过17.3%，二者合作后的均衡利润才会大于竞争时的均衡利润，即二者才会采取合作策略结成中欧班列运营商联盟(验证命题4)。相比完全竞争模式，半合作模式下西安和郑州相互合作结成联盟后的均衡利润提高。

5 结论

1) 任一班列运营商的集装箱运输成本增加均会引起自身的均衡价格提高、均衡市场份额降低，并引起竞争对手的均衡价格提高、均衡市场份额提高。因此，建议班列运营商能统一对国外铁路运输线路代理商谈判，并促进资源与技术共享，来降低集装箱运输成本，最终实现中欧班列整体的均衡价格降低。

2) 随着运输费率的增加，班列运营商的均衡价格也会得到提高。因此，建议我国有关部门不断完善始发站的集疏运体系，进一步降低运输费率，从而实现中欧班列的均衡价格降低。

3) 只有班列运营商的利润分配占比满足一定条件时，合作后才会获得更大的均衡利润，否则，合作后的均衡利润反而减少。当班列运营商的利润分配占比均超过了各自利润分配占比的最小值时，二者方能合作结成中欧班列运营商联盟。因此，建议班列运营商在达成联盟之前，事先预测各自的利润分配占比的最小值，从而合理分配利润，使得合作后双方的均衡利润均增加，实现共赢。

4) 当合作后的集装箱运输成本大于阈值，采取合作策略后中欧班列运营商联盟的均衡市场份额反而缩小，此时，班列运营商间竞争是最优策略；当合作后的集装箱运输成本小于阈值，采取合作策略后中欧班列运营商联盟的均衡市场份额扩大，此时，班列运营商间合作是最优策略。因此，建议班列运营商根据合作后集装箱运输成本的阈值，事先决策最优策略。

5) 当班列运营商的集装箱运输成本接近时，采取合作策略提高中欧班列运营商联盟的均衡利润，也说明了中欧班列运营商联盟策略有效。因此，建议健全联盟制度，探索合作关系的激励机制，同时也应该避免因联盟势力过大形成垄断，扰乱正常市场价格。

[1] ZHANG Zhijia, LI Xiaohong, ZHANG Zhiwei. Analysis on the developing situation of China Railway Express[J]. IOP Conference Series: Materials Science and Engineering, 2019, 612(2): 32−98.

[2] Fernandez A S, Roy F L, Gnyawali D R. Sources and management of tension in co-opetition case evidence from telecommunications satellites manufacturing in Europe[J]. Industrial Marketing Management, 2014, 43(2): 222−235.

[3] LI Shiqi, LANG Maoxiang, YU Xueqiao, et al. A sustainable transport competitiveness analysis of the China Railway Express in the context of the belt and road initiative[J]. Sustainability, 2019, 11(10): 1−30.

[4] 曾玮, 毛保华. 基于货物价值特性的国际集装箱班列竞争力分析[J]. 交通运输系统工程与信息, 2019, 19(2): 37−45. ZENG Wei, MAO Baohua. A competitiveness analysis of international container transport based on value of goods[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(2): 37−45.

[5] WANG Jiaoe, JIAO Jingjuan, MA Li. An organizational model and border port hinterlands for the China-Europe Railway Express[J]. Journal of Geographical Sciences, 2018, 28(9): 1275−1287.

[6] 付新平, 张雪, 邹敏, 等. 基于价值量模型的中欧班列经济性比较分析[J]. 铁道运输与经济, 2016, 38(11): 1−5. FU Xinping, ZHANG Xue, ZOU Min, et al. Analysis on economics of China-Europe Block Trains based on the value model[J]. Railway Transport and Economy, 2016, 38(11): 1−5.

[7] ZHAO Laijun, ZHAO Yue, HU Qingmi, et al. Evaluation of consolidation center cargo capacity and locations for China railway express[J]. Transportation Research Part E:Logistics and Transportation Review, 2017, 117(C): 58−81

[8] 闫伟, 朱晓宁, 邓宇君, 等. 中欧班列去程运输组织优化模型[J]. 铁道学报, 2019, 41(2): 1−7. YAN Wei, ZHU Xiaoning, DENG Yujun, et al. Optimization model of outbound transportation organization for China Railway Express[J]. Journal of the China Railway Society, 2019, 41(2): 1−7.

[9] 江志娟, 关高峰. “一带一路”倡议下的国际通道中转枢纽设计模型和算法[J]. 公路交通科技, 2017, 34(10): 135−143. JIANG Zhijuan, GUAN Gaofeng. A model and an algorithm for designing transit hub of international channel under the belt and road initiative[J]. Journal of Highway and Transportation Research and Development, 2017, 34(10): 135−143.

[10] 李天昊, 魏玉光. 基于节点功能设计的中欧班列网络开行方案模型[J]. 交通运输系统工程与信息, 2018, 18(增1): 35−43. LI Tianhao, WEI Yuguang. Train plan model of China railway express network based on node function design[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(Suppl 1): 35−43.

[11] Harold. Hotelling stability in competition[J]. Economic Journal, 1929, 39(153): 41−57.

[12] 范洋, 高田义, 乔晗. 基于博弈模型的港口群内竞争合作研究——以黄海地区为例[J]. 系统工程理论与实践, 2015, 35(4): 955−964. FAN Yang, GAO Tianyi, JIAO Han. Competition and collaborative strategies within ports cluster in Huanghai area-a game theory approach[J]. Systems Engineering- Theory ＆Practice, 2015, 35(4): 955−964.

[13] 王焯, 蹇明. 基于博弈论的高速铁路与航空货运定价影响研究[J]. 铁道科学与工程学报, 2019, 16(10): 2414−2420. WANG Zhuo, JIAN Ming. Research on the influence of high-speed railway and air cargo pricing based on game theory[J]. Journal of Railway Science and Engineering, 2019, 16(10): 2414−2420.

[14] 黎继子, 汪忠瑞, 刘春玲, 等. 供应链跨国进入模式下的Hotelling决策模型及策略[J]. 管理工程学报, 2018, 32(3): 162−170. LI Jizi, WANG Zhongrui, LIU Chunling, et al. Hotelling decision making model and tactics for supply chain with transnational entry model[J]. Journal of Industrial Engineering Management, 2018, 32(3): 162−170.

Research on the co-opetition of the CHINA-EUROPE RAILWAY Express operator based on the extended Hotelling model

LI Yumin, PAN Xiaojing, WANG Bo, DAI Dongxia

(School of Management Engineering, Zhengzhou University, Zhengzhou 450001, China)

In view of the coexistence of competition and cooperation, which is the existing problem of CHINA-EUROPE RAILWAY Express operator. This paper considered the influence of container transportation costs, geographical differences, terminal transportation rates and proportion of profit distribution, and made full use of the extended Hotelling model, built two types of co-opetition models which were the non-cooperative model (NC) and half-cooperative model (HC). Such two models were compared and the simulation analysis was performed to make optimal decisions. The results are show blow that: 1) Only when the proportion of the profit distribution of the CHINA-EUROPE RAILWAY Express operator meets certain conditions can a CHINA-EUROPE RAILWAY Express operator alliance be formed. 2) When the container transportation costs in cooperation are greater than the threshold, CHINA-EUROPE RAILWAY Express operator wants to get greater market share, competition is the optimal strategy; otherwise, cooperation is the optimal strategy. 3) When the container transportation costs of the CHINA-EUROPE RAILWAY Expressoperator are approaching, adopting a cooperative strategy can increase the profits of the CHINA-EUROPE RAILWAY Express operator alliance.

CHINA RAILWAY Express operator; co-opetition; the extended Hotelling model

10.19713/j.cnki.43−1423/u.T20200569

U-9；F53

A

1672 − 7029(2021)04 − 1035 − 08

2020−06−22

国家自然科学基金资助项目(71501173)；河南省重点软科学研究项目(202400410174)；河南自贸区政策研究专项课题重点项目(2019-ZM-T06)

李玉民(1969−)，男，河南南阳人，教授，博士，从事物流与供应链管理研究；E−mail：li.yu.min@163.com

(编辑 阳丽霞)