采用干扰观测器智能PID的电磁炒药机温度控制系统设计
丁威,杜钦君,赵龙,宋传明,罗永刚,毕胜,王彬
(1.山东理工大学电气与电子工程学院,255022,山东淄博; 2.山东宏济堂制药集团股份有限公司,250100,济南)
对于需要炒制的中药饮片,温度控制的精度是反映炒制设备先进程度的重要指标,具有大惯性、时滞性以及多变量耦合的温度控制系统一直是国内外研究的难点[1-2]。温度控制的准确程度直接影响着饮片的质量、企业效益以及能源利用效率。利用蛤粉对阿胶珠炮制的温度控制精度需满足(235±5) ℃,温度过高过低都直接影响其药性及品质。传统PID控制一直被广泛应用于炒药机温度控制系统,但其控制参数KP、KI、KD不能随生产过程扰动的出现、环境因素影响以及控制对象参数发生变化而改变,且控制过程中容易出现较大的超调,无法满足阿胶珠炮制对控制精度的要求[3-4]。
采用智能控制的方法对传统PID控制参数进行动态调整,能够改善温度控制系统的动态性能,减小超调,改善系统的稳态精度。文献[5]采用BP神经网络对PID参数进行校正控制,减小了系统超调,提高了温度控制系统动态调节能力;文献[6]采用径向基函数(RBF)神经网络与PID控制相结合的方式,使温度控制系统抗干扰能力得到提高;文献[7]通过干扰观测器对控制系统进行改进,对外界干扰实现有效抑制,补偿了模型的不确定因素。
RBF神经网络具有最佳逼近性、一定的收敛能力以及良好的鲁棒性,但模型参数精度不足[8],而RBF神经网络自学习能力不足,不能快速提高模型参数的精度。因此,本文提出了一种采用改进粒子群优化(PSO)算法对RBF模型参数及神经网络突触权值进行优化,通过RBF神经网络对PID的KP、KI、KD参数进行快速动态调整的智能控制方法PSO-RBFNN-PID。在此基础上,为了降低外部环境等因素的影响,进一步提高阿胶珠炒药机温度系统运行的平稳性,引入干扰观测器,对干扰因素进行实时补偿。基于干扰观测器的PSO-RBFNN-PID控制可以有效改善RBF神经网络的学习速率、收敛能力和鲁棒性,动态调整PID控制器参数,降低外界干扰的影响,提高阿胶珠电磁炒药机温度控制系统的控制精度和响应速度。
1 炒药机温度控制系统数学模型
构建阿胶珠电磁炒药机数学模型需要考虑材料属性、热对流现象等多方面因素。本文以SYD-10Q电磁炒药机的温度控制系统为优化对象,构建炒药机温度控制系统数学模型。电磁感应加热是根据通入线圈的电流产生磁场,使电能转换为磁能,再根据涡流的热效应将其转换为被加热物体内能的过程,能量转换如图1所示。

图1 电磁感应加热能量转换Fig.1 Energy conversion of electromagnetic induction heating

图2 电磁感应加热装置物理模型Fig.2 Physical model of electromagnetic induction heating device

(1)
式中:μ为磁导率(H/m);p、u、g、o为常数。
由交变磁通φ1、φ2可得阿胶珠电磁炒药机磁动势E为
(2)
将式(2)磁动势E有效值整理为阻抗与电流相乘的形式
(3)
由式(3)可知,胶珠电磁炒药机可等效为电阻与感抗串联的形式,因此阿胶珠电磁炒药机的热功率模型可等效为[10]
(4)
式中:f为电流频率(Hz);B为磁感应强度(Wb/m2);σ为电导率(S/m);D为筒体高度(m)。在忽略磁链返回回路情况下,磁感应强度为
(5)
将式(5)代入式(4)可得
(6)
电磁感应加热的热效率可以达到95%以上。将热效率近似为1时,可以认为线圈发热量即为电磁加热的功率
(7)
式中:G为被加热物料质量(kg);C为被加热物料比热容(J/(kg·K));ΔT2为期望温度与室温之差(K);Δb为室温到期望温度T1所需时间(s);S为筒体表面积(m2);q为单位面积的热量损耗(W/m2),与温度成比例关系,q=kT2,T2为物料当前温度。
将q=kT2代入式(7),并对式(7)两端取拉氏变换,得到P(s)=GCsT2(s)+SkT2(s)。由于加热过程存在时滞性,所以加热功率与温度之间的传递函数为
(8)
式中:τ1=GC/Sk;K1=1/Sk。
为保证控制精度要求,考虑滚筒转动散失热量对期望温度的影响,由热对流原理可知
Q=γS1T5
(9)
式中:Q为散热功率(W);γ为传热系数(W/(m2·K));S1为物料散热面积(m2);T5为物料表面温度与筒体空气温度之差(K),T5=T2(1-m)。
通过提高电磁加热装置功率使温度升高,以弥补物料散热引起的温度降低
(10)
式中:Ga为空气质量(kg);C1为空气比热容(J/(kg·K));T4=T1-T2为物料散失温度。
对式(10)两端进行拉氏变换,得到γS1(1-m)T2(s)=GaC1sT4(s)+S1kT4(s)。因此,物料当前温度与散失温度之间的传递函数为
(11)
式中:K2=γ(1-m)/k;τ2=GaC1/S1k。
由此,可得阿胶珠电磁炒药机温度控制系统控制结构,如图3所示。

r(t)—系统输入;y(t)—系统输出。图3 炒药机温度控制系统控制结构Fig.3 Control structure of temperature control system of stir-frying machine
2 炒药机温度控制系统结构
传统PID控制中KP、KI、KD参数相互制衡,需要依靠经验进行设定,且不能实时动态调整[11]。若炒药机参数发生变化或产生大的干扰,需要重新进行参数设定,参数设定繁琐且很难达到最优,并且在调试过程中会造成阿胶粒的极大浪费,造成阿胶珠成品率低,降低企业的生产效益,不能满足阿胶珠批量生产的要求。
根据阿胶珠炒药机实际生产要求,为避免外部因素及模型参数影响产生的干扰,利用干扰观测器将外部干扰及模型变换产生的差异在控制过程中给予补偿,达到对干扰的有效抑制。为弥补传统PID参数不能实时调节、控制精度不足以及滞后严重的问题,应用PSO-RBFNN-PID控制,利用改进PSO算法进行RBF神经网络参数的在线调节[12],优化RBF神经网络的突触权值ω、中心向量c以及宽度参数σ,提高RBF神经网络的泛化能力、鲁棒性能以及全局收敛能力,实现对PID控制器KP、KI、KD参数进行动态调整,提高系统的控制精度以及响应速度。炒药机温度控制系统结构如图4所示。

e(t)—误差;de(t)/dt—误差变化率;u(t)—控制器输出;d(t)—干扰量;n(t)—测量噪声;d′(t)—等效干扰; u′(t)—等效补偿量;ε(t)—观测器补偿误差;Gn(s)—干扰观测器名义模型;D(s)—低通滤波器。图4 炒药机温度控制系统结构Fig.4 Temperature control system structure of stir-frying machine
2.1 PSO-RBFNN-PID控制器设计
本文的控制器由传统PID控制器和改进PSO优化RBF神经网络部分组成,如图4左半部分所示。通过对控制系统进行闭环控制,得到系统输入r(t)与输出y(t)产生的误差及其变化率,误差e(t)反映期望温度与实测温度之间的偏差,误差变化率de(t)/dt反映系统运行状态的变化趋势。通过将系统输出y(t)、误差以及误差变化率作为RBF神经网络的输入x,将系统误差瞬时值εe(t)作为改进PSO算法的适应度函数,对RBF神经网络参数进行在线优化调整,使RBF神经网络输出能够动态调整的最优KP、KI、KD参数。系统误差瞬时值表达式为
(12)
PID控制输出表达式为
(13)
根据递推原理,离散化输出的增益可表示为
Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+KD[e(k)-2e(k-1)+e(k-2)]
(14)
u(k)输出表达式为
u(k)=u(k-1)+Δu(k)
(15)
2.1.1 RBF神经网络设计 RBF神经网络是一种包括输入层、隐含层和输出层的前馈神经网络[13],引入RBF神经网络能够弥补传统炒药机PID控制需要依靠经验进行参数设定[14-15]、过程烦琐且控制精度不高的缺陷,其结构图如图5所示。

图5 RBF神经网络结构Fig.5 Structure of RBF neural network
本文隐含层节点数选取[16]为
z=2n+1
(16)
式中:z为隐含节点数;n为输入层节点数。
神经网络中BRF选取为高斯函数
(17)
式中:cj(t)表示第j个隐含节点在t时刻的中心向量;σj(t)为第j个隐含节点在t时刻的宽度参数;‖x(t)-cj(t)‖为欧氏范数,表示第i个输入向量到第j个中心向量的距离。
RBF神经网络的输出yout(t)为
(18)
式中ωjk(t)为第j个隐含节点在t时刻对于第k个输出层的突触权值。
2.1.2 PSO算法设计 粒子群算法能够优化神经网络参数,增强其学习速率、收敛能力和鲁棒性,提高炒药机温度控制系统响应速度和控制精度。在粒子群算法中,定义一组代表每个粒子的个体,每个粒子代表一组对于优化对象优化的可能解[17]。群体在多维空间每个粒子都有代表自身的矢量位置xi,j以及代表自身飞行速度的矢量vi,j,通过自我学习以及粒子间信息交流来更新自身最优位置pi,j、全局最优位置pg,j以及自身速度vi,j(t),并计算种群最优位置的适应度[18]。
标准PSO算法惯性权重w及学习因子l1、l2为常数,容易使优化算法陷入早熟或局部最优,其各粒子位置矢量和速度矢量更新公式[19]为
(19)
式中:vi,j(t)代表第t次迭代中第i个粒子在第j维的当前运动速度;xi,j(t)代表第t次迭代中第i个粒子在第j维的当前位置;b1、b2为两个互不影响的0~1的随机数;w为惯性权重;迭代中需设定最大位置xmax和最大速度vmax。
惯性权重线性递减,能够使迭代初期的全局搜索能力和迭代后期的局部搜索能力得到提高。学习因子l1、l2反映了各粒子之间的信息交流,能够加强迭代初期算法的自我学习能力和迭代后期的社会学习能力,有利于提高算法的收敛速度。w、l1、l2更新式为
(20)
(21)
式中:wmax为权重的最大值;wmin为权重的最小值;St为当前迭代步数;St,max为最大迭代步数;l1,ini、l1,fin和l2,ini、l2,fin分别为l1、l2的迭代初值和终值。
2.1.3 梯度下降法 通过改进PSO算法对RBF神经网络输出层中心向量、宽度参数、突触权值进行优化。在系统运行过程中,RBF神经网络采用梯度下降法对迭代过程中的网络参数进行适当调整,以减小炒药机温度控制误差。梯度下降法公式为
(22)
(23)
(24)
式中:cij为第j个隐含节点对于第i个输入节点的中心向量元素;η为学习率;α为动量因子。
2.2 干扰观测器设计
生产过程中,炒药机温度控制系统受环境因素、喂料速度、阿胶粒质量等多方面干扰,突变的干扰量会引起系统扰动,引起温度波动,增大输出误差,影响智能控制器动态调节PID参数过程中阿胶珠的品质。为了对突变干扰量进行迅速有效抑制,采用干扰观测器对干扰进行实时补偿。通过对外部干扰因素以及炒药机本身与被控模型的差异进行观测,使在控制过程中,观测出等量的补偿值并反馈给输入端,以实现多干扰的抑制[20]。
如图4右下部分所示,干扰观测器由被控对象G(s)的名义模型Gn(s)和低通滤波器D(s)组成[21]。结合炒药机温度控制系统结构(图4右上部分G1(s)、G2(s)),由式(8)(9)可得被控对象G(s)为
(25)
式中:τ3=τ2K1;K3=K1(1-K2);τ4=τ1τ2;τ5=τ1+τ2。
干扰观测器名义模型Gn(s)可表示为
(26)
在无测量噪声n(t)的情况下,干扰观测器中等效干扰d′(t)为
d′(t)=[ε(t)+d(t)]G(s)G-1(s)-ε(t)=d(t)
(27)
由式(27)可知,观测器可以将干扰量进行有效等效,进而对炒药机所受干扰进行补偿。但是,对于实际炒药机温度系统,被控温度G(s)为有理真分式,且准确的数学模型不易得到,在实际物理模型中不存在G-1(s),由于测量噪声的存在,控制精度也会下降。为此,在等效干扰补偿过程中引入一个低通滤波器D(s)使模型变为有理真分式。根据梅森公式,由图4可得干扰观测器传递函数为
(28)
由式(28)可知,当G(s)=Gn(s)时,在低频情况(Q(s)=1)和高频情况(Q(s)=0)下分别有
(29)
Gny(s)=0
(30)
由式(29)(30)可以看出,若名义模型即为被控对象模型,则有以下结论:①PSO-RBFNN-PID控制器输出u(t)与炒药机输出y(t)之间的传递函数没有因为干扰观测器的引入而改变,干扰观测器没有参与智能控制器对炒药机的温度控制;②干扰观测器能够对干扰进行有效补偿;③干扰观测器能够滤除高频噪声。
由于延迟环节e-τs的延迟因子为不确定部分,采用积乘积摄动对炒药机模型进行描述
G(s)=Gn(s)[1+Δ(s)]
(31)
式中Δ(s)=e-τs-1为高频振动。
在设计干扰观测器时,保证鲁棒稳定性的充分必要条件为
(32)
式中:D(s)为3阶低通滤波器状态空间表达式;Δ为高频振动状态空间表达式。
因此,在实际运行过程中,为了保证引入干扰观测器的炒药机控制系统稳定性和低通性能[22],采用3阶低通滤波器作为D(s),公式为
(33)
式中ζ为时间常数。
3 温度控制参数优化步骤
改进PSO算法优化RBF神经网络PID控制器如图4左半部所示,RBF采用式(18)所示的高斯函数。控制过程主要包括3部分:①改进PSO算法对RBF神经网络中心向量、宽度参数以及突触权值进行优化更新;②RBF神经网络输入信号分别为系统的输出y(t)、系统误差e(t)以及误差变化率de(t)/dt,以RBF神经网络输出信号yout作为PID控制器输入参数,对控制器参数进行动态调整;③通过PID控制器输出量u(t)对阿胶珠电磁炒药机温度进行控制。控制过程具体步骤如下。
步骤1初始化粒子数、迭代数、各粒子位置矢量、各粒子速度矢量、粒子群参数(w、l1、l2、xmax、vmax)、神经网络参数。
步骤2根据图3所示的温度控制系统,计算系统y(t)、e(t)、de(t)/dt,进行归一化处理,赋值给RBF神经网络输入层节点x。
步骤3根据式(18)计算RBF神经网络输出参数,对PID控制器参数KP、KI、KD赋值。
步骤4根据PID参数KP、KI、KD,通过式(15)计算得到PID控制输出u(t),并根据期望值对输出u(t)幅值进行限制以加快响应速度。
步骤5各粒子开始进行迭代,将中心向量、宽度参数以及突触权值作为粒子寻优目标,其中一个粒子代表一个49维的解,算法的适应度函数用式(12)所示的温度控制系统误差瞬时值表示。
步骤6将每个粒子的位置信息分别映射给RBF神经网络,通过式(12)计算每个粒子的适应度。
步骤7将每个粒子当前位置和前一位置适应度作比较,若当前位置适应度优于前者,则将当前位置作为粒子的最优位置pi,j。将每个粒子最优位置适应度与全局最优位置适应度比较,适应度最优者的位置为全局最优位置pg,j。
步骤8更新每个粒子最优位置pi,j和全局最优位置pg,j。根据式(19)更新每个粒子的位置矢量和速度矢量。
步骤9若迭代过程适应度函数值为0或达到最大迭代数,迭代终止,将全局最优位置的粒子映射给RBF神经网络的优化参数,根据式(22)~(24)对RBF神经网络参数ω、c和σ进行适当调整,得到RBF神经网络最优输出参数KP、KI、KD;否则根据图4重复步骤2~9。
步骤10记录每次迭代最优位置适应度。
根据优化步骤,式(19)的标准PSO算法和式(19)~(21)的改进PSO算法的适应度变化曲线如图6所示。可以看出:标准PSO算法惯性权重和学习因子为常值,迭代初期收敛速度过快,并且在第42次迭代以后陷入局部最优;改进PSO算法各参数随迭代数不断更新,加强了各粒子间的信息交流,避免了陷入早熟或局部最优。
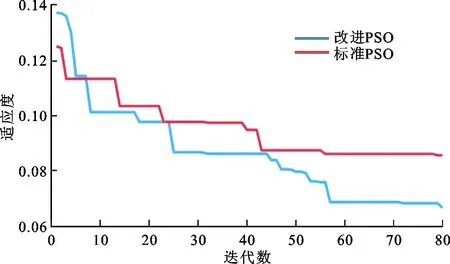
图6 适应度变化曲线Fig.6 Fitness curves
4 仿真分析
结合炒药机实际设备参数及控制经验,根据式(25)所示的传递函数,对炒药机系统数学模型进行参数求解,得到:τ=10,τ3=800,K3=45,τ4=1 280,τ5=96。
由式(29)(30)可以看出,干扰观测器没有参与智能控制器对炒药机的温度控制,只对干扰量进行抑制。为了切合实际生产,考虑多方面干扰因素的影响,更加直观地反映干扰观测器的性能,首先在仅考虑干扰观测器的情况下,对炒药机温度控制系统进行仿真实验,即仅对输入为u(t)至输出y(t)进行仿真。仿真实验取预热时间为80 s,阿胶珠炒制温度为235 ℃,预热完成后炒药机进料炒制,施加±1的干扰量,仿真结果如图7所示。

图7 基于干扰观测器的温度系统仿真Fig.7 Temperature system simulation based on disturbance observer
从图7可以看出:引入干扰观测器能够提高系统的鲁棒性,抑制干扰对温度波动的影响;相较于无干扰观测器,引入干扰观测器对外部干扰抑制能力平均提高50%,但干扰观测器不能改善控制系统的响应速度和动态调节能力,因此采用PSO-RBFNN-PID控制器来提高炒药机温度控制系统的性能指标。
改进PSO算法参数如下:wmax=0.9,wmin=0.4;l1,ini=l2,fin=2.5,l1,fin=l2,ini=0.5;迭代数为50;xmax=vmax=±5;PID控制限制输出u(t)幅值为240;RBF神经网络初始参数η=0.5,α=0.05;在区间[-1,1]随机初始化中心向量、位置参数以及突触权值,取输入输出节点数均为3,根据式(16)计算隐含层节点数为7。
为了验证控制器性能,分别采用传统PID控制、RBFNN-PID控制和改进PSO-RBFNN-PID控制,以单位阶跃响应为系统输入,对式(25)的阿胶珠电磁炒药机模型进行控制,对温度控制系统在无扰动和在3 s增加幅值为0.1的扰动情况下进行闭环控制仿真验证。
阿胶珠电磁炒药机温度控制系统正常运行状态下,电磁炒药机温度系统输出y(t)、PID控制器输出u(t)以及系统误差e(t)如图8~10所示。

图8 温度控制系统输出曲线Fig.8 Output curves of temperature control system
根据图4以及图8计算得到各控制方式的温度控制系统动态性能指标,如表1所示。

表1 温度控制系统动态性能

图9 PID控制器输出曲线Fig.9 Output curves of PID controller

图10 温度控制系统误差曲线Fig.10 Temperature control system error curves
根据图8~10以及表1可以看出:由于传统PID控制参数是靠经验事先设定的定值,RBF神经网络初始值随机给定,需要一定的学习时间,因此传统PID和RBFNN-PID方法会出现较大超调,且调节时间较长,不能满足阿胶珠炮制对温度控制的要求;引入PSO算法的控制方法通过算法的寻优能力改善神经网络参数,赋予神经网络更强的学习能力,能在更短时间内使阿胶珠电磁炒药机温度到达稳态值且超调量很小。
为验证PSO-RBFNN-PID方法在受干扰情况下的动态性能,在3 s时,对系统加入0.1幅值的扰动量,此时电磁炒药机温度系统输出y(t)、PID控制器输出u(t)以及系统误差e(t)曲线如图11~13所示。

图11 有扰动系统输出曲线Fig.11 Output curves of perturbed system

图12 有扰动PID控制器输出曲线Fig.12 Output curves of PID controller with disturbance

图13 有扰动系统误差曲线Fig.13 The error curves of disturbance system
根据图11~13可以看出,阿胶珠电磁炒药机温度系统产生扰动后,PSO-RBFNN-PID方法能够在短时间内优化RBF神经网络各项参数,提高RBF神经网络的收敛速度和逼近能力,使RBF神经网络输出的最优PID参数。由图11可以看出,PSO-RBFNN-PID方法输出u(t)响应速度最快,调节能力最强,能够使炒药机温度控制系统在短时间回到稳态运行状态。综上可知,PSO-RBFNN-PID方法最优。
5 结 论
为了提高电磁炒药机温度控制系统性能,满足阿胶珠炮制对温度的要求,本文提出了一种基于干扰观测器的改进粒子群优化RBF神经网络PID的控制方法,使温度控制精度和响应速度得到提高。本文主要结论如下。
(1)以SYD-10Q电磁炒药机为控制对象,考虑设备自身结构参数及热对流影响,构建了电磁炒药机温度控制系统数学模型。
(2)根据控制系统结构,构建了输入节点数为3、隐含节点数为7、输出节点数为3的RBF神经网络,以给定温度与输出的误差瞬时值作为改进粒子群算法的适应度函数,实现了对RBF神经网络模型参数寻优,使RBF神经网络对PID参数动态调节精度得到改善。在此基础上,通过构建干扰观测器,提高了系统对外界干扰的抑制能力。
(3)将本文控制方法与传统PID控制方法和RBFNN-PID控制方法进行了仿真实验比较,结果表明:本文控制方法比另两种方法调节时间分别减少了35 s和19 s,超调量分别降低了19.2%和13.1%,具有更强的动态调节能力;干扰观测器的引入使对外部干扰抑制能力平均提高50%,系统稳态精度得到改善。
本文提出的控制方法对其他饮片炮制设备的温度控制应具有一定的参考价值。由于神经网络模型参数较多,优化过程较为烦琐,未来可对神经网络模型参数选取做进一步探究。

