采用Bulk-Flow模型的直通式迷宫密封转子动力特性研究
王天昊,李志刚,李军
(西安交通大学叶轮机械研究所,710049,西安)
迷宫密封结构简单、技术成熟、制造维护成本低廉,因此被广泛应用于透平机械中来控制动静间隙的泄漏流动,从而降低泄漏损失和泄漏流对主流的影响。然而,迷宫密封在有效控制泄漏流动的同时会产生显著的流体激振力,严重威胁转子系统的安全稳定运行[1]。迷宫密封转子动力特性受到诸多因素的影响,例如密封几何结构、进出口压力、预旋比和转子转速等。因此,根据几何结构和运行工况参数快速准确预测迷宫密封转子动力特性系数,对于设计制造先进透平机械装置具有重要的工程应用价值。
目前,主要采用Bulk-Flow模型[2]和三维数值方法来预测迷宫密封的转子动力特性系数。其中,三维数值方法中的多频椭圆涡动模型[3]具有计算效率和精度方面的优势,常被用于密封转子动力特性精细化分析。与基于动网格技术和非定常方法的多频椭圆涡动模型相比,Bulk-Flow模型具有预测速度快、对计算资源要求低且预测结果能满足工程分析精度的优点,至今仍是工业界应用最广泛的密封动态特性预测模型。
在Iwatsubo提出的单控制体等温Bulk-Flow模型[2]的基础上,Childs等考虑了转子偏心引起的密封腔室周向截面面积的变化,来预测直通式迷宫密封的转子动力特性[4]。该模型假设泄漏流为理想气体,泄漏流动过程为等温过程,且不考虑转子转动的影响。通过与当时有限的实验数据对照,Childs等的模型对无量纲交叉刚度的预测误差在25%以内[4]。Scharrer改进了适用于直通式迷宫密封的双控制体Bulk-Flow模型,率先在控制方程组中考虑了密封腔室内涡流速度的影响,与Childs的单控制体模型相比,提高了对交叉刚度和直接阻尼的预测精度[5]。然而,Picardo和Childs通过将两种模型的预测结果与高压实验结果比较发现,单控制体模型相比于双控制体模型总体预测精度更高[6]。
近年来,晏鑫等发展了双控制体Bulk-Flow模型来预测孔型密封的转子动力特性[7]。袁振伟等采用单控制体Bulk-Flow模型研究了液相环形密封的转子动力特性和密封进口涡动系数对轴系稳定性的影响[8]。席文奎等采用双控制体Bulk-Flow模型研究了迷宫密封对高参数汽轮机转子系统稳定性的影响[9]。Cangioli等在单控制体Bulk-Flow模型的控制方程中引入了能量方程,通过假设泄漏流动过程为绝热过程来考虑密封腔室之间泄漏流焓变的影响,并在提取密封转子动力特性系数时考虑了涡动频率相关性,提高了Bulk-Flow模型对负预旋工况下迷宫密封转子动力特性的预测精度[10]。
尽管Bulk-Flow模型具有预测速度快的优点,但是该模型忽略了流场的精细结构,预测精度显著依赖所选用的半经验泄漏模型。泄漏模型是基于理论分析或实验结果的单密封齿处泄漏量预测公式,以泄漏方程为基础,并引入两个修正系数。目前,常用的两种泄漏方程是St.Venant方程[11]和Neumann方程[12]。流量系数和动能输运系数分别被用于修正流体通过密封间隙时流束收缩效应和透气效应对密封泄漏量的影响[13]。此外,摩擦系数模型的选取对切应力的计算有重要影响,进而影响到密封转子动力特性预测的准确性[14]。
目前,由于泄漏模型适用性研究很少且不全面,在使用Bulk-Flow模型预测迷宫密封转子动力特性时,存在泄漏模型选择的困难。本文基于单控制体等熵过程Bulk-Flow模型发展了直通式迷宫密封转子动力特性预测方法并开发了计算程序。通过与Vannini等的实验数据[15-16]比较,对不同经验公式组合成的72种泄漏模型进行适用性分析,获得了最佳泄漏模型,并在预测程序中采用该模型研究了压比和预旋比对直通式迷宫密封转子动力特性的影响规律。
1 计算模型与数值预测方法
1.1 控制方程
图1给出了直通式迷宫密封子午面几何结构和控制体示意图。
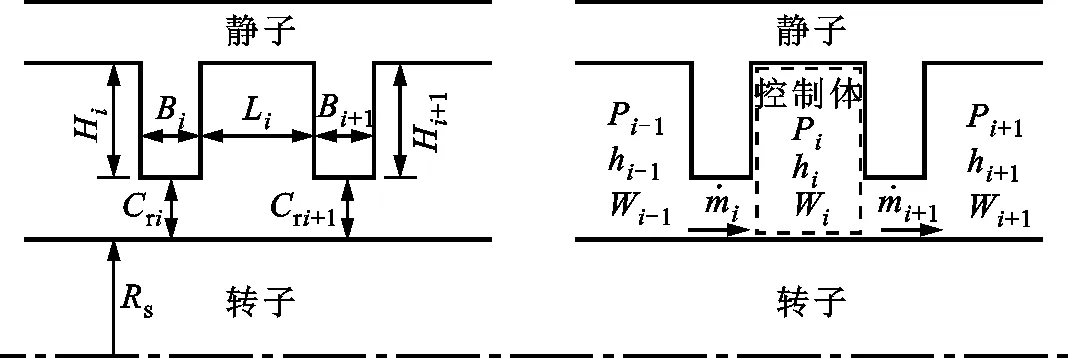
(a)子午面几何结构 (b)子午面控制体 Rs—密封半径;Cr—密封间隙;H—密封齿高度;B—密封齿厚度; L—密封腔室长度;P、h、W—控制体的压力、比焓和周向旋流速度; 密封间隙处的单位周向长度泄漏流率; 下标i—密封齿或密封腔室序号。图1 迷宫密封子午面几何结构和控制体示意图Fig.1 Schematic diagram of geometry and control volume of the labyrinth seal in meridian plane
本文采用的数值预测方法基于Cangioli等的单控制体Bulk-Flow模型[10],假设泄漏流动过程为等熵过程,计算中采用实际气体性质,考虑转子动力特性系数的频率相关性。忽略密封腔室内流体参数在轴向和径向的变化,推导如图2所示控制体的控制方程,包括连续方程、周向动量方程和能量方程
(1)
(2)
(3)
式中:ρ是流体密度;A是控制体周向截面面积;τr和τs分别是转子面和静子面作用于控制体的切应力;ar和as分别是转子面和静子面的无量纲长度;u是控制体比内能;ω是转子转动角速度。
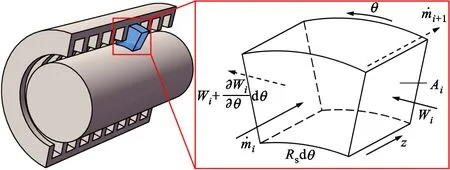
图2 单控制体模型示意图Fig.2 Schematic diagram of one-control-volume model
1.2 摄动分析
为了求解上述非线性多元偏微分方程组,采用摄动分析方法将方程组线性化。如图3所示,假设转子轴心绕静子中心沿椭圆轨迹涡动,但不考虑转子涡动引起的焓变,即只在零阶稳态方程中考虑能量方程。以ε为摄动参数,引入以下摄动变量
(4)
式中:下标0表示变量的零阶稳态值;下标1表示变量的一阶摄动函数。由于流体比焓hi不受转子涡动的影响,故忽略比焓摄动项。
将上述摄动变量代入控制方程中,可以得到零阶稳态方程和一阶摄动方程。零阶稳态方程决定了转子在中心时的泄漏流率以及密封腔室内的稳态压力、周向旋流速度和比焓,可以使用多元牛顿迭代法求解。一阶摄动方程是描述转子涡动时密封腔室的压力摄动项、周向旋流速度摄动项和密封间隙摄动项之间关系的空间二维非稳态方程组,需要采用如下变换进行求解。
如图3所示,转子轴心涡动轨迹可表示为
x=εacosΩt;y=εbsinΩt
(5)
式中:εa和εb分别是椭圆涡动轨迹的长半轴和短半轴长度;Ω是转子涡动角速度。
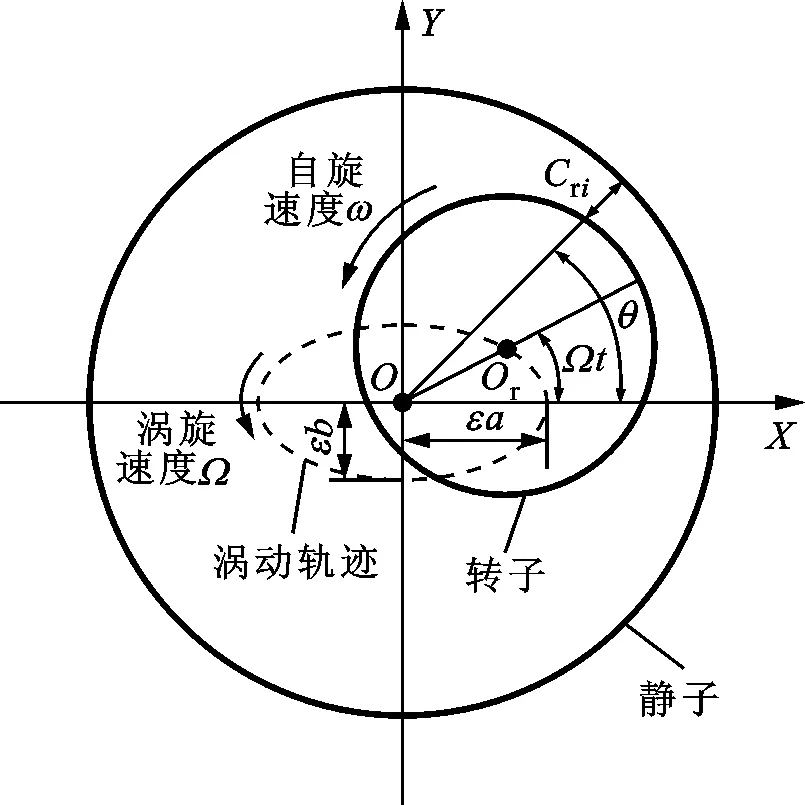
图3 椭圆轨道转子涡动模型Fig.3 Elliptical-orbit rotor whirling model
根据转子运动规律,密封间隙摄动函数可表示为复数形式
Cr1(t,θ)=-acosΩtcosθ-bsinΩtsinθ=
(6)
式中:j为虚数单位。
因此,密封腔室压力和周向旋流速度的摄动函数可以表示为相似的形式
(7)
(8)
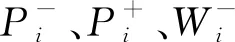
将式(6)(7)(8)代入一阶摄动方程得到复变量线性方程组
(9)

对于具有N个密封齿的迷宫密封,联立N-1个密封腔室的一阶摄动方程,得到4(N-1)阶复变量线性方程组。利用LU分解方法求解上述方程组,并将结果代入式(7)(8)可以得到密封腔室压力和周向旋流速度的摄动函数。
1.3 转子动力特性系数的提取
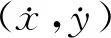
(10)
式中K、k、C、c分别为直接刚度、交叉刚度、直接阻尼和交叉阻尼。
将式(5)代入上式并写作复数形式
F=Fx+jFy=
(11)
作用于转子的流体激振力F还可以通过压力摄动函数和表面切应力沿周向积分得到
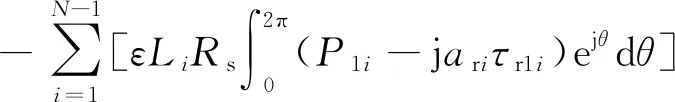
(12)
式中τr1i为作用于转子表面的切应力摄动量。
将压力摄动函数P1i和切应力摄动量τr1i的表达式代入上式并整理得
(13)
式中Z-和Z+是由复变量方程(9)的解决定的复常量。
比较式(11)和(13),得到密封转子动力特性系数
(14)
2 泄漏模型适用性分析
半经验的泄漏模型对Bulk-Flow模型的预测精度有决定性的影响。本文采用Vannini等的14齿直通式迷宫密封转子动力特性实验结果[15-16]作为验证算例,对72种泄漏模型进行适用性分析。本文只评价泄漏模型对迷宫密封交叉刚度和直接阻尼的预测精度,这是因为由直接刚度和交叉阻尼决定的密封有效刚度比轴承有效刚度低一个数量级以上[10],与之相比,交叉刚度和直接阻尼对转子振动稳定性的影响更为显著。
本文研究的72种泄漏模型由2种泄漏方程、3种流量系数、6种动能输运系数和2种切应力系数组合而成[18]。泄漏方程包括St.Venant和Neumann泄漏方程,并改写为适用于实际气体的形式;流量系数包括Chaplygin和Eser & Kazakia流量系数,还研究了不对流束收缩效应进行修正的None系数(该系数取1.0);动能输运系数包括Neumann、Hodkinson、Hodkinson-M、Vermes和Kurohashi动能输运系数,同样考虑了不修正透气效应的None系数;切应力系数包括Swamee & Jain和Blasius切应力系数,前者考虑了密封表面粗糙度的影响。
对于不同泄漏模型,采用本文开发的迷宫密封转子动力特性预测程序计算6个算例下的密封交叉刚度和直接阻尼,并与实验结果[15-16]进行对比。表1和表2分别给出了实验采用的迷宫密封几何参数和6个算例对应的运行工况参数,每个算例都包括5种涡动频率的工况,工质为氮气。
为了评价不同泄漏模型关联式的预测精度,图4给出了以关联式分类的平均预测误差,定义为采用某一关联式的所有泄漏模型对各个工况下交叉刚度和直接阻尼预测的平均相对误差。如图4所示:Neumann泄漏方程平均预测误差比St.Venant泄漏方程低3.6%;考虑流束收缩效应影响的两种流量系数平均预测误差几乎相等,且远低于不考虑修正的None关联式;动能输运系数的选择对模型预测精度影响显著,Hodkinson-M动能输运系数平均预测误差最小,不考虑透气效应修正的None关联式平均预测误差远高于其他关联式;两种切应力系数表现相似,考虑表面粗糙度影响的Swamee & Jain切应力系数平均预测误差稍低于Blasius切应力系数。综合以上分析,预测精度较高的泄漏模型应对流束收缩效应和透气效应进行修正,应采用Swamee & Jain切应力系数来根据表面粗糙度准确计算转子表面切应力。
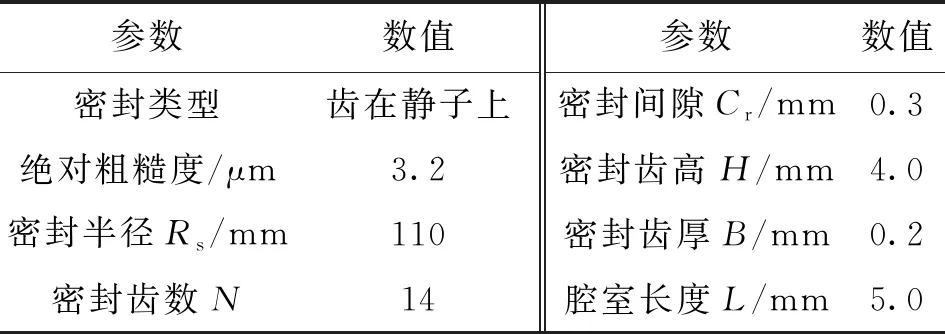
表1 迷宫密封几何参数

表2 运行工况参数
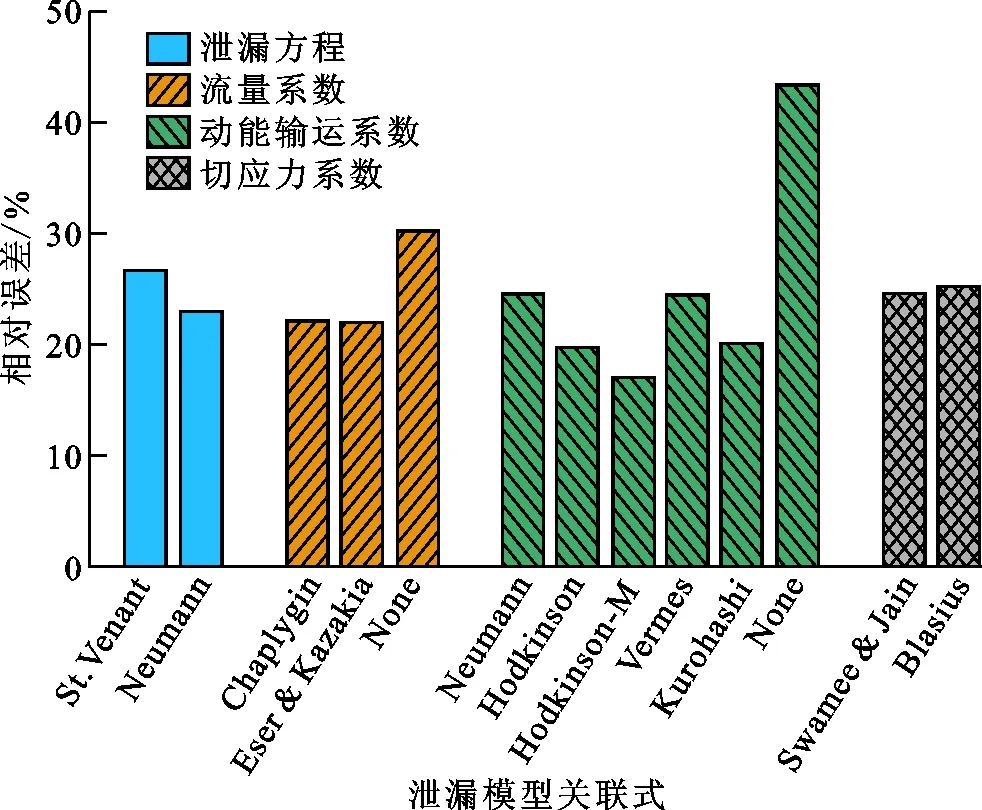
图4 以关联式分类的平均预测误差Fig.4 Average prediction error for a specific correlation
为了进一步对符合上述要求的20种泄漏模型进行评价,图5给出了不同泄漏模型的平均预测误差。如图5所示:采用Vermes动能输运系数的泄漏模型预测精度最低,平均预测误差均接近或超过20%,在下面的讨论中不再考虑;剩余的泄漏模型中,采用Eser & Kazakia常量流量系数配合Neumann泄漏方程的泄漏模型预测精度高于配合St.Venant泄漏方程的泄漏模型,其平均预测误差均略高于10%;采用Chaplygin流量系数的泄漏模型预测精度受泄漏方程和动能输运系数的影响显著,表3中给出了平均预测误差低于10%的3种泄漏模型,共同点是采用了Chaplygin流量系数。
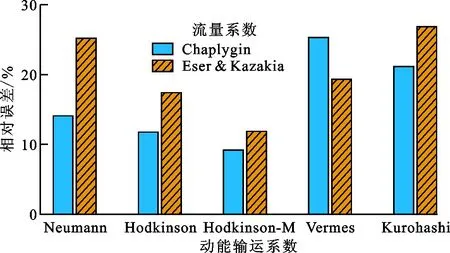
(a)St.Venant泄漏方程

(b)Neumann泄漏方程图5 不同泄漏模型的平均预测误差比较Fig.5 Comparison of average prediction errors of different leakage models
泄漏模型适用性受迷宫密封运行工况的影响较大。图6给出了采用上述3种泄漏模型时,在不同预旋方向和进出口压差工况下迷宫密封交叉刚度k和直接阻尼C随涡动频率f的变化,并与实验值的比较。如图所示:总体上,3种泄漏模型都正确反映了k和C随f的变化趋势;正预旋工况下,Mod 3预测误差最小,在多数工况下的预测误差在测量不确定度范围内;Mod 1对负预旋低压降工况的预测结果与实验曲线符合较好,但低估了高压降工况下的交叉刚度;Mod 2计算获得的交叉刚度在负预旋高压降工况与实验值吻合良好,但在低压降工况的高频区(f>120 Hz)比实验值偏高,且普遍低估了负预旋工况下的直接阻尼。根据转子动力学理论:交叉刚度越小,直接阻尼越大,系统越稳定。从冗余设计的角度出发,在负预旋工况下应采用Mod 2来预测迷宫密封转子动力特性,以保证转子系统具有足够的振动稳定性。

表3 平均预测误差低于10%的泄漏模型

(a)算例2(正预旋,高压降)
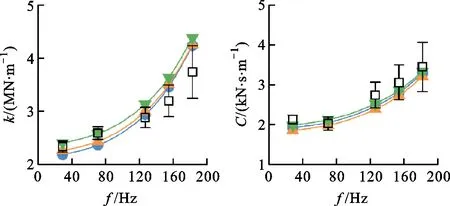
(b)算例4(正预旋,低压降)
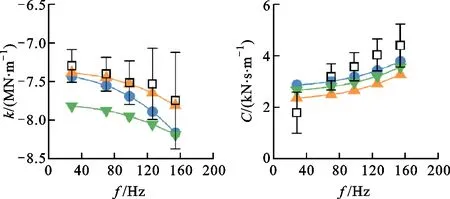
(c)算例5(负预旋,高压降)

(d)算例6(负预旋,低压降)图6 不同泄漏模型下迷宫密封交叉刚度和直接阻尼随 涡动频率的变化Fig.6 Cross-coupled stiffness and direct damping versus vibration frequency for different leakage models
综合以上分析,最佳泄漏模型选择方案是正预旋工况下采用Mod 3而负预旋工况下采用Mod 2,这样可以获得准确且保守的迷宫密封交叉刚度和直接阻尼预测结果,平均预测误差约为10%。
3 转子动力特性影响因素研究
为了研究运行工况参数对直通式迷宫密封转子动力特性的影响,在Bulk-Flow模型预测程序中采用上述最佳泄漏模型,计算了表1所示的迷宫密封在不同工况下的交叉刚度和直接阻尼。为了更加直观地表现迷宫密封对转子系统稳定性的影响,计算了密封有效阻尼,公式为
(15)
3.1 压比的影响
压比π定义为密封出口压力Pout与进口压力Pin之比。为了研究压比对直通式迷宫密封转子动力特性的影响,计算了迷宫密封在3种压比(π=0.3,0.5,0.7)下的转子动力特性系数,以Pin=7.250 MPa、Pout=5.075 MPa为基准工况,通过减小Pout或增大Pin来改变压比。计算采用的预旋比λ=0.4,转子转速n=10 000 r/min。
图7和图8分别给出了Pout变化和Pin变化时,不同压比下迷宫密封转子动力特性系数随涡动频率的变化。如图7和图8所示:交叉刚度和直接阻尼均随涡动频率增大而增大,且在高频区的频率相关性更为显著;有效阻尼的穿越频率fc几乎不受密封进出口压力的影响,在各个工况下均为72 Hz左右;当f>fc时,Ceff随f增大而近似线性增大。对于图7所示Pin不变的情况,Pout的变化对k和C的影响很小;在图8所示Pout不变的情况下,k、C和Ceff的绝对值均随Pin增大而增大。
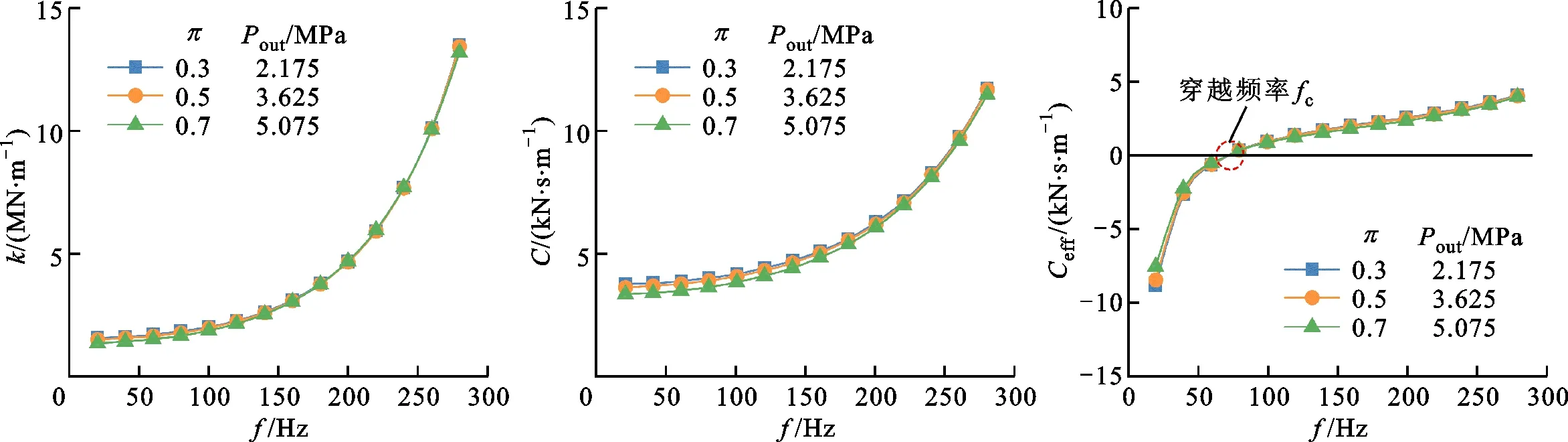
图7 不同压比下迷宫密封转子动力特性系数随涡动频率的变化(Pin=7.250 MPa,Pout变化)Fig.7 Rotordynamic coefficients versus vibration frequency at different pressure ratios (Pin=7.250 MPa with different Pout)
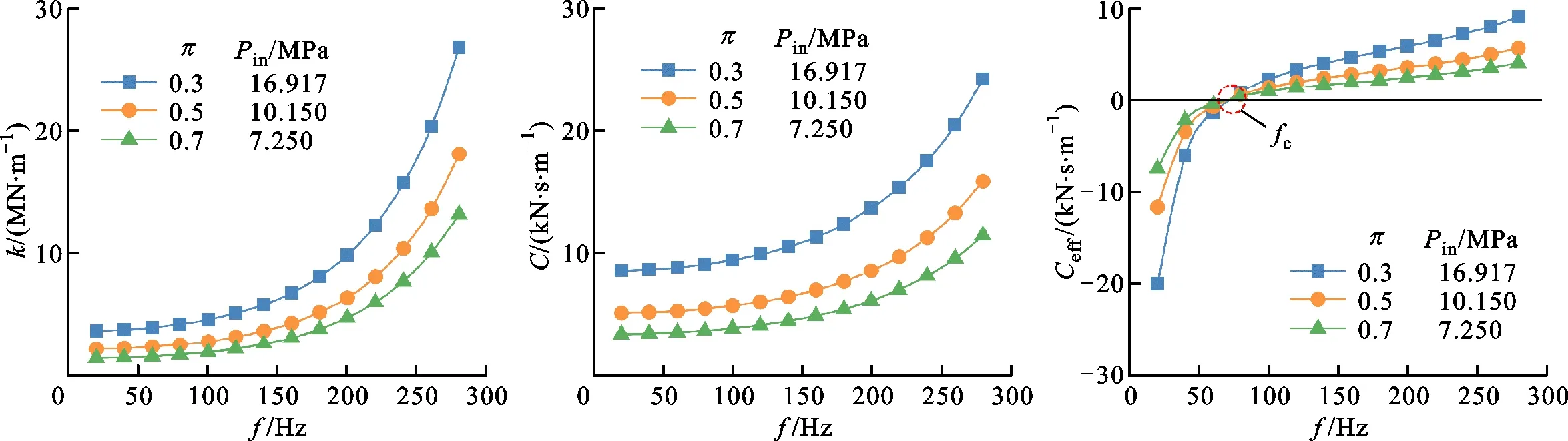
图8 不同压比下迷宫密封转子动力特性系数随涡动频率的变化(Pin变化,Pout=5.075 MPa)Fig.8 Rotordynamic coefficients versus vibration frequency at different pressure ratios (Pout=5.075 MPa with different Pin)

图9 不同进出口压力下迷宫密封各腔室压力沿流动方向的分布Fig.9 Distribution of cavity static pressure along flow direction at different supply and discharge pressure
以上研究表明:迷宫密封交叉刚度和直接阻尼对密封进口压力敏感,而受出口压力的影响有限。这是因为在不同进出口压力工况下,密封各腔室压力沿流动方向分布不同。如图9所示:Pout不变而Pin变化时,各个腔室压力均随Pin增大而增大,上游腔室的压力变化更为显著;Pin不变而Pout变化时,各个腔室压力均随Pout降低而降低,但变化幅度均远小于相同压比下Pin变化的情况,且达到临界工况后,密封各腔室压力不再变化。因此,迷宫密封各腔室压力分布对进口压力的变化更加敏感,这与密封转子动力特性系数受进口压力的影响更加显著的现象相一致。
3.2 预旋比的影响
预旋比λ定义为密封进口预旋速度Win与转子表面线速度之比
(16)
式中:R是转子半径;n是转子转速。
为了研究预旋比对直通式迷宫密封转子动力特性的影响,计算了迷宫密封在5种预旋比(λ=-0.8,-0.4,0,0.4,0.8)下的转子动力特性系数。计算采用的Pin=7.250 MPa,Pout=5.075 MPa,n=10 000 r/min。

图10 不同预旋比下迷宫密封转子动力特性系数随涡动频率的变化Fig.10 Rotordynamic coefficients versus vibration frequency at different preswirl ratios
图10给出了不同预旋比下迷宫密封转子动力特性系数随涡动频率的变化。如图10所示:尽管迷宫密封在整个涡动频率范围内均具有正的直接阻尼,且C随λ增大而增大,但Ceff仍随λ增大而减小,特别是在低频区内降幅十分显著,这是由交叉刚度的变化导致的;k随λ增大而增大,且在高频区的增长更为明显,在λ=0附近k由负值逐渐转变为正值,这使得密封有效阻尼显著减小,不利于转子系统的稳定性。在零预旋和负预旋工况下,Ceff恒为正值,且随f增大而减小,在f>120 Hz时近似与涡动频率无关;在正预旋工况下,Ceff出现负值,随着λ增大,fc由λ=0.4时的75 Hz增大到了λ=0.8时的200 Hz,显著降低了转子系统稳定工作的涡动频率范围。
预旋比的变化改变了迷宫密封各腔室内的周向旋流速度,进而影响到密封的转子动力特性。图11给出了不同预旋比下迷宫密封腔室内周向旋流速度沿流动方向的分布。从图中可以发现,各个预旋比下密封腔室内周向旋流速度在进口处都接近进口预旋速度,而在出口附近都趋近于同一定值。因此,进口预旋速度的影响在密封上游腔室更加显著,防旋流装置应尽量安装在迷宫密封进口区域。
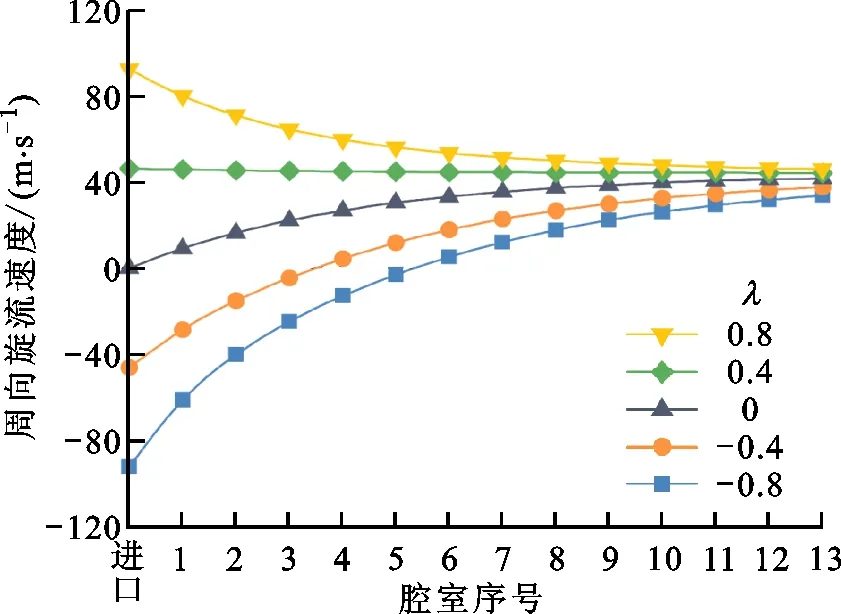
图11 不同预旋比下迷宫密封腔室内周向旋流速度沿 流动方向的分布Fig.11 Distribution of cavity circumferential velocity along flow direction at different preswirl ratios
综合以上分析,迷宫密封进口正预旋是限制密封阻尼性能和缩小转子稳定工作频率范围的关键因素,在实际工程应用中应尽量在密封进口区域采用防旋板或反向射流技术来抑制泄漏流的周向流动,从而提高转子系统的稳定性。然而,从迷宫密封传热特性角度出发,降低密封进口正预旋或提高负预旋会导致泄漏流温升增大,削弱冷却流的冷却质量[19]。为了保证转子系统的稳定运行和对热端部件的冷却效果,必须综合考虑密封的转子动力特性和传热特性来确定最佳的进口预旋。
4 结 论
本文基于单控制体等熵过程Bulk-Flow模型发展了直通式迷宫密封转子动力特性预测方法,并开发了计算程序。通过对72种泄漏模型进行适用性分析,给出了最佳泄漏模型。采用所发展的预测方法和计算程序研究了压比和预旋比对迷宫密封转子动力特性的影响规律。
(1)最佳泄漏模型是采用Neumann泄漏方程、Chaplygin流量系数、Swamee & Jain切应力系数、Kurohashi(正预旋工况)或Neumann(负预旋工况)动能输运系数的模型,该模型对直通式迷宫密封交叉刚度和直接阻尼的平均预测误差约为10%。
(2)迷宫密封交叉刚度和直接阻尼对密封进口压力敏感,而受出口压力的影响有限;密封有效阻尼的绝对值随进口压力增大而增大,其穿越频率几乎不受进出口压力的影响。
(3)预旋比是决定迷宫密封转子动力特性的关键因素。迷宫密封有效阻尼随预旋比增大而减小,在正预旋工况下出现负的有效阻尼,且穿越频率随预旋比增大而显著增大;进口预旋速度对密封上游腔室的影响更加明显。因此,进口正预旋会降低迷宫密封阻尼性能并缩小转子稳定工作的频率范围,应尽量在密封进口区域采用防旋板或反向射流技术来抑制泄漏流的周向流动。

