姿轨控发动机常平架轴承孔铣加工误差分析

张晓峰 李旭光 刘 俊

姿轨控发动机常平架轴承孔铣加工误差分析

张晓峰 李旭光 刘 俊

（西安航天发动机有限公司，西安 710100）

针对姿轨控发动机常平架正交孔系垂直度要求高，加工难以保证的问题，基于齐次坐标变换方法，建立了五轴加工中心调头加工常平架轴承孔的垂直度误差模型。结合MATLAB计算软件，对常平架的垂直度误差进行了定量分析，实现了常平架垂直度误差影响因素的预测。针对模型设计加工试验，试验结果表明，理论计算和实际加工具有较好的一致性，该方法对常平架加工误差的控制具有一定指导作用。

常平架；轴承孔；垂直度；齐次坐标变换；误差模型

1 引言

常平架是液体火箭发动机实现摇摆，达到对推力矢量进行方向控制，获得导弹或火箭控制力的关键部件[1]。某型号双向摇摆发动机所用的常平架为方环形结构，其两对轴承孔呈正交布置。为实现推力矢量精确控制，两对轴承孔轴线，即摆动轴线垂直度要求为0.05。常平架的轴线通常被选作发动机总体布局和装配的基准，其他摇摆环节也以它为基准进行布置[1]，若两个摆动方向轴线垂直度超差，传递的推力矢量会产生偏差，积累到推力室喷口位置的推力矢量误差会更大，直接影响整个发动机的姿态控制。因此对常平架轴承孔垂直度误差模型展开深入研究，以进一步提高常平架加工精度和批次一致性至关重要。

2 工艺难点分析

图1 常平架结构图

常平架的两对轴承孔分别为一对方孔和一对圆孔，如图1所示，两对轴承孔轴线垂直度要求为0.05。方孔由线切割加工，圆孔在加工中心上铣加工。由于方孔和圆孔分两次装夹加工而成，且零件外形大，轴线距离较长：两方孔间距离220mm，两圆孔间距离180mm，导致研制过程中出现垂直度0.05难以保证的难题。加工误差为多体系统问题，前期已对装夹方式和找正方法进行过多次优化，研究机床精度对常平架垂直度的影响。误差防止是常用的提高机床加工精度的方式[2，3]，通常加工误差建模方式为基于齐次坐标变换和多体系统理论的误差建模[4，5]。本文的垂直度误差模型采用齐次坐标变换的建模方法，建立常平架正交孔系垂直度误差模型，对垂直度误差进行定量分析，并分析机床转台误差对垂直度误差的影响。

3 基于齐次坐标变换的垂直度误差模型

3.1 加工中心转台误差分析

常平架的一对方孔和一对圆孔在四方形框架上成正交分布。′-′方向的一对方孔受工艺条件限制，由线切割加工而成。随后在转台式五轴加工中心上利用专用夹具装夹，借助专用工装找正方孔轴线，转台转90°对第一个圆孔铣加工，随后转180°对第二个圆孔铣加工。由加工过程可知，转台误差是常平架垂直度加工误差的最主要因素，分析转台误差对常平架正交孔系垂直度误差影响。

在转台-摆头式五轴加工中心加工圆孔时，机床主轴轴翻转至与待加工孔轴线平行，机床的加工坐标系转换如图2a所示。转台运动副存在6个自由度的运动误差，如图2b所示，理想运动是从点转到点，但由于转台误差实际运动到了点，这一过程产生6个误差分量：方向线性误差Δ、方向线性误差Δ、方向线性误差Δ、绕轴角度误差Δ、绕轴角度误差Δ、绕轴角度误差Δ。

图2 机床坐标系及转台误差示意图

3.2 基于齐次坐标变换的加工误差建模

齐次坐标变换可以用来分析空间矢量在不同坐标系间的变换问题。转台绕轴旋转时，齐次变换矩阵为[6，7]：

图2b中，从(1,1,1)点绕轴旋转到(2,2,2)，但由于转台运动误差实际到了(3,3,3)，考虑转台的三个位移误差Δ、Δ、Δ和三个角误差Δ、Δ、Δ引起的综合变换矩阵，实际空间运动矩阵为：

由式（2）可进一步推导出从(1,1,1)点绕轴旋转后实际点(3,3,3)与点的关系为：

3.3 常平架垂直度误差模型

常平架铣加工圆孔加工过程如图3所示。常平架加工圆孔时以方孔轴线为基准。在方孔中穿入专用工装方轴以找正基准轴线′-′，方轴和方孔采用过渡配合。为最大限度提高找正准确性，采用消除方轴和方孔间隙的办法，用柔性介质橡皮泥从一端固定方轴。出于这一过程操作方便考虑，初始装夹位置如图3a所示，方轴大致平行于轴。

图3 常平架铣孔过程示意图

利用百分表找正后方轴理论上完全平行于轴。随后转台绕轴旋转1-(π/2)，由轴正方向看绕顺时针旋转，所以1取负值。此时完成第一个圆孔的加工，如图3b所示。随后转台绕轴旋转2=-，完成第二个孔的加工，如图3c所示。设加工坐标系原点与零件几何中心重合，第一个孔初始点位置0(0,0,0)，旋转1后理论加工位置为1(1,1,1)，实际位置为1′（1′1′1′）。完成第一个孔加工，旋转2后理论加工位置为2（222），实际位置为2′（2′2′2′）。基于误差一致性假设，即两次旋转产生的位移误差和角误差相同，则由式（3）可得：

图4 垂直度误差模型示意图

将1-(π/2)、2=-π、（0,00）=(-2, 0, 0)及式（2）、式（3）代入式（4），并将计算结果代入公式（5），可得垂直度与转台位移误差、角误差的关系：

4 同轴度误差计算

4.1 误差模型工程转化

机床精度检测时，转台精度通常有以下衡量指标：台面径向跳动误差、台面轴向跳动误差e、平面度误差、分度精度和重复精度。在上述理论计算中，转台误差分为位移误差和角误差，由图5可以看出转台精度指标与误差的转换关系为：Δe、Δe、Δe、Δarcsin[e/22]、Δe、Δarcsin[e/21]。

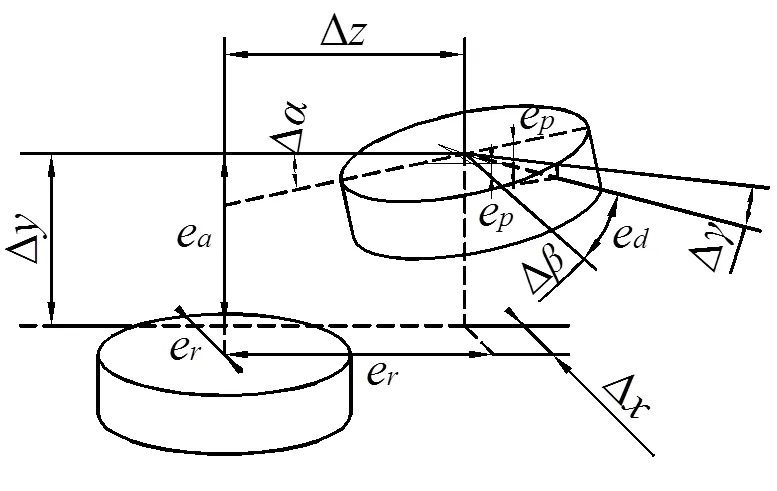
图5 转台精度与误差关系示意图

将上述换算关系代入式（6），可以得到垂直度误差的工程模型：

4.2 基于转台误差的同轴度误差计算

a 轴向跳动和径向跳动对垂直度影响

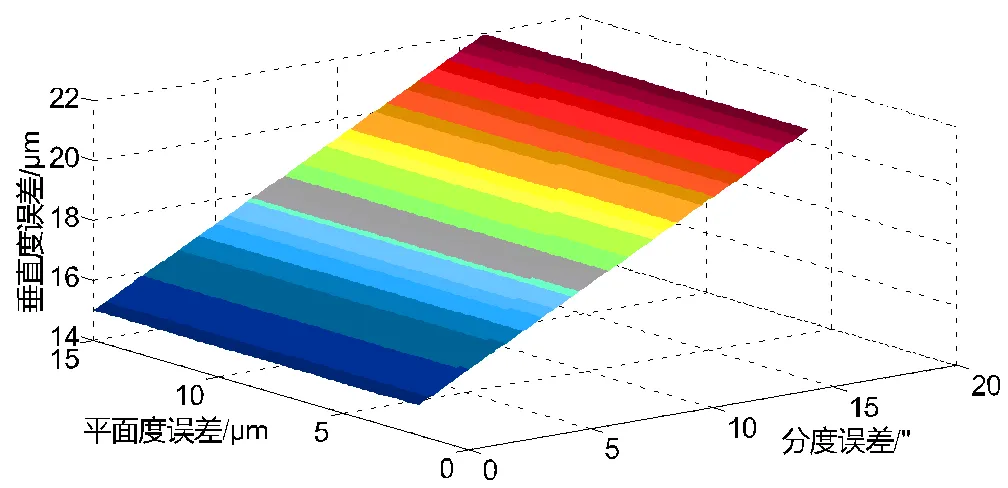
b 平面度和分度对垂直度影响

c 轴向跳动和分度对垂直度影响

d 径向跳动和分度对垂直度影响

e 平面度和轴向跳动对垂直度影响

图6 垂直度误差和转台精度指标三维图

为评估加工中心能否满足常平架加工误差，分析转台各精度指标对加工精度的影响规律，利用MATLAB工程计算软件分析垂直度误差模型。分析计算结果，由图6a、图6b、图6c可以看出，台面径向跳动误差、分度精度对孔轴线垂直度的影响要远大于台面轴向跳动误差e和平面度误差。由图6d可以看出，径向跳动误差和分度精度对垂直度影响作用相当，径向跳动误差更为明显。与实际情况吻合。由图6e可以看出，平面度误差对垂直度影响更大。

其他三项因素固定，分别分析单因素对垂直度误差的影响，如图7a、图7b、图7c、图7d所示，对影响垂直度误差的影响排序，径向跳动误差斜率＞分度精度＞平面度误差＞轴向跳动误差。

5 加工试验

表1 试验设备转台精度

在德玛吉加工中心DMU 100P、DMU 80P、DMU 80monoBLOCK上进行常平架铣圆孔加工试验，这三台设备均为转台-摆头式五轴加工中心。根据机床检测部门提供的检测数据，三台加工中心的转台精度如表1所示。

在三台机床上，用同样的工艺方法和加工参数，分别加工10件常平架，如图8所示。加工后对试件垂直度进行计量，计量结果如表2所示。

图8 常平架加工试验

表2 试验件垂直度计量结果

由加工试验结果可以看出：径向跳动误差和分度误差小的机床加工后的常平架垂直度符合公差要求，而轴向跳动误差和平面度误差越大，加工后的垂直度不一定越大。从影响程度来看，径向跳动误差和分度误差对垂直度的影响大于平面度误差和轴向跳动误差。模型计算与试验结果有较好的一致性。

6 结束语

通过常平架正交孔系垂直度误差模型的计算和试验，可以得出以下结论：

a. 在加工中心转台的5项精度指标中，径向跳动误差和转台分度误差是影响垂直度结果的最关键因素，其中径向跳动误差的影响更大。

b. 基于齐次坐标变换理论建立的垂直度误差模型与实际加工结果具有较好的一致性。

c. 三台加工中心中，DMU 100P和DMU 80P各项精度指标相当，但DMU 80P由于转台径向跳动误差小，具备转台分度误差自动补偿功能，加工后的常平架垂直度误差满足要求，一致性好，更适合用于常平架铣圆孔的加工。在DMU 80P上加工产品，一批产品加工后的垂直度计量结果均满足要求。

1 朱宁昌. 液体火箭发动机设计（上）[M]. 北京：宇航出版社，1994：277

2 栗时平. 多轴数控机床精度建模与误差补偿方法研究[D]. 长沙：国防科技大学，2002

3 任永强，杨建国，基里维斯，等. 四轴数控机床误差综合建模原理及分析[J]. 机械工程师，2003(8)：18～22

4 徐旭松，杨将新，曹衍龙，等. 基于齐次坐标变换的制造误差建模研究[J]. 浙江大学学报：工学版，2008，42(6)：1021～1026

5 高焕明，杨功流，李星，等. 基于齐次坐标变换的陀螺框架加工误差分析[J]. 天津大学学报：1017～1020

6 周晓婷. 基于机床误差建模的加工精度预测研究[D]. 济南：山东大学，2016：23～24

7 张舒洁. 数控机床运动误差分步辨识法理论与实验研究[D]. 上海：上海交通大学，2010：14

Error Analysis of Bearing Hole Machining of Gimbal Mount Used in Attitude and Orbit Control Engine

Zhang Xiaofeng Li Xuguang Liu Jun

(Xi’an Aerospace Engine Co., Ltd., Xi’an 710100)

The vertical degree of two couple bearing holes of gimbal mount used in attitude and orbit control engine is hard to guaranteed. Based on homogeneous coordinate transformation, a machining error model for the boring of the 5-axis machining center is established. The vertical degree errors are analyzed by the error model using MATLAB software. The test results show that calculation errors are similar to the test data. The error calculation contributes to ensuring accuracy of vertical degree of bearing holes in gimbal mount.

gimbal mount；bearing holes；vertical degree；homogeneous coordinate transformation；error model

V431

A

张晓峰（1991），工程师，航空宇航制造工程专业；研究方向：液体火箭发动机阀门制造。

2020-12-20