支座约束对大跨度条形仓上部结构的影响

李 影

（中交第一航务工程勘察设计院有限公司，天津 300222）

1 工程概况

唐山港京唐港区某堆场条形仓，全长855 m，设置9个仓，各仓之间设置12 m的消防通道以满足防火要求。堆场条形仓采用空间钢管桁架结构（三心圆柱面），净空高度为40.138 m，跨度为131.6 m，每榀桁架每侧三个柱脚，基础采用桩基础。

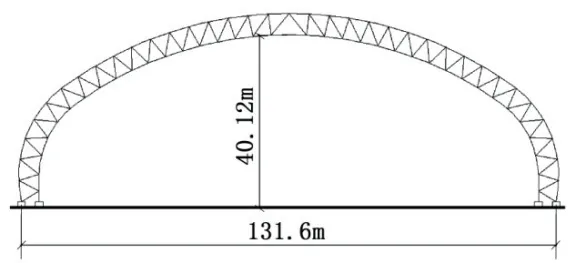
图1 条形仓剖面

2 支座约束假定

上部结构的荷载通过支座传给基础，因此，条形仓的支座节点必须具有足够的强度和刚度。支座应做到传力可靠，连接简单，并应符合计算假定。拟采用成品固定抗拔球铰支座，该支座型式是在国标球型支座的基础上升华而来的。可分为固定型，单向位移和双向位移三种型式。根据条形仓的支座，本文提出两种支座约束假定。

2.1 固定支座假定

空间钢管桁架的支座约束，都是支座在支座反力作用下，对线位移的约束。支座在支座反力的作用下，X、Y、Z三个方向都不产生线位移，即为固定支座。

2.2 弹性支座假定

如果支座在支座反力的作用下，X、Y、Z某一个方向或多个方向产生一定的位移，同时能保证空间钢管桁架的稳定，我们称此支座为弹性支座。

不同的支座约束形式和不同的弹性支座刚度，对大跨度条形仓的上部钢结构的杆件应力、桁架的位移及支座反力都会产生很大的影响，支座反力的不同又会影响基础的受力。因此不同的支座约束假定，将直接影响结构的安全及工程造价。对于类似本工程的大跨度钢管桁架结构，计算时不应只取一种支座约束假定，而应对比不同的支座约束对上部结构和下部基础的影响，综合考虑。

3 不同支座约束假定下上部结构的分析

本工程计算时对支座提出三种约束假定，首先，是固定支座假定；其次，是以规范计算得来的支座弹性刚度假定（方法一）；最后，是以实际试桩结果计算得来的支座弹性刚度假定（方法二）。支座约束假定如图2～图3及表1。

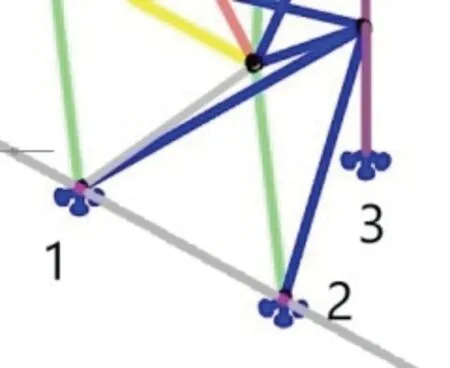
图2 条形仓单榀一侧的柱脚

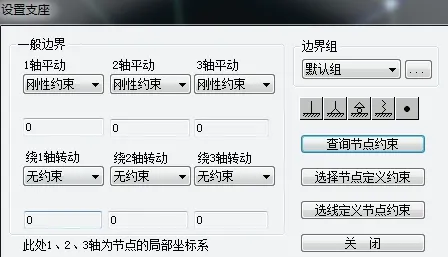
图3 固定支座约束假定

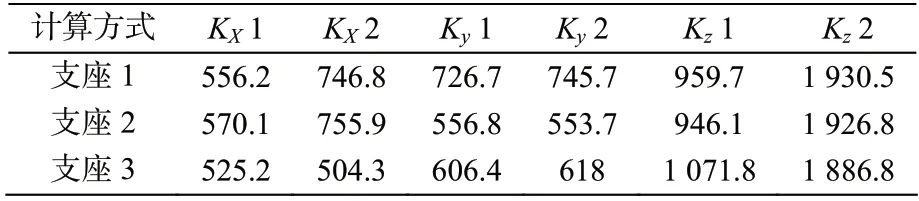
表1 两种弹性支座刚度的取值/(kN·mm-1)

不同支座约束下堆场条形仓单仓的周期如表2（仅截取前5个振型）。

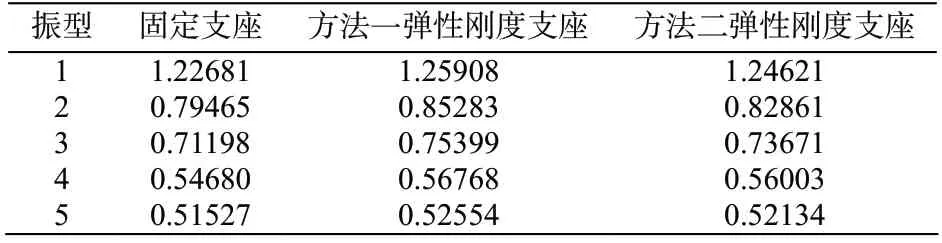
表2 上部钢结构周期计算结果/s

由表2结果可以看出，支座刚度越大，结构周期越小，该趋势符合力学计算原理，可以进行计算结果分析。

以一个分仓的同一榀桁架的计算结果为例，对比不同支座约束假定下对上部结构受力的影响。杆件分段如图4；计算结果如表3。

图4 条形仓一榀桁架杆件分段

表3 上部钢结构强度验算应力比计算结果

由表3结果可以看出，靠近支座处的上下弦杆和腹杆受支座影响较大，且支座刚度越大杆件内力越大；远离支座处的上下弦杆和腹杆，杆件内力随刚度的增加而有所减小，但总体变化不大，结果基本一致。

表4 上部钢结构位移计算结果/mm

堆场条形仓三种支座约束假定下，单拱桁架的竖向位移计算结果如表4。固定支座时结构的竖向位移最大值为188 mm，挠跨比1/700；方法一支座弹性刚度较小时，结构的最大竖向位移为192 mm，挠跨比1/685，与方案二支座弹性刚度较大时的计算结构位移近似，但仍可看出，支座刚度越大，结构的位移越小。

4 不同支座约束假定下的支座反力

选取一个分仓的同一榀桁架同一侧柱脚，对比不同支座约束假定下对支座反力的影响。支座受力示意见图2。

4.1 固定支座反力

1）外拔内压组合（恒+风+0.6温度）

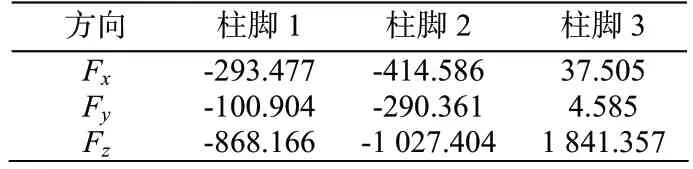
表5 各柱脚支座反力 /kN

2）外压内拔组合（恒+0.5雪+0.5积灰+水平地震+竖向地震）

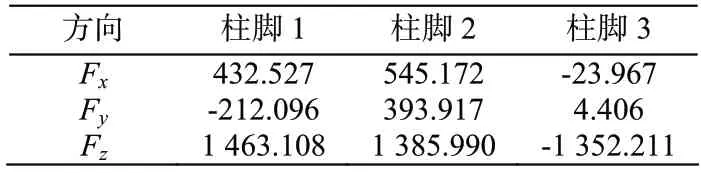
表6 各柱脚支座反力 /kN

4.2 方法一弹性刚度支座反力

1）外拔内压组合（恒+风+0.6温度）

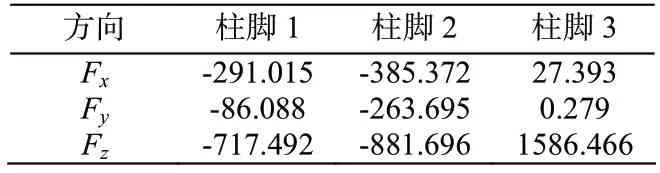
表7 各柱脚支座反力 /kN

2）外压内拔组合（恒+0.5雪+0.5积灰+水平地震+竖向地震）

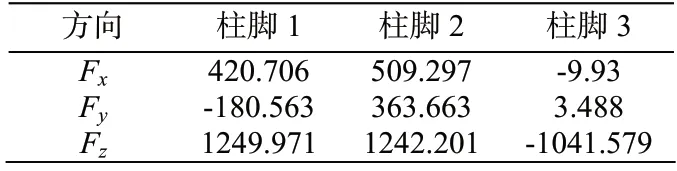
表8 各柱脚支座反力 /kN

4.3 方法二弹性刚度支座反力

1）外拔内压组合（恒+风+0.6温度）

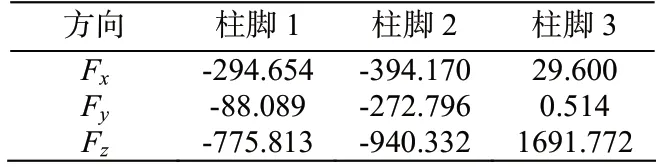
表9 各柱脚支座反力 /kN

2）外压内拔组合（恒+0.5雪+0.5积灰+水平地震+竖向地震）

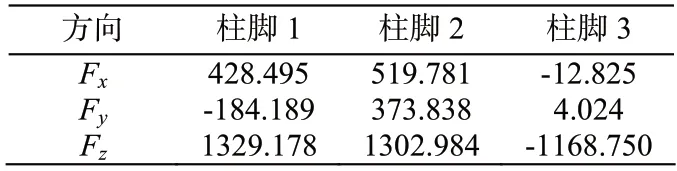
表10 各柱脚支座反力 /kN

由以上结果可以看出，支座刚度越大支座反力亦越大，水平方向的支座反力受支座刚度的影响较小，但竖向力受支座刚度的影响较大，设计时应该引起注意。大跨度条形仓的支座情况，并非是绝对的固定支座，或绝对的某一弹性刚度支座，很可能是介于二者之间的情况。因此，合理确定支座刚度尤为重要，条件允许的情况下建议包络设计。

5 结语

通过前文分析可得到以下结论：

1）靠近支座处的杆件受支座刚度影响较大，杆件内力随支座刚度的增大而增大。

2）支座刚度越大，结构的位移越小。

3）支座反力随支座刚度的增大而增大，竖向力受支座约束假定的影响较大，设计时应该引起注意。

4）合理确定支座约束假定，明确大跨度条形仓的支座应是介于固定支座和某一弹性刚度支座之间的情况，条件允许的情况下，应该多种支座约束假定综合考虑。