平均拉应力对管线管疲劳寿命的影响*

陈 燕，黄兆力，刘江成，张哲平，张传友，李 艳，张国柱

（1.天津钢管制造有限公司，天津 300301；2.中海石油（中国）有限公司海南分公司，海南 海口 570100）

疲劳断裂是油气长输管线常见的一种失效形式。管线管在服役过程中会受到各种交变应力的作用。对于陆地管线，交变应力一方面来自于管内输送压力的波动和气体介质的分层结构[1-3]，另一方面来自于管线外部的变动载荷，如埋地管线上车辆引起的振动、沼泽地管线浮力的波动、沙漠管线流沙的迁移等，另外也会由于穿越河流跨越峡谷等方面的需要形成局部管跨，在脉动风载荷的激振下，会使管跨发生振动，从而使管线受到交变应力的作用[4-7]。对于海底管线，在海浪、海流的作用下，其某些部位周围的土壤会被冲刷掉，以致于管线下面被掏空形成管跨，在海浪和海流引发的涡旋的激发下，都会使管跨发生振动，从而使得海底管线受到交变应力的影响[8-10]。深海立管是海洋工程系统重要的组成部分，在海浪、涡流、内压作用的影响下，其也是海洋管道系统中薄弱易损的构件之一，尤其是触地点和顶部连接处极易受到疲劳损伤，因此对立管的耐疲劳性能要求极高[11-12]。

管线管在以上工况服役的情况下，极易受到循环加载，管材的疲劳寿命受到如环境温度、残余应力、平均应力等多种因素的影响，平均应力为拉应力时，会降低材料的疲劳寿命，造成疲劳失效。但是，对于平均拉应力对管线疲劳寿命的影响和平均拉应力下疲劳寿命的估算还没有系统研究；因此，这里针对平均拉应力对管线疲劳寿命的影响以及平均拉应力下疲劳寿命的估算进行试验和研究，并对平均拉应力下管线管的应力-寿命曲线（S-N 曲线）进行预测。

1 疲劳行为及S-N 曲线

1.1 疲劳载荷的描述

材料的疲劳试验中，都会涉及在最大应力水平和最小应力水平之间的循环加载，而且它们都是恒定不变的，这种情况称为恒幅加载。恒幅加载疲劳谱线如图1 所示。

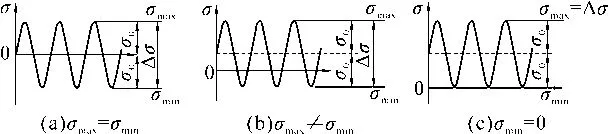
图1 恒幅加载疲劳谱线示意

应力范围是最大应力和最小应力之间的差值（Δσ=σmax-σmin）；最大应力值和最小应力值的平均值即为平均应力σm，平均应力可能是0，但多数情况下不为0；应力范围的一半为应力幅值σa，它相对于平均应力而变化，它们的数学表达式为：

此外，疲劳加载过程还将用到应力比R 以及幅值比A，其定义为：R=σmin/σmax，A=σa/σm。因此，疲劳载荷之间的关系可以进一步描述为[11]：

不同类型的循环疲劳载荷可以通过以上物理量进行描述。平均应力为0 的循环应力可以通过幅值σa来定义，如果平均应力不为0，则需要两个独立的值来定义载荷。如图1（a）所示的完全反向循环载荷，可以用σm=0 或R=-1 描述；如图1（c）所示的零-拉伸加载，可以用σmin=0 或R=0 描述。

1.2 S-N 曲线

在不同应力水平下对材料进行循环应力疲劳试验，将得到不同循环次数的试验结果。由每次试验的循环次数Nf与应力幅值σa坐标（Nf，σa）经过绘图即可得到一条应力-寿命曲线（S-N 曲线）。

失效循环次数会随着应力水平而迅速发生变化，其变化范围可能会涵盖几个数量级，因此通常将循环次数按对数坐标进行绘制。如果S-N 曲线在对数坐标中接近直线，就可以通过数据拟合方法获得该曲线的数学表达式。对于应力控制的高周疲劳行为，材料通常承受弹性应力，采用经验公式（3）得到的预测值与试验结果吻合度较高[13]。

公式（3）在对数坐标系中是一条直线，A=2bσf′。其中，σf′是无缺口试样的真实断裂强度，MPa；b是材料常数，在完全反向载荷（σm=0）条件下可以通过数据拟合得到，也可以通过材料疲劳手册查询。

2 平均拉应力对疲劳寿命的影响

2.1 应力幅值的归一化和附加平均应力方程

某钢材的恒疲劳寿命曲线如图2 所示[11]。可以看出，当试样承受的平均应力σm逐渐增大，若要保持疲劳寿命不变，必须减小应力幅值σa，否则平均应力的增加会导致疲劳寿命下降。

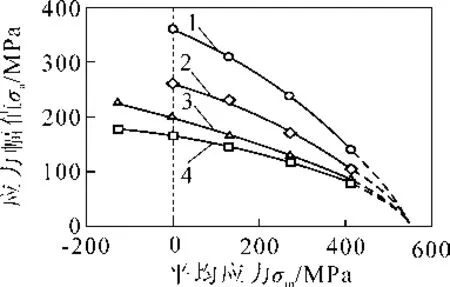
图2 某钢材的恒疲劳寿命曲线

每一种不同的平均应力σm试验条件分别对应一条S-N 曲线，每条曲线具有不同的应力幅值σa，这就为评价平均应力对材料疲劳寿命的影响带来不便，因此需要将疲劳试验中不同的应力幅值归一化处理为σa/σar。其中，σar为图2 所示σm=0 处的应力，即是等效的平均应力为0 的应力幅值。令σm=0 时的应力幅值σa=σar，即σa/σar=1；而σm≠0 时的σa/σar1，归一化应力幅值-平均应力曲线如图3 所示。此时，所有的数据点按集中趋势分布，就可以用一条曲线方程进行描述，这为分析材料的疲劳寿命提供了便利。

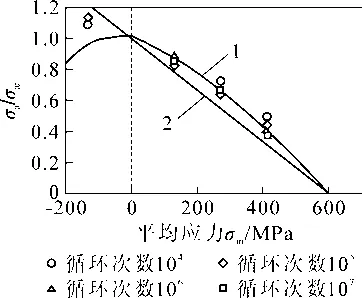
图3 归一化应力幅值-平均应力曲线

关于附加平均应力方程，目前有多种模型进行描述。

（1） Smith 于1942 年提出了直线型方程模型[14]，如图3 中直线2 所示，直线表达式为：

式中 σu—— 抗拉强度，MPa。

（5）区块写入账本。将对所有节点成功解出数学难题的广播答案进行验证，如果正确，它会将该区块纳入自己的账本中，每个节点同步进行；否则，将丢弃该区块。

（2） Goodman 在公式（4）的基础上进行了修正，利用σm=0 条件下得到的无缺口试样的真实断裂强度σf′替代σu，从而得到了修正模型[11]，表达式为：

（3） Gerber 建立了如图3 所示曲线1 的抛物线型方程[11]，表达式为：

（4） Smith、Watson 和Topper 提出了SWT 方程[15]，σmax0 时的表达式为：

SWT 方程的优点是不依赖于任何材料常数，通用性最高。

2.2 用平均应力估算疲劳寿命

由公式（4）～（7）可知，通过带入应力幅值σa和平均应力σm便可给出σar。该应力幅值与零平均应力的组合（σar，σm=0）和（σa，σm≠0）组合具有相同的疲劳寿命；因此，σar可以看做是一个等效的完全反向应力幅值，将σar带入一条零平均应力的SN 曲线，便可以对（σa，σm）组合条件下的材料寿命进行估算。

将公式（3）分别与公式（4）～（7）联立，可以得到适用于非零平均应力的、更有普遍性的S-N 寿命公式，具体如下。

（1） 由公式（4）与公式（3）联立后得到S-N 曲线公式（8）：

（2） 由公式（5）与公式（3）联立后得到S-N 曲线公式（9）：

（4） 由公式（7）与公式（3）联立后得到σmax0时的S-N 曲线公式（11）：

2.3 疲劳寿命计算

公式（8）～（11）中都可以将平均应力不为0 的疲劳载荷等效转换为平均应力为0 时的疲劳载荷，进而由平均应力和平均应力为0 时的S-N 曲线预测出平均应力不为0 时的材料疲劳寿命，从而估算出任意恒幅加载条件下的疲劳寿命。但是对于管线管疲劳寿命的计算，等效应力转化时，哪一种公式更符合该材料的疲劳特点，仍需要进一步验证。

现以X65Q 钢级管线管为例进行小试样疲劳试验。X65Q 钢级材料的屈服强度为485 MPa，抗拉强度为600 MPa。将X65Q 钢级管线管加工成棒状疲劳试样，设计试验：第1 组为平均应力为0 的试验，并得出中值S-N 曲线；第2 组试验为平均应力138 MPa 和100 MPa 时的疲劳试验；对比计算第1 组与第2 组试验的疲劳寿命，用公式（4）～（7）进行验证，确定适合X65Q 钢级材料的平均应力等效公式模型，然后再根据平均应力等效公式推导出S-N 曲线计算公式。疲劳试样加工尺寸如图4 所示。

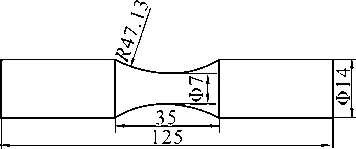
图4 疲劳试样加工尺寸示意

第1 组疲劳试验方案及其结果见表1。根据表1 中的数据，计算出每个应力水平下的疲劳寿命的平均值，再进行拟合，得到中值S-N 曲线计算公式：

表1 第1 组疲劳试验方案及其结果

观察多个第1 组X65Q 钢级管线管试样的疲劳断口形貌[16-17]，发现断口形貌相似，典型形貌如图5 所示。从图5 中可以清楚地看到贝纹线附近的试样边缘处是疲劳源，疲劳源头处没有夹杂物，分析疲劳源分布在试样表面。图5 所示的疲劳断口属于典型表面诱发疲劳裂纹萌生样品的断口形貌，可以明显看出疲劳裂纹萌生区、裂纹扩展区和瞬断区，裂纹萌生区靠近疲劳贝纹线（图5a 箭头所指位置），放大裂纹扩展区，可以明显看到疲劳裂纹向前推移的纹路（图5b）。

图5 X65Q 钢级管线管的疲劳断口典型形貌（第1 组编号2）

第2 组疲劳试验方案及其结果见表2。运用公式（4）～（7）进行计算并比较计算结果，发现Gerber建立的平均应力等效公式（6）与试验结果吻合度较高，其余公式计算的X65Q 钢级母材疲劳性能结果误差非常大；因此，Gerber 建立的平均应力等效公式（6）可以作为X65Q 钢级管线管的平均应力等效公式。针对X65Q 管线管的疲劳性能，当设计平均应力分别为138 MPa 和100 MPa 时，用Gerber 建立的平均应力等效公式（6）计算得出平均应力为0时的等效应力σar[18]，然后将σar代入公式（12），即可得出预测的疲劳寿命。表2 中的Nf的预测值就是根据拟合公式（12）计算出来的结果。对比Nf的预测值和实际试验疲劳循环次数平均值，发现预测值和试验平均值都在同一数量级，且吻合度较高。

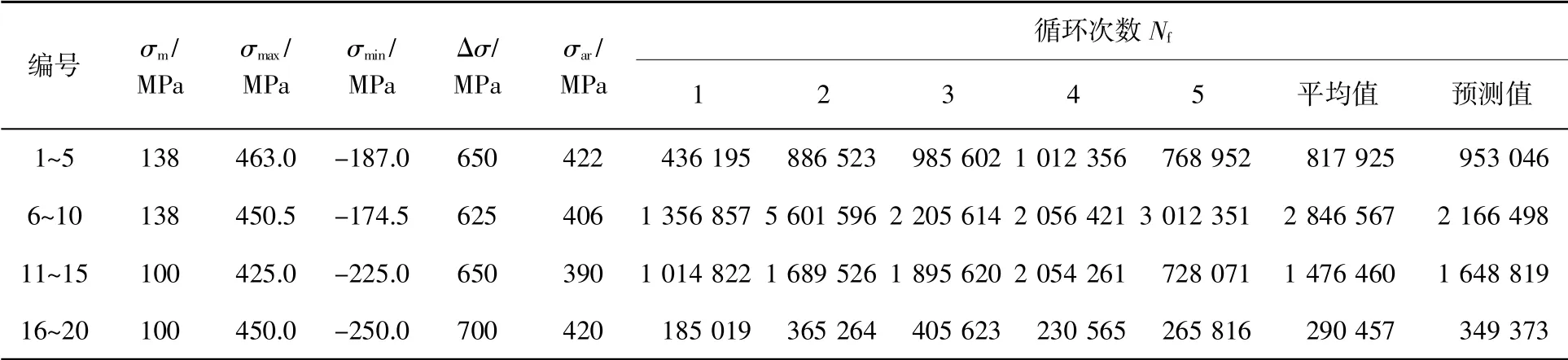
表2 第2 组疲劳试验方案及其结果

3 结 论

（1） 将σm≠0 条件下的应力幅值σa归一化处理为σar，可以使用同一个公式模型描述不同应力幅值-平均应力组合，从而得到完全反向应力幅值σar的表达式，并推导出适用于非零平均应力的、更有普遍性的S-N 公式。

（2） 对X65Q 管线管材料进行小样疲劳试验，σm=0 时的第1 组试验数据，进行中值S-N 拟合，得出S-N 曲线方程。第1 组试样的断口形貌包括典型的疲劳裂纹源、疲劳裂纹扩展区和瞬断区，从断口形貌特征判断疲劳裂纹源多发生于试样表面。

（3） 通过平均应力为138 MPa 和100 MPa 时的疲劳试验发现，相同应力范围时，增大平均应力可以明显降低疲劳寿命，且平均拉应力越大，同等应力范围下的疲劳寿命就越短；另外，用Gerber建立的平均应力等效公式（6）计算出的结果与试验结果吻合度较高。因此，可以通过Gerber 建立的平均应力等效公式和S-N 曲线方程预测X65Q 钢级管线管在非零平均应力下的疲劳寿命。