基于结构参数的机织物等效热导率数学建模
蔡彦 杨允出 钱江瑞
摘 要:通过分析织物内部组织结构,将组织循环内纱线分布按规律分6类,包括交织点纱线重叠区域、经(纬)纱交替穿越区域、经(纬)纱悬浮区域、孔隙区域。通过截面积相等的方式将不规则纱线等效转化为规则的几何体。通过分析组织循环内各区域纱线与空气分布情况,结合复合材料等效热导率串并联模型,建立各微元的等效热导率数值模型。在已建立的模型基础上进行算例分析,得到在维持其他纱线参数不变情况下,经纬纱高度增加,织物整体等效热导率增加;经纬纱间距增加,织物整体等效热导率降低;织物交织结构越复杂,悬浮区域数量占比越大,织物等效热导率降低,其中悬浮区域数量为0的平纹织物等效热导率相对最大。
关键词:热导率;机织物;数学模型;结构参数
中图分类号:TS101.1
文献标志码:A
文章编号:1009-265X(2021)02-0043-07
作者简介:蔡彦(1995-),男,浙江湖州人,硕士研究生,主要从事服装热舒适性方面的研究。
Abstract:The yarn distribution in weaving unit is classified into six categories according to the rule by analyzing the internal structure of fabric, including overlapping area of yarn at interlacing point, alternating crossing area of warp (weft) yarn, suspension area of warp (weft) yarn and pore area. The irregular yarns are transformed into regular geometries by means of equal cross-sectional area. Based on the analysis of yarn and air distribution in each area of the weaving unit and the series-parallel model of composite equivalent thermal conductivity, numerical models of equivalent thermal conductivity for each element were established. Analysis of examples based on the established models indicates that with other yarn parameters remaining unchanged, the overall equivalent thermal conductivity of fabrics increases as the yarn height increases; the overall equivalent thermal conductivity decreases as the yarn spacing increases; the equivalent thermal conductivity decreases as the complexity of the fabric interweaving structure increases and the proportion of suspended area increases. The equivalent thermal conductivity of plain weave fabrics with 0 suspended areas is relatively largest.
Key words:thermal conductivity; woven fabric; mathematical modeling; structural parameters
織物的传热性能是影响服装热舒适性的一个重要因素,在功能性服装的设计及织物服用舒适性优化中受到了广泛关注。织物,无论是机织还是针织,都由包含多孔材质纱线和孔隙的重复单元构成,其中机织物主要是由经纬纱交织而成。为了探究机织物内部传热机理,需对内部纱线及空隙的几何结构、各级材料物理属性与织物的传热性能的关系进行深入分析、建模。许多学者基于统计模型、神经网络模型、有限元方法,分形模型、物理建模等开展了关于纤维集合体或织物的内部结构对其传热性能影响、预测研究。吴海军等[1]利用相关性分析法,对不同结构参数下织物的传热性能进行了研究。李丽等[2]基于两相复合介质的等效热导率模型,运用顺变平面热源法对环氧树脂-纤维集合体进行测试,得出其等效热导率,并验证了其各向异性。肖红[3]通过构建瞬态以及稳态条件下织物传热方程,并通过制备样品测试其传热性能,验证了所建立方程的适用性。也有通过统计以及神经网络模型来分析各变量的对传热性能、热阻的影响。Bhattacharjee等[4]将各类织物参数进行组合,通过响应面统计分析法,探究各参数集体效应对热阻的影响,由于大部分织物结构参数为相互耦合关联,因此很难获得单一参数与热阻传热性能的明确关系。Bhattacharjee等[5]通过建立人工神经网络模型的方式来对qamx值和热阻进行模拟预测,虽然得到了预期的结果,但前期需要大量的数据对模型进行训练,才能得到更为准确的结果。也有学者通过对传热现象的数学分析,进行简化处理总结成物理模型,采用物理模型来对传热原理进行表征。Ismail等[6]给出了可预测平纹织物热导率的理论模型,且该模型也可用于表征纤维在织物、纱线、纤维状态下的等效热导率。Zheng等[7]通过电镜图像实测机织物的组织结构参数和纱线交织规律,利用Texgen建立了玻璃纤维平纹织物几何模型,利用有限元软件开展了织物热传递数值模拟研究。Zhu等[8]通过建立孔隙结构与多孔介质结构参数函数的方式,探究了含不饱和水分的纤维状多孔介质的有效导热模型,预计此模型可有助于评价纺织品的热舒适性。
以上关于织物传热性能的研究大都着重于传热方式以及各参数耦合条件下织物传热性能的变化情况。结合已有研究,拟从织物内部纱线几何参数与等效热导率的影响出发对织物传热进行探究。以机织物为研究对象,通过对织物组织结构及纱线几何形态的分析,对织物组织内部的纱线排列按规律进行分类;对每一类微元进行传热分析,结合复合材料等效热导率串并联模型,建立便于计算的等效热导率数值模型。并采用建立的数值模型,再从织物内纱线高度、间距及交织规律三个影响条件下对热导率变化情况进行算例分析。
1 织物等效导热系数建模
1.1 机织物组织循环的结构特征及区域划分
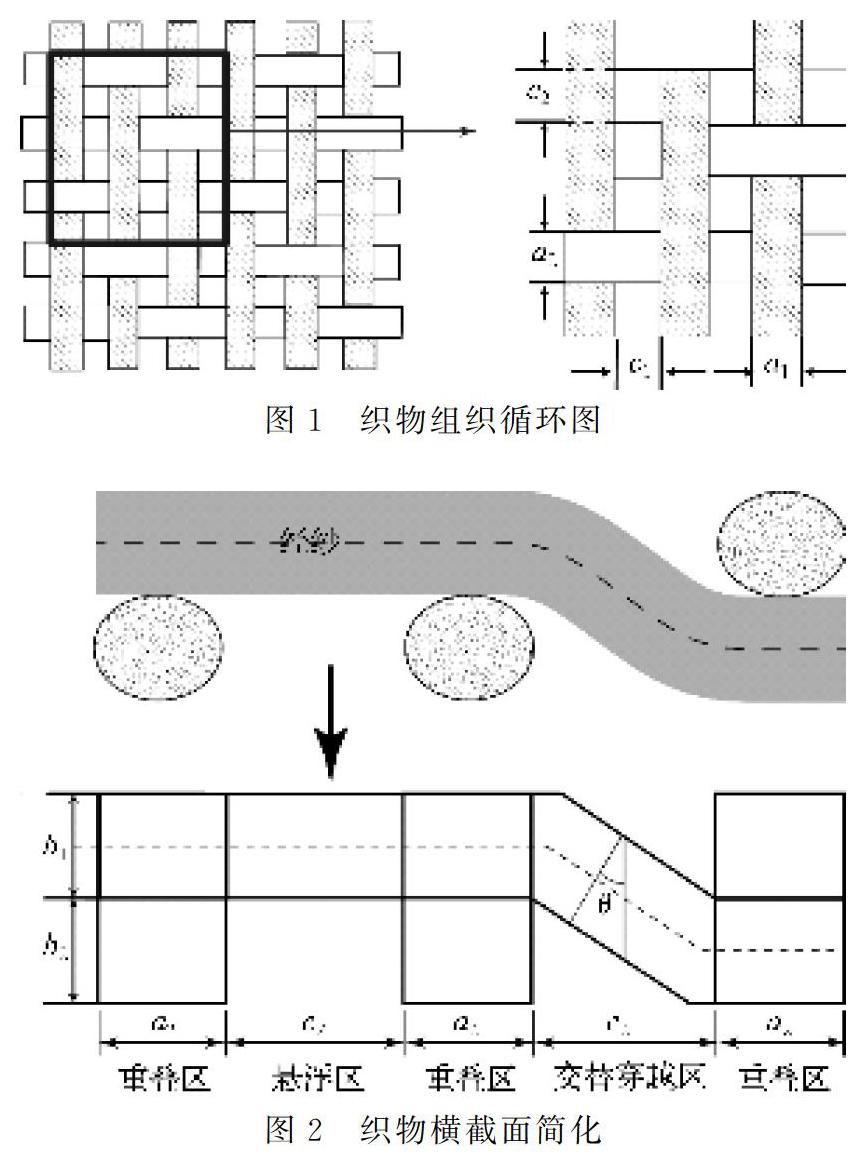
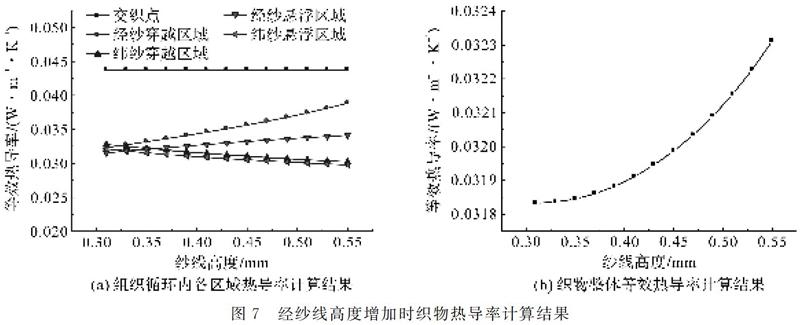
对于机织物结构形态的描述通常有以下几类经典几何模型:圆(椭圆)形、跑道模型、透镜形[9]。本文以基本组织机织物为研究对象,对组织循环单元的纱线交织结构规律进行分析和区域细分。以2上1下左斜纹为例,将该组织循环划分为交织点纱线重叠区域,纱线交替穿越区域、纱线悬浮区域和孔隙区域四类(见图1、图2)。由图1可知,该斜纹组织循环共被划分为36个基本微元区域,其中包括9个交织点纱线重叠区域(经组织点6个、纬组织点3个),12个纱线交替穿越区域(经纱交替穿越区6个、纬纱交替穿越区6个),6个纱线悬浮区域(经纱悬浮区域3个、纬纱悬浮区域3个),9个孔隙区域。为了后续构建数学模型,进一步设定该组织的相关结构参数,包括经、纬纱的宽度a1、a2,经、纬纱的高度b1、b2,相邻两经纱的间距c1,相邻两纬纱的间距c2。
椭圆织物几何模型中,经纬纱线的截面均设为椭圆形,经纬纱线的中心轴线在交替区域采用了正弦函数曲线。为了简化计算,纱线中心轴线的曲线形状转换为折线形状(见图2),将经纬纱线的椭圆截面形状采用宽度不变、面积相等的原则转换为矩形形状(见图3)。
等效转化后的经、纬纱线高度b1′,b2′取值分别见式(1)、式(2)。
1.2 基于并联模型的机织物组织循环各区域热导率计算
织物内部热量传递的方式有热传导、热对流与热辐射,大多数条件下,热对流与热辐射传递的热量相较于热传导可忽略,因此本文中对于织物内部传热的分析只考虑热传导。织物组织循环内各微元的等效热导率采用复合材料的串并联模型进行计算。当热量传导的方向与两种材料交接面平行时,为两相并联模型,总热量等于分别流过两种材料热量之和,此时等效热导率计算见式(3)。当传热方向与两种材料交接面垂直时,热量依次通过两种材料,为两相串联模型,此时等效热导率计算见式(4)。
1.2.1 交织点纱线重叠区域的热导率计算
交织点重叠区域是经纬纱交织的区域,此区域中包含两根纱线,经纬纱见图4。由图4可知,纱线交织点处可视作空气-经纱以及空气-纬纱串联的集合体,因此采用等效热导率串联模型分别计算空气-经纱的等效热导率λ1′,见式(5);空气-纬纱的等效热导率λ2′,见式(6)。
图5为纱线悬浮区域纱线分布。由图5可知,在交织点处,经纬纱呈串联,结合式(4)的串联模型,可得交织点处的等效热导率计算方法,见式(7)。将λ1′,λ2′代入式(7)可得交织点处等效热导率取值,如式(8)所示。
1.2.2 纱线悬浮区域热导率计算
经纬纱悬浮区域中只含单根的纱线,其他区域均为空气,并且悬浮区域的两侧经纬纱上下排列情况相同,见图5,以经纱为例,但又因经纬纱几何参数以及交织规律的不同而有所不同。由图5可知,此区域可视为纱线与空气的串联,根据串联模型可得经纱悬浮区域等效热导率λya的计算方法见式(9);同理,可推得纬纱悬浮区域等效热导率取值λxa,见式(10)。
式中:λxa、λya分别为经纱悬浮区域、纬纱悬浮区域的等效热导率,W/(m·K);λ1,λ2,λa分别为经纱、纬纱、空气的热导率,W/(m·K);b1、b2为纱线的高度,mm。
1.2.3 纱线交替区域热导率计算
纱线交替穿越区域中同悬浮区域类似,也只含一根纱线,但该纱线斜向穿越此区域,使得此区域两侧经纬纱上下排列顺序相反,见图6,此处以经纱为例。由图6可知,此区域内可视作是空气与纱线的串联,通过对等效转化后纱线几何形态的分析,运用式(4)计算,得到经纱交替穿越区域等效热导率λy的计算方法见式(11);同理,推得纬纱交替穿越区域等效热导率λx的计算方法见式(12)。
1.3 织物单元总等效热导率计算
以上完成了对机织物组织循环内各基本微元等效热导率计算公式的推导。而织物组织循环是由上述6类微元进行排列组合构成的。即可将每一组织循环视为多个基本微元的并联。因此计算织物整体等效热导率只需分别计算得到各基本微元体积占比,以及微元数量。由图1可知,体积占比用织物俯视图中各基本微元的面积占比表示。以图1中2上1下左斜纹织物为例,分别计算组织循环经纬向的长度l1,l2以及组织循环面积s,计算方法见式(13)-式(15)。
式中:l1,l2分别为组织循环经纬向的长度,mm;m1,m2,m3,m4分别为单根经纬纱上各模块的个数,s为组织循环的面积,mm2。
因此各模块微元的体积占比分别为:
组织循环内各微元数量与机织物的组织结构有关,结合式(4)复合材料等效热导率的并联模型,织物组织循环即织物的等效热导率计算方法见式(16)。
式中:n为组织循环内各个模块的数量,可通过确定机织物的组织循环的交织规律来确定。以图1中2上1下左斜纹织物为例,此时nxy取值为9、na的取值为9、nx与ny的取值为6、nxa和nya的取值为3。
2 结果与讨论
由上述所建立等效热导率数值計算模型可知,影响织物等效热导率的主要是两大因素:为织物内纱线交织的方式与纱线的几何参数;织物内部纱线以及空隙区域的空气(或填充物)的热导率。针对上述两类影响条件,选取图1中2上1下左斜纹织物作为算例进行分析,织物几何参数见表1。从织物内部纱线间距,纱线高度以及纱线交织规律3种影响因素条件下织物等效热导率的变化进行分析。
2.1 纱线高度对等效热导率的影响
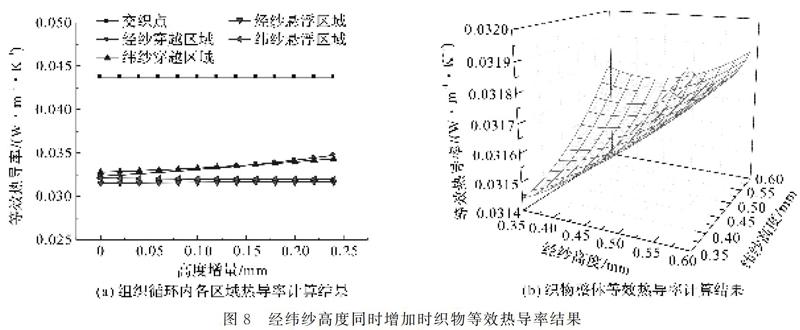
首先改变经纱高度,使经纱在原始参数基础上以0.02 mm为一个梯度逐步增加,采用已建立的数值模型计算组织循环内各区域等效热导率以及整体等效热导率,结果见图7。
由图7可知当经纱高度增加时,只包含单根经纱的悬浮区域热导率会随纱线高度的增加而逐步增大,经纱交替穿越区域热导率也同样随之增加,且增加幅度更为明显,纬纱交替穿越区域与纬纱悬浮区域热导率呈现下降趋势,交织点等效热导率未发生明显变化,织物整体等效热导率呈上升趋势。这是因为纱线高度增加使得织物内交替穿越区域与悬浮区域内纱线所占体积占比增加,从而使得等效热导率增加,反映到织物整体即为织物整体等效热导率增加。
同时增加经纬纱高度,使经纬纱高度以同样的梯度增加,代入已建立的数值模型计算,组织循环内各区域模块的等效热导率以及整体等效热导率计算结果见图8。
由图8可知,当经纬纱高度同时增加时,交织点纱线重叠区域、经纬纱悬浮区域等效热导率几乎维持恒定,交替穿越区域等效热导率则呈现增长趋势,织物整体等效热导率呈现增长趋势。这是因为经纬纱悬浮区域中,经纬纱高度同时增加时,其间纱线与空气的体积占比变化幅度很小,几乎保持不变,而经纬纱交替穿越区域中纱线体积占比会因为织物内部纱线高度增加而增加,导致等效热导率计算结果增加。纱线高度的变化不会改变纱线内各区域体积占比,因此可得纱线整体等效热导率呈现增大的趋势。
2.2 纱线间距对等效热导率的影响
改变经向纱线间距,使得纱线间距以0.04为一梯度逐级增加,采用已建立的数值模型计算组织循环内各区域模块的等效热导率以及整体等效热导率,计算结果见图9。
由图9可知,当纱线经向间距增加时交织点区域、经纬纱悬浮区域等效热导率均趋于平稳无较大变化,经纱交替穿越区域等效热导率呈下降的趋势,织物整体等效热导率也呈现下降趋势。这是因为纱线间距的增加,使得紗线分布更为疏松,交替穿越区域内纱线体积占比降低,经纱交替穿越区域等效热导率降低;且在组织循环内纯空气区域、经纬纱交替穿越区域、悬浮区域的体积占比增加,交织点区域的体积占比降低,因此织物整体热导率呈现下降趋势。
同时改变经纬纱线间距,使两根纱线间距以同样的梯度增加,代入已建立的数值模型计算,组织循环内各区域模块的等效热导率以及整体等效热导率计算结果见图10。
由图10可知,当经纬纱间距同时增加时,交织点处以及经纬纱悬浮区域的等效热导率几乎维持恒定,交替穿越区域等效热导率则呈现降低趋势。由于经纬纱间距增加,交替穿越区域内纱线体积占比降低,交替穿越区域等效热导率降低。并且经纬纱间距的增加会使得纯空气区域、经纬纱交替穿越区域、悬浮区域的体积占比增加。上述两因素共同导致了织物整体等效热导率降低。
2.3 织物交织规律对等效热导率的影响
由图1可知,织物交织规律的变化会影响组织循环的大小以及组织循环内各微元的数量,各微元数量的变化会影响织物内纱线与空气体积占比。在保持纱线参数不变的情况下,以平纹织物、2上1下左斜纹织物、2上2下方平织物为例,通过对组织结构的分析,分别计算其等效热导率,结果见表2。
由表2可知,织物类型变化时,组织循环内各区域微元总数量会变多,交织点和空气区域的数量占比均保持恒定,为总数的1/4。交替穿越区域与悬浮区域会随着组织结构的变化而发生变化,如平纹织物的经纬向交替穿越区域数量均为4,占微元总数的1/4,且不存在悬浮区域;2上1下左斜纹织物经纬向交替穿越区域的数量均为6,占微元总数的1/6,经纬向悬浮区域数量为3,占微元总数的1/12;2上2下方平织物经纬向交替穿越区域的数量均为8,占微元总数的1/8,经纬向悬浮区域数量为8,占微元总数的1/8。
织物内部组织类型的变化主要表现为交替穿越区域与悬浮区域数量的变化,由表2可知当悬浮区域数量占比增大时纱线的等效热导率会降低,平纹织物不存在悬浮区域,因此此时纱线交织最为紧密,此时织物等效热导率为三者中最大;2上2下方平织物悬浮区域数量占比最大为1/8,此时织物等效热导率为三者中最小。悬浮区域等效热导率为小于交替穿越区域的热导率,因此悬浮区域数量占比的增大会导致织物等效热导率降低。
2.4 织物热导率实验测试
基于文中对于热导率的探究,对用于算例分析的面料进行热导率测试,并与计算结果进行对比,验证模型可靠性。使用平板式保温仪测试织物的传热系数,通过计算得到织物热导率。在织物上无开边、破洞处裁取5个30 cm×30 cm的试样,分别进行测试,并取平均值,得到平均传热系数为55.43 W/(m2·K),结合织物厚度0.64 mm可计算得到织物热导率为0.035 475 W/(m·K)。采用文中建立的数值模型计算得到的等效热导率为0.031 442 W/(m·K),两者间误差值大约为11.37%,在可接受范围内,其中误差来源主要是在对于纱线进行等效转化的过程中,纱线体积发生了变化,不能做到完全等效,但热导率计算值与实验值在量级以及数值上均较为接近,因此所建立的等效热导率模型可用于对织物等效热导率进行模拟分析。
3 结 论
通过对机织物组织循环进行分析,根据纱线排列方式将组织循环内各区域分成6类微元,分别为交织点纱线重叠区域、经(纬)纱交替穿越区域、经(纬)纱悬浮区域、孔隙区域。通过截面积相等的方法,将不规则的纱线转化为规则的矩形、折线形进行计算。以复合材料等效热导率模型为基础,对各微元进行分析,并建立等效热导率计算模型;在此基础上将各微元的等效热导率模型进行整合得到织物等效热导率模型。由模型可知,在只考虑织物内部纱线层面的影响因素时,影响织物等效热导率的主要因素为织物内部纱线与空气体积占比与纱线以及空气(填充物)的热导率。其中纱线的几何参数以及交织规律的变化会影响织物组织循环内各类微元数量以及体积占比,从而影响纱线与空气的体积占比。保持织物内部其余变量均保持不变,只考虑单一变量情况时,经纬纱高度增大,会使得织物等效热导率增加;经纬纱间距增大,会使得织物等效热导率降低;织物组织循环中悬浮区域数量占比增加(及交织规律变化)会使得织物等效热导率降低,当悬浮区域数量为0是此时织物为平纹组织,等效热导率为同等纱线参数条件下最大。

