基于改进K均值聚类算法的摩斯报抄报研究*

梁 充

（杭州电子科技大学，浙江 杭州 310018）

0 引言

摩斯（Morse）报是短波无线通信的主要应用之一，也是通信的重要手段之一。摩斯报的优点是编码方式简单、抗噪性强且易于实现。尽管随着通信技术的飞速发展摩斯报的应用受到了极大影响，但不管是某些民用通信领域还是军事通信领域仍然应用着摩斯报，如无线电广播、航空公告、海上通信以及战备演习等[1]。

摩斯报发送的是摩斯码。摩斯码由2种码和3种间隔组成。2种码分别为点（dot）与划（dash）；3种间隔分别为码间隔、字符间隔以及字间隔.点的时长为基本单位，划的时长为点的3倍，码间隔与点相同时长，码间隔、字符间隔以及字间隔的时长比例为1:3:7[2-5]。点与划的不同排列组合代表了不同的字符，而每个字符中点与划的间隔为码间隔，字符之间的间隔为字符间隔，字符组合为单词，单词之间的间隔为字间隔。

然而，在实际发报时存在大量人工发报和人工值守抄报的情况，使得人工摩斯码的参数并不能完全精确为1:3:1:3:7，只能相对接近码文标准，且稳定性较差。对于不同的发报人，点的时长也不尽相同，导致译码难度大幅上升。在人工抄报方面，由于人的反应能力有限，随着时间的持续以及报文数量、信息量的增加，报务员需要对接收到的摩斯码进行高效快速的抄报，往往导致正确率大大下降。此外，长时间、强噪声环境下的监听抄报对报务员也会产生身体健康影响[6-8]。近年来，一些文献使用了机器学习中的聚类方法进行对摩斯码的自动抄报，如K均值聚类算法（K-means）、模糊C均值聚类算法（Fuzzy C-Means，FCM）等。尽管在信噪比较低的情况下它也得到了不错的效果，但耗时较长。受此启发，本文基于K均值聚类算法的原理，根据摩斯码的特性改进算法，并将其应用于摩斯报的自动抄报。实验表明，在相同环境下，该改进算法的抄报效率同比于原算法的抄报效率有了较大提升，且能保持原算法的高抄报准确率。

1 信号预处理

1.1 时频分析

摩斯信号在时域与频域中均有重要的特性，因此目前常用时频联合域分析（Joint Time-Frequency Analysis），即时频分析作为处理摩斯信号的方法。时频分析方法能够提供摩斯信号在不同时间与频率下的能量密度信息，有利于下文针对摩斯信号进行的降噪处理。短时傅里叶变换（Short Time Fourier Transform，STFT）是时频分析中较为常用的一种方法[9]。本文利用式（1）和式（2）对摩斯信号进行短时傅里叶变换得到时频矩阵Pn(ω)，式中x(m)为采集到的连续摩斯信号，n为时间，ω为频率。将其进行灰度映射可得到时频图，如图1所示。

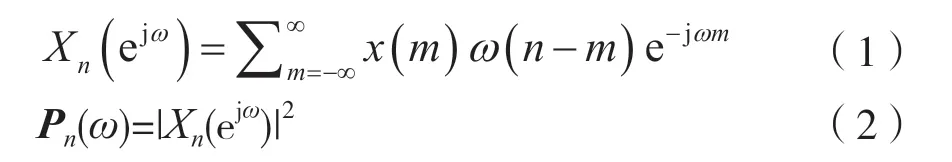
图1 摩斯信号时频图

由图1可见，摩斯信号的时频特征为矩形亮条。矩形亮条在时间轴上的长度就是码的长度，其中亮条按照1:3的长度比例对应摩斯码中的点与划，每段亮条之间的间隔也根据1:3:7的长度比例分别对应摩斯码中的码间隔、字符间隔以及字间隔。图1中的摩斯码为“......-...-..--- -----.-.....”，对应的报文为“HELLO MORSE”。

1.2 灰度变换

在实际情况下，摩斯信号中会夹杂着大量噪声。仿真下的高斯白噪声反映在时频灰度图中表现为大小、形状、灰度均各异的亮斑，不利于提取有用信号。对此，本文采用灰度指数变换的方法将摩斯信号时频灰度图中的高灰度级（即有用信号部分）进行扩展，同时将低灰度级（即噪声信号部分）进行压缩，从而更好地分离有用信号与噪声信号，计算公式为：

式中，f(x,y)为原图像的灰度分布，a、b、c用于控制灰度值扩展与压缩的范围与程度。

1.3 阈值分割

在处理摩斯信号时频图到分析时频图并译码的过程中，图像分割是关键步骤。常用的图像分割方法有许多种，如种子填充、边缘分割、区域分割以及阈值分割等。对于摩斯信号时频图，信号与噪声混杂在一起。本文采用最大类间方差法得到自适应分割阈值，并对图像进行阈值分割，将信号部分与背景噪声分开得到信号的二值图。

2 摩斯码译码

2.1 参数提取

已知点、划、码间隔、字符间隔、字间隔的长度比例为1:3:1:3:7，通过提取分析矩形亮条以及间隔在时间轴上的相对长度，即可判断某个矩形亮条是点还是划、间隔是什么类型的间隔，再以字符间隔或字间隔将矩形亮条正确分组，每组即为一个字符，然后对照摩斯电码表进行译码。参数提取与归一化的目的就是将摩斯码的二值图信息转化为码和间隔的相对长度信息。将二值图用由0、1组成的矩阵表示，计算得到每一段0与1的长度，再将所得的所有长度分别除以其中的最大值，通过归一化得到它们的相对长度，得到0、1的相对长度分布图，如图2所示。由图2可以发现，五类码有其各自的聚集特性。为了区分它们，本文采用聚类算法。聚类算法是机器学习中的一种非监督学习算法，特点就是没有任何的先验假设，在处理数值型数据集时具有很好的表现，且非常适用于处理像摩斯码长度参数这样能够被明显区分为不同区域且辨识度较高的数据集。

图2 五类码的分布情况

2.2 改进聚类算法

K均值聚类（K-means Clustering Algorithm）是一种较为常见的分类式聚类算法，用于将原始数据集中的样本分类到多个聚类中心[10]。K均值算法由以下过程迭代式地进行计算：

（1）设定K个聚类中心点；

（2）将这K个点随机放置，完成初始化；

（3）分别计算原始数据集中每个样本点到每个聚类中心点的欧氏距离，将样本点归类至距离最近的聚类中心点所在的类，且在一轮运算后，原始数据集被分为K类；

（4）根据K个类中所包含的样本点，重新计算每一类中样本点的均值中心，作为新的聚类中心点；

（5）再次更新样本点的归类结果，根据新的聚类中心点重新计算样本点距离并划分出K个类；

（6）重复步骤4和步骤5，直至所有样本点所属的聚类中心不再发生变化或满足一定的迭代次数。

以上就是K均值算法的全过程，通过迭代来更新聚类中心点与其样本区域，直至无法更新[11]。初始化时，聚类中心的位置非常重要。在K均值算法中，因为不同的初始位置可能会导致不同的结果，所以一般要求聚类中心尽量分散开。但是，对于分析聚类摩斯码的码长这一特定情况，本文在初始化时对聚类中心的位置做了理论运算。根据摩斯码的点、划、码间隔、字符间隔、字间隔码长比例为1:3:1:3:7，可得在理想情况下五类码的码长归一化分布应为：点（1，0.143）、划（1，0.429）、码间隔（0，0.143）、字符间隔（0，0.429）、字间隔（0，1）。以此对应初始化时5个聚类中心的位置，可以大大降低聚类算法的迭代次数，并且避免随机到不同初始化聚类中心而导致聚类结果不同的情况。由此，本文提出了一种基于改进K均值聚类算法的摩斯码译码方法。

（1）将摩斯码二值图所转化的矩阵中0、1的时间长度进行归一化；

（2）设K为5，将5个聚类中心初始化为（1，0.143）、（1，0.429）、（0，0.143）、（0，0.429）、（0，1）；

（3）用K均值聚类算法进行迭代；

（4）将5个聚类下的5类样本点分别对应点、划、码间隔、字符间隔以及字间隔，得到摩斯码并查表译码。

3 仿真实验与结果分析

仿真环境为高斯白噪声AWGN信道，实验步骤如下。

（1）将载有“HELLO MORSE”信息的摩斯信号音频文件导入仿真软件MATLAB R2017b，添加0 dB的高斯白噪声，以短时傅里叶变换STFT作出时频图。

（2）将摩斯信号时频图进行灰度映射，使其变为灰度图，如图3所示。后对其进行灰度指数变换处理，得到图4。通过对比图3、图4，结合图5，可以明显看出，经过灰度指数变换后，灰度图的对比度增大明显，灰度分布更加分散，降低了阈值分割的难度。下面通过最大类间方差法获得自适应分割阈值，再以此阈值对图像作分割处理得到图6。

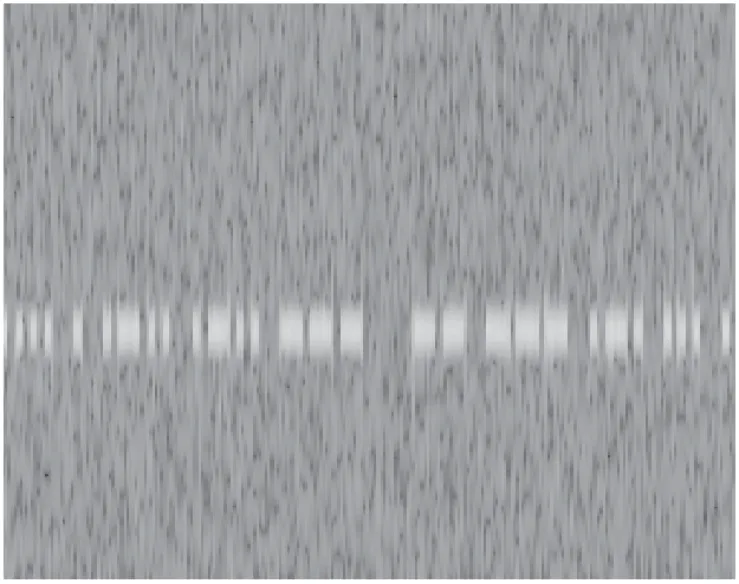
图3 灰度映射后的摩斯信号时频图

图4 灰度指数变换后的时频图

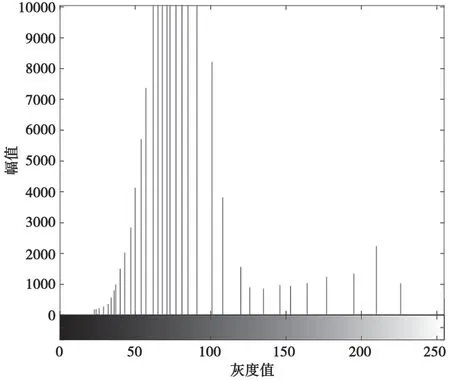
图5 参数为0.06时的图像灰度分布

图6 阈值分割后的图像

将分割后的二值图作参数提取并归一化作出分布图，如图7所示。阈值分割有时并不能完美地将噪声与信号分离，在分割后得到的图像中仍然会存在一些毛刺。对于二值图的参数矩阵中所有包含信号的行，只需要提取其中的一行参数，即可进行点、划以及间隔的识别。因此，本文在参数提取时，只要求挑选与其他行相比相似度最高的行，从而避免提取到带有毛刺的部分。

图7 归一化后的0、1参数分布

分别以K均值聚类算法和本文中改进的K均值聚类算法处理分布图，过程中计时，处理后对照摩斯码表翻译报文，结果如图8和图9所示。

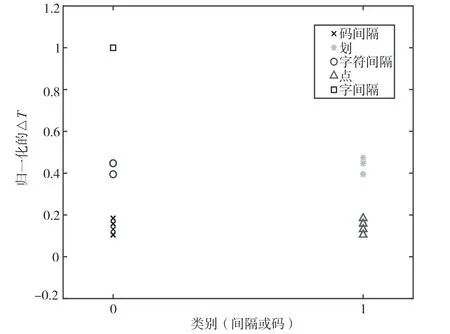
图8 聚类结果

图9 输出识别结果与对应码文

改变信噪比，对比在不同信噪比下算法的性能与准确率。对于一段码文长度为100、内容信息随机的摩斯码，在其他相同环境下添加信噪比范围为-10～5 dB的高斯白噪声，用本文算法进行抄报识别。为了更加准确地统计算法的准确率，以点划与间隔的结果进行对比，免去将摩斯码译码过程中可能造成的误差，实验结果如图10所示。从图10可以看出，当信噪比大于-5 dB时，算法的准确率较高，能达到95%以上，而在信噪比为-9 dB时仍能达到85%的准确率。

生成多个不同长度的随机摩斯信号，在0 dB的高斯白噪声环境中重复步骤1～步骤4，比较两种算法所需要的时间，实验结果如图11所示。由于两种算法耗时都非常短，为了便于比较，将时间参数乘以10 000。从图11可以看出，随着长度的增加，两种算法的耗时都有所增加，但是改进算法不仅耗时更短，而且增长率更高。

图10 不同信噪比下的算法准确率情况

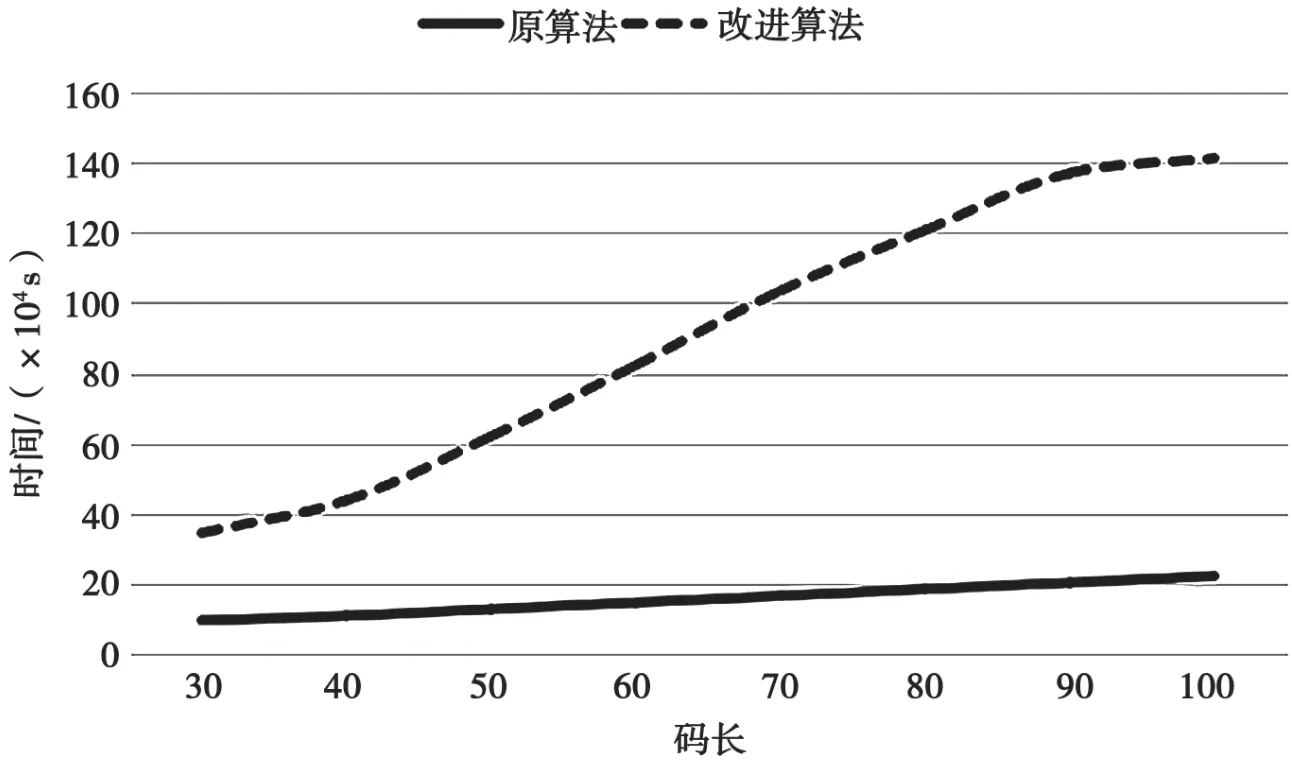
图11 两种算法的耗时对比

4 结语

根据现有的摩斯码抄报方法，结合摩斯码本身的一些特性，本文提出了一种基于改进K均值聚类算法的摩斯码抄报方法，更加适用于摩斯码的抄报。该方法先采用时频分析将摩斯信号的分析转化为时频图像的分析，后经过灰度映射、灰度指数变换以及阈值分割等方法进行去噪处理。对于去噪效果不甚完美的部分，在参数提取中将其舍去，从而保证得到的参数最为准确。参数提取后进行归一化，作出分布图，并对其采用改进的K均值聚类方法识别标记出摩斯码中的3种码和3种间隔，后对照摩斯码表最终得到抄报结果。本文方法简单，且采用非监督学习算法，无需先验信息。在仿真实验中，通过统计不同信噪比下的算法准确率和对两种算法的耗时统计，验证了本文方法较高的准确性和高效性。如何在摩斯码译码过程中再一步提高效率，是下一步的研究内容。