织物表面疵点检测方法的设计与实现

俞新星　任勇　支佳雯

摘要：针对传统织物生产企业中，人工检测织物存在瑕疵检出效率低、误检率高的问题，提出了一种织物表面疵点检测方法。该方法首先采用高斯滤波、线性归一化以及限制对比度自适应直方图均衡化对织物表面图像进行预处理，从而有效增强图像中的疵点表现细节，然后通过改进的Gabor优化选择，再对选择后的图像进行初分解，从中挑选出最优滤波图像进行二值化处理，最后运用统计学方法进行疵点判断并获得最终结果。该方法实现简便、硬件要求低、适应性广，可用于判断织物表面是否含有疵点，并定位疵点。实验证明，织物表面疵点检测准确率高达95.38%。

关键词：织物疵点检测;Gabor优化选择;直方图均衡化;线性归一化

中图分类号：TS103;TP391

文献标志码：A

文章编号：1009-265X（2021）01-0062-06

Abstract：Toaddresstheproblemsoflowdefectdetectionefficiencyandhighfalsedetectionrateofmanualfabricdetectionintraditionalfabricmanufacturingenterprises，afabricsurfacedefectdetectionmethodisproposed.Forpurposeofthismethod，theGaussianfilter，linearnormalizationandlimitedcontrastadaptivehistogramequalizationareadoptedforpreprocessingfabricsurfaceimages，todisplaydetectdetailsoftheimagesclearly.Secondly，theselectedimagesarepreliminarilydecomposedviaimprovedoptimalGaborfilter，withaviewtopickingouttheoneswiththeoptimalfilteringforbinarizationprocessing.Lastly，defectjudgmentisconductedbymeansofstatisticalapproach，andthefinalresultisobtained.Themethodiseasytooperate，haslowrequirementsintermsofhardware，andisofwideadaptability.Itcanbeusedtojudgethepresenceofdefectsonfabricsurface，andlocatethem.Themethodisprovedtohaveanaccuracyrateoffabricsurfacedefectdetectionashighas95.38%throughexperiments.

Keywords：fabricdefectdetection;optimalGaborfilter;histogramequalization;linearnormalization

作者簡介：俞新星（1998-），男，江苏如皋人，2017级软件工程专业本科生。

织物的疵点检测是纺织工业中一项十分重要的环节。传统的织物疵点检测通常由人工完成，缺乏统一的疵点评判标准，且存在检测速率与精度低、漏检与误检率高等问题[1]。因此寻求快速精确检出织物疵点的方法成为现代化纺织业亟需解决的问题。

目前普遍采用机器视觉的方法进行织物疵点检测。其中，织物瑕疵特征提取算法是织物疵点检测的核心，针对织物疵点检测算法主要基于模型的方法，有基于统计学的方法，基于谱分析的方法等。基于模型的方法需要构建模型并对各种织物瑕疵进行提取与训练，Ngan等[2]运用基元的对称性在不同基元之间移动计算能量方差，运用统计学方法得出方差的边界条件，进而识别疵点;基于统计学方法主要是利用像素的统计特征进行瑕疵检测，Aura等[3]运用分形维理论检测织物表面的疵点，其准确率高达96%，但是精准度不高，Bodnarova等[4]采用结构文理分析方法，用来自多模板的相关系数产生疵点的相关映射图，该方法鲁棒性不强，容易受到外界因素的干扰，且在特殊模板与窗口尺寸的选择上拥有困难;基于谱分析的方法主要基于傅里叶变换、小波变换或者Gabor变换等将织物图像转换到频域来实现瑕疵检测，其中由于Gabor变换具有时频分析的特点[5]可以对图像进行全方位多尺度分析，因此有利于提取织物局部表面凹凸不平的沟纹特征、织物光滑表面的图案特征和方向特征，并且Gabor变换对噪声或光照变换等外界干扰因素具有很强的鲁棒性。因此Gabor变换广泛应用于织物的疵点检测中。

1Gabor滤波的改进

Gabor滤波检测方法主要分为两大类：Gabor优化选择[6]与多通道Gabor滤波融合[7]，其中多通道Gabor滤波融合主要是采用奇数对称Gabor滤波器与偶数对称Gabor滤波器组成的滤波器组滤波，然后采用伯努利组合法则融合两个通道滤波后的图像，再进行后续处理，该方法运算量大，不具有实时性，应用于工业生产受到限制。Gabor滤波优化选择是根据一定规则从不同通道的滤波后图像中选取出最优的图像进行后续处理，该方法在保证检测正确率的前提下，能够尽可能减少运算时间，拥有很强的实时性，适用于工业生产。

其中Kumar等[8]提出了一种代价函数判断选择方法，在滤波器理想的条件下，用该滤波器分别处理带有疵点的织物图像与无缺陷的织物图像，计算滤波后图像中的像素均值，由于带有疵点的织物图像滤波后的图像中一般只含有背景区域和瑕疵区域，因此带有疵点的织物图像像素平均局部能量很高，无缺陷的织物图像像素平均局部能量很低，通过这一特点可以构建代价函数可用于实现平均局部能量的最大分离，从而在一定程度上实现优化选择。该优化选择代价函数的总体思路为：设置K个尺度，M个方向的滤波器组滤波，得到K×M幅滤波后图像，再将各幅滤波图像分割为S个独立的子块，其计算见式（1）。

求取最优滤波通道，故选择代价函数最大的通道为最优滤波通道。

虽然Kumar等提出的代价函数判断选择方法效果较为理想，但是文献[9-10]中分别指该方法不适合大面积型瑕疵的检测，分块大小的选择对优化选择的影响较大。除此之外，由于选取的单张图片具有随机性，该算法鲁棒性较差。

本研究对Kumar选择方法进行优化，为了避免产生基于单个像素级别的偏差，选取带有疵点的织物图像与无缺陷的织物图像滤波后的图像的全局偏差来实现优化选择。首先通过处理P幅标准无瑕疵图像求得各个滤波通道的标准像素值，再将第i个滤波器滤波后图像分割成S个大小的子块并求取每个子块均值，计算每幅图像中各子块像素与对应通道标准像素均值之差的平方和，并根据式（3）求取最优滤波通道。

改进后的选择方法具有计算量小的优点，削弱了的取值对优化选择的影响，通过对多幅图像的运算降低了各通道标准均值数值的偶然性，并且避免了均值比方法带来的瑕疵信息被均匀化的缺点。

2织物瑕疵检测方法的设计与实现

基于改进Kumar优化选择方法，本研究设计了一种织物疵点检测方法，主要分为4个步骤：a）对传入的图像进行预处理，凸显图像疵点特征;b）构建标准图像多通道滤波后各通道标准参数库，实现测试图像多通道滤波;c）将测试图像多通道滤波后的数据实行优化选择，二值分割等操作;d）通过统计学方法实现织物疵点检测判断。本研究设计的织物瑕疵检测方法完成过程如图1所示。

2.1图像预处理

图像预处理是为了削减混入织物图像的噪声，突出织物疵点信息，减少光照不均等环境因素带来的影响，使得织物图像便于后续的特征提取。

虽然通过图像的简单灰度数据缩放可以去除抑制环境因素带来的影响，但是削减噪声的同时也导致了疵点数据的丢失，由于收集到的图像为RGB三通道图像，其数据量较大，因此直接采用灰度数据缩放处理的方式处理图像不具有实时性，为了便于加快后续算法处理与适应程序处理中的特殊条件，将收集到的RGB三通道图像通过加权平均法转化为灰度图像。

为了将图像中的局部高带通能量区域转变为强灰度分布区域，将织物图像通过高斯滤波器进行平滑操作，因为织物图像的光谱特征与纱线密度以及织造图案密切相关，本研究处理的是不含织造图案的单色织物，高斯滤波器对于织造图案的影响仍有待研究，若织物纱线密度高其频谱具有高频成分，需要采用较小尺寸的窗口模板，相反，对于纱线密度低的织物则需要采用较大尺寸的窗口模板，试验证明将窗口模板大小设置为织物纹理的最小周期，会使平滑操作达到最佳效果。紧接着，为了将图像转换成唯一的标准形式以削减几何变换对图像带来的影响，从而突显图像中的常量，本研究将通过高斯滤波器处理后的织物图像代入式（4）、式（5）进行线性归一化处理。

式中：g（i，j）为经过高斯滤波器平滑后的图像在（i，j）处的像素值，p（i，j）为原图像在处的像素值，src（i，j）为经过初步处理后的图像在（i，j）处的像素值，min（src（x，y））表示经过初步处理后的图像中像素值的最小值，max（src（x，y））表示经过初步处理后的像素中图像像素值的最大值，min表示图像归一化所能接受的最小值，max表示图像归一化所能接受的最大值。

最后，为了使得处理后的织物图像具有较高对比度与较大动态范围，本研究采用限制对比度自适应直方图均衡化处理[11]的方法将图像像素值占有尽可能多的灰度级并均匀分布。经过图像增强处理后的测试图像如图2所示。

其中左边为测试图像，右边为图像增强后的图像，可以看出，相较于左边，右边图像中疵点部分的像素明显得到了增强。

2.2疵点识别

首先设置好一组3×4的Gabor滤波器组，其中滤波器方向为0、π3、2π3，波长设置为2、8、16、32px，尺度设置为l即织物纹理的最小周期，将多幅无疵点标准图像与测试图像先后通过设计好的滤波器组滤波，在无疵点标准图像通过滤波器组滤波处理后，求得各个通道滤波后图像的标准平均像素值

并记为E。在无疵点标准图像通过滤波器组滤波处理后，根据式（3）确定最优滤波通道，选择最优滤波图像。

在最优滤波图像中的疵点区域与常规织物区域存在较大的能量差，根据这一特点本研究采用二值分割的方式区分疵点区域与常规织物区域，在最优滤波图像中大于阈值k的部分将被认定为疵点部分，小于阈值k的部分将被认为常规织物部分，阈值的选定直接决定了二值分割的效果，为了提高系统的鲁棒性，增加阈值的灵活性与适应性，采用大津算法[12]实现动态阈值分割。

最后经过形态学处理，将疵点部分特征放大，并消除部分噪声的干扰。在通过实际测量261张不同种类的疵点图像与正常图像经过处理后黑白像素比重，设置测试图像经过处理后白色像素点占比大于0.04%的为疵点图像，如图3所示，本研究设计的方法能够精准地识别样本中是否含有疵点，并可以对疵点进行定位。

3结果与分析

实验计算机硬件环境：处理器为Intel（R）Corei5-7300HQCPU（2.50GHz）、内存16GB、图形处理器NVIDIAGeForceGTX1050Ti（4G）。使用Python语言进行编程，对标称规格为4444（经密44根/cm、纬密44根/cm），组织循环数为2的织物进行图像采集，采集的织物图像均采用JPG格式，最终的样本图像尺寸均为2448像素1200像素，织物纹理最小周期为5像素。采集的样本图像中共包含18类疵点，疵点类型包括擦伤、空织、油污、斷纬、断经、紧边、色点、竹节、停车挡、色差、多复合疵点等，为了评价方法实际应用时的检测效果，通过检测1538张图像并根据式（6）、式（7）、式（8）、式（9）分别求得准确率、查准率、特异性、召回率。

式中：TP为被正确地划分为正例的样本数，FP为被错误地划分为正例的样本数，FN为被错误地划分为负例的样本数，TN为被正确地划分为负例的个数。准确率用于评估模型的全局精准程度。查准率又称为精准率，用于描述在预测为正例的样本中实际为正例样本的比例。特异性用于描述在实际为负例的样本中预测为负例样本的比例。召回率又称为查全率，用于描述在实际为正例的样本中预测为正例的比例。

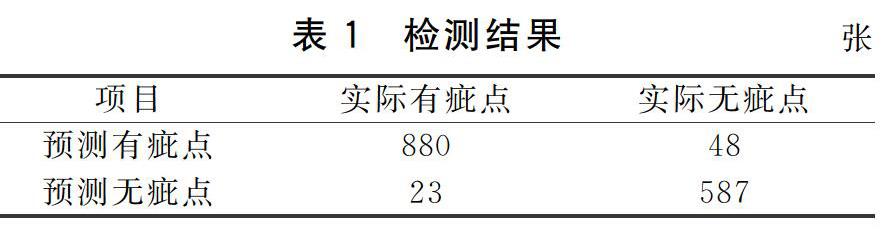
得出结果：判断有无疵点的准确率为95.38%，查准率为94.82%，特异性为92.44%，召回率为97.45%。检测结果如表1所示。

本研究重点分析了误检图像，在预测有疵点但是实际无疵点的图像中，含有织物褶皱的图像占比高达72.9%，通过查看过程处理结果本研究发现因为织物褶皱导致图像像素点分布不均匀，导致图像含有油污疵点的部分特征，采用该方法识别易将褶皱识别为大面积疵点。在预测无疵点但是实际有疵点的图像中，不明显的断经断纬疵点、停车挡、色差等疵点占比较小或不明显的图像，采用本研究方法识别易将疵点图像识别为标准图像。预测有疵点实际无疵点的误检图像分析如表2所示，被误检的图像经过本研究方法的结果如图4所示。

4结语

本研究设计了一种织物瑕疵检测方法，首先对图像进行增强，后将图像通过Gabor滤波分解，根据代价函数在子图像中分拣出最优滤波子图像，继而采用形态学与统计学操作最终较好地满足疵点识别的需求。该方法针对破洞、油污、复合瑕疵等疵点具有很好的识别能力，对褶皱、不明显的断经、断纬、色差等疵点识别能力偏弱。本研究设计的方法只能提供有无疵点的二元判断，不能将疵点进行详细分类，因此降低褶皱等疵点误检，疵点类型分类与识别是下一步的研究重点。

参考文献：

[1]李文羽，程隆棣.基于机器视觉和图像处理的织物疵点检测研究新进展[J].纺织学报，2014，35（3）：158-164.

[2]NGANHYT，PANGGKH，YUNGNHC.Motif-baseddefectdetectionforpatternedfabric[J].PatternRecognition，2008，41（6）：1878-1894.

[3]AURAC，CLAUDIABP.Afractalimageanalysissystemforfabricinspectionbasedonabox-countingmethod[J].ComputerNetworksandISDNSystems，1998，30（20）：1887-1895.

[4]BODNAROVAA，BENNAMOUNM，KUBIKK.DefectdetectionintextilematerialsbasedonaspectsoftheHVS[C]//ProcSMC.SanDiego，CA：IEEEPress，1998：4423-4428.

[5]GABORD.Theoryofcommunication[J].IeeProcLondon，1946，93（73）：58.

[6]MAKKL，PENGP.AnautomatedinspectionsystemfortextilefabricsbasedonGaborfilters[J].RoboticsandComputerIntegratedManufacturing，2008，24（3）：359-369.

[7]何薇，白瑞林，李新.基于Gabor小波和神经网络的布匹瑕疵检测[J].計算机工程与应用，2016，52（12）：231-234.

[8]KUMARA，PANGGKH.DefectdetectionintexturedmaterialsusingGaborfilters[J].IEEETransactionsonIndustryApplications，2002，38（2）：425-440.

[9]李益红，卢朝阳，李静，等.一种新的Gabor优化选择检测算法及应用[J].计算机工程与应用，2012，48（5）：4-6，11.

[10]赵宏威，王亦红.基于改进Gabor优化选择的布匹瑕疵检测方法[J].计算机工程与应用，2019，55（24）：202-207.

[11]刘德全，崔涛，杨雅宁.局部对比度自适应直方图均衡化图像增强的算法研究[J].信息与电脑（理论版），2016（7）：79-80.

[12]李了了，邓善熙，丁兴号.基于大津法的图像分块二值化算法[J].微计算机信息，2005（14）：76-77.