地球电子外辐射带的数据同化建模与分析

朱佳楠， 郭建广 ， 倪彬彬， 曹兴， 项正，付松， 顾旭东， 马新

1 武汉大学电子信息学院空间物理系, 武汉 430072 2 中国科学院比较行星学卓越创新中心, 合肥 230026 3 中国气象局国家空间天气监测预警中心, 北京 100081

0 引言

地球辐射带由地球磁场捕获的高能带电粒子构成，被槽区分割为内辐射带和外辐射带.其中内辐射带(距地心1.1～2.5RE)主要由质子组成，其通量水平相对稳定，外辐射带(距地心3～8RE)主要由电子组成，其通量呈现着复杂、剧烈的动态演化特征.由于外辐射带中高能电子对卫星仪器和宇航员健康存在潜在威胁，研究辐射带电子的分布与演化过程有着十分重要的意义.

辐射带电子的分布和演化与磁暴发生关系密切.Reeves等(2003)通过分析1989—2000年期间276个磁暴事件得出，磁暴可以增加或减少辐射带相对论电子的通量，也会使电子通量保持不变.电子通量的变化过程是电子输运、加速和损失过程的平衡.由ULF波驱动的向内的径向扩散被认为是电子加速的重要机制(Ozeke et al., 2012, 2014)，向外的径向扩散则造成电子损失(Shprits et al., 2008; Bortnik et al., 2006).波粒相互作用引起的能量和投掷角扩散也能够有效地加速和损失电子(Meredith et al., 2002; Horne et al., 2005; Thorne et al., 2005; Cao et al., 2019; Ma et al., 2020).一系列研究表明，合声波既可以加速电子也能导致电子的散射损失(Summers et al., 2007a,b; Thorne et al., 2007, 2013)，嘶声波通过投掷角散射可损失几十千到几兆电子伏特的电子(Meredith et al., 2007, 2009; Baker et al., 2007; Ni et al., 2013; Cao et al., 2017, 2020).

研究辐射带电子相空间密度(Phase Space Density，简记为PSD)分布可以分析潜在的电子动态变化机制(Xiang et al., 2017, 2018; 刘泽源等, 2020).但是卫星观测受限于轨道的时空位置和有限的投掷角、能量范围.模拟辐射带的物理模型存在计算方程简化处理、初值和边界值难以确定等不足.数据同化技术将有限的卫星观测与物理模型结合起来，得到辐射带电子分布的最佳估计.

Naehr和Toffoletto等(2005)首先将基于卡尔曼滤波的数据同化方法使用于辐射带粒子分布的模拟与预测上，验证了该方法的可行性.Koller等(2007)、Shprits等(2007)、Kondrashov等(2007)的工作进一步表明，利用数据同化方法可以准确地再现辐射带电子PSD分布.后续的工作丰富了数据同化方法，Ni等(2009a)表明同化过程中使用多个卫星的观测数据较使用单个卫星误差更小，并发现同化结果对于磁场模型的选择相对不敏感(Ni et al., 2009b).Daae等(2011)研究了边界条件和损耗模型，表明卡尔曼滤波对各种模型参数都具有鲁棒性.使用上述只考虑径向扩散的同化模型，Shprits(2012)和Ni等(2013)细致分析了辐射带电子的动态变化过程.考虑径向扩散、投掷角扩散、能量扩散的三维同化模型也被运用于辐射带研究工作中，并在此基础上提出了集成卡尔曼滤波(Bourdarie and Maget, 2012)、分裂算子卡尔曼滤波等方法(Shprits et al., 2013; Kellerman et al., 2014).数据同化中一个重要的研究对象是新息矢量，它是同化过程中观测对物理模型修改程度的度量.Shprits等(2012)利用新息矢量进行统计分析，发现槽区存在局部加速机制.Cervantes等(2020)通过对比各种损失机制下的新息矢量，得出了不同损失机制的作用范围及其与地磁活动间的关系.

本文首先利用范艾伦A星、B星GOES-13、GOES-15四颗卫星的数据对2013年3月的辐射带电子通量进行了同化分析，细致对比了一维、二维、三维不同辐射带物理模型下的同化结果，并利用三维同化模型重现了2013年一整年电子PSD的长期演化.通过分析同化过程中的新息矢量，本文进一步讨论了所使用同化模型的性能.

1 同化方法与数据

1.1 卫星观测数据

本文使用了范艾伦双星和GOES-13、GOES-15四颗卫星2013年一整年的辐射带电子观测数据.需将卫星电子通量数据在相空间坐标(μ,K,L*)下转换为PSD作为同化过程的输入，转化过程借鉴了Ni等(2009a)的方法.并参考Kellerman等(2014)的工作，使用PSD匹配算法对来自不同卫星的观测数据进行相互校准.

范艾伦卫星包括A星、B星两颗运行轨道和携带仪器完全相同的卫星，其轨道倾角约10°，近地点高度约1.1RE，远地点为约5.9RE，运行轨道周期约9 h.本研究使用范艾伦卫星搭载的高能粒子、成分分析与热等离子体(ECT, Energetic Particle, Composition, and Thermal Plasma)科学探测单元，其中磁化电子离子分光仪(MagEIS, The Magnetic Electron Ion Spectrometer)提供了能量范围约10 keV～4 MeV的电子通量数据，相对论电子质子探测器(REPT, Relativistic Electron Proton Telescope)提供了能量范围约1.8～20 MeV的粒子数据.卫星投掷角分布在均匀网格中插值，步长为5°.GOES系列卫星为一系列地球同步轨道卫星，用于对近地空间气象学和空间天气的监测.本研究使用了GOES-13和GOES-15两颗卫星的数据，其上搭载的粒子辐射探测仪器EPEAD(Energetic Proton, Electron, and Alpha Detector)可用于探测0.6～4 MeV的电子，MAGED(MAGnetospheric Electron Detector)用于探测30～600 keV的电子.

1.2 辐射带扩散模型

借鉴Shprits等(2008)和Subbotin(2010)等的工作，本文使用VERB-3D程序，通过求解三维Fokker-Planck扩散方程模拟电子PSD的演化，三维Fokker-Planck扩散方程的表达式为

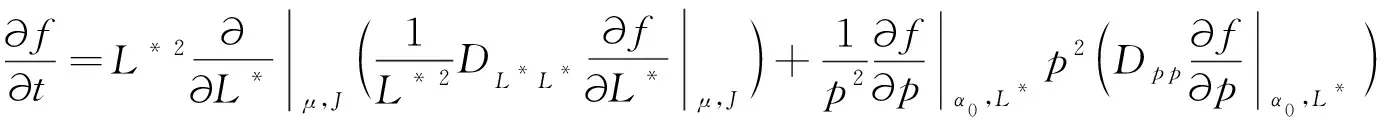
(1)

其中f表示电子PSD；μ为第一绝热不变量，与电子的回旋运动有关；J为第二绝热不变量，与电子的弹跳运动有关；L*与第三绝热不变量Φ成反比关系，沿粒子漂移路径保持不变；DL*L*、Dp p、Dα α分别是弹跳平均下径向、能量和投掷角扩散系数；T(α0)为与粒子弹跳频率有关的函数.

求解Fokker-Planck扩散方程需要已知扩散系数.参照Brautigam和Albert(2000)的方法，径向扩散系数表示为与Kp指数相关的函数.本研究只考虑嘶声波和合声波引起的电子散射，使用FDC程序(Full Diffusion Code)计算得到(Ni et al., 2008, 2015; Shprits et al., 2009; Cao et al., 2016, 2020)电子投掷角扩散和能量扩散系数，用以量化磁层波动对辐射带电子的影响.

1.3 卡尔曼滤波和新息矢量

卡尔曼滤波是一种对线性系统状态量进行最小方差无偏估计的算法，被用于数据同化过程.假设模型和观测误差是无偏的，且服从高斯分布.在更新时刻，卡尔曼滤波对当前时刻的观测值和扩散模型的预测值进行比较，在知道前一时刻分析误差和前一时刻模型误差的情况下最优地估计出当前时刻的预测误差，从而对预测值进行调整.卡尔曼滤波的计算方法如下：

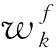
(2)

(3)

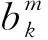
(4)

国际文凭(International Baccalaureate， IB)是由国际文凭组织(International Baccalaureate Organization， IBO)推出的课程和考试项目，大学预科国际文凭课程(Diploma Program， DP)则是面向全球16～19岁优秀高中生开展的课程[1]。IBDP生物学课程的总体特色是“轻知识、重技能”，强调实验教学的过程性和方法，旨在关注学生知识的生成过程，培养学生解决问题的能力，全方面提高生物学素养，在情感教育上则充分体现了以人为本、尊重生命的课程目标。

(5)

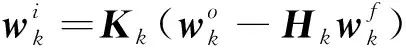
与三维Fokker-Planck扩散方程相对应，本文将考虑一种、两种及三种扩散机制的辐射带物理模型描述为一维、二维、三维扩散模型.三组辐射带扩散模型的计算结果被用做本文同化过程的输入，分别为一维纯径向扩散模型，二维径向扩散加投掷角扩散模型，三维径向扩散、投掷角扩散加能量扩散模型.经过卡尔曼滤波的同化处理，分别对应了下文所述的一维、二维、三维同化模型.

2 同化结果与分析

2.1 2013年3月不同扩散模型下辐射带电子通量的同化结果

采用上述数据同化的方法，本文首先计算了2013年3月辐射带电子通量的观测及多维同化结果，如图1所示.同化过程中设定的观测误差和模型误差均为0.5，即观测误差与模型误差的比值为100%.图1a展示了在L*=3～7范围内Ek=0.6 MeV，αeq=30°电子通量的卫星观测结果.图1b—d展示了该能量和投掷角下一维、二维、三维不同扩散模型的同化结果.与上述类似，图1e—h展示了Ek=1 MeV，αeq=55°电子通量的卫星观测及同化结果.图1i给出了该时间段内Kp和Dst指数的变化情况.图中的黑线表示由Carpenter和Anderson(1992)模型计算得到的等离子体层顶位置.如Kp指数所示，3月1日和3月17日分别发生了两次磁暴，其中3月17日的磁暴较强.图1a的观测结果显示，磁暴主相期间辐射带电子通量快速损失，在恢复相通量有所增强并形成峰值.图1b—d所示三组不同扩散模型下的同化结果均模拟出了磁暴前后电子通量的变化过程，且填补了L*=5.5附近和L*>6.5时观测值的空缺，较为精确地重现了辐射带电子通量的径向分布.图1e—h所示Ek=1 MeV，αeq=60°电子的通量值略小于Ek=0.6 MeV，αeq=30°的电子通量值，同化模型在该能量和投掷角下也可以模拟出电子通量的分布和变化.

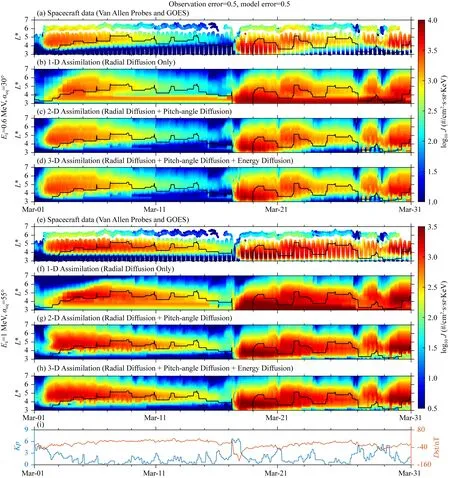
图1 设定观测误差和模型误差均为0.5时，2013年3月辐射带电子通量的观测结果和一维、二维、三维不同辐射带扩散模型下随时间和L*分布变化的同化结果.(a—d) 对应Ek=0.6 MeV，αeq=30°的辐射带电子； (e—h) 对应Ek=1 MeV，αeq=55°的辐射带电子； (i) Kp和Dst地磁指数随时间的变化.(a—h)中黑线表示等离子体层顶位置Fig.1 For the case that both the observation error and model error are 100%, observations of radiation belt electron fluxes and the corresponding data assimilation results using the 1-D, 2-D and 3-D radiation belt diffusion models over the month of March 2013 for radiation belt electrons with (a—d) Ek= 0.6 MeV, αeq=30° and (e—h) Ek=1 MeV, αeq=55°. (i) The time series of Kp and Dst indices. Black curves in (a—h) show the plasmapause location

为进一步展示采用不同维度扩散模型对同化结果的影响，我们在图1结果的基础上重新设置观测误差为1，模型误差为0.5，即观测误差与模型误差的比值为200%，其余参数与图1相同，结果如图2所示.需要说明的是，观测误差与模型误差的比值越大，同化结果越忽视观测对扩散模型的修改，而更关注扩散模型本身的模拟效果.由图2所示同化结果可以看出，磁暴发生前后电子通量的变化趋势与图1基本一致，但三组扩散模型的模拟效果表现出明显的差异.与观测相比，图2b和图2f所示的一维同化结果在磁暴主相期间高L*区域的电子通量值远小于观测值，在磁平静期低L*的电子通量远高于观测值.二维扩散模型在纯径向扩散的基础上加入了投掷角扩散，可以从图2c和和2g所示的同化结果观察到低L*电子的显著损失，即嘶声波可以对等离子体层顶以内的辐射带电子有效散射.图2d和图2h在二维扩散模型的基础上加入了能量扩散，可以在L*>4的区域观察到磁暴后电子通量的迅速增加，即在等离子体层顶以外合声波能对辐射带电子有效加速.对比三组维度扩散模型下的同化结果，三维同化模型提供了有效的加速和损失机制，其同化结果能最优地模拟出辐射带电子通量的径向分布.

图2 同图1类似，但是设定观测误差为1，模型误差为0.5Fig.2 Same as in Figure 1, except for the setting that the observation error is 1 and the model error is 0.5

对应于图1和图2，图3展示了不同维度扩散模型下的同化结果在不同L*的模拟效果.从左至右对应两组能量和投掷角，从上至下对应两组观测和模型误差，子图自上而下分别为L*= 4、5、6时电子通量的观测和三组同化结果随时间的变化.与图1、图2的结论一致，L*= 4时，一维同化结果在3月1日磁暴后的磁平静期高于观测结果，L*= 5、6时，一维、二维同化结果在磁暴后均低于观测结果.三维同化结果在两组能量、投掷角和三组L*下均与观测结果很好地吻合，有效修正了一维和二维同化结果的误差，说明除了径向扩散和投掷角扩散，能量扩散对辐射带电子演化也发挥着重要作用.还可以看出，三组同化结果与观测的吻合度随时间的推移变高，由于同化过程会在每个时间步长更新误差矩阵，同化的时间越长模型的同化效果越好.

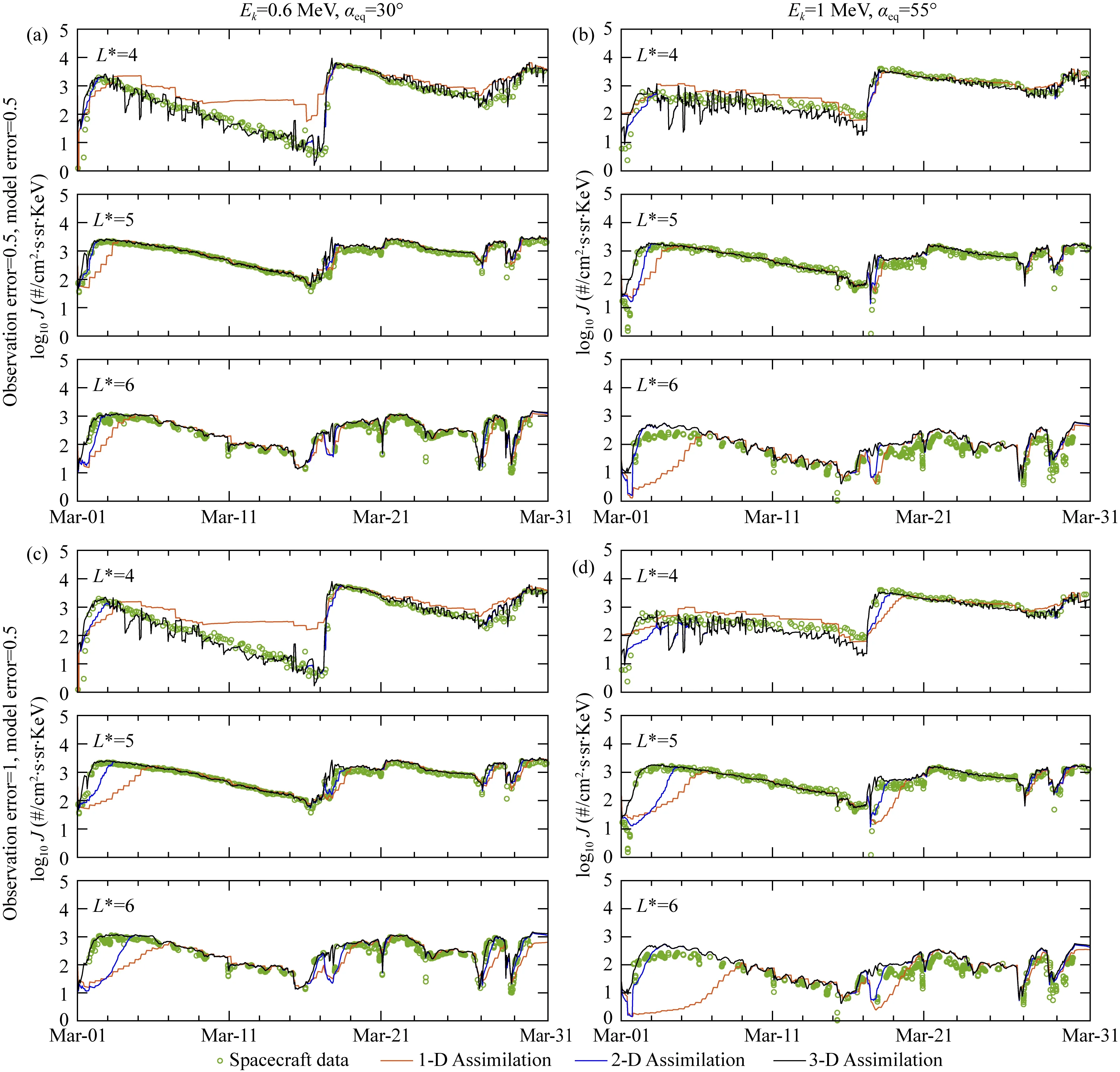
图3 对应于图1和图2，当L*=4、5、6时，辐射带电子通量的观测和不同维度辐射带扩散模型下的同化结果的比较Fig.3 Corresponding to Figures 1 and 2, comparisons between the observations of radiation belt electron fluxes and the assimilation results in March 2013 for the indicated two at L*=4, 5 and 6

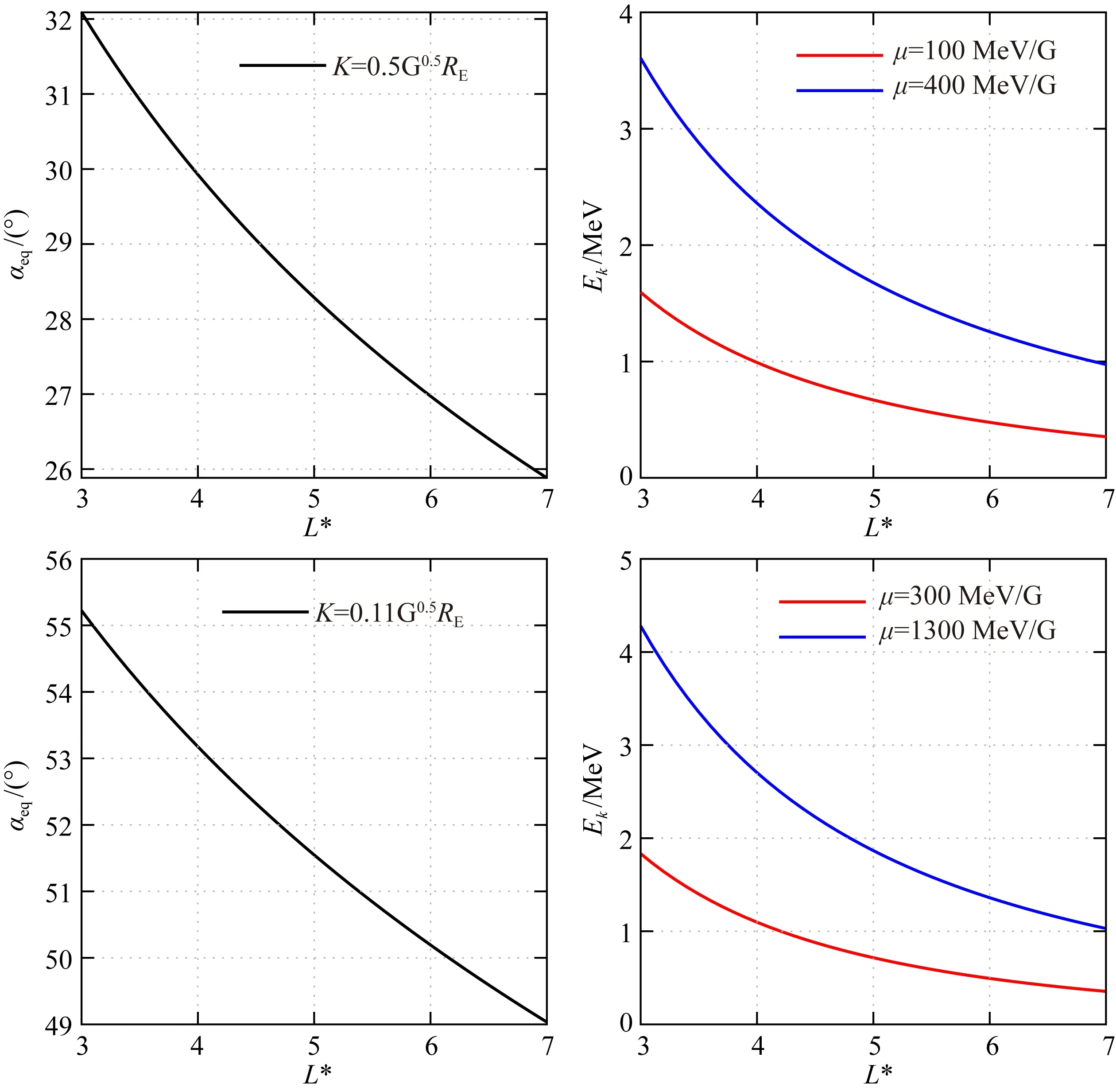
图4 偶极地磁场下绝热不变量K、μ与赤道投掷角αeq、电子能量Ek随L*的对应关系Fig.4 Dependence of equatorial pitch angle and electron kinetic energy on L* in a dipole geomagnetic field for the indicated four pairs of (K, μ)

增大观测误差与模型误差的比值可以展示不同维度扩散模型下同化结果的显著差异，减小观测误差与模型误差的比值可以得到与观测更为吻合的同化模型.通过一系列测试，当观测误差与模型误差均为0.5时，三维同化结果已经可以精确地重现辐射带电子的分布和变化.

2.2 2013年全年辐射带电子PSD的同化结果分析

为了展示三维辐射带同化模型对较长时间辐射带电子动态演变的模拟效果，本文对2013年一整年辐射带电子PSD进行了同化分析.通过研究以三个绝热不变量(μ,K,L*)构成相空间坐标系下电子PSD的长期演化，可以区分非绝热效应和绝热效应、局部加速和径向传输过程，有助于理解辐射带电子加速、输运和损耗过程之间的平衡.如章节1.2所述，μ是第一绝热不变量；第二绝热不变量J通常用K来代替，K只与背景磁场的强度和结构有关，与带电粒子质量和电荷数无关.我们选取两组固定K值下不同μ值的四个有代表性的绝热不变量结果进行分析，其中第一组为K=0.5 G0.5RE，μ=100 MeV/G和μ=400 MeV/G，第二组为K=0.11 G0.5RE，μ=300 MeV/G和μ=1300 MeV/G，偶极磁场下它们与αeq和Ek随L*的对应关系如图4所示.通过选取这四组绝热不变量，可以获得在较高和较低投掷角、较大能量范围下的电子PSD.

图5 设定K=0.5 G0.5RE，2013年全年辐射带电子相空间密度随L*和时间分布的观测和三维同化结果(a—b) 对应μ=100 MeV/G的辐射带电子； (c—d) 对应μ=400 MeV/G的辐射带电子； (e) 地磁指数Kp和Dst.(a—d)中黑线表示等离子体层顶位置.Fig.5 For the case that K=0.5 G0.5RE, observations of radiation belt electron PSD and the corresponding data assimilation results using 3-D radiation belt diffusion models during 2013 with (a—b) μ=100 MeV/G and (c—d) μ=400 MeV/G. (e) Kp and Dst indices. Black curves in (a—d) show the plasmapause location

同图5类似，图6显示了设定K=0.11 G0.5RE，μ=300 MeV/G和μ=1300 MeV/G时辐射带电子PSD的观测和同化结果.电子的投掷角更高，其PSD值也更高，但PSD的变化趋势基本不变.在该组绝热不变量下，三维同化结果仍可以很好地模拟出电子PSD的径向分布和长期演化过程.四组绝热不变量下的同化结果表明，磁暴造成的电子PSD损失与增加可以发生在广泛的能量和投掷角范围中.

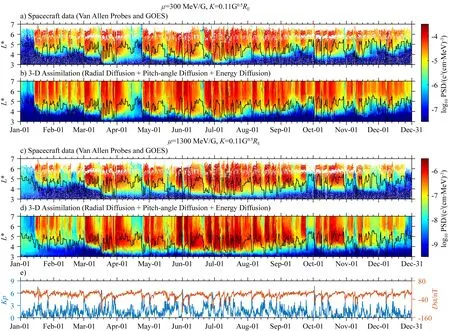
图6 同图5类似，但设置K=0.11 G0.5RE，μ=300 MeV/G和μ=1300 MeV/GFig.6 Same as in Fig.5, except for the setting that K=0.11 G0.5RE, μ=300 MeV/G and μ=1300 MeV/G

本文计算了2013年一整年的平均新息矢量，结果如图7所示：从左至右分别代表三个不同维度的同化模型，从上至下对应不同的μ、K.如章节1.3所述，新息矢量反映了同化过程在多大程度上修改了模拟值，新息矢量为正(负)值表示卫星观测值大于(小于)扩散模型模拟值，即模拟值与观测值相比缺少了一些加速(损失)机制，同化过程通过从模拟值中加入(减去)附加PSD值修正模拟值与观测值之间的误差.新息矢量还可以作为模型中电子损耗与源的指标，当模型中加入不同扩散机制后，同一绝热不变量条件下的新息矢量由正值变为负值，表明模型加入了有效的加速机制；新息矢量由负值变为正值，表明加入了有效的损失机制.

从图7可以看出，一维同化结果的新息矢量在L*>5.8的区域为正，在低L*趋于零，同化过程未对模型值有效修正.比较一维和二维的结果，L*=4～5的新息矢量由趋于零变为正，模型中加入了损失机制，表明投掷角扩散对电子有效损耗；比较二维和三维的结果，L*>5.2的新息矢量由正变为负，模型中加入了加速机制，表明能量扩散对电子有效加速.三维同化结果的新息矢量在L*=4～5为正，即观测值高于模拟值，因此同化过程在模拟值上加入了一定PSD；新息矢量在L*>5.2为负，观测值低于模拟值，因此同化过程从模拟值中减去了一定PSD.观测值与模型之间的误差表明本文数值模拟阶段使用的波动经验模型可能不够精确，加入了过多的损失和加速，也可能是模拟过程中忽略了一些物理机制.高L*处三维同化结果的新息矢量值随着Kp指数增大而增大，说明同化过程在地磁活动剧烈时对模型值的修正更多，此时波动经验模型的模拟效果较差.

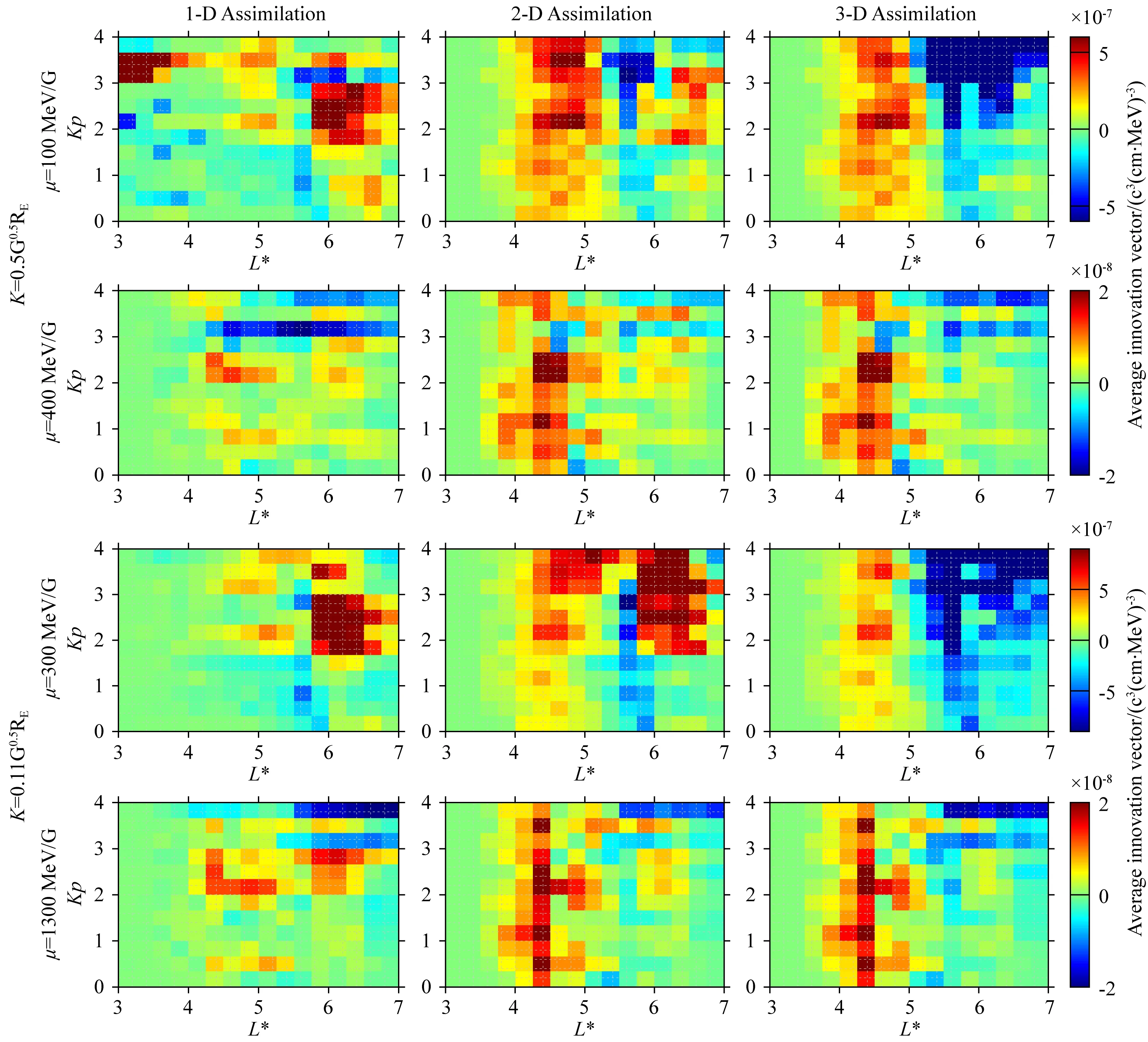
图7 2013年一整年的平均新息矢量，横坐标为L*，纵坐标为Kp指数.从左至右：一维、二维、三维扩散模型.从上至下：K=0.5 G0.5RE，μ=200 MeV/G和400 MeV/G；K=0.11 G0.5RE，μ=300 MeV/G和1300 MeV/G.Fig.7 For the indicated adiabatic invariants (K=0.5 G0.5RE, μ=200 MeV/G and 400 MeV/G; K=0.11 G0.5RE, μ=300 MeV/G and 1300 MeV/G), average innovation vector as a function of L* and Kp using the 1-D, 2-D and 3-D radiation belt diffusion models.

3 总结与讨论

本文使用了基于卡尔曼滤波的数据同化方法，将范艾伦A、B星和GOES-13、GOES-15四颗卫星的观测数据与不同维度的辐射带物理模型相结合，重构了2013年外辐射带电子的径向分布和时空演化过程，得到以下主要结论：

(1) 与一维纯径向扩散数值模型和二维径向扩散加投掷角扩散数值模型相比，加入了能量扩散的三维数值模型下的数据同化结果与卫星观测结果的吻合度最好，这说明在外辐射带电子动力学变化过程中，除了径向扩散和投掷角扩散，能量扩散对电子的加速过程也发挥着重要作用.

(2) 通过对不同绝热不变量组合的同化模拟，发现三维辐射带同化模型可以合理地获取L*=3～7范围内的地球外辐射带不同投掷角、不同能量上的电子相空间密度分布，能填补现有观测数据在空间分布上的不足，提供电子相空间的完整径向分布.

(3)随着地磁活动的变化，三维辐射带同化模型较好地重构了外辐射带电子长期的动态演化过程.同化结果表明，电子相空间密度的时空变化与磁暴事件具有很强的依赖性：磁暴主相期间会经常发生电子相空间密度在大多数L*上的快速降低，而在磁暴恢复相期间电子相空间密度一般会增强并达到峰值.

(4)通过分析同化过程中的新息矢量，可以看出辐射带物理模型常在低L*处低估观测值而在高L*处高估观测值.这些差异可能由物理模型中考虑的波动模型不完善造成，也可能由模拟过程中一些物理机制的缺失引起.新息矢量的数值随地磁活动增强而增大，说明本文采用的辐射带物理模型在磁扰期的模拟效果与地磁平静期相比不确定性增加，有待进一步深入研究.

综上，本文开展的地球电子辐射带三维数据同化建模具有有效、合理重构外辐射带电子的径向分布以及长期时空演化过程的能力.我们会在后续的研究中依据新息矢量提供的重要信息对模型加以改进，包括建立更加真实合理的磁层波动全球分布模型、考虑波动对辐射带电子的混合扩散机制以及加入更多卫星数据到同化过程.我们希望通过多维度数据同化的方法获取关于地球辐射带动态变化的更多详细信息，进一步加深对近地空间粒子辐射环境动力学过程与机制的理解认知，服务于空间天气过程与效应的预测预报.

致谢感谢范艾伦卫星团队提供数据.范艾伦卫星电子通量数据来源于(https:∥www. rbsp-ect. lanl.gov/data_pub).地磁活动指数来自NASA OMNIWEB (https:∥omniweb. gsfc. nasa. gov).感谢德国地学研究中心(GFZ)Yuri Shprits教授给予的帮助.