概率密度匹配方法在我国近海海面10 m风速预报中的应用

胡海川，赵伟, 董林

(国家气象中心，北京100081)

1 引 言

随着数值模式的不断发展，各气象要素的预报效果有了明显的提升，但由于模式的动力框架、物理参数化、初始场误差等因素的影响，数值模式存在着不可避免的系统性误差，各要素的预报与实况观测仍有一定差距[1]。对于模式的预报问题，初始场的质量无疑是至关重要的，其生成是以气象观测提供的数据和信息为基础[2]。海上资料严重缺乏，无论海面还是高空资料都很稀少，这给构建高质量的初始场造成了很大的困难[3]，使得数值模式难以对海上气象要素进行准确刻画。海面风速直接影响航运安全及海上生产作业，因此需要对数值模式的预报结果进行后处理，以进一步提升10 m 风的预报效果。常用的风速订正方法以统计学方法为主，包括传统的统计学方法及机器学习方法，通过建立实况观测数据与数值模式预报的数学模型，实现对风速的客观订正[4]。相比于陆地开展的风速订正工作[5-12]，受限于海上观测资料的稀缺及卫星反演的洋面风场数据的较大误差[13-15]，海上风速订正工作开展的相对较少，且多集中在沿岸、海岛或近海小范围海域。陈德花等[16]利用BP 神经网络方法对MM5 模式在福建沿海站点的风速预报进行订正，经订正后的风速预报较订正前有一定改善，特别是对大风(>10 m/s)的预报能力提升明显。胡波等[17]利用高斯回归方法建立阵风与气象要素的概率模型，实现对浙江沿海海岛的阵风预报。李辉等[18]利用港湾码头的小时极大风观测数据与热带气旋特性因素建立预报模型，进行重点区域的最大阵风值预报。王亚男等[19]、荣艳敏等[20]分别利用递减平均法及MOS方法开展了渤海及山东近海的风速预报工作。随着国家综合实力的全面提升，海洋气象服务需求的不断加大，仅针对沿岸、海岛或小范围海域的风速订正已不能满足需求，应进一步提升海上大风预报准确率及服务能力，开展基于海表面风场预报的客观订正工作。海洋下垫面相对均一，在一定程度上降低了风速订正的难度，为海面风速订正提供了有力基础。胡海川等[21-22]利用我国沿海代表站点观测数据对集合预报海面10 m 风速预报产品及极大风预报产品进行误差检验分析，并将误差适用于我国近海海域，实现对海面10 m 风速及极大风的客观订正。上述方法只能针对分辨率相对较低的集合预报进行，在集合预报成员众多信息量大的特性基础上开展订正工作，并不能适用于分辨率较高的确定性模式。本文将采用相同思路，在我国沿海代表站观测数据的基础上，利用概率密度匹配方法对确定性模式海面10 m 风速预报的系统性误差进行订正。

概率密度匹配方法是通过调整模式结果，使其与实况观测的概率密度分布一致，从而实现订正。该方法计算简单，在系统误差的订正方面具有较好效果，且不必分析资料产生系统误差的复杂来源，因而被广泛应用在模式降水及卫星观测等资料的订正中[23-27]。造成我国近海大风天气过程的天气系统主要可分为冷空气型、温带气旋型和热带气旋型，其中冷空气型又包括小槽东移型、小槽发展型和横槽转竖型；温带气旋又包括东海气旋型、黄渤海气旋型和蒙古气旋型[28]。模式对于不同天气系统的预报误差不同，而概率密度匹配方法不必分析复杂的误差来源，可更好地适用于资料稀少且影响系统复杂的海面风速订正上。钱磊等[29]已基于概率密度匹配方法对安徽省地区开展了WRF 模式的阵风订正工作，当实况风速大于6级时，经概率密度匹配方法订正后的结果与实况较一致。本文将利用概率密度匹配方法开展我国近海海面10 m 风速的订正工作，利用该方法的优势，提升数值模式对海上大风预报的准确率。

2 资 料

本文利用2017—2019年ECMWF确定性模式的10 m 风场预报数据及地面实况观测数据，ECMWF 数据空间分辨率为0.25 °×0.25 °，预报时效为12～120 h，间隔12 h。选取我国沿岸及近海88 个观测站点作为代表站，分布如图1 所示。2017—2018年的数值模式及地面观测数据用于模式风速预报误差的分析与订正系数的求解，2019年数据用于订正效果的验证。文中所选取的代表站点基本覆盖我国东部沿岸和近海区域，求解出的订正系数可适用于我国近海。在计算数值模式10 m 风速误差时将所有站点进行统一计算，且所选取站点平均海拔高度为21 m，因此未进行实况风速的高度订正。

图1 沿岸及近海代表站点分布

3 预报误差

图2 为2017—2018 年ECMWF 确定性模式10 m风场预报的平均偏差，对于实况出现8 m/s以下风速，模式在各个时效的平均误差均表现为正偏差。对于实况出现8 m/s以上风速，模式表现为负偏差，且随风速增大、预报时效的延长，负偏差程度显著增加。在24 h 预报中，模式对于实况出现8～10 m/s 风速预报的平均误差为-0.4 m/s，18～20 m/s 风速预报的平均误差为-4.5 m/s。在120 h 预报中，模式对于实况出现8～10 m/s 风速预报的平均误差为-1.1 m/s，18～20 m/s 风速预报的平均误差达-6.0 m/s。

观测实况中，8 m/s 以下风速的样本量较大，但模式对于8 m/s 以下风速的预报较实况观测略有偏大。在图3的散点图中可看出，各个预报时效中，实况出现8 m/s以下风速时的散点集中分布在对角线左侧。实况出现8 m/s以上风速时，散点更多地分布在对角线右侧，随着预报时效的延长，对角线右侧分布的散点数量明显增加。综上，数值模式10 m 风速预报存在明显的小风预报偏大、大风预报明显偏小的误差特点。

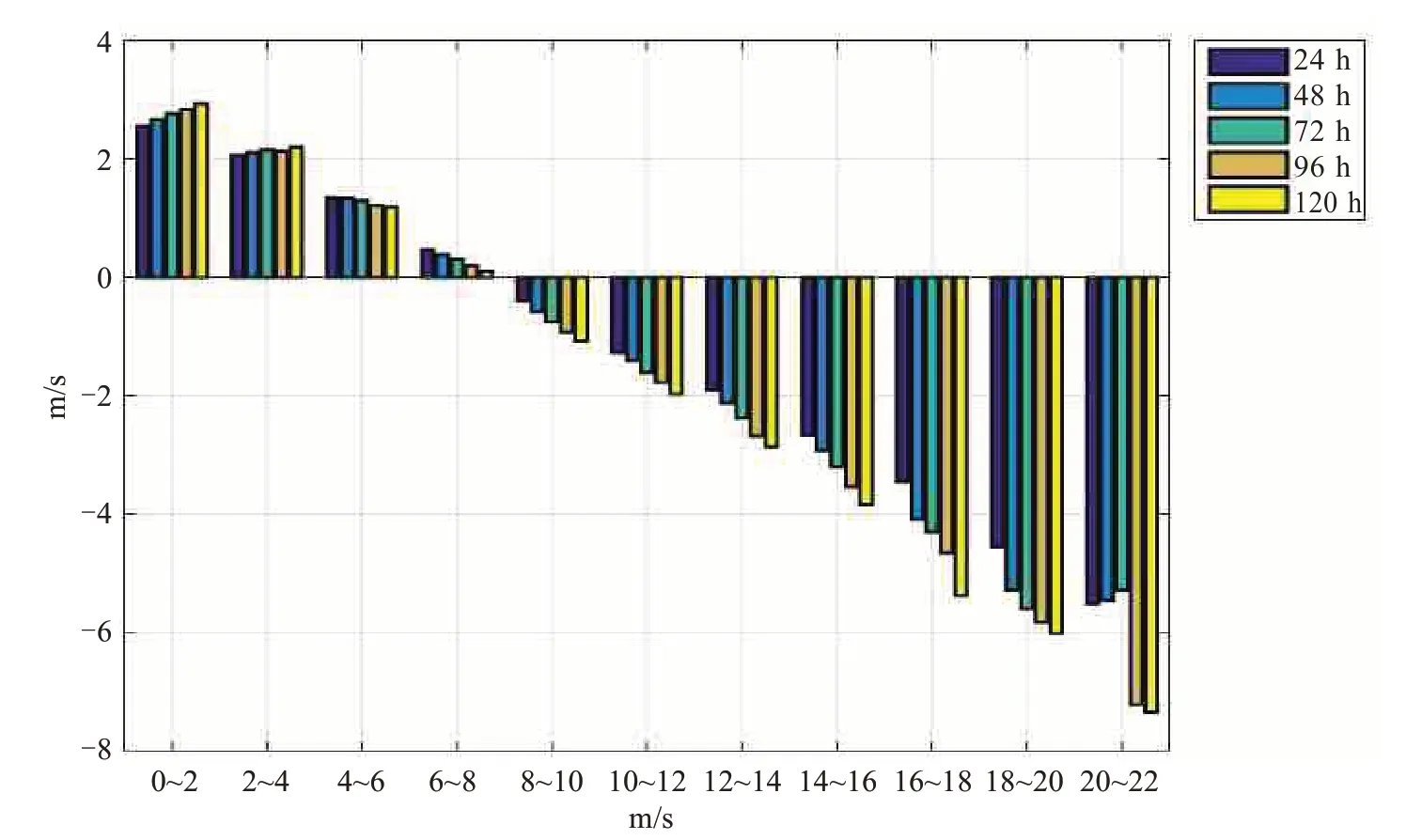
图2 2017—2018年ECMWF模式10 m风速预报平均偏差

图3 2017—2018年ECMWF模式10 m风速预报散点图 a. 24 h预报；b. 48 h预报；c. 72 h预报；d. 96 h预报。

针对数值模式10 m 风速预报所表现出的“小风大、大风小”特点，计算实况观测及模式预报数据出现不同风速阈值时频次，计算公式如下：

式中，Ai为出现某一量级风速阈值的站点次数，B为总站次，Pi为出现某一风速阈值的频率。如图4a所示，对于小量级风速，数值模式预报的频率略高于实况出现的频率，因而造成数值模式对于小量级风速预报偏大；对于大量级风速(图4b)，数值模式预报的频率明显低于实况出现的频率，因而出现模式对大量级风速预报明显偏小的情况。利用概率密度匹配方法将数值模式对于不同风速阈值预报的频率进行有效的调整，使其趋于实况观测的频率，以改善“小风大、大风小”的误差特性，提高其预报准确率。

图4 2017—2018年ECMWF模式10 m风速预报与风速实况观测频率对比 a. 2～8 m/s风速频率对比；b. 12～18 m/s风速频率对比。

4 概率密度匹配方法

概率密度匹配方法是通过调整模式结果，使其与实况观测的概率密度分布一致，从而实现订正。如概率密度匹配方法示意图所示(图5)，当实况出现8 m/s以下风速时，模式的概率密度要高于实况观测，当实况出现8 m/s 以上风速时，模式的概率密度要低于实况观测。如图5 中红色箭头所示，将模式的概率密度向实况观测进行调整，即可实现对风速预报的客观订正。具体步骤如下：(1)利用公式(1)计算实况观测风速出现不同风速阈值时的频率，建立实况风速值与实况风速频率的函数f(x)；(2) 利用公式(1)计算数值模式预报的10 m风速出现不同风速阈值时的频率，并带入f(x)中，可求新的风速值；(3) 将步骤2 中所求解的风速值除以其对应的风速阈值，即可求解出不同风速阈值的订正系数。

图5 概率密度匹配方法示意图

图6为实况观测风速出现某一阈值的频率，随风速增大，实况观测出现频率明显降低。8 m/s 以上风速出现的频率为16.02%，20 m/s 以上风速出现的频率为0.748%，28 m/s 以上的风速出现的频率仅为0.096%。

图6 2017—2018年风速实况观测频率

由于大量级风速样本量较少，直接利用多项式插值方法建立实况风速值与实况风速频率的函数并不能实现对大量级风速的有效订正(图7a)。如图7a 所示，16 m/s 以上风速值所对应的风速频率均在0附近，将数值模式对于大量级风速预报的频率值带入到该函数中并不能合理地求解出其所对应的风速值，难以实现对大量级风速的有效订正。为突出大量级风速的重要性，在构建函数前对实况风速频率进行ln函数处理(自然对数)，建立实况风速值与实况风速频率自然对数的函数，数学表达式如公式(2)所示：

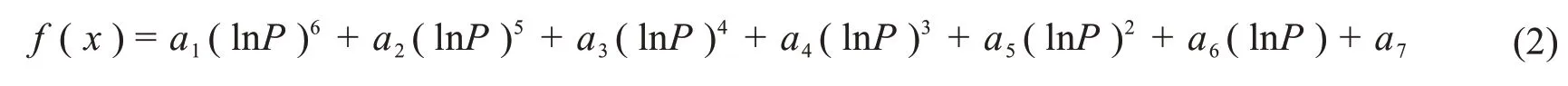
式中，f(x)为实况风速，lnP为实况风速频率对数，a1～a7分别为-0.000 6、-0.018 8、-0.213 1、-1.141 7、-3.185 1、7.341 1、0.412 1。利用多项式插值方法(6 次插值)建立的实况风速值与实况风速频率自然对数的函数如图7b所示。经自然对数处理后的风速频率越小，其对应的负值越大。16～28 m/s 的风速值对应着-5～-9 的值。将模式对于大量级风速预报的频率自然对数值带入到该函数中，可合理地求解出其所对应的风速值，进而实现对大量级风速的有效订正。

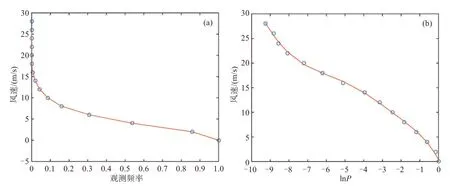
图7 风速实况观测与风速实况观测频率(a)、风速实况观测频率自然对数(b)的函数

图8 为根据上述方法求解出数值模式在24 h预报时效中不同风速阈值的订正系数，订正系数随风速的增加而增大，从2 m/s 的0.53 增加到28 m/s 的1.34。对于2～6 m/s 的风速，由于模式预报频率高于实况出现的频率且有明显的正平均误差，其订正系数均在1 以下；对于8 m/s 风速，模式预报频率与实况出现频率相当，其订正系数近似为1；对于10 m/s 以上风速，其订正系数均在1 以上；对于20 m/s以上的风速，订正系数在1.3附近。总体上，订正系数与模式预报误差特征较一致，小量级风速的订正系数小于1，大量级风速的订正系数大于1。

图8 ECMWF模式24小时10 m风速预报订正系数

5 检验分析

为进一步验证概率密度匹配方法对我国近海海域风速预报的订正效果，将上述方法所求解出的不同预报时效不同风速阈值下的订正系数带入到2019 年ECMWF 模式的10 m 风速预报中，并进行站点误差检验(图1 所示站点)及冷空气大风和台风大风天气过程的对比分析。

5.1 站点检验

图9 为2019 年1—12 月48 h 风速预报订正前后的平均误差对比。对于实况出现3 级及以下风速的预报，订正后风速的正偏差较订正前有所减小，表明对于3级及以下风速预报的偏大程度有所降低。对于实况出现5级及以上风速的预报，订正后预报的负偏差较订正前均有减少，尤其8、9级风速的负偏差减少程度明显，表明订正后对于大量级风速预报效果有所改进，且风速越大，改进程度越为明显，12～120 h 中其他预报时效的风速预报与48 h预报时效的的平均误差情况基本一致(图略)。

图9 2019年1—12月48 h风速预报订正前后平均偏差对比

平均误差的改善并不能足以证明订正后风速预报的改善，过量的空报同样可使大量级风速预报的平均误差降低。为验证概率密度匹配方法可有效提升对大量级风速的预报效果，计算了2019年1—12 月实况出现8、9 级风时订正前后的平均绝对误差(图10)。如图10 所示，当实况出现8、9级风速时，订正后风速的平均绝对误差在各个预报时效均小于订正前。在12 h 预报时效中，订正前8、9 级风速预报的平均绝对误差分别为4.15 m/s、5.61 m/s，订正后风速预报的平均绝对误差分别为3.12 m/s、4.08 m/s。在120 h 预报时效中，订正前8、9 级风速预报的平均绝对误差为7.38 m/s、9.35 m/s，订正后风速预报的平均绝对误差分别为6.46 m/s、8.07 m/s。

图10 2019年1—12月8级、9级10 m风速预报订正前后平均绝对误差对比

表1 为2019 年1—12 月ECMWF 模式10 m 风速预报订正前后漏报率对比，其中括弧外为订正后的漏报率，括弧内为订正前的漏报率。漏报率计算公式如下所示：

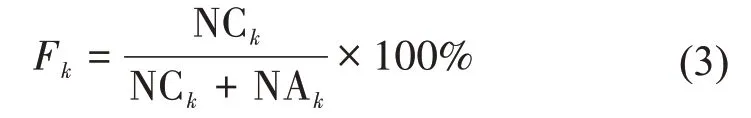
式中F为漏报率；NA 表示为预报正确，即预报大于某一量级风速且实况也大于该量级风速；NC表示为漏报，即实况大于某一个量级风速但预报未达到；k表示不同风速级别。在各个预报时效中，当实况出现4～5级风时，订正前后的漏报率基本相当，表明基于概率密度匹配方法的风速订正并未造成小量级风速的漏报。当实况出现6 级及以上风速时，订正后的漏报率要明显低于订正之前，尤其实况出现7 级以上风速时，大部分预报时效的漏报率可减少10%以上。

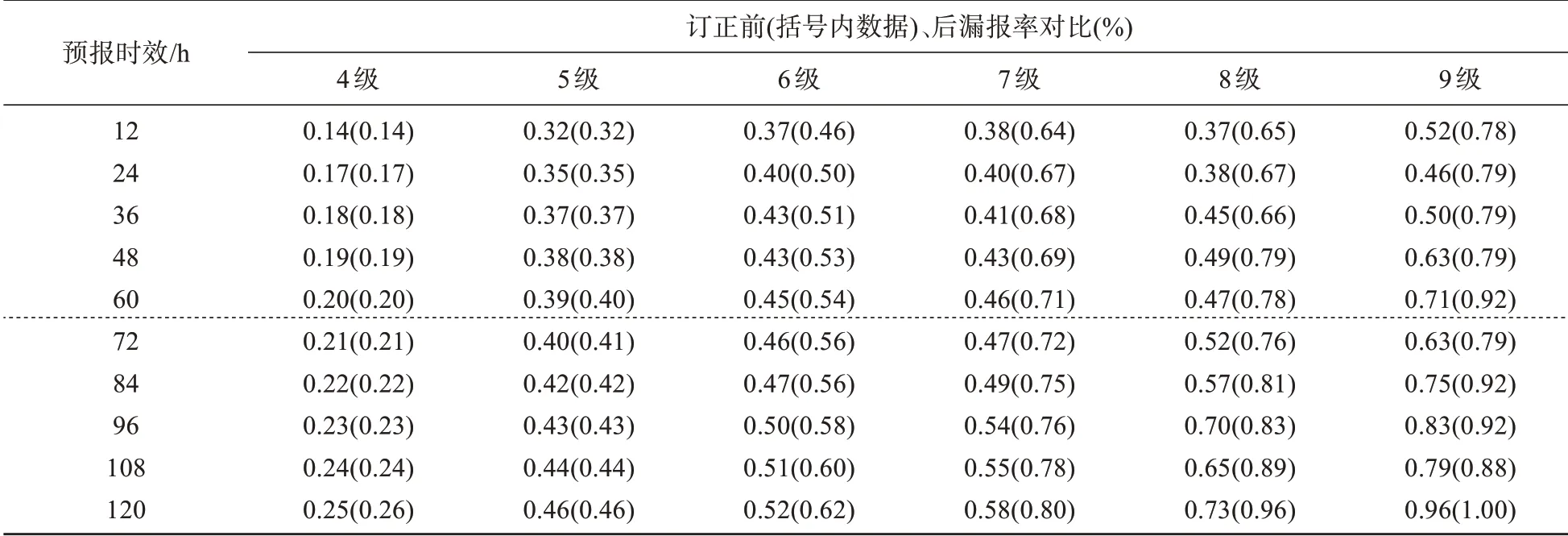
表1 2019年1—12月ECMWF模式10 m风速预报订正前后漏报率对比

通过站点的误差及空报率的检验表明，基于概率密度匹配方法的风速订正可有效改善数值模式对大量级风速预报偏小、小量级风速预报偏大的情况，且不会造成空报。

5.2 2019年1月15日渤海冷空气大风

2019 年1 月13—16 日，高空槽东移引导冷空气快速南下，造成我国出现一次明显冷空气过程。1 月15 日，地面冷高压中心位于我国河套地区，中心强度达1 040 hPa 以上，渤海位于高压东侧的等压线密集区中，出现了较大范围7级的偏北风。图11 为2019 年1 月15 日08 时(北京时，下同)地面风速观测实况。

图12 分别为2019 年1 月12 日08 时订 正前及订正后的72 h 预报时效的10 m 风速预报。订正前ECMWF模式在渤海以6级风为主，仅在渤海中部海域预报出个别的7级风，预报较实况明显偏弱(图12a)。利用概率密度匹配方法订正后的预报在渤海预报出大范围7 级风，与实况观测更接近(图12b)。

图11 2019年1月15日08时风速观测实况(≥13.9 m/s)

图12 2019年1月12日08时ECMWF模式72 h预报时效10 m风场预报(a)及风速订正后10 m风预报(b)

5.3 1918号台风“米娜”大风

2019 年9 月29 日—10 月2 日，受1918 号台风“米娜”的影响，我国近海出现了一次明显的大风天气过程。如图12 所示，台风“米娜”于9 月29 日开始影响我国近海海域，在趋向我国近海期间强度不断增强，9 月30 日20 时，其强度达到最强为40 m/s。10 月1 日08 时后，台风“米娜”的强度开始减弱，20 时30 分前后登陆我国浙江舟山时的强度为30 m/s(强热带风暴级)[30]。“米娜”始终沿西太平洋副热带高压外围环流运行，在我国近海海域北上登陆后转向东北。数值模式对于“米娜”的路径预报相对准确，但强度预报明显偏弱，其可能是由于人们对台风结构和强度变化的复杂性以及海陆气相互作用缺乏足够的认识或模式分辨率较低造成的[31-32]。

2019 年10 月1 日08 时我国浙江南部沿海观测站中出现了10～11 级大风，个别站点风力达12级(图14)。2019 年9 月29 日08 时起报的ECMWF模式在48 h预报中仅对我国浙江南部近海海域预报出9～10 级风，个别格点风速达11 级，明显较实况观测偏小(图15a)。订正后的48 h 风速预报在我国浙江南部近海预报出10～11 级大风，个别格点风速达12 级(图15b)。总体上，订正后的风速预报与实况观测及中央气象台台风定强(38 m/s)更接近。在风速订正前后差异图中可看出(图15c)，概率密度匹配方法主要是针对台风外围大风速区进行订正，风速增幅大值区主要集中在台风中心的北侧，增幅最大达8 m/s 以上。对于受台风“米娜”的影响较小的东海北部海域，订正前后风速变化不大。

图13 台风“米娜”路径图

图14 2019年10月1日08时观测实况(≥24.5 m/s)

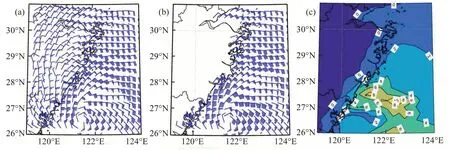
图15 2019年9月29日08时ECMWF模式48 h预报时效10 m风预报(a)、订正后48 h预报时效10 m风速预报(b)、订正前后风速差(c)

针对此次大风天气过程，比对了小明甫岛站2019 年9 月28 日08 时—10 月1 日08 时36 h 预 报时效订正前后的风速(图16)，小明甫岛站的位置如图12 中蓝色标记所示。在9 月28 日08 时—30日08 时1918 号台风“米娜”影响前，订正前后风速基本一致，并与实况较接近。随着台风“米娜”的不断北上，9 月30 日20 时，小明甫岛站的风力达14 m/s，订正前风速预报为12.1 m/s，订正后风速预报为13.8 m/s。10 月1 日08 时，小明甫岛站风力达29 m/s，订正后风速预报与实况较一致，订正前的风速预报较实况偏小近4.5 m/s。通过对小明甫岛站订正前后风速的对比可发现，基于概率匹配方法的风速订正对大风预报的改进效果明显，且对小风不会造成明显空报。

图16 小明甫岛站2019年9月28日08时—10月1日08时36 h预报时效订正前后风速对比

6 小结与讨论

本文利用中国气象局地面气象观测数据及12～120 h 预报时效的ECMWF 模式10 m 风预报数据，在统计数值模式10 m 风速误差的基础上，采用概率密度匹配方法对其进行订正，通过对独立样本的对比检验得出以下结论。

(1) 概率密度匹配方法可有效地改善数值模式10 m 风速预报对于小量级风速预报偏大、大量级风速预报偏小的误差特点，订正后各个预报时效、各个风速量级的预报平均误差均较订正前有所降低。

(2) 统计检验表明：采用概率密度匹配方法的订正，12 h预报时效的8、9级风速预报的平均绝对误差分别由4.15 m/s、5.61 m/s 降低至3.12 m/s、4.08 m/s。120 h 预报时效的8、9 级风速预报的平均绝对误差由7.38 m/s、9.35 m/s 减小至6.46 m/s、8.07 m/s。7级及以上风速的漏报率可减少10%以上。

(3) 个例检验表明：在渤海冷空气大风及台风大风天气过程中，订正后风速均较订正前有明显改进，与实况观测更接近。

基于概率密度匹配方法的我国近海洋面10 m风速订正效果依赖于代表站点的选取及数值模式预报能力。本文中所选取的代表站点基本覆盖我国东海东部沿岸和近海区域，求解出的风速订正系数可试用于我国近海。但不同月份的实况风速观测频率略有不同，后期可按照不同月份进行订正系数的求解，订正效果会更好。单一模式预报能力有限，对于某些可预报性较差的天气过程，订正方法仍需进一步检验分析。充分发挥不同预报中心数据模式的优势，将多模式集成与概率匹配方法进行有效结合，以期取得更好的预报效果。