降雨入渗对微生物注浆加固边坡的稳定性影响研究*
胡其志 , 刘彻德 , 丁志刚 , 包文成
(1.湖北工业大学土木建筑与环境学院,湖北 武汉 430068;2.中交路桥南方工程有限公司,北京 100027)
0 引言
在我国南方大部分地区,自然状态下或工程原因分布着众多土质边坡。工程措施可以加固土质边坡,其中利用微生物注浆加固边坡土体,以提高土质边坡稳定性具有较好的工程应用价值。同时,丰沛的雨水常导致边坡土体处在非饱和状态,持续的降雨使雨水渗入到边坡土中,导致边坡土体饱和度增加,非饱和土的基质吸力减小,引起边坡土体抗剪强度大幅降低,发生滑坡灾害的可能性大幅提升。因此对微生物注浆加固边坡进行降雨入渗条件下的稳定性研究具有很好的理论和工程应用价值。
目前,为解决非饱和土边坡在降雨入渗情况下稳定性问题,相关学者做了一些研究。石振明等[1]对堆积层边坡滑移机制进行了研究,认为降雨所引起的土体内部孔隙水压力升高是导致边坡失稳的重要原因;Cuomo等[2]对不同土-水特征曲线的土体进行渗流模拟,得到土-水特征曲线会对边坡内部的渗流过程产生明显影响。李东升等[3]根据植被根系含水固土稳定浅层边坡,美化生态环境的同时,保证工程建设破坏的生态环境能得到快速恢复,并随着植物的生长发育,对保持坡面稳定性和抗侵蚀能力有着积极显著作用。传统防护技术[4-6]可获得较好的加固效果,但同时也存在着施工成本较高、施工工艺比较复杂、后期维护保养费用较高,修复和更新难度大等问题。相较于传统的加固措施,微生物注浆技术[7-10]具有施工扰动小、修复和更新快等优点,在边坡防护方面有着较好的应用前景。微生物注浆技术通过胶结松散土体达到改善土体力学特性,是一种绿色的加固方法。
因此,依托室内试验和土-水特征曲线数据,借助数据分析软件 Origin,拟合出注浆前后土体的土-水特征曲线,得到边坡土体基质吸力随降雨入渗的规律。利用MIDAS/GTS有限元分析软件,对经微生物加固的边坡进行降雨条件下饱和-非饱和的非稳定渗流场模拟,研究降雨持时和注浆加固厚度对注浆边坡稳定性的影响。
1 微生物加固机理
微生物诱导生成碳酸盐沉淀(Microbial induced calcite precipitation,简称MICP)是自然界普遍存在的一种生物诱导矿化作用,即吸附在土体颗粒表面的微生物新陈代谢活动产生碳酸根离子与碱性环境中存在的金属离子发生胶结作用,原位诱导生成碳酸盐沉淀。当土颗粒表面形成的碳酸盐堆积但没有将其他土颗粒胶结在一起时,碳酸盐起到填充作用,可降低试样土的孔隙率。当土颗粒表面形成的碳酸盐堆积将土颗粒胶结形成一个整体时,碳酸盐起到胶结作用,可提高试样土的力学特性[11-13]。图1是以碳酸钙晶体为胶结物的MICP胶结过程的示意图。

图1 胶结过程示意图Fig.1 The process of calcium carbonate cementation
当一定浓度的菌液吸附到砂土颗粒之间的缝隙时(图1(a)所示),菌液与砂颗粒表面的碳酸钙晶体产生化学反应生成聚集的碳酸钙晶体,填充在砂颗粒周围(图1(b)所示)。进一步发生反应,聚集的碳酸钙晶体产生胶结作用,使得砂土颗粒之间产生了一定的粘聚力(图1(c)所示),从而提高了砂土的抗剪强度。利用微生物的MICP作用将边坡土体颗粒胶结填补贯通的孔隙,增加土体承载力的同时,减少土体贯通的孔隙,达到提升边坡稳定性的目的。
2 降雨入渗分析
在非饱和土力学理论中,土-水特征曲线在斜坡稳定性评价及降雨型滑坡预测等方面被广泛应用。土-水特征曲线反映着土的体积含水量或饱和度与基质吸力的关系,研究含水量对非饱和土力学性质的影响,实质上就是研究非饱和土力学性质与基质吸力以及土-水特性曲线的相互关系[14]。非饱和土中水的运动是瞬态渗流的动态过程。为了准确分析这一动态的过程,Fredlund和Margenster[15-16]提出体积含水率仅与孔隙水压的相关。结合Richards方程,推导出非饱和渗流的基本方程:

式中:Q为流量(m3);θ为体积含水量(%);φ为总水头(m),φ=z+h;z为位置势;h为孔隙水压力;kx、ky、kz为相应方向的渗透系数(m/s);t为时间(h)。
由上式可知,土的非饱和渗透特性主要包括持水性能和渗透性。为了定量描述土体的持水性能,已有大量学者拟合了一系列经验模型,其中Van Genuchten模型应用较为广泛,有效饱和度与孔隙水压力的关系式为:
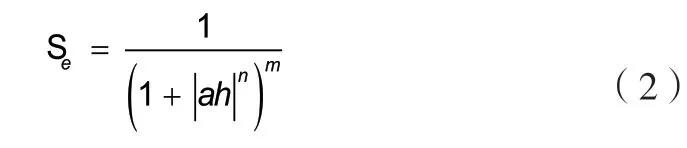
式中:se为有效饱和度;a为标定参数,它与土壤平均孔隙半径成正比;h为孔隙水压力;n和m分别为土-水特征曲线的形状参数和孔隙分布指数,且有n=(1-m)-1;θS为饱和含水率(%);θr为残余含水率(%)。结合有效饱和度的定义式:

联立(2)、(3)两式,在VG模型中建立的土-水特征曲线模型中,建立如下有效饱和度与孔隙水压力或基质势之间的关系式[18]:

Van Genuchten在1980年将其导出的土-水特征曲线模型与Mualem模型相结合,给出特定解析式的 VG-Mualem模型:

式中:ks为饱和渗透系数(cm/d);k(θ)为非饱和渗透系数(cm/d);其余参数含义同前。用孔隙水压力h表示非饱和渗透系数的表达式为:
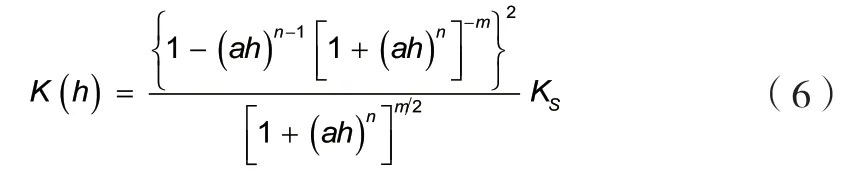
对于非饱和多孔介质来说,其渗透系数为饱和度和体积含水量的函数,由于体积含水量和饱和度与孔隙水压力之间的关系可以用土-水特征曲线来体现,因此渗透系数也是基质吸力的函数[17-19]。只需求得边坡土体中的土-水特征曲线相关系数,就可利用MIDAS/GTS有限元分析软件对边坡稳定性进行分析,从而得到降雨入渗过程中边坡稳定性变化过程。
3 数值模拟
选取某路堑均质边坡为研究对象,为了减少边界对模拟的影响,建立了一个长为40m、高为18m、倾角为41°的边坡几何模型,对坡面沿垂直坡面方向进行微生物注浆加固处理,设定的加固厚度分别为0.5m、1.0m和1.5m,如图2所示。该模型的上边界为地表的大气边界,两侧边界均为无流动边界,底部边界由恒定地下水位的压力水头边界组成,初始地下水位水平且初始水头高5m,施加的降雨强度分别为10mm/d、20mm/d和30mm/d,持续6h,每隔2h记录一次。为了提高计算时的精度,模型坡面的网格划分较为密集,使其在迭代计算过程中具有更好的敏感性。

图2 模型尺寸Fig.2 Model dimension
以MIDAS/GTS有限元数值分析软件为平台,分析不同降雨条件下,边坡表面及内部的渗流规律。边坡土体为砂质土,对土样进行力学指标试验及降雨入渗条件下的土体参数的采集。利用该土样在室内做了分批次连续微生物注浆加固试验。利用对土壤无公害反硝化细菌的反硝化作用进行MICP加固试验(注浆两周),完成注浆土的力学指标参数及降雨入渗条件下的土体参数的采集[20-21]。表1为在不同基质吸力条件下土体的体积含水量试验数据,借助数据分析软件Origin拟合确定土-水特征曲线中相关参数值。注浆前土样的土-水特征曲线参数值相关系数R2=0.997 4,注浆后土样的土-水特征曲线参数值相关系数R2=0.998 8,参数如表2所示。
4 结果分析
考虑降雨入渗对边坡稳定性的影响,计算初始水头地下水位的稳定渗流状态,得到雨水入渗的初始条件。根据计算得到的稳定流动状态孔隙水压力分布情况,对降雨强度30mm/d,降雨4h的孔隙水压力进行分析,各模拟方案中边坡孔隙水压力矢量云图见图3至图6。

表1 土体在不同基质吸力下的体积含水量Tab.1 VWC of soil samples under different matrix suction

表2 模拟中边坡模型的参数取值Tab.2 Slope soil parameter value

图3 注浆加固前降雨4h孔隙水压力云图Fig.3 Color vector picture of PWP of unreinforced initial slope after 4 hours of rainfall

图4 加固厚度0.5m降雨持时4h的孔隙水压力云图Fig.4 Color vector picture of PWP of Reinforce the slope of 0.5m thickness after 4 hours of rainfall

图5 加固厚度1.0m降雨4h孔隙水压力云图Fig.5 Color vector picture of PWP of Reinforce the slope of 1.0m thickness after 4 hours of rainfall
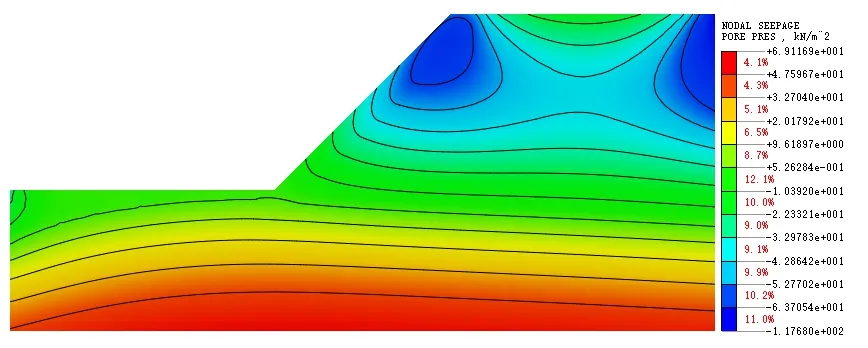
图6 加固厚度1.5m降雨4h孔隙水压力云图Fig.6 Color vector picture of PWP of Reinforce the slope of 1.5m thickness after 4 hours of rainfall
由土的持水性能可知,体积含水量的变化可以反映出土体的基质吸力的变化和体积含水量。由图5所示,在注浆加固前,地表渗透能力在降雨前期较强,雨水全部入渗,坡体内孔隙水压力为负值,降雨入渗导致孔隙水压力从负值向正值发展,孔隙水压力大幅增大,随着降雨时间增长,浸润线由水平状态发生变化,靠近坡脚处的浸润线受降雨影响逐渐升高,上升区域的土体达到饱和状态,土体的含水量自坡顶呈现出大-小-大分布,基质吸力随降雨的延续而逐渐减小。
由图6至图8所示,在注浆加固后,坡面区明显存在孔隙水压力负值区,这是由于注浆加固的坡面渗透性低,由坡面入渗的雨水较由坡顶入渗的少,且注浆土的持水性较未注浆土强,使雨水的持续下渗过程受阻,因而在坡面区形成了孔隙水压力负值区,但随着降雨的持续进行,这个负值区会向坡体内部移动,最终坡体的含水量依旧呈现出大-小-大分布。
此外,各模拟计算结果变化规律类似,随着降雨持时的增加,坡体内分离的孔隙水压力负值区将增大并移动连成一片,向边坡体内部移动,边坡内部逐渐形成危险滑移面并贯通,诱发边坡失稳。微生物注浆坡面对雨水进入坡体的过程有延时效果,且延缓效果与加固厚度正相关,边坡失稳的时间随着加固厚度的增加而增加。
对不同加固方案在不同降雨强度、不同降雨持时的计算可知,不同加固方案降雨强度与降雨持时对边坡稳定性的影响,见图7至图10。
由图7至图10可知:注浆加固前,在降雨强度为20mm/d、降雨持时为2h时发生破坏;加固厚度0.5m的加固方案在降雨强度为30mm/d、降雨4h和降雨强度为20mm/d、降雨6h发生破坏;加固厚度1m的加固方案在降雨强度为30mm/d、降雨6h发生破坏。随着降雨强度的增加,边坡的稳定性系数在降低;在降雨持时相同,随着降雨强度的增加,各方案的稳定系数的降低幅度随加固厚度的增加而减小。在降雨强度相同,随着降雨持时的增加,各方案的安全系数在迅速降低。在降雨持时为6h,加固厚度为1.5m的边坡的在30mm/d的降雨强度下,安全系数只有1.2。不难推测,随着降雨的继续进行,加固厚度为1.5m也将破坏。安全性系数偏低与采用的计算参数以及微生物注浆周期短有很大关系,但通过已有的模拟结果可以得出,经微生物加固坡面的边坡在降雨入渗条件下的稳定性变化是正向的。
5 结论

图7 注浆加固前降雨持时与边坡稳定性关系Fig.7 Relationship between rainfall duration and slope stability before grouting reinforcement

图8 加固0.5m降雨持时与边坡稳定性关系Fig.8 Relationship between rainfall duration and slope stability of 0.5m thickness

图9 加固1.0m降雨持时与边坡稳定性关系Fig.9 Relationship between rainfall duration and slope stability of 1.0m thickness

图10 加固1.5m降雨持时与边坡稳定性关系Fig.10 Relationship between rainfall duration and slope stability of 1.5m thickness
采用MIDAS/GTS软件探讨了降雨入渗过程对微生物注浆加固的非饱和土质边坡稳定性影响,对三种不同加固方案进行了数值模拟与分析,得出以下结论:
1)在降雨入渗情况下,利用拟合的土-水特征曲线,得出非饱和渗透性函数的特征参数,借助 MIDAS/GTS软件对经微生物注浆加固的边坡进行了数值模拟。模拟结果表明,在相同降雨条件下,边坡变形至失稳的过程中,微生物注浆加固可以有效减小降雨入渗对边坡的影响,对提高边坡的稳定性具有明显的促进作用;相同加固方案、相同降雨持时情况下,降雨强度越大,边坡的稳定性越差,其中当降雨强度达到30mm/d时,所有加固方案的边坡处在失稳状态。
2)由土-水特征曲线可知,随着土体中的水分在不断增加,易诱发滑坡等地质灾害。当坡面经微生物注浆加固后,降低了坡面的渗透能力,延缓了雨水进入坡体的过程。模拟结果表明,在降雨持时相同时,经加固后的边坡随着加固厚度的增加,孔隙水压力负值区在不断减少,有利于边坡稳定。
3)对三种加固厚度的方案,在不同降雨强度条件下的边坡稳定性进行了研究。参考的试验数据和加固方案都有一定的局限性,对于更复杂的边坡形式及降雨条件以及加固方案的选择等因素下的微生物注浆边坡仍需进行进一步研究。通过已有的模拟结果可以得出,经微生物加固坡面的边坡在降雨入渗条件下的稳定性变化是正向的,微生物注浆技术是提高边坡稳定性的有效途径。

