GAMIT/GLOBK数据解算误差影响分析*

苏晓庆，王 晖，徐 工

(山东理工大学 建筑工程学院，山东 淄博 255000 )

在处理高精度数据时，通常使用无电离层组合消除一阶电离层延迟，但残余的高阶电离层项延迟也会对定位结果产生厘米级的影响。对流层延迟在天顶方向的误差约为2.3 m，低高度角的误差最大可达20 m，是高精度数据处理不可忽略的影响因素[1]。在沿海地区，海潮负荷引起的形变可达数厘米，因此在GPS高精度数据处理中必须考虑海潮负荷的影响[2-3]。目前，已有大量的研究人员分别对上述误差改正进行了详细的研究，但在实际工程应用中缺少对各种误差改正的综合分析。因此，本文采用GAMIT/GLOBK对GPS控制网静态数据进行解算，综合考虑高阶电离层影响和基线解算模式、映射函数模型和对流层参数、概略坐标误差、海潮负荷和固体潮模型对解算结果的影响，结合本次实验项目，分析和设计静态数据解算策略，提高数据处理精度。

1 GPS数据解算影响因素

1.1 电离层延迟

电离层延迟是GPS数据采集与处理过程中的重要误差源，如何削弱电离层延迟的影响是提高定位精度的关键因素。载波相位一阶、二阶和三阶的电离层延迟量可以表示为：

(1)

式中，δ1、δ2、δ3分别为一阶、二阶和三阶电离层延迟量；Ne为自由电子密度；B为站星连线与电离层薄层交叉点处的地磁场强度；θ为卫星信号矢量与地磁场强度矢量在电离层交叉点处的夹角[4]。

1.2 对流层延迟

GPS测量中常用的对流层延迟改正模型有霍普菲尔德(Hopfield)模型、萨斯塔莫宁(Saastamoinen)模型等，GAMIT对流层延迟改正的缺省模型是SAAS模型[5-6]，即：

(2)

E′=E+ΔE

(3)

(4)

a=1.16-0.15×10-3h+0.716×10-3h2

(5)

式中，h为测站高程；Ps和es为测站上的气象元素，分别为气压和水汽压；E为卫星高度角；ΔS为对流层折射改正。

信号传播路径上的对流层延迟STD与测站天顶方向的对流层延迟ZTD(Zenith Tropospheric Delay)间有如下关系：

STD=m×ZTD

(6)

式中，m称为投影函数，是卫星高度角E以及其他因素的函数，其好坏将直接影响对流层延迟改正的效果。

1.3 测站概略坐标误差

概略位置坐标由接收机提供，其精度能够影响周跳探测能力的好坏，概略坐标误差越大，周跳探测能力越弱[7]，即基准站坐标的精度将影响基线解算的精度，最大影响可以表示为：

ΔL=0.60×10-4×L×Δε

(7)

式中，ΔL为测站概略位置坐标对基线的影响；L为基线长度；Δε为测站坐标的误差。

1.4 海潮、固体潮负荷

海潮负荷对基线分量和测站坐标都有一定的影响，在GPS数据处理中顾及海潮负荷的影响，可以提高解算结果的精度。海潮负荷改正用下式表示[8]：

(8)

式中，LΔU、LΔE和LΔN分别为t时刻海潮负荷所引起的测站径向、东西方向和南北方向位移变化；ρ为海水密度；φ、λ为测站的纬度和经度；φ′、λ′为球坐标系下海洋潮汐负荷点的纬度和经度；Hi(φ′,λ′,t′)为点(φ′,λ′)处第i个分潮的瞬时潮高；A为测站到积分面元的方位角；Gl(Ψ)和Gr(Ψ)分别为横向和径向质量负荷格林函数，其中Ψ为球面角。

GAMIT在进行数据处理，应用固体潮改正模型时，由于三阶潮汐影响比较小，故只考虑二阶引潮位的影响[9-12]。二阶潮汐对测站位移的影响：

(9)

2 案例分析

为提高静态数据的解算精度，更好地分析误差对解算结果的影响，针对某矿区地表形变监测控制网进行高精度解算，专门采用中国周围精度较高的9个IGS站(AIRA、BJNM、CHAN、SHAO、TNML、WUH2、URUM、ULAB、YSSK)作为基准站，该控制网共有6个点(分别命名为JZ01、JZ02、JZ03、Q025、Q040、Q041)。

2.1 基线解算模式影响分析

要获得高精度测站定位结果，需要顾及高阶电离层的影响[13]。本文考虑了电离层二、三阶改正，其中VETC值来自IONEX文件，采用IGRF13地磁场模型。GAMIT提供多种基线解算类型：(1)适合长基线的LC_AUTCLN解(基于伪距求解宽巷模糊度的LC解)；(2)适合长基线的LC_HELP解(基于电离层约束求解宽巷模糊度的LC解)；(3)适合短基线的L1_ONLY解(双频观测中的L1解)；(4)适合短基线的L1L2_INDENT解(双频观测中独立的L1、L2组合差分解)等[14]。

各测站相隔距离为8～20 km，均属于短基线(短基线<100 km)。如果利用LC_AUTCLN或LC_HELP基线解算模式，将IGS站作为基准站去解算测站，会涉及长短基线混合解算的情况。GAMIT每次解算只采用一种基线解算模式时，LC_AUTCLN对各种误差进行模型改正，适合长基线解算。测站间隔短，环境相关性强，则采用差分L1L2_INDENT解算模式较合适。为了分析长短基线并存对解算结果的影响，设计了两种解算方案进行测站坐标解算，不同方案的解算坐标差值如表1所示。

方案一：采用LC_AUTCLN解算方法，利用9个IGS站共同解算6个控制网测站的坐标。

方案二：采用LC_AUTCLN解算方法，利用9个IGS站逐个解算6个控制网测站的坐标。

方案二分成6个GPS基线网，逐个解算6个测站坐标，此时各GPS基线网中不存在短基线，工作效率降低，但解算精度明显提高，从表1可以看出，基线解算模式会对解算结果产生毫米级的影响，并且对平面方向的影响要大于高程方向。本次实验项目中，平面精度最优提高6.52 mm，高程精度最优提高3.98 mm，因此，在实际项目中对精度要求高时，可以采用方案二模式。

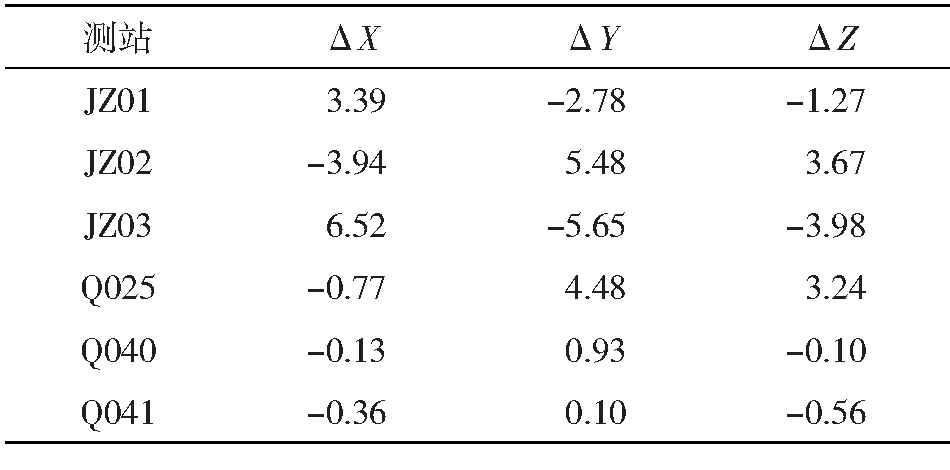
表1 两种方案测站坐标解算差值/mm

2.2 对流层延迟影响分析

GAMIT在对流层改正方面有很大的优势，其利用SAAS改正模型所求的对流层延迟改正值仅视为一种初始近似值，在数据处理过程中，仍把对流层延迟当做未知参数，通过平差计算去估计其准确值。GAMIT采用分段线性法，该方法将整个时段分为若干个区间，每个区间各引入一个参数。如果一天内测站天顶方向天气变化很大，则需要引入较多的参数，而引入的未知参数较多，易导致法方程秩亏，即矩阵不满秩的情况。本文以YSSK、CHAN基站为例对对流层参数个数的选取进行讨论，解算IGS基准站得到的坐标差值如图1所示。其中，坐标差值为解算得到的IGS坐标与ITRF2014提供的IGS坐标较差。

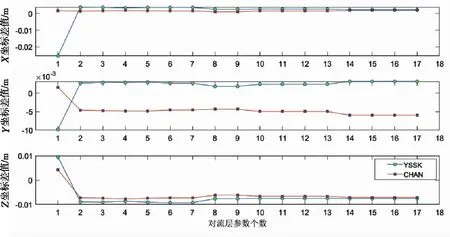
图1 不同对流层参数个数解算基准站坐标差

从图1可以看出，随着对流层参数个数的增多，解算坐标差值缓慢减小，当参数个数超过10个以后，测站坐标差值变化平稳。因此，在该实验项目中，在测站坐标单日解算中，对流层参数设置为8～10个时差值最小，解算结果最佳。

GAMIT 目前支持 GMF(Global Mapping Function)、NMF (Neill Mapping Function)和 VMF1(Vienna Mapping Functions 1)三种映射函数，但只有 VMF1需要引入模型文件。本文讨论了三种映射函数对基准站坐标解算的效果，结果如表2所示。

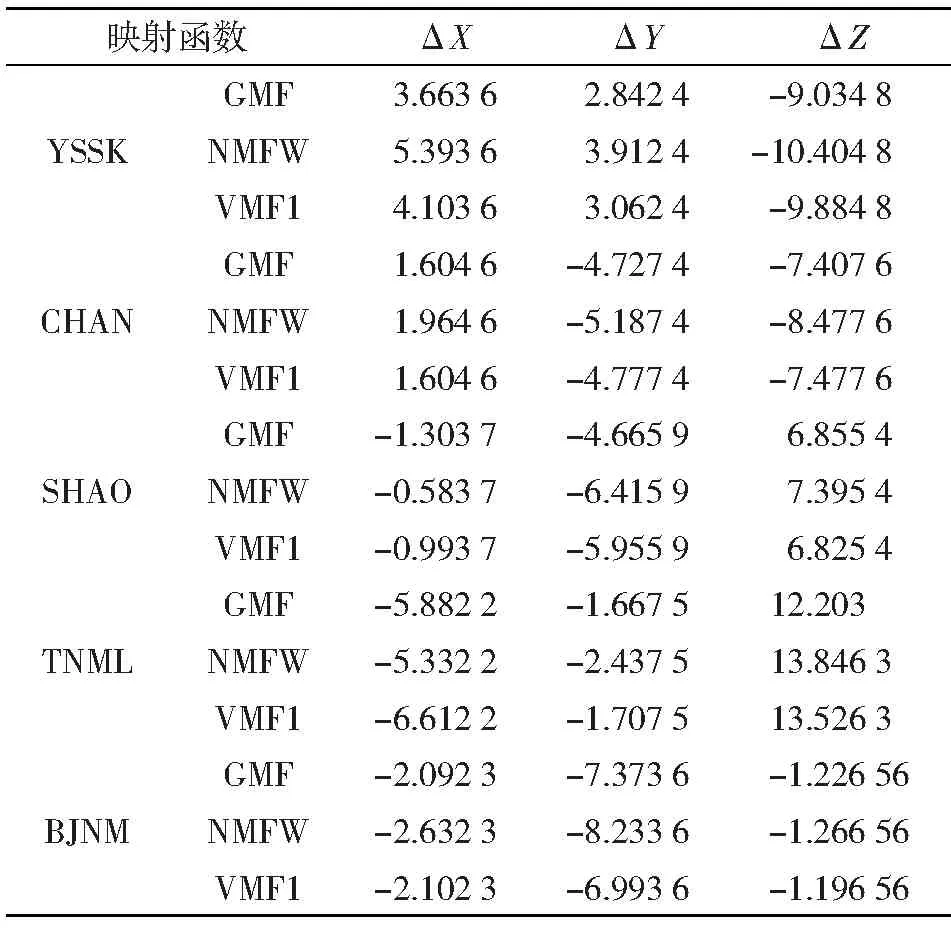
表2 不同映射函数基准站解算得到的坐标差值/mm

从表2可以看出，采用GMF映射函数解算精度最高，VMF1映射函数精度次之，NMFW映射函数精度最低。因此，在相似情况下，高精度定位中建议使用GMF映射函数。

2.3 概略坐标误差影响分析

在利用GPS进行定位时，高程方向受对流层、电离层等误差因素的影响远远大于水平方向，且地表监测网对高程坐标精度有很高的要求。本文针对基准站和控制网测站高程概略坐标误差对解算结果的影响，采用以下两种方案进行分析。

方案一：对9个IGS基准站高程坐标分别加入15 m、10 m、8 m、7 m、6 m、1 m、0.5 m、0.1 m误差。方案二：对6个测站高程坐标分别加入15 m、10 m、8 m、7 m、6 m、1 m、0.5 m、0.1 m误差。高程方向概略坐标加入误差与不加误差解算得到的坐标差值，结果如表3所示。

表3 测站高程方向解算坐标差/m

从表3可以看出，当基准站的概略坐标高程误差大于7 m时，会对解算结果造成很大的影响，当基准站概略坐标误差小于6 m时，GLOBK对基准站实行紧约束固定参考框架，对解算结果的影响很小。本文在解算过程中对基准站实行紧约束，所以控制网测站高程方向的概略坐标误差不会对解算结果产生影响。

2.4 海潮、固体潮负荷影响分析

GAMIT提供了4种海潮模型，otl_CSR4.grid、otl_FES2004.grid、otl_GOT00.grid和otl_NAO99b.grid模型，文献[15]针对GAMIT提供的4种海潮模型对基线的影响进行分析，得出NAO99b海潮模型适合山东地区高精度测量，该海潮模型是由日本天文台提出的，因此在日本和黄海等周围海域也有很高的精度。

本文讨论加载与不加载海潮模型改正对测站坐标的影响，解算结果如表4所示，可以看出，Z坐标的影响大于X、Y坐标，Z坐标差值最大为1.87 mm，在GAMIT/GLOBK中加载和不加载海潮模型改正对测站坐标解算影响不大，都可以满足一般工程要求。

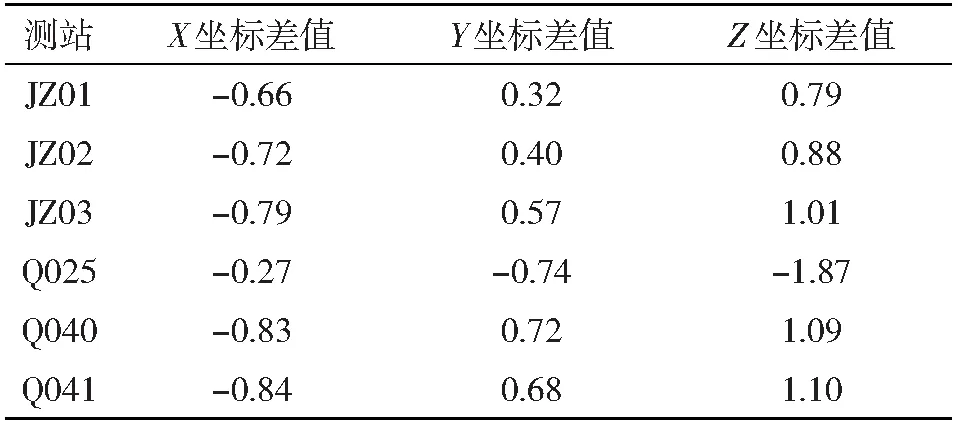
表4 控制网测站加载与不加载海潮模型解算得到的坐标差值/mm

下面选取JZ02站相关基线进行分析，从表5可以看出，随着基线长度的增加，海潮模型对基线差值的影响越大。基站分布对解算结果也有影响，总体来说，海潮模型对基站在沿海的影响要大于在内陆的影响。

表5 海潮模型对JZO2控制网测站基线的影响

需要特别注意的是，短基线解算时，固体潮对两个测站间的影响相近，在差分解算时可抵消。对于长基线解算，测站间隔较远，所受到固体潮的影响是不一样的，所以利用GAMIT进行长基线解算时，不可忽略固体潮的影响。GAMIT在解算时进行潮汐、非潮汐大气负荷改正，使用麻省理工学院提供的大气负荷位移全球格网数据，在数据解算过程中，根据大气负荷格网数据，我们内插出了测站处的大气负荷位移，并对观测值进行改正。

GAMIT/GLOBK提供使用IERS96、IERS03、IERS10三种固体潮模型，本文在GAMIT/GLOBK中使用不同固体潮模型对解算结果的影响进行分析。

如表6所示，在使用IERS10和IERS03模型进行解算时，测站Y坐标差值最大为2.52 mm，使用IERS96与IERS10模型解算得到的Y坐标差值达到3 mm，总体来看，差值较小，解算时采用IERS10模型即可。

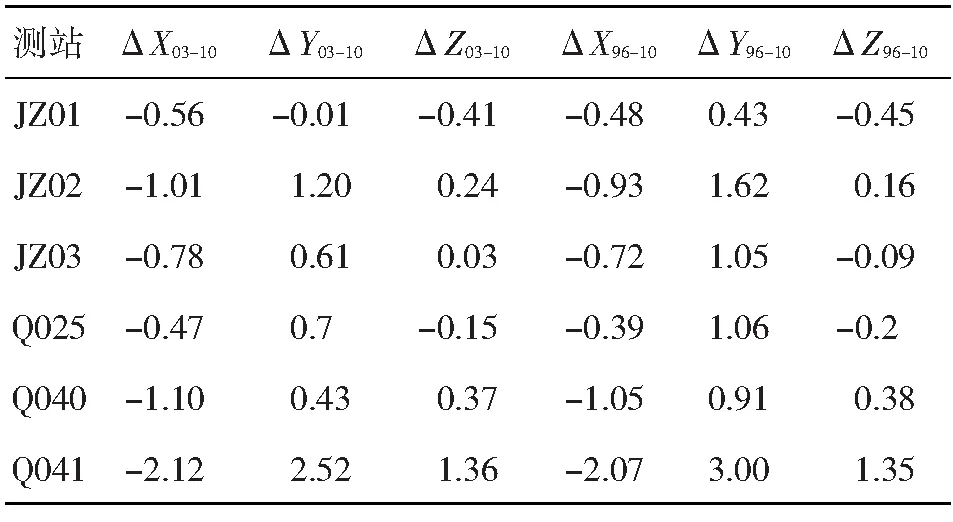
表6 不同固体潮模型测站坐标解算差异/mm

3 结 论

通过实验结果对比分析，基线解算模式、对流参数和概略坐标对解算结果的影响较大。数据解算时最好按照同种基线类型共同解算，不同类型分步解算。对流层参数个数也会对解算结果产生影响，随着参数个数的增加，解算精度随之降低。较大的基准站概略坐标误差会对解算结果产生很大的影响，数据解算时需将概略坐标误差控制在7 m以内。海潮模型对解算结果影响较小，此外，各种映射函数和固体潮模型解算得到的坐标值相差较小，采用GMF映射函数模型和采用最新IERS10规范中的固体潮模型即可。需要特别注意的是，分步解算的工作效率会有所降低，对于本文所提出的长短基线混合情况，解算模式的选择和计算效率的提高还需进一步研究。