地铁运行状态变化下杂散电流对埋地管道干扰数值模拟

董亮，陈金泽，姚知林，石超杰

地铁运行状态变化下杂散电流对埋地管道干扰数值模拟

董亮，陈金泽，姚知林，石超杰

（常州大学 石油工程学院，江苏 常州 213164）

研究地铁系统运行状态多变性导致地铁杂散电流对埋地管道的干扰规律。构建具有多个牵引区间、排流网、地铁站接地系统及停车场的地铁系统，埋地管道及其阴极保护系统等模型，基于数值模拟方法，采用专业软件计算地铁机车数量、位置及牵引电流变化，地铁排流网、站内接地系统和停车场与线路轨道电导通状况等地铁运行状态变化下轨道对地电位分布，轨道和排流网泄漏杂散电流密度分布，接地系统和停车场杂散电流量、以及杂散电流干扰时的埋地管道电位分布，分析确定地铁运行状态变化下杂散电流对埋地管道干扰规律。地铁系统采用焊接而成的长走行轨回流时，任何牵引供电区间内运行的机车及电流变化，均会对靠近地铁线路的埋地管道造成干扰，干扰有叠加效应。干扰最大位置出现在埋地管道与轨道的交叉点或并行段，且并行间距越小，最大干扰水平越接近交叉点处的干扰水平。当地铁排流网、站接地系统和停车场轨道不与线路轨道电连接时，能够一定程度降低干扰水平，当与轨道在局部电连接时，会使得邻近埋地管道所受干扰程度剧增。地铁运行状态变化致使埋地管道电位波动，且波动程度与机车运行状态、接地系统或停车场轨道频繁与线路轨道电连接状态、排流网性能及工作状态等地铁运行状态息息相关，在干扰检测和防护中应关注地铁运行状况变化。

地铁系统；杂散电流；干扰规律；数值模拟；埋地管道；运行状态

地铁轨道交通具有运载量大、安全快捷、受气候等因素影响小等优点，是中大型城市主要的交通方式之一[1]。城市地铁一般采用直流电力牵引的供电方式，采用接触网或第三轨为正极，全线连通的走行轨（即钢轨）兼作回流线回流至负极。钢轨铺设于道床之上，通过绝缘垫层与大地电气隔离，但受油渍污染、渗水潮湿、轮轨磨损散落的铁粉等因素影响，钢轨的轨地绝缘性能降低，会向周围土壤[2-3]和混凝土[4-5]等介质泄漏一定的电流，称为地铁杂散电流或迷流[2-3]。部分杂散电流在邻近埋地金属管道等具有良好导电性的结构上流入和流出，最终会回流至钢轨。杂散电流在埋地金属管道上的流入流出造成其保护电位发生波动[6-7]，在杂散电流流出点发生金属的阳极溶解反应，从而构成严重的电解腐蚀[8]，国内[9-13]和国外[14-16]均有多例报道。

埋地管道受地铁杂散电流干扰程度的影响因素众多，包括管道侧的因素（如管道规格、长度、埋深、数量、管道防腐层状况和阴极保护状况等）、地铁侧的因素（如牵引电流、轨道的纵向和过渡电阻等）以及二者之前的相对位置和土壤环境等因素。埋地管道上测得的管地电位波动特征则主要与地铁运行状态有关，是由于地铁牵引机车的运行数量和位置等时刻发生变化，泄漏杂散电流量及分布发生变化，因而产生的是动态的杂散电流，邻近管道某点处杂散电流的流入流出特性是变化的。这种变化与机车的运行状况（如运行位置和数量）、机车牵引电流变化、排流网和地铁站接地系统的工作状态及环境因素等息息相关，使得问题异常复杂[17-21]，给杂散电流影响规律的分析判断和缓解措施的设计提出了更高的要求。由于针对地铁杂散电流的现场研究相对复杂，变动参数不易，实施难度较大，而电路模型和数值模拟技术的发展为此研究提供了便利。目前关于地铁杂散电流分布规律的电路模型计算和数值模拟研究较多[21-23]，重点关注了牵引电流、牵引间距、轨道纵向电阻和过渡电阻、杂散电流排流网等设计因素或参数对杂散电流分布的影响。计算或模拟中通常过于简化问题模型，只考虑单个牵引区间、单列车的情况，且不考虑或简化考虑埋地管道和排流网等，由此得到的规律对设计有一定的指导意义，但难以指导发现或解决实际问题。

为弄清地铁杂散电流的分布规律及其对邻近埋地管道管地电位的影响，文中构建了包括多个牵引区间、多个车站和1个停车场，并考虑在线路沿线铺设排流网和在各站铺设接地系统的地铁系统模型，并加入埋地管道及其阴极保护系统。采用数值模拟技术研究机车运行状况、排流网和接地网工作状况以及埋地管道和地铁的相对位置关系对杂散电流干扰的影响规律，以期为地铁和埋地管道的选址设计、杂散电流干扰的检测及干扰防护重点提供技术指导。

1 地铁杂散电流干扰数值模拟方法

1.1 地铁杂散电流干扰模型

模型中设置的地铁线路、车站及与埋地管道的位置关系如图1所示。地铁沿线由7个牵引变电所双边供电，即有6个牵引区间组成，其中4个为正线区间，范围为0~14.4 km；1个为出入段线区间，范围为14.4~15.6 km；1个为停车场区间，范围为15.6~ 16.8 km。正线的每个牵引区间内还有2个车站，模型中设定所有站的间距相同，均为1.2 km。埋地管道与轨道间设置3种位置关系，即交叉、并行、交叉且并行。交叉关系包括90°交叉（位置1）和45°交叉（位置2）2种，交叉点位于(7.2, 0) km处；并行关系位置在地铁线路的5.2~9.2 km之间，并行间距为0、200、500 m（位置3、4和5），两侧管线45°远离；交叉且并行关系在位置6处，将后半段管道与轨道45°交叉，交叉点位于(9.4, 0) km处。

图1 地铁线路、车站及与埋地管道位置关系

将图1中虚线部分细化，得到地铁牵引电流、杂散电流排流网及接地系统，如图2所示[20]。轨道下方设有杂散电流排流网，每个站内各设单独的接地系统，接地系统间通过电缆相连或未连接，二者通过钢轨电位限制装置在站内的排流柜内连接到每个站的轨道上。停车场内轨道与线路轨道通过单向导通装置连接。严格意义上，地铁沿线各处均存在差异，杂散电流理论计算难以实现。为简化模型且同时避免给影响规律研究带来明显误差，通常可作以下假设[20-23]：走行轨、排流网和接地系统的纵向电阻、轨道和排流网对地的过渡电阻以及土壤电阻率是均匀分布的；各站接地系统的接地电阻是相同的；馈电线路的阻抗忽略不计。

图2 地铁牵引电流、排流及接地系统

1.2 数值模拟方法

1.2.1 埋地管道阴极保护系统

在均匀介质中，当阴极保护系统处于稳态时，介质中的电位分布满足如式（1）所示的Laplace方程[20-21,24-25]。该方程可通过有限差分法、有限元法或边界元法等数值计算方法求解，即通过构建系统几何模型、进行网格划分、设置边界条件和计算求解等4个步骤完成。其中，边界元法的几何模型、离散和计算都只在结构物/介质边界上，减少了未知数的个数，数据输入容易。阴极保护所需的即是结构物/介质边界上的电位和电流密度分布，因而该方法在阴极保护数值模拟中应用最广[20-21,25]。

在外加电流阴极保护系统中，所研究的区域由辅助阳极和被保护金属结构物的外表面、地表等绝缘表面组成。对于被保护金属结构物，其边界条件为电流密度和极化电位的非线性函数，即极化曲线，可通过实验测得。对于辅助阳极，由于其表面活性较高，可采用恒电流密度作为边界条件，即恒定的电流密度等于阳极输出电流除以阳极表面积。特殊地，绝缘表面如大地表面，基本无电流的流入流出，采用恒电流密度为0作为边界条件[20-21]。

1.2.2 地铁杂散电流

由于地铁列车为动态运行，模拟中考虑列车由多个连续的静态构成动态。此时地铁杂散电流的存在并不改变介质中电位分布所满足的方程，而是增加了铁轨、排流网和接地系统的边界条件及各个无电连接系统的电流自平衡条件。

以轨道为例，轨道纵向电阻和轨地过渡电阻g是确定钢轨直流电特性的2个参数。在数值计算中，可将工字型的钢轨等效成管状的金属结构，即采用管单元[20-21]，保持相同的纵向电阻和过渡电阻。在数值模拟中，纵向电阻可以直接设置，而过渡电阻则需要采用给定涂层电阻的方式处理，涂层电阻与过渡电阻（减去管状结构接地电阻后）的转换关系为：

式中：为等效的管状金属结构的外径。

此时轨道对地界面的边界条件可表示为：

式中：r和r分别为钢轨的泄漏电流密度和钢轨的对地电位；0为钢轨某点处与管道电位之差，由地铁系统电流自平衡条件（见式（4））结合电位控制方程及边界条件迭代求解得到：

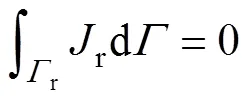
式中：r为钢轨的对地边界。该条件表明，地铁泄漏电流最终全部会回流至钢轨中。

对于排流网和接地系统，采用与轨道相同的方法即用涂层电阻来等效过渡电阻。当排流网和接地系统在不与轨道电连接时，也存在如式（4）所示的电流自平衡条件；当排流网或接地系统与钢轨电连接时，其对地边界与钢轨的对地边界共同组成统一的电流自平衡条件。该方法的可行性已得到验证[21]，文中结合该方法设置合理的参数，采用BEASY CP软件[20-21,25]开展数值模拟。

2 影响因素及模拟参数设置

2.1 地铁系统

在文中的数值模拟中，地铁系统的基本参数见表1。其中，模型中与钢轨、排流网等效的管状金属结构直径为0.05 m，该几何结构接地电阻为0.09 Ω·km，则过渡电阻3、1、0.1 Ω·km等效的涂层电阻分别为456.9、142.9、1.57 Ω·m2。

2.2 埋地管道及阴极保护系统

选取的埋地管道规格为508 mm×8.0 mm，长为40 km，埋深为2 m。管材电阻率取0.135 Ω·mm2/m，计算得到纵向电阻为1.074×10‒5Ω/m。埋地管道由涂层和外加电流阴极保护系统联合保护，在室内通过动电位扫描法测试获取裸露管材在土壤中的极化曲线，扫描速率为0.5 mV/s。计算时选取其中50组数据[25]，参照BS/ISO 15589-1—2015[26]，将电位保持不变，对应的电流密度乘以涂层破损率得到涂层管在土壤中的边界条件（如图3所示）。由此计算得到的管道电位为管道对地通电电位，是相对于铜/饱和硫酸铜参比电极（简称CSE，以下电位均相对于该参比电极）的电位，涂层管的最小阴极保护电流密度为0.01 mA/m2。埋地管道由一套埋深为80~100 m的深井阳极提供外加电流保护，深井阳极距管道水平距离为300 m，输出电流为2 A。

表1 模拟中地铁系统的基本参数

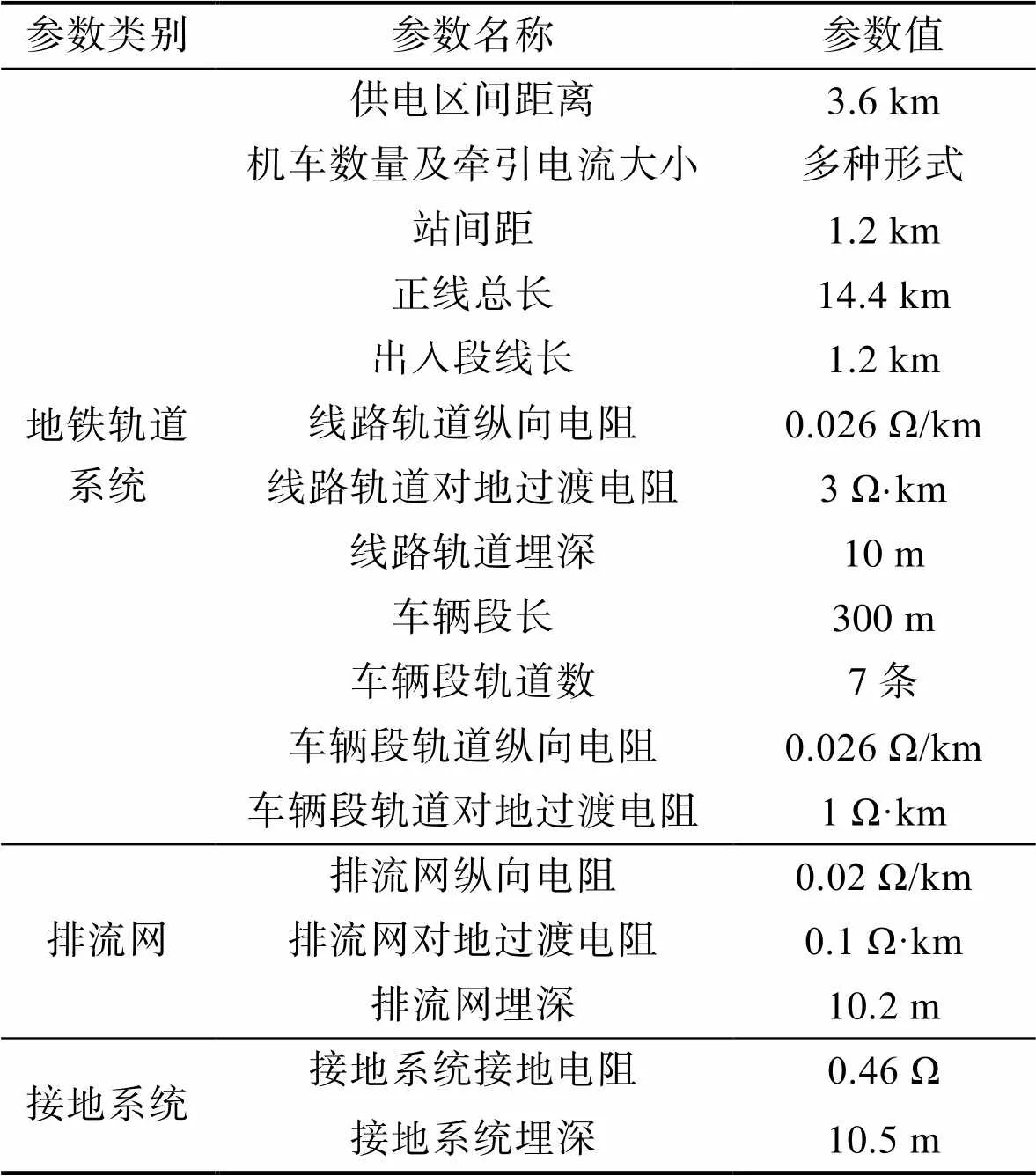
Tab.1 Basic parameters of metro system in numerical simulation

图3 涂层管在土壤中的极化边界条件

2.3 土壤环境

文中设置的土壤为单层土壤。由于我国有地铁的城市主要分布在华中、华东、东北和南方等区域，这些区域土壤电阻率大多低于100 Ω·m[27]。计算时，土壤电阻率选取中间值，为50 Ω·m。

3 结果与讨论

3.1 地铁系统未运行时的埋地管道电位分布

当地铁系统未运行（即无地铁杂散电流）时，有外加电流阴极保护的埋地管道的保护电位分布如图4所示。埋地管道保护电位处于‒900~‒1150 mV，以此电位分布作为杂散电流干扰研究的基准线。

图4 无地铁杂散电流时被保护埋地管道的保护电位分布

3.2 机车运行状态的影响

设定埋地管道与地铁线路90°交叉，交叉点位于地铁线路的7.2 km处，未考虑排流网和接地系统作用。分别考虑只有1列机车在不同位置运行和多列机车同时运行时的情形。

3.2.1 单列机车运行位置及电流变化

机车在站与站之间运行时，经历牵引加速、惰性运行和制动减速等3个阶段[17]。在牵引加速阶段，机车电流从0逐渐增大，后降低至0，从而进入惰性运行阶段；在惰性运行阶段，机车电流保持为0；在制动减速阶段，机车电流从0开始反向（变为给原正极馈入电流），反向增大后，降低到0。当电流为1760 A的机车运行至正线的4个牵引区间的中点（即1.8、5.4、9.0、12.6 km处）时，埋地管道的电位分布变化如图5所示，轨道对地电位分布和泄漏电流密度分布如图6所示，其中在1.8 km处同时考虑机车电流反向的制动减速情形。

图5 单列机车运行时埋地管道的电位分布

图6 单列机车运行时轨道对地电位和泄漏电流密度分布

由图5可见，机车运行至1.8、5.4、9.0、12.6 km处和1.8 km处电流反向对应的电位偏移最大位置均在交叉点，偏移量分别为133、50、48、127、‒124 mV，管道电位变化超过20 mV的区域均分布在交叉点附近约2.7 km的区域内。这表明，机车处于不同牵引供电区间、运行电流变化均对管道产生了影响，交叉点处管道所受的影响最大。

由图6可见，机车在某一牵引区间内运行时，由于轨道为焊接轨，其他供电区间的轨道也成为杂散电流的流入流出路径，从而对附近埋地管道产生杂散电流干扰。在交叉点处，杂散电流回流路径最短，成为埋地管道上所受干扰最大的点。管道附近钢轨杂散电流的流入（电流密度为正值）或流出（电流密度为负值）决定了管道电位的负向或正向偏移。

3.2.2 多列机车运行位置及牵引电流变化时

设定轨道上分别有2列机车运行在1.8、5.4 km处，3列机车运行在1.8、5.4、9.0 km处，4列机车运行在1.8、5.4、9.0、12.6 km处，2列机车运行在1.8、5.4 km处（5.5 km处电流反向）以及2列机车运行在1.8、5.4 km处（两处电流均反向）等5种情形。计算得到埋地管道的电位分布变化如图7所示，轨道对地电位和泄漏电流密度分布如图8所示。

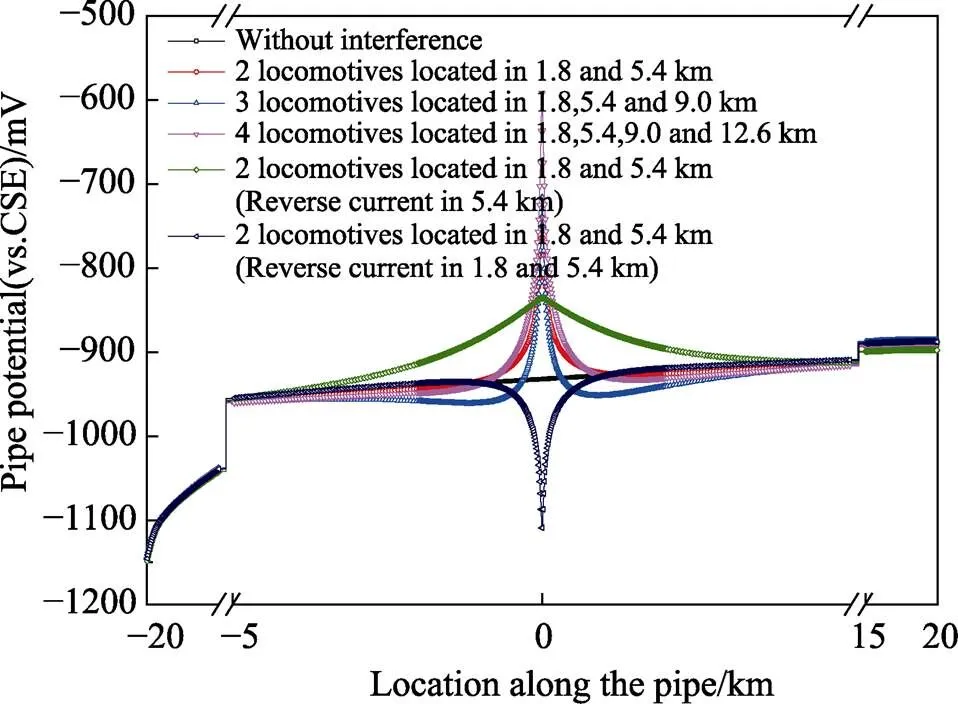
图7 多列机车运行时埋地管道的电位分布

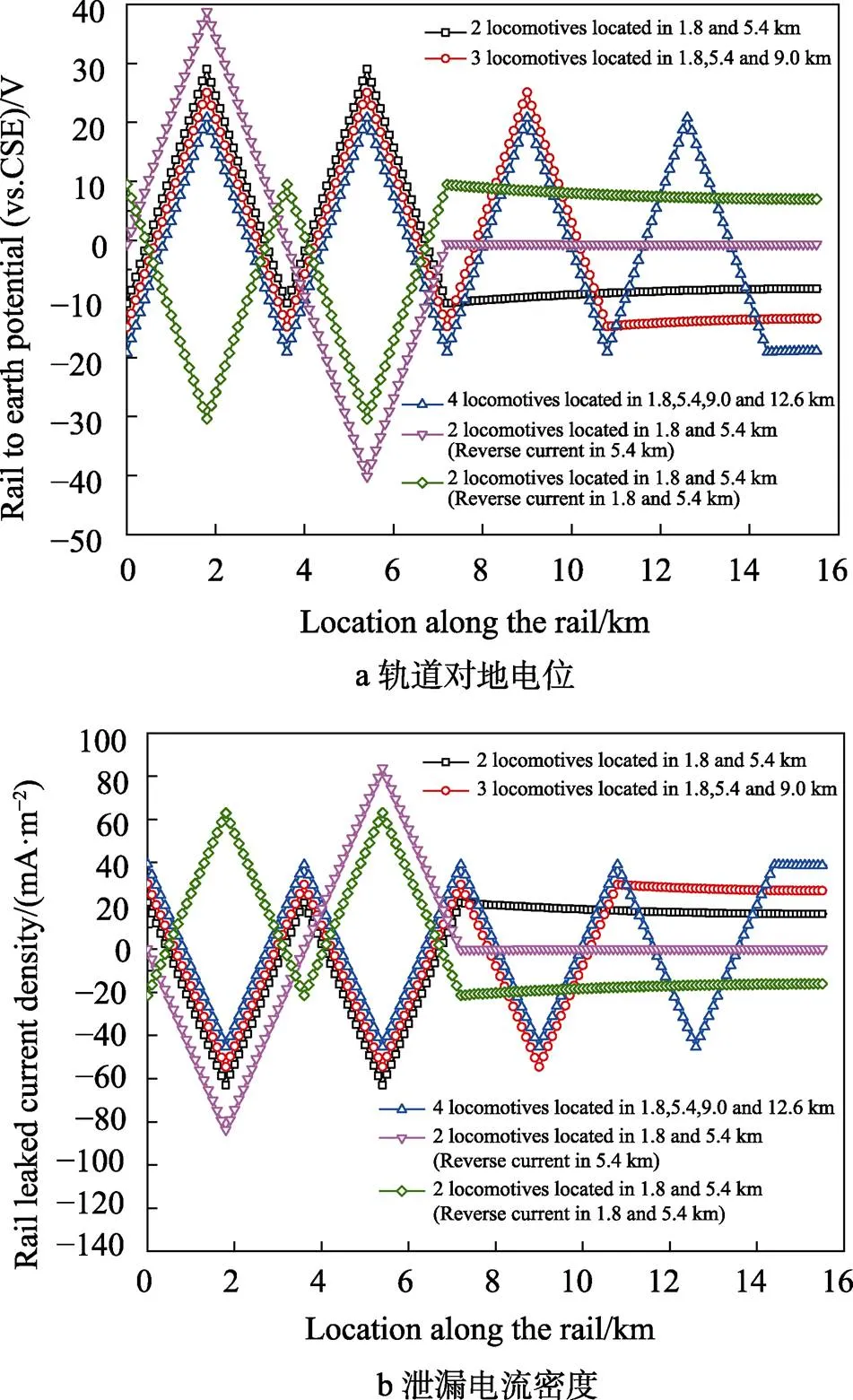
图8 多列机车运行时轨道对地电位和泄漏电流密度分布

由图7可见，上述5种情形对应的电位偏移最大位置也均在交叉点，偏移量分别为193、182、296、96、‒155 mV，约等于单列机车运行时电位偏移之和，即地铁杂散电流干扰有叠加效应，某一处管道所受干扰是所有区间在运行机车共同作用的结果。在上述5种情形下管道电位变化超过20 mV的区域分别分布在交叉点附近约0.8、3.3、1.1、5.0、0.9 km的区域内。这表明，当引起电位偏移方向一致的机车同时运行时，管道附近轨道的杂散电流会增强（如图8所示）。由此引起的管道干扰更加集中，而引起电位偏移方向不一致的机车同时运行时，管道附近轨道的杂散电流会减弱，干扰强度会降低，但干扰影响范围增大。

3.2.3 管道与地铁线路相对位置变化时

当电流为1760 A的机车运行至1.8 km处，管道与地铁线路相对位置变化时，埋地管道的电位分布变化如图9所示。由图9可见，埋地管道与轨道90°和45°交叉时所受干扰水平差距小于1 mV。与线路轨道并行段内，管道所受干扰均较大，且并行间距越小，埋地管道所受的干扰越大，交叉点处干扰水平最大。在并行段，埋地管道所受的干扰水平与交叉时电位衰减至并行间距时的干扰水平差距小于10 mV，因而可利用交叉时的电位衰减预测并行时的干扰大小。由于并行间距越远，干扰水平也越小，因此可合理选择间距来降低干扰水平。

图9 单列机车运行至1.8 km处时埋地管道的电位分布

3.3 地铁排流网工作状况的影响

在地铁高峰运行期间，通常监测到地铁构筑物电位正向偏移电位平均值超过0.5 V时，地铁排流网才与轨道导通而利用排流网回流，从而减少流入流出地铁系统的杂散电流量。当单列机车运行至1.8 km处，在无排流网、有排流网但不与轨道电连接、有排流网且在7.2 km处与轨道电连接以及有排流网与轨道在0、3.6 km处电连接时，埋地管道的电位分布如图10a所示；当有4列机车分别运行至1.8、5.4、9.0、12.6 km处，在无排流网、有排流网但不与轨道电连接、有排流网在牵引变电站与轨道电连接时埋地管道的电位分布如图10b所示。对应的轨道和排流网泄漏电流密度分别如图11a、b所示。

图10 单列和多列机车运行时排流网在不同工作状况下埋地管道的电位分布

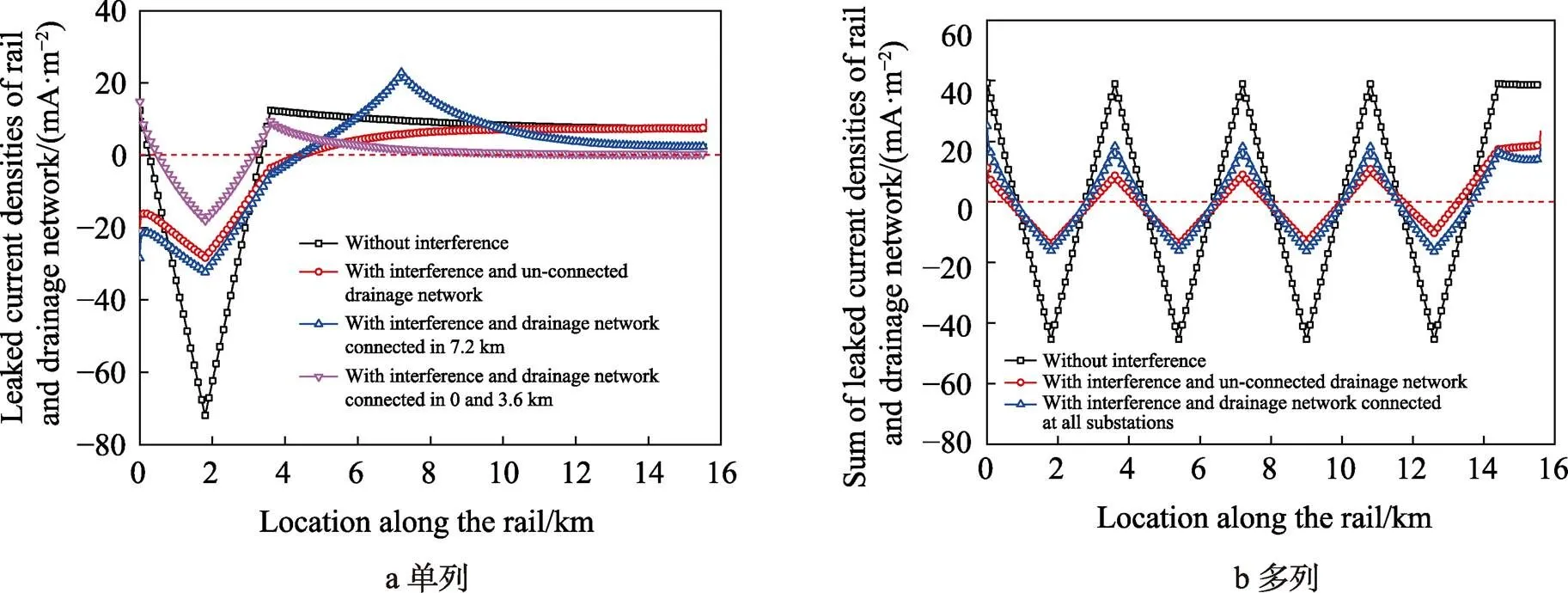
图11 单列和多列机车运行时排流网在不同工作状况下轨道和排流网泄漏电流密度分布

由图10a可见，当排流网在0、3.6 km处电连接（即在有机车运行区间内与牵引变电站电连接）时，埋地管道所受干扰最小。此时排流网收集杂散电流的效果最好，地铁各处对外泄漏的电流密度均较小，如图11a所示。若排流网在轨道与埋地管道的交叉点7.2 km处与轨道电连接时，连接点附近的杂散电流量反而增大，造成埋地管道所受干扰增大。当排流网与轨道未电连接时，地铁各处对外泄漏的电流密度均减小，越靠近机车运行位置，其减小程度越明显，如图11b所示。由此对埋地管道所受干扰也有减小的作用。

考虑到排流网的上述影响规律，在多列机车运行时，为了降低地铁各处泄漏的杂散电流，杂散电流排流网应不与轨道相连或者在每个牵引变电站与轨道相连。由图10b可见，当排流网对地过渡电阻为0.1 Ω·km时，在排流网不与轨道连接或者在每个牵引变电站与轨道相连下，埋地管道干扰均减小。其中排流网不与轨道连接产生的效果更佳，对外泄漏的杂散电流量也最小，如图11b所示。这是因为排流网不与轨道连接时，轨道泄漏的杂散电流量由27.70 A增加28.30 A；当排流网与轨道相连时，杂散电流泄漏量增加到96.22 A，从而导致整体效果变差。

3.4 地铁站接地系统工作状况的影响

当单列机车运行至1.8 km处，在计算模型中分别考虑无接地系统、各站接地系统相互未电连接且不与轨道连接、各站接地系统相互未电连接而7.2 km处站接地与轨道连接、相邻接地系统通过电阻为0.2 Ω电缆连接但不与轨道连接以及相邻接地系统通过电阻为0.2 Ω电缆连接但在7.2 km处与轨道电连接，共5种情形。由此计算获得的埋地管道的电位分布如图12所示，轨道对地电位和泄漏电流密度分布如图13所示、各站接地系统泄漏杂散电流量如图14所示。

由图12可见，当接地系统相互间采用电阻为0.2 Ω电缆连接，且7.2 km处站接地与轨道相连时，埋地管道受干扰的最正电位由‒796 mV增加到612 mV；当接地系统相互不连接，但7.2 km处站接地与轨道相连时，埋地管道受干扰的最正电位由－796 mV增加到1693 mV。由图13可见，在7.2 km处站接地与轨道连接时，轨道对地电压接近自然电位，泄漏电流密度降低接近0。由图14可见，两种情况下对应的7.2 km处站接地系统泄漏电流增加到约4 A和5.5 A，从而造成干扰的增大。当模型中增加接地系统但相互不连接或由0.2 Ω电缆连接时，只要不与轨道连接，埋地管道所受干扰均有减小，最大的电位变化分别为4 mV和34 mV。

图12 单列机车运行至1.8 km处在不同接地状况下埋地管道的电位分布

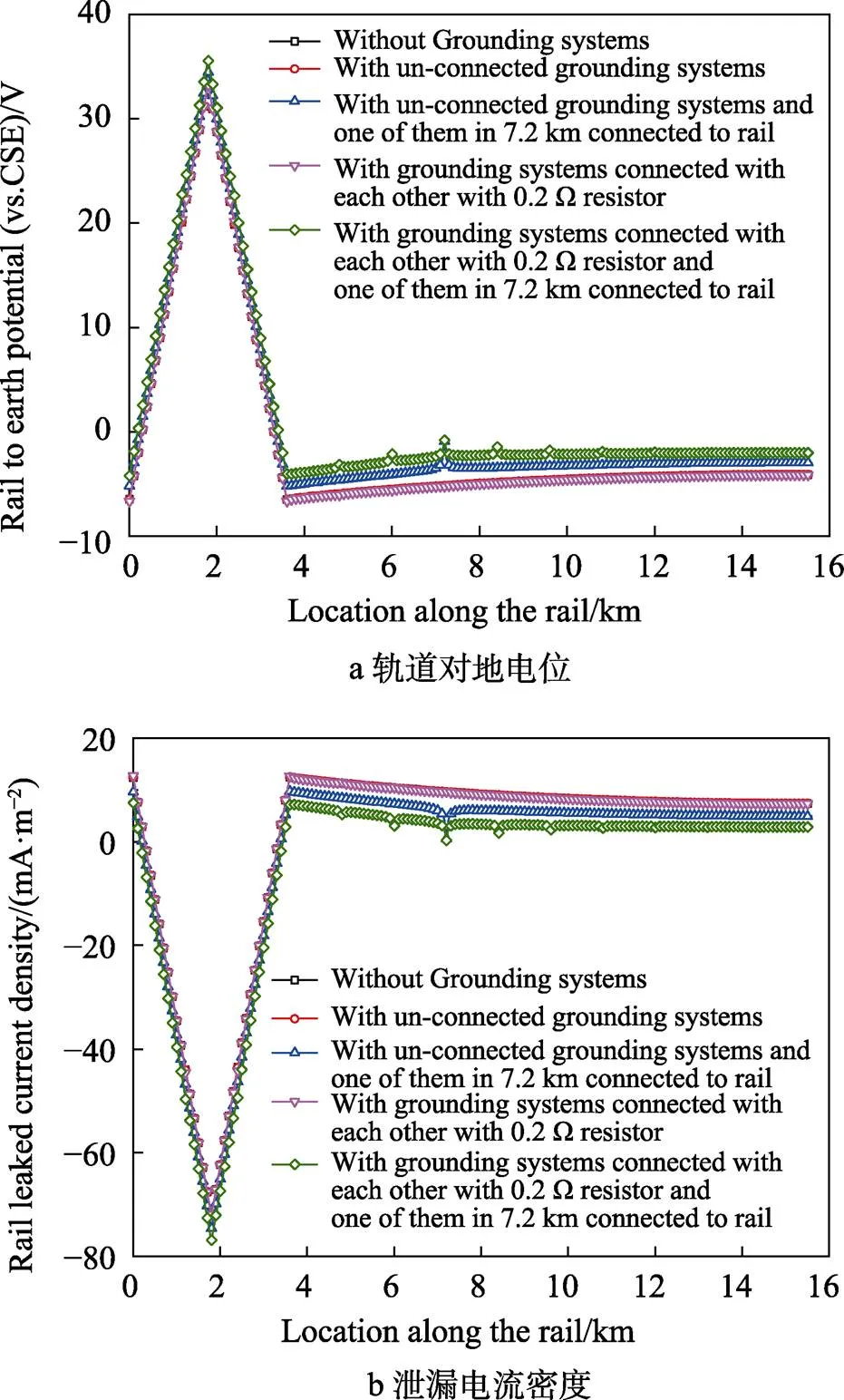
图13 单列机车运行至1.8 km处在不同接地状况下轨道对地电位和泄漏电流密度分布

由图13可以看出，接地系统不与轨道连接时，对轨道对地电位和泄漏电流密度影响较小。由图14可以看出，接地系统相互连接时，会吸收部分杂散电流，该电流总是与轨道泄漏杂散电流方向相反，因而对外泄漏的杂散电流密度降低，从而减小了干扰。

图14 单列机车运行至1.8 km处在不同接地状况下各站接地系统电流

3.5 地铁停车场工作状态的影响

当单列机车运行至1.8 km处，在计算模型中分别考虑了线路轨道与停车场轨道未电连接和电连接两种情况。此时处于7.2、15.6 km处埋地管道的电位分布如图15所示，轨道对地电位和泄漏电流密度分布如图16所示。

图15 单列机车运行至1.8 km处在不同接地状况下埋地管道的电位分布

由图15可见，当线路轨道与停车场轨道由未电连接变为电连接时，7.2 km处埋地管道所受干扰水平降低，而15.6 km处埋地管道所受干扰水平增加。由图16可见，当线路轨道与停车场轨道由未电连接变为电连接时，轨道对地电位整体正移，无机车运行区间轨道泄漏的杂散电流降低，靠近停车场处线路轨道泄漏的杂散电流降低量达到最大，此时停车场泄漏的杂散电流为1.32 A。由此造成远离停车场无机车运行区间的干扰减小，而靠近停车场处埋地管道干扰增大。这表明停车场内轨道集中会造成杂散电流的集中，从而增大附近埋地管道的干扰水平。

图16 单列机车运行至1.8 km处在不同接地状况下轨道对地电位和泄漏电流密度分布

4 结论

1）由于地铁轨道为焊接轨，当地铁采用走行轨回流时，任何牵引供电区间内运行的机车及电流变化均会对靠近地铁线路的埋地管道造成干扰影响。当地铁排流网、站接地系统和停车场轨道不与线路轨道电连接时，与轨道交叉的埋地管道在交叉点处干扰最大，与轨道并行的埋地管道在并行段干扰较高，且并行间距越小，干扰越大。

2）当地铁排流网不与线路轨道电连接时，能够降低对外系统的杂散电流干扰，且排流网对地过渡电阻越小，缓解效果越好。当地铁排流网与机车运行的牵引变电站的轨道电连接时，能够整体降低对外系统杂散电流的干扰水平。当连接点不在机车运行的牵引变电站附近，而是在管道与轨道交叉点时，反而会增大埋地管道所受的干扰水平。因此，排流网在实际运行时，应全部连接牵引变电站处轨道或者均不连接，后者由于不会明显增加泄漏的杂散电流量，因而排流效果优于前者。

3）若埋地管道靠近地铁站，当站接地系统由于人身安全等原因与轨道电连接时，会大幅度地增大埋地管道所受的干扰水平。当停车场轨道与线路管道电连接时，会增大停车场附近埋地管道所受干扰水平。

4）埋地管道所受地铁杂散电流干扰水平与地铁系统运行工况及其与地铁系统的相对位置息息相关。在选址上，应尽量避免二者相互靠近；在防护上，应充分考虑地铁系统的运行工况，尽量避免多列机车运行时牵引电流均正向或负向变化，避免地铁站接地系统或停车场轨道频繁与线路轨道电连接。建议排流网对地过渡电阻要尽可能地小，且不与轨道电导通，从源头上降低埋地管道所受杂散电流干扰水平，降低后续干扰缓解难度。

[1] 韩宝明, 陈佳豪, 杨运节, 等. 2019年世界城市轨道交通运营统计与分析综述[J]. 都市快轨交通, 2020, 33(1): 4-8. HAN Bao-ming, CHEN Jia-hao, YANG Yun-jie, et al. Statistical analysis of urban rail transit operation in the world in 2019: A review[J]. Urban rapid rail transit, 2020, 33(1): 4-8.

[2] 曹阿林, 朱庆军, 侯保荣, 等. 油气管道的杂散电流腐蚀与防护[J]. 煤气与热力, 2009, 29(3): 6-9. CAO A-lin, ZHU Qing-jun, HOU Bao-rong, et al. Stray current corrosion on oil and gas pipeline and its protection[J]. Gas & heat, 2009, 29(3): 6-9.

[3] 金醒群. 地铁杂散电流对埋地钢质燃气管道的腐蚀[J]. 煤气与热力, 2012, 32(3): 31-34. JIN Xing-qun. Corroson of subway stray current on buried steel gas pipeline[J]. Gas & heat, 2012, 32(3): 31-34.

[4] CHEN Z P, KOLEVA D, VAN B K. A review on stray current-induced steel corrosion in infrastructure[J]. Corrosion reviews, 2017, 35(6): 397-423.

[5] 张开宇, 孙齐磊, 种溪, 等. 杂散电流下新型阻锈剂对混凝土中氯离子扩散的影响[J]. 装备环境工程, 2020, 17(4): 90-95. ZHANG Kai-yu, SUN Qi-lei, ZHONG Xi, et al. Effect of new rust inhibitor on chloride diffusion in concrete under stray current[J]. Equipment environmental engineering, 2020, 17(4): 90-95.

[6] 朱祥剑, 杜艳霞, 覃慧敏, 等. 地铁杂散电流干扰下埋地管道管地电位动态波动规律[J]. 腐蚀与防护, 2019, 40(12): 878-885. ZHU Xiang-jian, DU Yan-xia, QIN Hui-min, et al. Dynamic fluctuation characteristics of pipe-to-soil potential on buried pipelines under interference of stray current from subway[J]. Corrosion & protection, 2019, 40(12): 878-885.

[7] 刘杰, 杜艳霞, 覃慧敏, 等. 地铁杂散电流对埋地管道的干扰规律[J]. 腐蚀与防护, 2019, 40(1): 43-47+70. LIU Jie, DU Yan-xia, QIN Hui-min, et al. Interference regularity of metro stray current on buried pipelines[J]. Corrosion & protection, 2019, 40(1): 43-47.

[8] QIAN S, CHENG Y. Accelerated corrosion of pipeline steel and reduced cathodic protection effectiveness under direct current interference[J]. Construction & building materials, 2017, 148: 675-685.

[9] 仉洪云, 张辉, 邢琳琳, 等. 杂散电流对埋地燃气管道腐蚀影响研究[J]. 全面腐蚀控制, 2017, 31(11): 75-77+86. ZHANG Hong-yun, ZHANG Hui, XING Lin-lin, et al. Study on effects of stray current on corrosion of buried gas pipeline[J]. Total corrosion control, 2017, 31(11): 75-77.

[10] 刘瑶, 谭松玲, 邢琳琳, 等. 北京埋地燃气管道地铁杂散电流干扰影响现场检测及规律分析[J]. 腐蚀科学与防护技术, 2019, 31(4): 429-435. LIU Yao, TAN Song-lin, XING Lin-lin, et al. Detection and analysis of interference with buried gas pipelines from subway stray current in Beijing area[J]. Corrosion science and protection technology, 2019, 31(4): 429-435.

[11] 李津. 成品油管道杂散电流干扰的防护[J]. 石油化工腐蚀与防护, 2006, 23(2): 35-38. LI Jin. Prevent stray current from affecting product oil pipeline operation[J]. Corrosion & protection in petrochemical industry, 2006, 23(2): 35-38.

[12] 符耀庆, 王秀通, 陈胜利. 南朗段埋地天然气管道杂散电流检测与治理[J]. 表面技术, 2016, 45(2): 22-27. FU Yao-qing, WANG Xiu-tong, CHEN Sheng-li. Stray current detection and treatment for buried natural gas pipeline of Nanlang segment[J]. Surface technology, 2016, 45(2): 22-27.

[13] WU C F, LIU L L, CHEN H Y. Study on pipe interference from stray current of DC light railway[C]// NACE international annual conference. Louisiana: NACE, 2008.

[14] ALLAHKARAM S R, ISAKHANI-ZALARIA M, DERAKHSHANI M, et al. Investigation on corrosion rate and a novel corrosion criterion for gas pipelines affected by dynamic stray current[J]. Journal of natural gas science and engineering, 2015, 26(9): 453-460.

[15] ZAKOWSKI K, DAROWICKI K, ORLIKOWSKI J, et al. Electrolytic corrosion of water pipelines system in the remote distance from stray currents: Case study[J]. Case studies in construction materials, 2016, 4: 116-124.

[16] DELASCASAS R. Dynamic stray current interference testing and mitigation design for a 90-inch water main[C]// NACE international annual conference. Florida: NACE, 2009.

[17] JAMALI S, ALAMUTI M M, SAVAGHEBI M. Effects of different earthing schemes on the stray current in rail transit systems[C]// International universities power engineering conference. Padova: IEEE, 2008.

[18] 吴畏, 刘炜. 地铁车场杂散电流偏大的原因及应对措施探讨[J]. 城市轨道交通研究, 2018, 21(4): 40-42. WU Wei, LIU Wei. Exploration of large stray current in metro depot and countermeasures[J]. Urban mass transit, 2019, 21(4): 46-49.

[19] 黄山山, 贺睿, 陈智敏, 等. 地铁车辆段杂散电流的探讨与分析[J]. 电气化铁道, 2019, 26(4): 46-49. HUANG Shan-shan, HE Rui, CHEN Zhi-min, et al. Discussion and analysis of stray current in metro depot[J]. Electric railway, 2019, 26(4): 46-49.

[20] 董亮, 石超杰, 陈树新, 等. 埋地管道受地铁杂散电流干扰的缓解方法及效果数值模拟[J]. 北京交通大学学报, 2020, 44(3): 19-29. DONG Liang, SHI Chao-jie, CHEN Shu-xin, et al. Numerical simulation of mitigation methods and the effects on metro stray current interference on buried pipeline[J]. Journal of Beijing Jiaotong University, 2020, 44(3): 19-29.

[21] 董亮, 姜子涛, 杜艳霞, 等. 地铁杂散电流对管道牺牲阳极的影响及防护[J]. 石油学报, 2016, 37(1): 122-129. DONG Liang, JIANG Zi-tao, DU Yan-xia, et al. Influence and protection of metro stray current on pipeline sacrificial anode[J]. Acta petrolei sinica, 2016, 37(1): 122-129.

[22] 张栋梁, 刘娟, 谢业华, 等. 地铁杂散电流动态分布模型研究[J]. 城市轨道交通研究, 2017, 20(4): 76-80. ZHANG Dong-liang, LIU Juan, XIE Ye-hua. Evaluation and analysis of dynamic stray current in DC metro system[J]. Urban mass transit, 2017, 20(4): 76-80.

[23] 胡宏亮, 王崇林, 张栋梁, 等. 城市轨道交通系统杂散电流的分布规律研究[J]. 都市快轨交通, 2005, 18(5): 31-33. HU Hong-liang, WANG Chong-lin, ZHANG Dong-liang, et al. An analysis on the distribution regularities of stray current in urban rail transit system[J]. Urban rapid rail transit, 2005, 18(5): 31-33.

[24] 杜艳霞, 张国忠, 刘刚, 等. 金属储罐底板外侧阴极保护电位分布的数值模拟[J]. 金属学报, 2007, 43(3): 297-302. DU Yan-xia, ZHANG Guo-zhong, LIU Gang, et al. Simulation of cathodic protection potential distribution on the exterior of storage tank bottom[J]. Acta metall sin, 2007, 43(3): 297-302.

[25] JIA J X, SONG G, ATRENS A, et al. Evaluation of the BEASY program using linear and piecewise linear approaches for the boundary conditions[J]. Materials and corrosion, 2004, 55(11): 845-852

[26] BS/ISO 15589-1—2015, Petroleum, petrochemical and natural gas industries—Cathodic protection of pipeline systems Part 1: On-land pipelines[S].

[27] 徐霞, 刘熙, 刘刚, 等. 典型地区土壤电阻率的时空特性研究[J]. 水电能源科学, 2017, 35(2): 204-207. XU Xia, LIU Xi, LIU Gang, et al. Study on spatiotemporal property of soil resistivity in typical regions[J]. Water resources and power, 2017, 35(2): 204-207.

Numerical Simulation of Stray Current Interference Rules on Buried Pipeline from Metro System under Different Operative Modes

DONG Liang, CHEN Jin-ze, YAO Zhi-lin, SHI Chao-jie

(School of Petroleum Engineering, Changzhou University, Changzhou 213164, China)

Stray current interference on nearby buried pipeline from metro system under variable operating conditions is complicated, so that the interference rules are difficult to obtain through field tests. In this paper, a numerical simulation model including an entire metro system with multiple traction sections, drainage network, grounding systems in stations and a parking lot, the buried pipeline and its cathodic protection system are constructed. Based on the numerical simulation method and professional software, the potential distribution of rail to earth, the leakage stray current density distribution from rail and drainage network, the stray current flow of grounding systems and a parking lot, and the potential distribution of buried pipeline under stray current interference are calculated under different metro operating conditions such as changes of the number, location and traction current of metro locomotives, the electric connections of drainage network, grounding systems and rails in the parking lot with the main track. The interference rules of stray current on buried pipeline from metro system under different operating conditions are determined. The results show that stray current interference on nearby buried pipeline occurs and is superposed from multiple traction sections with running locomotives. The maximum interference occurs at the intersection or parallel section of the buried pipeline and the track, and the smaller the parallel distance is, the closer the maximum interference level is to the interference level at the intersection. When the drainage network, grounding system in stations and parking lot track are not electrically connected with the main track, the interference level can be reduced to a certain extent. However, when the drainage network, grounding system in stations or/and parking lot track is locally electrically connected with the track, the interference level on buried pipeline will increase dramatically. The potential fluctuation of buried pipeline is caused by the change of metro operating condition, and the fluctuation degree is closely related to the running state of locomotives, the electric connection state of rail with grounding system or parking lot, the performance of drainage network and its working state, etc. Therefore, attention should be paid to the change of metro operating condition in metro stray current interference detection and protection.

metro system, stray current, influence laws, numerical simulation, buried pipeline, operating condition

2020-10-11；

2020-11-14

DONG Liang (1983—), Male, Doctor, Senior engineer, Research focus: corrosion and protection.

董亮, 陈金泽, 姚知林, 等. 地铁运行状态变化下杂散电流对埋地管道干扰数值模拟[J]. 装备环境工程, 2021, 18(4): 033-042.

TG172.84

A

1672-9242(2021)04-0033-10

10.7643/ issn.1672-9242.2021.04.005

2020-10-11；

2020-11-14

国家自然科学基金（51401017）

Fund：Supported by National Natural Science Foundation of China (51401017)

董亮（1983—），男，博士，高级工程师, 主要研究方向为腐蚀与防护。

DONG Liang, CHEN Jin-ze, YAO Zhi-lin, et al. Numerical simulation of stray current interference rules on buried pipeline from metro system under different operative modes[J]. Equipment environmental engineering, 2021, 18(4): 033-042.