改进LSTM神经网络在电机故障诊断中的应用

张 凯，林谷烨，罗 权

(华南理工大学 电力学院，广州 510000)

0 引言

伴随着人工智能领域的发展，越来越多的传统领域开始尝试采用神经网络理论来解决工程实践中难以精确建立数学模型的问题。异步电动机由于具有故障种类较多，受外界干扰大等特点，而传统基于建模分析的方法难以建立适应各个复杂场景下的三相异步电机运行时的数学模型，所以使用神经网络进行故障诊断分析相比于传统的电机建模分析等方法有着得天独厚的优势。目前国内外也已经有一些研究采用神经网络进行电机故障诊断的研究[1-3]。但是目前采用的方法仍然存在一些不足：首先，基于模型的方法虽然精度高，但计算量大，且难以得到精确的模型；其次，对于传统的神经网络模型存在无法排除扰动，收敛精度不足或者无法保证收敛等问题。

在这样的背景下，本文基于最新提出的RAdam优化器构建LSTM神经网络，相比于传统的神经网络而言：1)LSTM神经网络的网络结构更适合进行时序自回归预测[4]；2)使用RAdam优化器解决了传统神经网络模型在训练的初期学习率的方差较大、收敛速度较慢、收敛精度较低等问题；3)针对输出精度较低以及模型易受干扰等问题[5-6]，采用双峰插值法[7]进行滑窗滤波，并采用时间序列进行输入以提高精度。

1 双峰谱线插值与滑窗法提取谐波

在实际工业场景下，由于电网电压存在波动等情况，导致三相异步电机在运行过程中无法针对一个长的时间序列进行高精度的谐波分析，所以在实际应用中采用滑窗法对实际运行的波形进行分段分析[8]。

1.1 双峰谱线插值算法

假设含有H次谐波分量的信号x(t)经过采样频率为f(s)的均匀采样后得到如下形式的离散时间信号：

(1)

式中，H为谐波次数;当i=1时,A1、f1和θ1分别为基波的幅值、频率和相位；当i≠1时，Ai、fi和θi分别为第i次谐波的幅值、频率和相位。

对式(1)的信号加窗处理后的离散傅立叶变换表达式为：

(2)

式中，Δf=fs/N为采样频率分辨率；k为采样序号；N为数据截断长度。

忽略其他谐波对第i次谐波的泄露影响以及负频点-f1处频峰的旁瓣影响，并有rif1=kioΔf,假设要求解的是第i次谐波分量，则有：

(3)

由于实际采样时会出现采样周期非整数次以及采样非同步而导致频谱泄露，所以ki0一般不为整数。设峰值点左右两侧的谱线为第ki1和ki2，则有ki1≤ki0≤ki2=ki1+1。引入参数α=ki0-≤ki1-0.5且α∈[-0.5，0.5]，并设β=(y2-y1)/(y2+y1)，并由式(3)可得：

f(α)

(4)

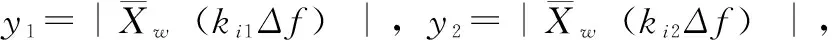
采用余弦组合窗函数，并计算可得：

(5)

α=f-1(β)≈

a1·β+a3·β3+…+a2/l+1·β2/l+1

(6)

由α可求得第i次谐波的频率修正公式、谐波相位修正公式分别为：

fi=ki0Δf=(α+ki1+0.5)Δf

(7)

针对t=1,2两种情况的结果进行加权平均最终可得到相位修正公式：

θi=θi1·(α+0.5)+θi2·(-α+0.5)

(8)

第i次谐波的幅值修正是对第ki1和ki2根谱线取加权平均，其计算公式为：

Ai=

(9)

1.2 滑窗法提取基波

在双峰谱线插值算法的基础上，针对时间跨度较大的波形采用分段滑窗求取整个时间域上精确的谐波。

图1为利用双峰插值和滑窗法提取基波的示意图。

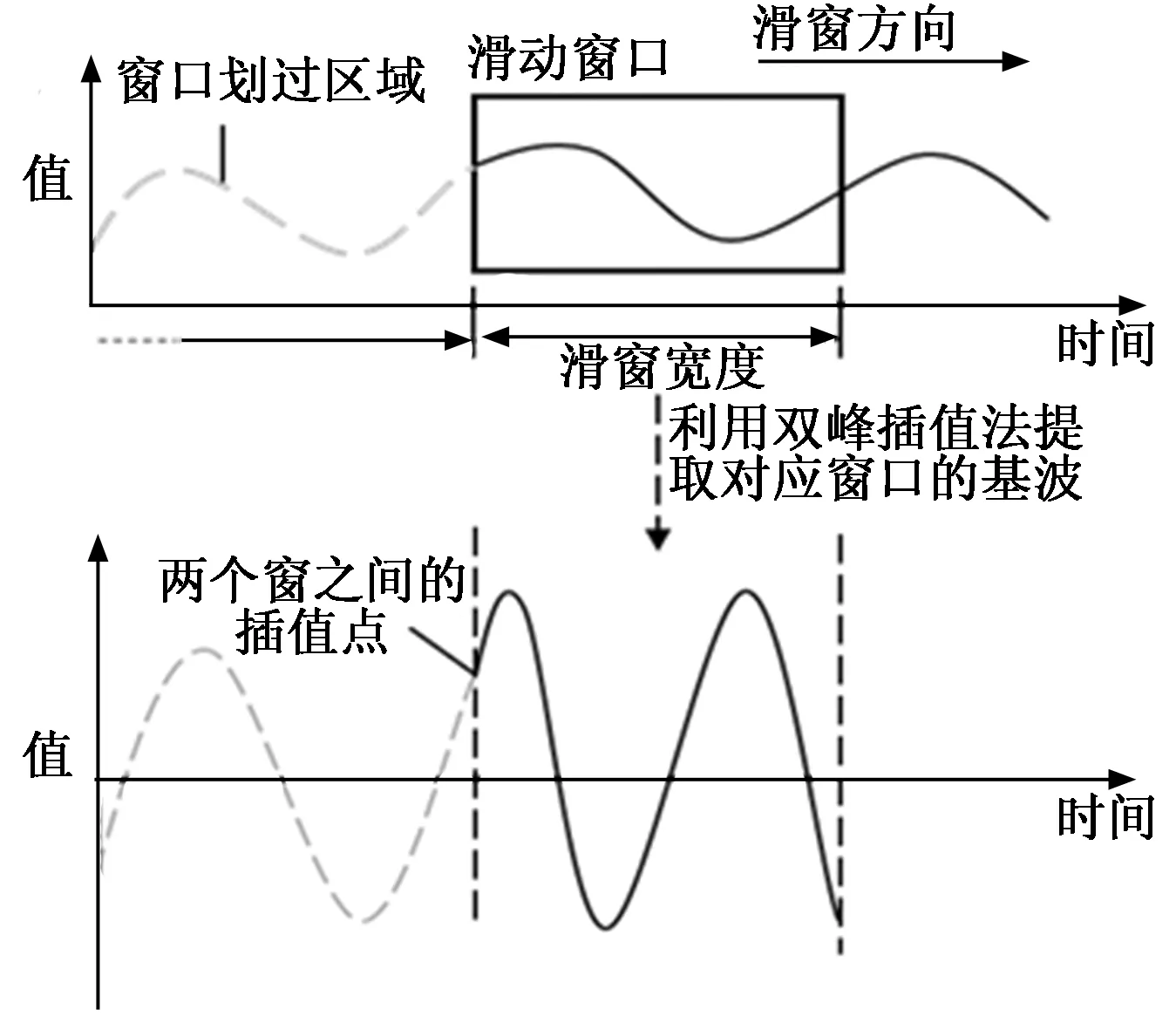
图1 滑窗法提取基波原理图

对于相邻的两个窗之间需要进行插值运算，设第i个插值点左侧的基波幅值、频率以及相角为A1、f1、θ1，插值点右侧的基波幅值、频率以及相角为A2、f2、θ2，且插值点所在时刻为ti，则根据左右两侧极限的平均值可得插值点的值为：

(10)

由式(7)～(10)推广至整个采样时间域，并设采样起始时刻为t0，采样终止时刻为tn窗口大小为ΔT，则经过双峰插值与滑窗法提取后的采样波形的时间域函数φ(t)表达式为：

(11)

其中：

(12)

1.3 实际数据处理效果

以实验时A相电压为例，采样频率为8 000 Hz，采样时间为10 s，则使用滑窗法和不使用滑窗法提取并去除基波后的谐波波形与频谱如图2所示。

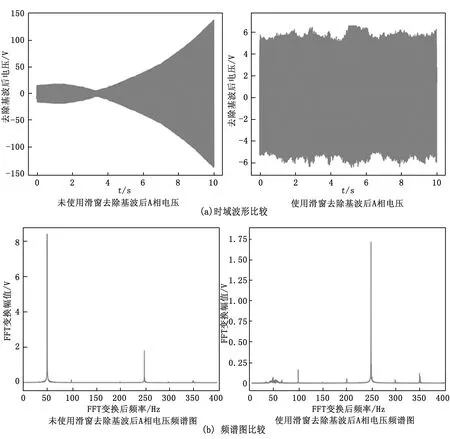
图2 滑窗法与不使用滑窗法在时域与频域的对比图

从图2可以看出,由于电网电压的基频是随时间波动的，所以如果不使用滑窗法从一个小窗口提取基波将会造成很大的误差。在频谱图中也说明了使用滑窗法提取并去除基波时可以很好地动态跟踪电网基频的变化，而不使用滑窗法则会受到电网电压基频波动的影响。

2 改进LSTM神经网络的时序预测模型

2.1 LSTM神经网络与RAdam优化器

LSTM神经网络是一个深度学习网络，被设计为学习长期依赖关系。通过引入特殊类型的门来实现长期保存信息。遗忘门可以丢弃冗余信息；输入门可以选择要存储在内部状态的关键信息；而输出门用于识别输出信息。

通常，LSTM神经网络训练采用Adam优化器，是由Kingma和Lei Ba两位学者提出的结合AdaGrad和RMSProp两种优化算法的优点的优化器。对梯度的一阶矩估计(first moment estimation，梯度的均值)和二阶矩估计(second moment estimation，梯度的未中心化的方差)进行综合考虑，计算出更新步长。

虽然Adam优化器中加入了一阶矩估计和二阶矩估计可以产生自适应式的学习率从而加速了收敛过程并提升了model的泛化能力。但是由于在训练的初期，训练数据较少，此时学习率的方差大，不确定性因素较多，所以会使得训练初期不太稳定，进而导致模型训练时陷入局部最优解。常用解决Adam收敛问题的方法有：采用自适应启动方法；指数加权平均的启发式warmup算法等。

而RAdam(Rectified Adam)优化器在其导数的基础上，通过估算自由度来实现自适应的学习率，并进行显式地修正。RAdam算法的输入有：步长αt；衰减率{β1，β2}用于计算移动平均值和它的二阶矩。

首先，初始化移动量的一阶矩m1和二阶矩m2并估算简单移动平均值(SMA)的最大长度ρ∞=2/(1-β2)-1;

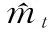
(13)

移动偏差经过计算之后再针对ρt判断步长的稳定度：

如果ρt>4则进行自适应动量来更新参数。移动二阶矩的修正值和方差修正值为：

(14)

此时的模型参数迭代规则如下：

(15)

如果ρt≤4，则使用非自适应动量更新参数：

(16)

输出为θt表示第t步后的模型参数。

2.3 LSTM神经网络进行时序预测的原理

时序预测建模是使用现有的数据来建立未来数据的模型。建模的前提是所要预测的时间序列是一个稳定的、可预测的序列，通常也称为自回归(AR，autoregressive)预测，其表达式如下：

(17)

式中，c是常数项，φi是建模参数，εt是随机误差值。则基于此模型扩展的神经网络自适应学习算法的公式如下所示：

xt=f(xt-1,xt-2,…，xt-n)t∈(n+1,k)

(18)

本文采用LSTM神经网络建立k-n数据集的训练模型，即得到网络f。与传统的神经网络不同，LSTM神经网络在训练阶段不是独立的，网络不是直接从当前时刻t开始训练，而是从以前的训练结果0到t-1继续训练，充分利用了时间序列的时间连续性。LSTM网络训练模型时，以xt-1为输入，xt为回归数据的输出。

最后，在进行训练之前对LSTM神经网络结构进行构建。神经网络的层结构如表1所示。整个神经网络由一个多维向量的输入层，多个LSTM和Dropout组成的中间层和一个回归输出层组成。其中加入Dropout层是避免模型出现过拟合问题。

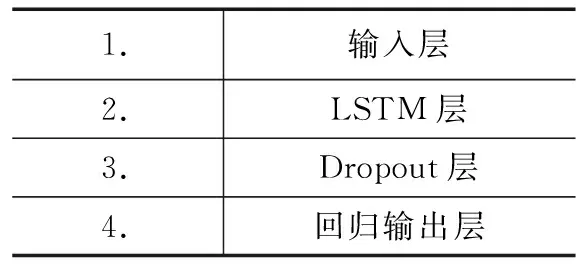
表1 时间序列的LSTM模型

3 利用LSTM神经网络进行电机故障诊断

3.1 电机故障诊断的原理

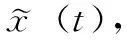
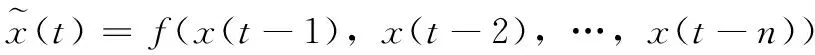
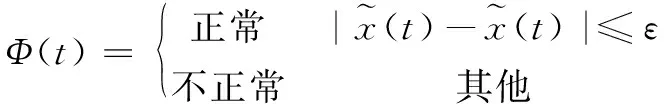
(19)

其中:f是2.3小节所述的时间序列模型，ε为允许误差范围，Φ(t)为校验函数。

在实际应用中，采用电网三相电压以及运行时三相电流作为整个LSTM网络的输入。针对电网中基波数值较大导致在训练时无法正确捕捉电网谐波，从而无法正确预测在特定电网谐波下电机实际运行特性的问题[10-12]，文章提出采用1.2小节中所述的方法，训练时采用滑窗法处理后的电网三相电压的谐波以及电机实际运行时的三相电流的基波作为输入向量，并且以三相电流的实际波形作为输出，并且将预测理论值的频谱与实际采样时的电流频谱作对比，并利用特征电流法理论对比两电流的实际频谱，便可得出实际电机有无故障以及故障类型。

同时，传统的训练方法采用单个输入参数进行训练，鲁棒性较差。而在本文中对此方法进行了改进，采用6×n的向量形式作为层内数据，以提取数据特性，如图3所示。

图3 LSTM神经网络滑窗算法

3.2 故障诊断的算法流程

电机故障诊断算法分为模型训练和模型预测与故障诊断两个部分。整个算法的流程如图4所示。

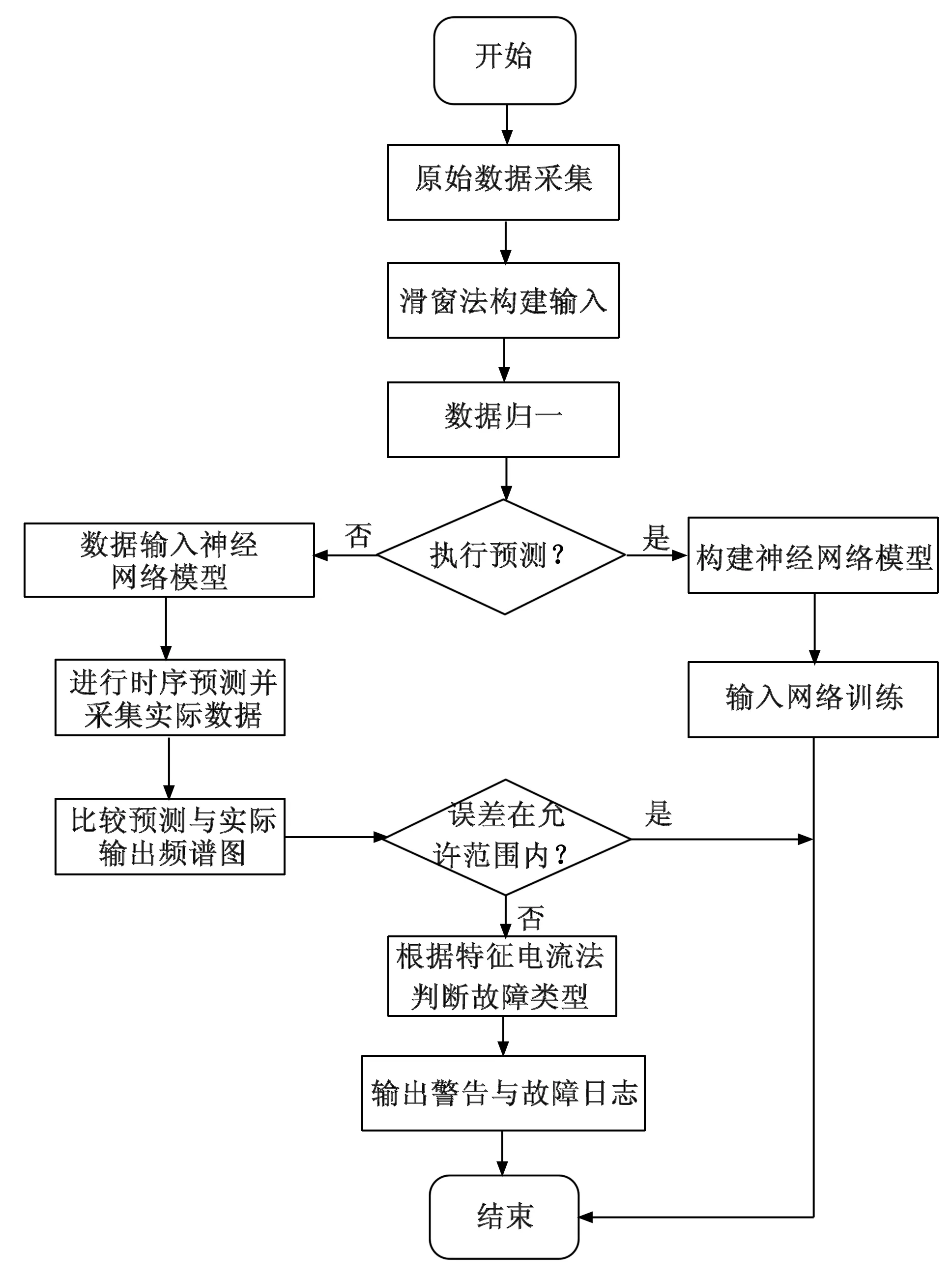
图4 故障识别算法流程图

通过训练数据集，得到了一个LSTM模型。当模型遇到正常工作数据时，它能在下一时刻精确地预测参数。当出现异常状态时，预测结果会偏离实际值，从而判断故障的发生。并通过将故障频谱与正常运行时频谱进行比较，基于特征电流法可以判断出故障类型。

4 实际算例分析

4.1 故障诊断系统

为了获得待测电机分别在各种故障情况下的定子电流，需要搭建电机故障监测实验平台。

实验平台的结构如图5(a)所示。图中M为待测异步电机，G为发电机，R为水阻箱，G和R组成待测电机的负载。利用电机信号采集仪，监测并采集定子电信号，将采集到的信号上传至上位机中，由上位机内置的故障诊断系统进行数据分析与故障识别。图5(b)为感应电机信息采集分析系统示意图。

图5 故障诊断系统实验示意图

考虑到实验电机的选型要满足易发生高频故障，又考虑到价格需要在实验成本之内。本次实验选择一台低压电机作为实验的待测电机，电机铭牌参数如表2所示。

表2 实验电机铭牌参数

对于信号采集单元，本文实际监测设备接线如图6所示。

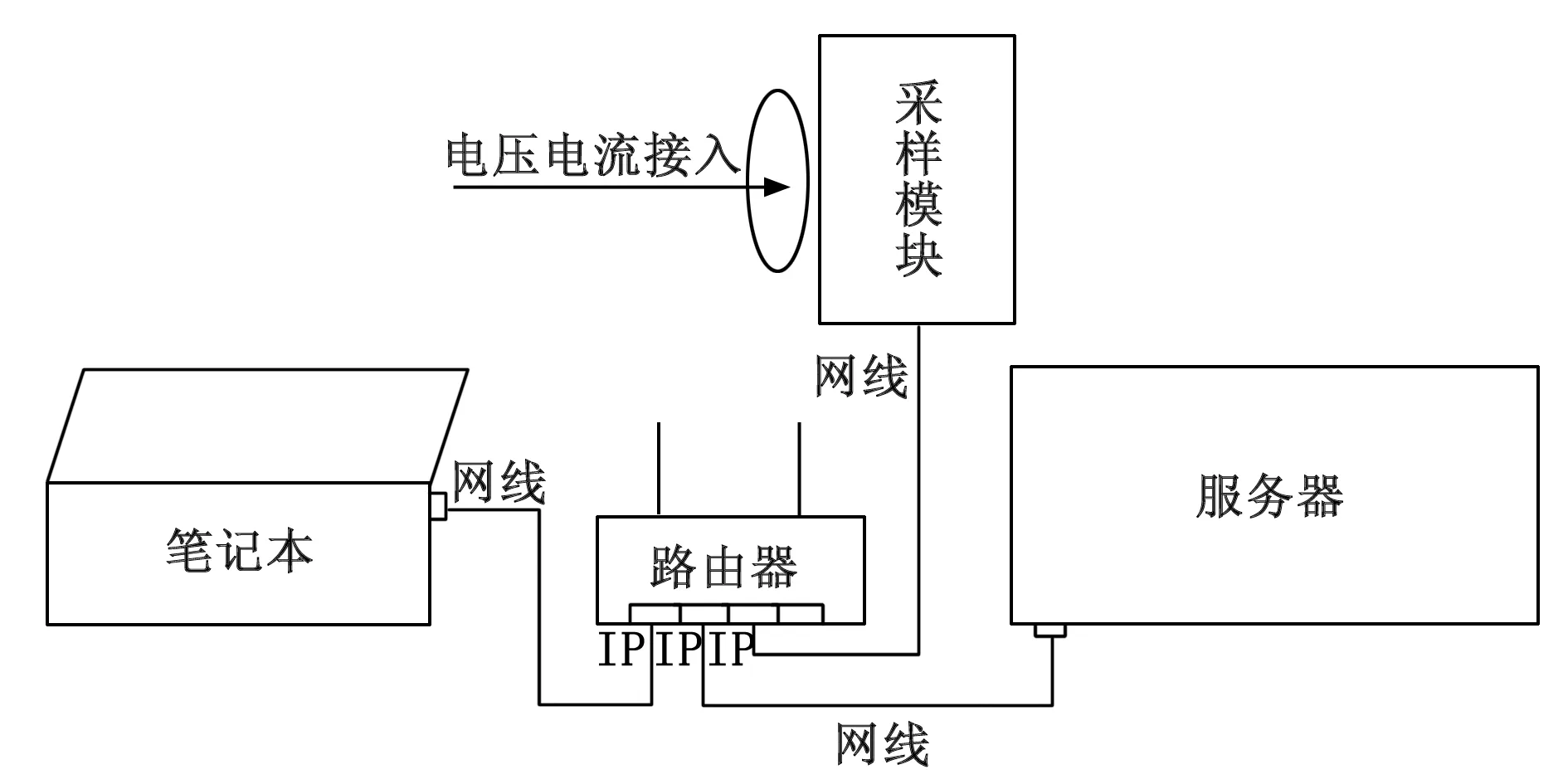
图6 监测设备接线示意图

采样模块通过网线连接至局域网的电脑，即可实时获得测量的数据。采样模块拥有7个通道接入测量数据，本文采用其三相电压、电流作为实验测试。其中电压变比kU=5 928 256*515，电流变比kI=5 928 256*10.31。采样频率为8 kHz，即每个周波160个点。采样设备内部基于UDP通信协议并以Modbus隧道的通信方式将电压、电流波形数据向外发送。

本文针对异步电机运行时最经常出现的偏心故障进行实验，分别测取各型号电机在正常运行以及人为制造偏心故障时的运行数据。其中，人为制造偏心故障的方法是：打磨电机端盖一侧，并在另一侧塞入铜箔，使电机转子斜偏心，偏心约10丝(1丝=0.01 mm)，处理结果如图7所示。

图7 气隙偏心的实现

经过试验后，针对电流数据过滤出整数次谐波，并做傅里叶分析，可得如图8所示的偏心故障局部特征频谱图。

图8 22 kW偏心故障局部特征频谱图

由图8可见，当异步电机发生静态偏心故障时，定子电流出现频率为99.5 Hz的边频带。通过传感器测速得电机发生断条故障时的转速n=2 970 r/min，转差率s=0.01。根据特征电流法理论分析[13]，定子电流的边频带频率应为:

(2-s)f1=(2-0.01)*50=99.5 Hz

(20)

实验结果与理论分析完全一致。

4.2 与传统神经网络预测对比

为验证所提出的基于RAdam优化器的LSTM算法的有效性，选择了经典的BP网络、标准的LSTM神经网络、采用RAdam优化器的LSTM神经网络以及经过数据预热的RAdam优化器的LSTM神经网络进行比较。其中BP网络结构，以及LSTM相关网络的结构如表3所示。

表3 神经网络模型结构

图9 4种网络结构在验证集上的表现

训练数据长度为100 s，采样率8 000 Hz，即800 000个点。使用均方误差(MSE，mean square error)来衡量训练准确性。4种神经网络结构在验证集的比较结果如图9所示。从验证集的结果可以看出，BP网络相较于LSTM网络在频谱预测上存在较大的误差，并且在300 Hz与400 Hz处均存在错误的预测结果。而LSTM网络的预测结果明显更优，并且使用RAdam优化器进行优化的网络具有更好的测试数据集拟合能力。使用Warm-up进行数据预热的结果与使用RAdam优化器的结果极为相似，但是收敛速度更快。

4.3 实际故障诊断效果

故障检测的原理是检测模型中的数据与实际数据之间的差距。通过4.2小节的比较，可以看出RAdam-LSTM方法的时间序列建模更好。因此，本节针对这个方法的故障检测效果进行实验，实验预测结果如图10所示。

图10 基于RAdam-LSTM神经网络进行故障识别

在图10中，展示了基于RAdam-LSTM时间序列模型在故障条件下的实测数据和预测数据。该图显示了电机在发生4.1小节所述的偏心运行情况下的故障识别。当发生故障时，RAdam-LSTM方法在预测值和测量值之间有较大的差距，使得故障得以确定。

5 结束语

本文创新性地将LSTM神经网络应用于三相异步电机的故障检测，通过滑动窗口剔除基波，并建立预测模型。研究结果表明，使用LSTM神经网络进行时间序列建模时，基于RAdam优化器的LSTM神经网络的性能优于传统的神经网络模型。此外，当该方法预测故障实例时，在LSTM网络上应用滑动窗口比传统网络方法提供了更好的分类精度，可以实现更少的训练迭代和更高的精度。最后通过实际数据实验表明此方法具有实际可行性，为之后电机故障诊断提供了新的思路。