基于TensorFlow的LSTM模型在空气质量指数预测的应用*

杨超文 汪宇玲 舒志敏 刘晶晶 谢娜娜

(东华理工大学,江西南昌 330000)

0 引言

近年来,随着南昌经济快速发展,工业化和城市化进程加快,以PM2.5、PM10为主的空气污染也愈加严重,为了人民的健康实现一套对空气质量精准预测的方案刻不容缓[1]。传统预测空气质量的方法很多,如CAPPS模型、灰色模型、人工神经网络(BP)等。Boznar等人将神经网络运用在预测空气质量上,之后最为经典的BP神经网络通过Giusepp等人的改进,进一步提高了预测结果的精度,但BP神经网络较难收敛[2]。后来Fabio Biancofiore等人通过改进采用递归神经网络预测PM10、PM2.5取得了很好的效果,接着Rao等人构建了基于循环神经网络(RNN)的空气质量预测模型,并取得了更高的预测精度。然而RNN运算过程中存在梯度消失、记忆时序数据短等问题,而长短期记忆人工神经网络(LSTM)解决了这些问题,应用在空气质量预测上取得了比RNN更好的结果[3]。因此,本文采用基于TensorFlow的改进LSTM模型来预测南昌市空气质量(AQI)指数。

1 理论介绍

1.1 空气质量指数

空气质量最主要、最常用的衡量指标即AQI(空气质量指数),用来衡量空气清洁或者污染的程度,值越小表示空气质量越好,具体等级划分见表1。参与空气质量评价的主要污染物有六项指标分别为PM10、PM2.5、NO2、SO2、O3和CO。

1.2 数据平稳性与白噪声

时间序列预测模型在平稳数据上进行研究,如果时序数据非平稳,则预测结果误差较大,没有研究价值,因此,建模前需对数据进行平稳性检验,ADF(Augmented Dickey-Fuller test)检验是判断数据平稳的有效方法之一,又称单位根检验。在自回归过程中:yt=byt-1+a+εt,如果滞后项系数b为1,就称为单位根。假如单位根存在,自变量和因变量之间就会具有欺骗性,因为残差序列的任何误差都不会随着样本量增大而衰减,则时间序列是非平稳的。ADF检验的原假设和备择假设如下:

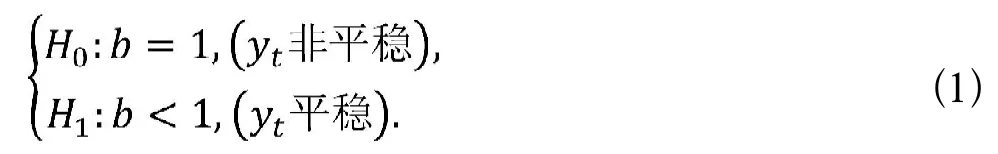
如果显著性检验统计量P值小于0.05,则拒绝原假设,就认为不存在单位根,即时间序列是平稳的。

判断时间序列是平稳之后,就需要检验数据是否为白噪声,白噪声是没有研究意义的。白噪声检验的原理基于Barlett定理:如果一个时间序列是纯随机的,得到一个观察期数为n的观察序列,那么该序列的延迟非零期的样本自相关系数将接近服从均值为零,方差为序列观察期数倒数的正态分布 N(0,1/n),k≠0。白噪声检验的原假设和备择假设如下:

表1 空气质量指数(AQI)分级示意表Tab.1 Air quality index (AQI) classification table

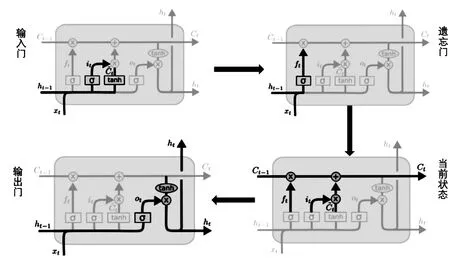
图1 LSTM结构示意图Fig.1 LSTM structure diagram

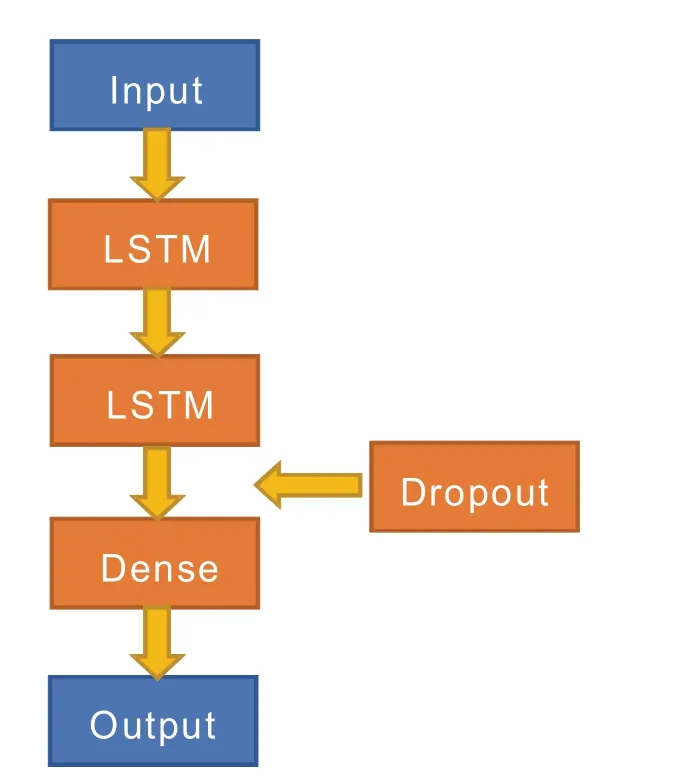
图2 添加了Dropout层的LSTM结构图Fig.2 LSTM structure diagram with dropout layer added

如果显著性检验统计量P值小于0.05,则拒绝原假设,接受备择假设,即平稳时间序列非白噪声。

1.3 LSTM网络理论

LSTM是一种改进的RNN的模型,如图1所示。LSTM 通过增加输入门、遗忘门、输出门以获得变化的自循环权重,在模型参数固定的情况下,不同时刻的积分尺度得以动态改变,从而规避了梯度消失或爆炸的问题[4]。LSTM与RNN的不同就在于存在可以选择性的保留和舍弃一些不重要的序列和拥有自我衡量机制,可以更好地记忆长期序列。

图1中,f(t),i(t), 和o(t)分别表示了在t时刻对应的三种门的结构和细胞状态; 表示矩阵逐点乘法运算; 表示矩阵相加。

LSTM中各参数具体更新过程如下:

其中,f(t)为t时刻遗忘门的输出;i(t)为t时刻输入门的输出;o(t)为t时刻输出门的输出;Wf、Wi、Wc、Wo和bf、bi、bc、bo分别为遗忘门、输入门、细胞状态、输出门对应的系数;σ为sigmoid激活函数;tanh为双曲正切激活函数。

1.4 TensorFlow简介

TensorFlow是谷歌推出的机器学习系统,在深度学习基础架构Dist Belief的基础上推进了一步,其模型简洁,训练速度快,支持GPU和TPU数值计算,是目前主流的用于实现神经网络内置架构的软件库[5]。

2 LSTM空气质量指数预测模型

2.1 数据集的构建与划分

本文空气质量指数预测模型构建了多变量单步LSTM输入数据集,该数据集构建思想为:用n_predictions(时间步长)个小时的各指标x1、x2…xn的值xnt-n_predictions来预测后一个小时的值为第n个指标在t时刻的值,t=[n_predictions+1,…,num-1],num为数据集的行数(即总的小时数据的个数)。这样输入数据集就是(num+n_predictions-1)*n_predictions*n的三维数组,输出数据集就是(num+n_predictions-1)*n的二维数组。

2.2 数据归一化处理

在机器学习中,如果数据之间存在奇异样本数据,可能导致模型很难收敛并使结果的误差变大,为了消除奇异样本数据导致的不良影响以及加快模型收敛速度,需要对数据做归一化处理。本文采用最大最小标准化方法对数据做归一化,将数据转化为[0,1]之间的值。具体公式如下:

其中,Xnorm为归一化后的数据,X为原始数据,Xmax、Xmin分别为原始数据集的最大值和最小值。

2.3 LSTM模型的构建

堆叠式LSTM模型拥有一个或多个隐藏层(LSTM层),各个层都处理模型中的一部分任务,其中上一层解决完相应的任务后把结果传递到下一层,然后依次传递直到传到最后一层输出。本文构建的堆叠LSTM结构如图2所示,由2个LSTM层、Dense层和Dropout层构成。LSTM层太少了得出的结果精度可能不高,太多层会使模型变得过于复杂,模型很难收敛,还会出现过拟合现象。Dense层对高纬信息进行降维处理,同时保留有用信息,最后输出对应目标序列。Dropout层则用来避免过拟合问题。

2.4 反归一化并输出结果

将归一化后的数据带入模型得出的结果是[0,1]范围内的值,若要准确的对模型做出评价,需要将预测到的数据进行反归一化,恢复原来的量纲,然后与原数据按一定的方法进行比较,得出评价模型的系数值。

其中,X为原始数据,Xnorm为归一化后的数据,Xmax、Xmin分别为原始数据集的最大值和最小值。

2.5 模型评价指标

采用相关系数(Correlation coefficient)、斯皮尔曼等级相关(Spearman Rank Correlation)和均方误差(meansquare error,MSE)来评价模型效果。均方误差用来反应预测值与实际值的吻合程度,相关系数和斯皮尔曼等级相关用来反应预测值与实际值之间联系的密切程度。计算公式如下:

表2 AQI、六个污染物ADF检验的P1值以及白噪声的P2值Tab.2 AQI, P1 value of ADF test for six pollutants and P2 value of white noise

图3 AQI指数和六个污染物的相关性分析热力图Fig.3 Thermodynamic diagram of correlation analysis between AQI index and six pollutants

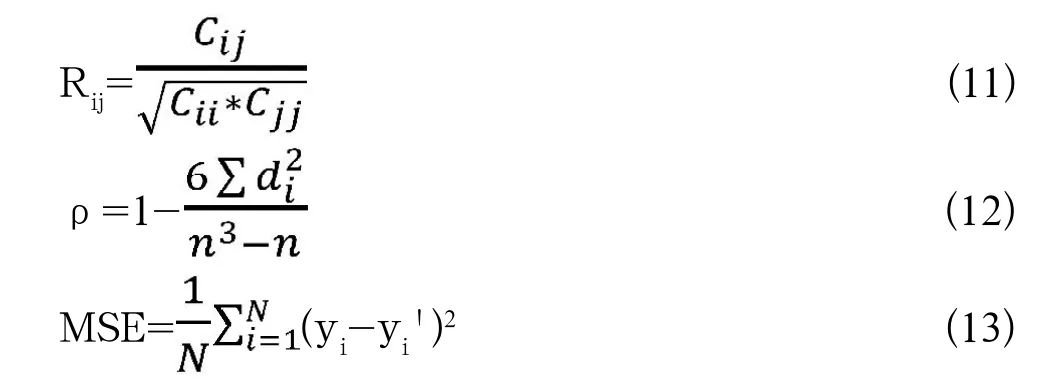
其中R为相关系数;C为协方差矩阵;ρ为斯皮尔曼等级相关;n为等级个数;d为二列成对变量的等级差数;MSE为均方误差;y为真实值;y'为预测值;N为y的个数。R和ρ越近接近1且MSE的值越小,得出的结果越好。

3 实验及结果分析

3.1 空气质量指数预测

3.1.1 数据准备

本文研究的样本空气数据来源于中国环境监测总站(https://quotsoft.net /air/#archive)发布的南昌市2020年上半年空气质量历史小时数据,共有4369组样本数据,包含影响城市空气质量的六个指标(PM10、PM2.5、NO2、SO2、O3和CO)的浓度以及对应AQI指数。由于得到的数据存在缺失值,因而采用了缺失值上下2个邻近点的平均值对其进行填补。之后对填补完的数据进行平稳性和白噪声检验,结果如表2所示,利用Python的adfuller函数根据计算得到每个指标ADF检验的P1值均小于0.05,可得数据是平稳的;再用acorr_ljungbox函数根据计算得到每个指标白噪声检验的P2值均小于0.05,可得时间序列数据非白噪声,是能预测的。为了减小模型误差,加快模型收敛速度,使用公式(9)做归一化处理,将数据映射到[0,1],当模型的预测结果出来后,再使用公式(10)对预测值进行反归一得到原始值。

3.1.2 各污染物与AQI的相关性分析

本文采用python工具中的相关分析函数得到各指标间的相关性分析热力图,图3所示,得出AQI与各指标都存在一定的相关性,且AQI指数与PM10、PM2.5的相关性最高,可见PM10和PM2.5是污染南昌市空气的“罪魁祸首”。因此,想要有效提升南昌市的空气质量,应着重从降低PM10和PM2.5两种污染物浓度入手。

3.1.3 参数设置及预测

Sigmoid函数的输出范围在[0,1]之间,在训练过程中参数的梯度值为同一符号,更新时就容易出现zigzag现象,很难找到最优值。但tanh函数的取值范围在[-1,1]之间,有效的规避了Sigmoid函数的问题,因此在LSTM层使用tanh函数作为激活函数。linear激活函数具有线性和非饱和的性质,能加快随机梯度下降算法的收敛速度,在Dense层选择了linear函数作为激活函数。随机选择数据集的60%作为训练集,剩余40%一半作为验证集,一半作为测试集。结合时序数据特征,将模型时间步长设置为5,神经元个数为128,dropout比率为0.5,批大小(batch size)为128,样本学习周期为200。为了加快运行速度,在Tensor Flow环境中安装了GPU。

图5 RNN模型预测结果图Fig.5 RNN model prediction result chart

表3 LSTM和RNN模型的评价参数表Tab.3 Evaluation parameter table of LSTM and RNN models

3.2 结果分析

对数据进行分析并设置完模型的参数后,就能将数据带入LSTM空气质量指数预测模型得出预测结果。用改进LSTM模型得出的结果与RNN进行对比,结果如图4、图5所示,LSTM和RNN模型的评价参数见表3。

图4和图5中的虚线为原始数据,实线是测试集预测结果。从表3中可得出LSTM模型的均方误差远优于RNN模型,两种模型的相关系数和斯皮尔曼等级相近,但还是高于RNN模型。综述,LSTM模型的预测结果要优于RNN模型。从图4中可以看出南昌市的空气质量指数(AQI)在[10,100]之间波动,求得平均值约为52。对照表1可知南昌市的空气质量指数(AQI)平均等级为良。

4 结论

空气质量指数受到六个非线性因子的影响,普通的线性回归预测对AQI的分析并不准确,因此本文采用了基于TensorFlow的LSTM神经网络预测模型对AQI做预测。LSTM神经网络能够避免梯度消失或梯度爆炸的问题,具有更好的自我衡量机制,可解决长时依赖问题,对于数据量庞大的非线性多变量时间序列预测有着明显的优势。本文以南昌市的空气质量数据为样本,评估在RNN和LSTM两种神经网络模型下的预测结果。结果显示LSTM模型的均方误差、相关系数和斯皮尔曼等级均优于RNN模型,LSTM对时间序列有更好的预测效果。