一种六维力传感器的信号噪声处理技术

徐明威 张禹 李延斌

摘  要：六维力传感器测量数据时输出信号不可避免地被混合噪声干扰导致降噪性能不佳，同时针对测量噪声/系统噪声模型不准确使得卡尔曼滤波辨识误差大的问题，文章采用了基于Sage-Husa的自适应卡尔曼滤波算法。将六维力传感器采集的数据分别用卡尔曼滤波器/自适应卡尔曼滤波器进行处理，分析了两种算法对传感器测量数据降噪的性能。实验结果表明，基于Sage-Husa的自适应卡尔曼滤波器对测量数据曲线的拟合度与平滑性均优于卡尔曼滤波器，其能够更有效地对随机突变噪声进行降噪处理。

关键词：六维力传感器;系统噪声;测量噪声;自适应卡尔曼滤波

中图分类号：TP241.2        文献标识码：A文章编号：2096-4706（2021）23-0033-04

A Signal Noise Processing Technology of Six-Axis Force Sensor

XU Mingwei， ZHANG Yu， LI Yanbin

（Shenyang University of Technology， Shenyang  110870， China）

Abstract： When the six-axis force sensor measures data， the output signal is inevitably interfered by mixed noise， resulting in poor noise reduction performance. At the same time， aiming at the problem of large identification error of Kalman Filter due to the inaccurate measurement noise / System Noise model， this paper uses Adaptive Kalman Filter algorithm based on Sage-Husa. The data collected by the six-axis force sensor is processed by Kalman Filter/Adaptive Kalman Filter respectively， and the performance of the two algorithms for noise reduction on sensor measurement data is analyzed. Experimental results show that the Adaptive Kalman Filter based on Sage-Husa has better fitting degree and smoothness to the measured data curve than the Kalman Filter， and it can more effectively reduce the noise of random sudden noise.

Keywords： six-axis force sensor; System Noise; measurement noise; Adaptive Kalman Filter

0  引  言

六維力传感器是一种能够实时地检测出空间六个方向力/力矩信息的力传感器，通常被安装在工业机械臂的末端，用来协助工业机械臂进行力/位置控制、孔轴装配、柔顺控制、表面抛光等一些复杂的任务，在工业机械臂的末端安装六维力传感器后，可以实现工业机械臂与外界环境接触时所产生的实时接触力，可以保证人与机械臂交互的安全性并且能以低成本的方式对传统的机械臂进行优化升级[1，2]。

然而，在工程实际应用中六维力传感器由于其敏感元件、设计结构以及放大、采集电路电路带有热噪声并伴随电磁干扰等缘故，其输出信号会不可避免的被混合噪声信号干扰，使得测量的精度变低甚至输出信号不能使用[1]。针对上述问题，本文采用基于Sage-Husa的自适应卡尔曼滤波算法，即先采用经典卡尔曼滤波每次对原始测量信息实施降噪，同时用Sage和Husa提出的一种方法，随着经典卡尔曼滤波迭代更新一次后，噪声协方差Q、系统噪声协方差R也进行一次更新迭代，使得测量噪声/系统噪声参数保持在最优值，降低不确定噪声模型对滤波器的性能影响[2，3]。通过实验的验证与分析，相对于经典卡尔曼滤波算法，基于Sage-Husa的自适应卡尔曼滤波算法相比于经典卡尔曼滤波，对六维力传感器测量数据的降噪效果更加明显，对测量数据曲线拟合也更加的平滑。

1  常见滤波方法

1.1  中值滤波

中值滤波是将一个数据列中的数据个数分为奇数或偶数进行顺序排列，这些数据可以是正序或者倒序的，如若数据列的长度为奇数/偶数时，则数据列的中值就分别为数据列的中间数/中间两数平均值，最终系统的输出信号为该中值[4]。因此，中值滤波算法实现简单，但是，应用范围较小，数据拟合平滑性差并且对突变的噪声信号处理性能不佳。

1.2  加权滑动平均滤波

滑动平均滤波算法是应用最为广泛的滤波算法之一。滑动平均滤波算法是先定义一个缓存区，该缓存区中可容纳N个数据，缓存区中的数据必须为连续采样，且缓存区中的数据个数始终保持不变。当进行采样时，初始采样数据会先占满整个缓存区，当新的采样值进入缓存区后，会将缓存区中最先进入的数据进行剔除，保持该缓存区的长度为N。最终，整个系统的输出为缓存区中数据的算数平均值。而加权滑动平均滤波是在滑动平均滤波的基础上进行期望权重改变，将期望的权重值赋予与不同时刻的数据，一般情况下对当前时刻数据的权重赋予最大值并且权重值向缓存区另一方向逐级递减，可以看出这种算法更看重当前时刻所测量的数据。经过加权滑动平均滤波后得到的结果平滑度高，但是对随机的突变噪声出现时，将最大的权重值赋予带有突变噪声的数据后，会极大地干扰并且降低该滤波器的性能效果，因此加权滑动平困滤波的处理效果不稳定，容易受到随机突变噪声的干扰。

1.3  卡尔曼滤波

卡尔曼滤波算法是卡尔曼提出的一种最优线性状态估计方法。由于实际应用中，测量环境存在着各式各样的混合噪声干扰，卡尔曼滤波算法在这种混合噪声环境下，会对计算结果进行连续的预测计算。卡尔曼滤波的原理就是利用上一时刻的最优预测和此时刻的测量值来进行加权计算，得到当前时刻的最优预测值[5]。根据控制理论，可以给状态变量建立一个状态方程，给测量值建立一个观测方程。

其状态方程为

Xk+1=φkXk+Bkuk+ωk  （1）

其中，Xk+1为k+1时刻n维的系统状态变量，φk为系统状態转移矩阵（增益矩阵）;uk为系统的输入量;Bk为系统输入关系矩阵;ωk为过程噪声。

其观测方程为：

Yk+1=Ck+1Xk+1+γk+1   （2）

其中，Yk+1为k+1时刻的测量值;Ck+1为输出与系统状态的关系矩阵;γk+1为观测噪声。

卡尔曼滤波随着时间更新而不停更新预测值和校正值，其中：

（3）

是利用k时刻的最优估计来预测k+1时刻估计的状态变量，称之为k+1时刻的先验估计值。

（4）

是k+1时刻系统协方差的估计值。

（5）

其中，Kk+1是k+1时刻的卡尔曼增益。

（6）

是k+1时刻利用当前时刻的初始估计值和当前时刻的测量值得到的状态估计，称之为最优估计值。

（7）

Mk+1是k+1时刻的后验状态估计协方差。

其中，式（3）（4）（5）预测方程，（6）（7）为校正方程。

上式（3）（4）（5）（6）（7）即为卡尔曼滤波算法的迭代公式，通过这些迭代公式即可完成卡尔曼滤波算法。

卡尔曼滤波拥有易于实现、迭代效率高、估计精度高等特点，被广泛应用于各种类型的噪声处理、人物识别、自动驾驶等领域[6]。然而，卡尔曼滤波器特别依赖系统噪声和测量噪声模型的准确性。在工程实际应用中，卡尔曼滤波器的测量噪声/系统噪声协方差往往需要通过经验法或者仿真系统确定一个固定的值，故当测量噪声/系统噪声在测量过程中发生随机突变时，卡尔曼滤波器的性难以得到保证。这会导致卡尔曼滤波在迭代过程中容易产生估计误差，导致最终滤波性能降低甚至加重噪声的干扰。

1.4  基于Sage-Husa的自适应卡尔曼滤波

针对以上情况，本文将采用基于Sage-Husa的自适应卡尔曼滤波来解决系统噪声和测量噪声的模型不准确问题，可以实时的更新估计突变噪声的均值/协方差，从而对模型参数和噪声特性进行实时修正，以减少与实际情况的误差，获得更好的估计精度。

基于Sage-Husa的自适应卡尔曼滤波算法是在卡尔曼滤波每次迭代的同时也对噪声模型进行一次更新计算，使得系统噪声和测量噪声均值/协方差的值保持在最优估计值的状态。系统噪声和测量噪声均值/协方差更新如式（8）～（12）所示。

（8）

（9）

（10）

（11）

dk=（1-b）/（1-bk+1） （12）

其中，、分别为系统噪声、测量噪声协方差在k时刻的更新值，dk为加权系数，b为遗忘因子，一般取0.95～0.99。

2  实验结果与分析

2.1  实验流程

本实验采用的实验仪器为安徽埃力智能科技公司所研制的六维力传感器，使用该传感器测量的六维力数据来证明该自适应卡尔曼滤波算法的可行性和降噪性能。该传感器的采样频率为10～5 000 Hz，本实验将频率设置为1 000 Hz即可满足实验要求。

该传感器经过该公司的设计与计算，证明了其在六维方向上是解耦的，故不需要再对传感器进行解耦。并且，在工作的力/力矩量程内，传感器内装置的应力和应变呈线性关系。因此，可以将该算法从一维方向推广到六维方向。实验流程如下所示：将该六维力传感器置于平稳且无外部干扰的环境中，仅对Fz正方向分别施加0 N、30 N的力，即此时Fx=0 N，Fy=0 N，Mx=0 N，My=0 N，Mz=0 N，Fz=0或30 N。

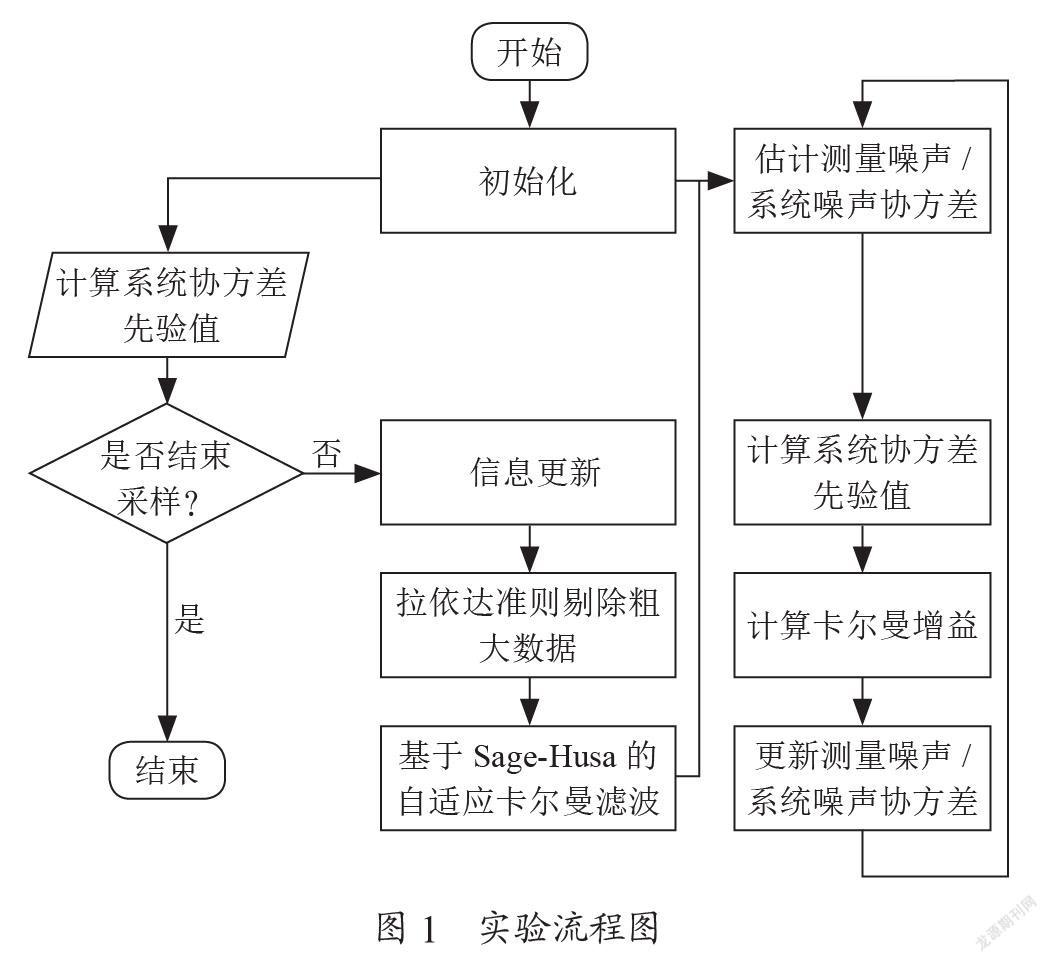
由于卡尔曼滤波在初始阶段进行迭代优化导致精确度不高[7，8]，故该实验将0～30 s定义为初始阶段，此阶段不采集/处理数据，从30 s开始采集数据到60 s停止采集数据，共计采集数据时间为30 s。当度过初始阶段时开始采集数据时，将采集的数据分别使用卡尔曼滤波/自适应卡尔曼滤波算法进行滤波降噪。根据工程实践的经验法，将采集系统中卡尔曼滤波器的系统噪声协方差Q设为0.102 1，测量噪声协方差R设为0.251 1。实验流程图如图1所示。

2.2  上位机采集系统

本文中使用的六维力传感器上位机采集系统是基于vc6.0中的微软基础类库（MFC）所编写的，MFC编程具有便捷的程序编写以及提供操作界面，能够对传感器的数据进行实时采集、算法处理、数据显示以及储存等功能[9，10]。将上述算法编写进程序后，准备实验。软件界面设计如图2所示。

2.3  实验结果与分析

首先令Fz=0 N。使用卡尔曼滤波对采集到的六维力传感器Z轴整方向上力数据进行滤波降噪。其结果如图3所示。

分析图3可以得出，当卡尔曼滤波度过初始阶段后，卡尔曼滤波处理传感器的随机突变噪声有一定的作用。但是，在实际应用中，卡尔曼滤波的测量噪声/系统噪声协方差在大多数情况下为经验法固定的值，不能灵活的应对突变的噪声信号，导致滤波信号波动性较大，平滑度不理想。

再使用自适应卡尔曼滤波进行滤波然后与卡尔曼滤波进行比较分析。其结果如图4、图5所示。

分析图4、图5可以发现，当自适应卡尔曼滤波度过初始阶段，在对数据进行滤波处理后的结果与卡尔曼滤波类似，依然有一定的误差。但是，相比于卡尔曼滤波，自适应卡尔曼滤波在处理数据的过程中不断地自我更新测量噪声/系统噪声协方差，能够更加灵活地处理极端噪声，其平滑曲线与测量数据有更好的拟合度，曲线更为平滑，对六维力传感器的降噪效果更好。

再對该滤波算法的普适性进行验证。在六维力传感器的Z轴正方向上施加一个恒为30 N的力，令Fz=30 N。使用卡尔曼滤波对采集到的六维力传感器Z方向上数据进行卡尔曼滤波/自适应卡尔曼滤波降噪处理。其结果如图6、图7所示。

通过对图6、图7的分析，可以看出当Fz=30 N时，经过自适应卡尔曼滤波对数据进行滤波处理后的结果与Fz=0 N时结果相同，自适应卡尔曼滤波与卡尔曼滤波相比有更灵活的降噪性能与平滑性，对六维力传感器的降噪效果更好，同时也验证了自适应卡尔曼滤波的有效性和可行性。

3  结  论

卡尔曼滤波器是当前应用最广泛的线性最优滤波器。但是，在工程实践应用中卡尔曼滤波器的测量噪声/系统噪声协方差往往都根据经验法分别设定一个定值，故当测量噪声/系统噪声在测量过程中由于混合噪声发生随机突变时，卡尔曼滤波器的性能容易受到噪声模型不准确导致降噪性能不佳。为解决这一问题，采用基于Sage-Husa提出的自适应卡尔曼滤波，在卡尔曼滤波每次进行迭代时也对噪声协方差Q、系统噪声协方差R进行一次更新迭代，保证系统/测量噪声模型参数实时的保持在最优值，从而降低不确定噪声模型对卡尔曼滤波器的性能影响。基于上述实验的验证与分析表明，基于Sage-Husa的自适应卡尔曼滤波相比于卡尔曼滤波器既能更加有效地对六维力传感器测量的力数据进行降噪，同时也与测量数据有良好的拟合度、平滑性，能够有效降低测量噪声协方差Q与系统噪声协方差R的变化对测量精度带来的影响。

参考文献：

[1] CHEN F，ZHAO H，LI D W，et al. Contact force control and vibration suppression in robotic polishing with a smart end effector [J].Robotics and Computer-Integrate-d Manufacturing，2019，57：391 -403.

[2] 张立建，胡瑞卿，易旺民.基于六维力传感器的工业机器人末端负载受力感知研究 [J].自动化学报，2017，43（3）：439-447.

[3] 汪志红.电阻应变片式六维力传感器弹性体力学特性的研究 [D].芜湖：安徽工程大学，2013.

[4] 宋会杰，董绍武，屈俐俐，等.基于Sage窗的自适应Kalman滤波用于钟差预报研究 [J].仪器仪表学报，2017，38（7）：1809-1816.

[5] 邵腾.面向参数不精准系统的Kalman滤波理论研究 [D].杭州：杭州电子科技大学，2016.

[6] 靳松，朱兆林，张旺，等.基于LabVIEW的中值滤波算法在剔除尖脉冲干扰中的应用 [J].机电产品开发与创新，2021，34（5）：22-24.

[7] 黄小平.卡尔曼滤波原理及应用 [M].北京：电子工业出版社，2015：32-35.

[8] WANG H R，DENG Z H，FENG B，et al.An adaptive Kalman filter estimating process noise covariance [J].Neurocomputing，2017，233（5）：12-17.

[9] 乔尚岭.无耦合六维力—力矩传感器数据采集系统研究 [D].哈尔滨：哈尔滨工业大学，2014.

[10] 罗家浒，杨会成，曹会彬，等.六维力传感器静态条件下的信号噪声处理 [J].计算机仿真，2018，35（1）：378-381.

作者简介：徐明威（1996.07—），男，汉族，福建漳平人，硕士研究生，研究方向：遥操作机器人和六维力传感器技术。