基于ANSYS模拟的引水渡槽水利工程动力响应特征分析研究

邱德俊，仲静文，周 洋

(南京市水利规划设计院股份有限公司，南京 210000)

1 概 述

水资源作为人类生存发展的基础，最大程度高效利用水资源是许多水利工程师一生致力于研究的问题[1-3]。作为许多缺水地区，引水、提水、蓄水等水利工程为枯水期水资源缺乏提供备用资源，建设这些水利工程不可忽视其安全稳定性[4-6]。作为水利工程安全稳定性评价的重要一方面，结构动力响应特征在许多工程应用研究较广泛。一些学者通过水工模型试验，研究室内试验下水工模型的振动破坏特征，为工程设计施工提供重要参考[7-10]。同时在工程现场安装监测传感器，并研究相关数据之间的联系性，及时预判水利工程失稳破坏临界点[11-12]。有限元数值方法作为一种高效的计算手段，近年来应用在各类复杂工程场景下，本文针对工程动力响应问题，引入有限元进行模拟求解，并分析结构动力响应特征[13-15]，为评估工程安全稳定性提供重要理论参考。

2 结构动力响应理论

与静力荷载分析不同，动力荷载作用下结构各节点应力与位移分布实质上处于在某一频率影响范围内，当不同振动频率下应力变形场分布与量值均会出现较大差异，因而针对动力荷载下结构动力响应特征应采用模态分析手段，通过模态分析获得不同阶次下的频率以及振型特征，而各阶次下振动方程均服从以下表达式[16]：

[M]{x}+[C]{u}+[K]{v}=0

(1)

式中：[M]为质量无量纲数值矩阵；[C]为阻尼无量纲数值矩阵；[K]为刚度无量纲数值矩阵；{x}为位移运动特征参数矩阵式；{u}为速度运动特征参数矩阵式；{v}为加速度运动特征参数矩阵式。

在不考虑其他静荷载下的阻尼影响，其振动方程可转变为：

[M]+tω[C]-ω2[M]{x}=0

(2)

式中：ω为角速度，rad/s；t为振动时间，s。

上述振动运动方程实质上仅为结构在固体求解域内的表达，当处于多相场条件下，其由于流场或其他场影响，结构运动方程会受到一定改变，各位移等运动特征参数均会发生改变，此时需要考虑多场耦合下的结构运动特征参数。故而，针对流固耦合场，引入系统质量与动量守恒定律，有[17]：

(3)

式中：ff为流体速度矢量，m/s；τf为剪应力矢量，Pa；v为固体速度矢量，m/s；t为振动时间，s；ρf为流体密度参数，g/cm3。

式(3)中剪应力矢量可表述为：

τf=(-p+μ∇·v)I+2μe

(4)

式中：μ为动力黏度系数，无量纲；e为应力张量，N；p为压力参数，无量纲；I为应力张量第一不变量，无量纲。

另外固体域内节点又服从牛顿运动方程，有：

ρsvs=∇·σs+Fs

(5)

式中：vs为加速度矢量，m/s2；σs、Fs均为不同矢量力，N；ρs为固体密度参数，g/cm3。

综合固体域与流场影响，以能量传递作为中间联系量，获得能量方程表达式为：

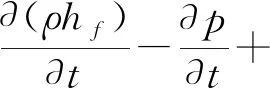
(6)

式中：λ为传热系数，无量纲；SE为能量常数项，无量纲；ρ为固体场密度，g/cm3；hf为流体总焓，kJ；T为温度，K；τ为剪切力，N；∇为梯度算子；其他参数同上。

根据地震动荷载下，需将地震动荷载参数转变至系统能量体系中，而每个作用节点上地震动荷载可表示为：

(7)

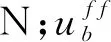
根据材料力学理论值，节点发生应力应变实质上是能量的传递变化，故而可知地震动荷载作用下，其能量表现参数可用位移等运动特征参数表现。根据上式获得地震动荷载作用下，其中某个时间节点处的运动特征参数为：

(8)

(9)

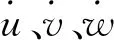
3 工程概况

苏北地区水资源人均占有量较低，对当地经济社会发展均有较大影响，特别是在枯水期水资源人均占有量平均下降18%，且地区个别城市出现生活缺水。为提升该地区水资源供应量，设计有引黄工程，在吕梁西部地区建设有一渡槽水利设施，通过枯水期集水1 070 km2，设计峰值流量为4 000 m3/s，建设有长度约80 km的输水干渠，通往各个提水工程点，渠首流量设计为0.7 m3/s，可满足短水地区农业生产用水及生活用水。该渡槽包括有进出口水闸、防渗结构及槽基础等，其中槽基础采用筏板基础，设置有弧形钢闸门，其启闭开度均以液压式程序控制，保证过流的流量精确度。槽身挡水结构长度约为600 m，防渗结构设置有厚度40 cm的混凝土抹面墙，墙面并铺设有土工止水布。结构顶部高程约为120.3 m，设计水深为6.5 m，以多孔槽位通流断面，每个槽断面宽度为6.5 m，高度为7.5 m，支撑荷载的槽墩结构净距为28 m。设计的多扇渡槽孔示意图见图1。

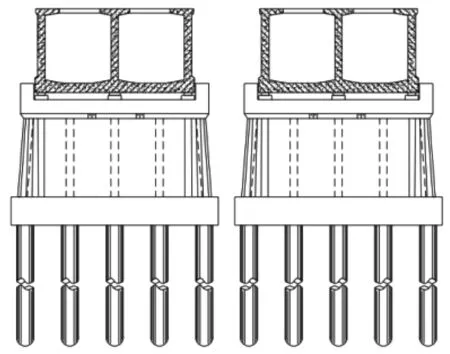
图1 多扇渡槽孔示意图

根据工程设计资料得知，该渡槽水工结构包括有上盖层、中部承台与下部墩身。上盖层宽度为5.5 m；承台高度设计为3 m，在多扇槽横向上有22 m，顺水流方向设计为7.8 m；下部墩身最大高度为17.5 m，厚度约为1 m，各个墩身之间以厚度为80 cm的砌体墙分隔开，各结构部位均以钢筋混凝土材料制作。工程现场资料显示，基岩层为弱风化灰岩，钻孔取出样品表明，灰岩颗粒粒径较大，完整性较好，表面无可见显著孔隙，承载强度较高，适合作为渡槽水利设施的支撑结构。另在表面覆盖层分布有第四系杂填土，厚度差异较大，最厚处为4.5 m，松散程度较高，透水性较强；在基岩层上还分布有一层砂砾土，夹有粒径1.6～6.8 mm的碎石，可作为渡槽连接的输水渠道渠基础持力层，防渗性较佳。结构整体刚度较大，流固耦合场下外荷载包括有槽身与支撑结构自重，以及渡槽内水流荷载。

4 渡槽结构动力响应分析

4.1 模型建立与研究工况

根据前述工程资料分析基础下，利用ANSYS有限元软件建立渡槽三维模型，见图2。以SOLID65模型作为网格单元体，具有8个方向变形自由度，适用于动力荷载下求解，划分网格单元数80 864个，节点数58 668个。以顺渡槽的横纵向为X、Z向，竖向沉降方向为Y负向。研究工况分为渡槽内有、无水两种工况开展研究，其中有水工况设定水深6.5 m。

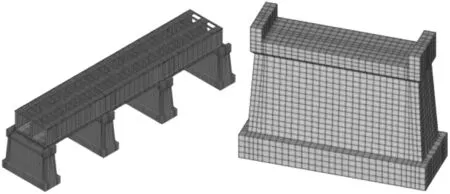
图2 渡槽三维有限元模型

4.2 自振特性分析

通过ANSYS有限元软件获得有、无水工况下的振型云图，见图3。从无水工况下渡槽结构整体振型特征可看出，无论是在第1阶次亦或是第10阶次，渡槽结构振型特征均呈现以渡槽横向方向为轴线对称式分布。从各阶次振型来看，第1阶振型以纵向运动为主，振型倾向于纵向变形；第3阶次振型特征具有弯扭复合变形特征，即以水平向与竖向叠加变形；当计算阶次增大至10阶时，渡槽结构不仅是弯扭复合状态，而且还包括有纵向平移运动特征，不仅受弯、扭也有拉伸与压缩变形。分析表明，随着计算阶次增大，渡槽结构不仅在纵向方向上刚度受到威胁，而且会成为组合变形状态，多方向同时受到不同形态变形，即渡槽设计时首先应在纵向方向补充刚度。

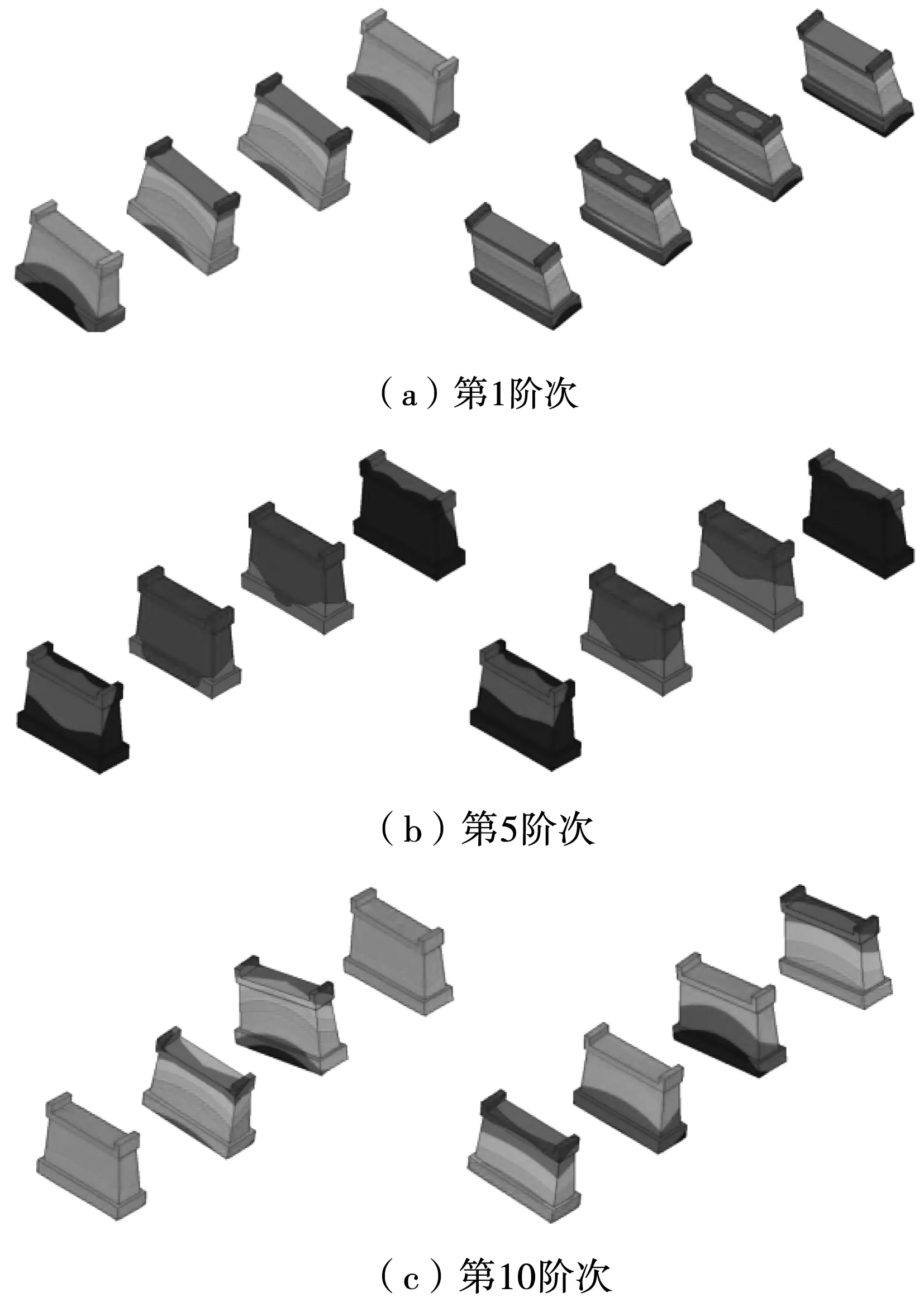
图3 渡槽结构自振振型云图(左右分别为无水、有水工况)

对比无水工况振型特征，有水工况下振型分布更趋于提前进入多组合变形振型。在第10阶次时，其每个槽墩均受到比无水工况下组合变形体更强的振型运动，但两个工况下亦有类似之处的振型分布：均以渡槽横向方向为轴线，振型对称分布。分析表明，水流自重压力对振型分布特征影响较弱，仅对渡槽结构墩身振型分布强度有所提高。另一方面，有、无水工况下在低阶次振型分别以纵向、横向运动作为起始分布，因而渡槽结构的支撑载体应重点对横、纵向刚度起到稳定作用。

图4为有、无水工况下渡槽结构自振频率与计算阶次关系曲线。从图4中可看出，两个工况下结构自振频率均与计算阶次呈正相关，第1阶次下自振频率为2.41，无水工况下第10阶次相比第1阶次增大2.3倍，而有水工况下同类对比幅度约为2.86倍；而无水工况下第20阶次相比第10阶次增大48.3%，有水工况相同阶次的对比增幅约为40.1%。分析表明，虽然各阶次下自振频率均随计算阶次递增，但增长幅度会有一定差异，两个工况下均呈现前10阶次自振频率增长幅度高于后10阶次。对比两个工况同计算阶次下自振频率可知，有水工况下自振频率显著低于无水工况，第1阶次下有水工况相比无水工况降低26.2%，第10阶次、20阶次下降低幅度分别为13.5%和10.1%，即有水工况下受水流作用力影响，自振频率会出现一定程度降低，因而渡槽进行动力设计时，应充分考虑流固耦合之间作用力，满足水流对结构自振频率影响要求。

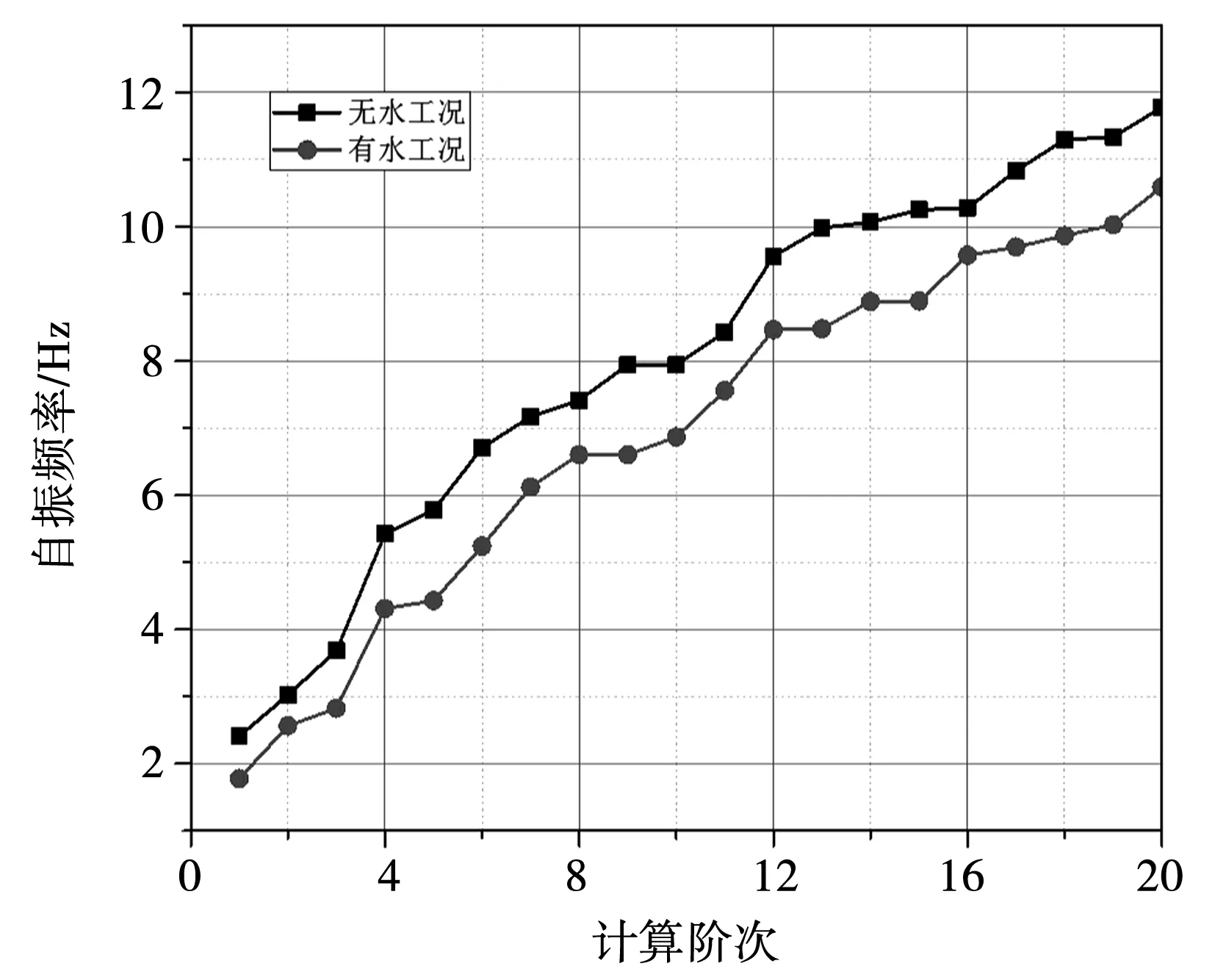
图4 自振频率与计算阶次关系曲线

4.3 地震动响应特征

针对地震荷载下渡槽结构动力响应特征，本文以人工合成地震波作为地震荷载施加依据，其加速度谱见图5。流固耦合作用力以附加质量模型进行模拟计算，各正方向标定与前文一致。为分析方便，以渡槽支撑结构中4个特征点(上部顶盖层点A、盖层与墩身接触区域点B、承台与墩身交界点C、下部承台点D)开展应力与加速度特征分析。

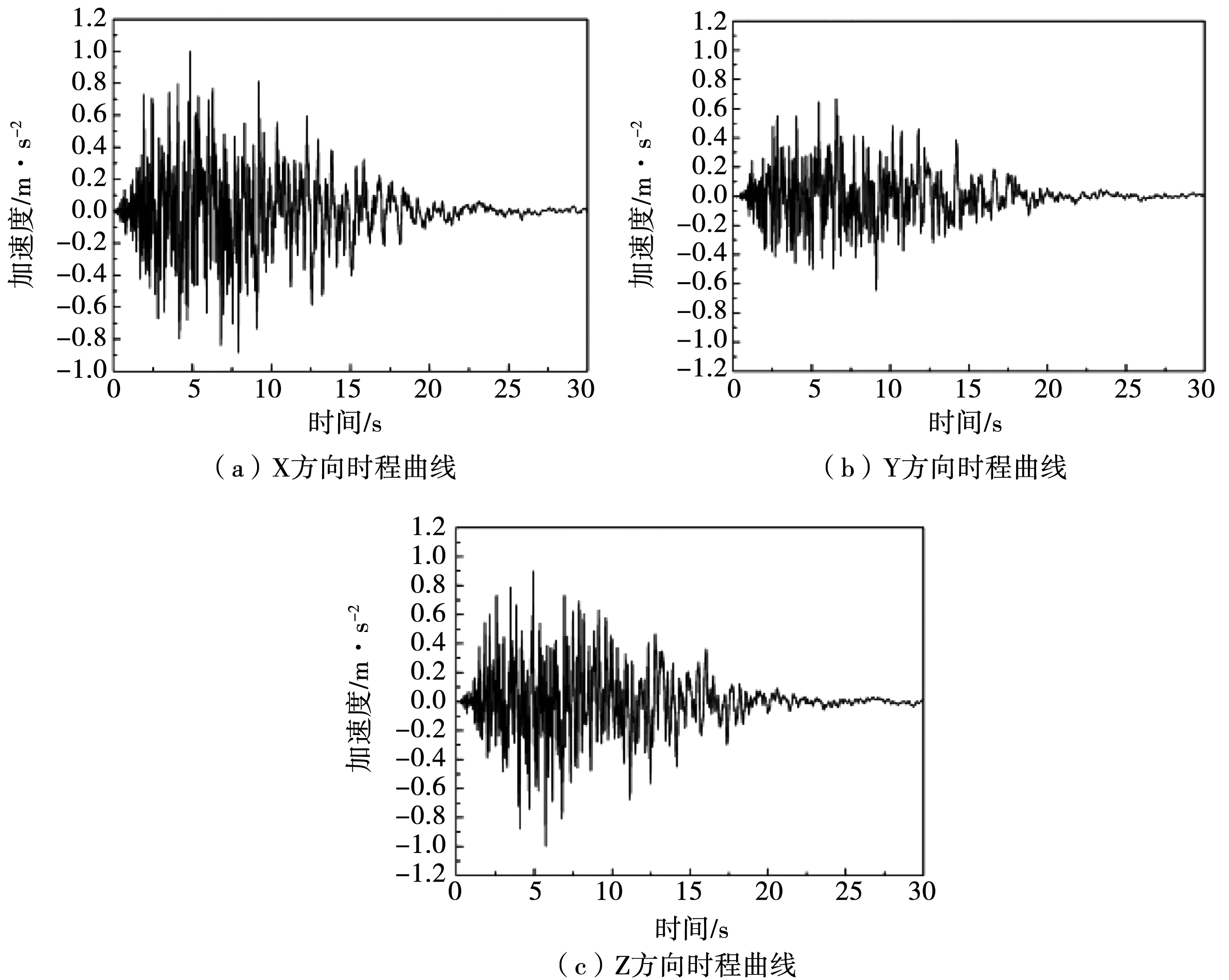
图5 地震荷载时程曲线

图6 渡槽支撑结构应力分布云图

图6为计算获得地震动荷载下渡槽支撑结构各特征点第一主应力分布云图。从图6中可看出，4个槽墩应力分布基本类似，最大主应力为2.01 MPa，出现在槽墩边角边缘侧；对比4个特征点应力值可知，点A第一主应力约为0.352 MPa，点B第一主应力相比增长67.1%，点C、点D相比前两个点均有大幅度增加，其中下部承台点D第一主应力1.77 MPa，即4个特征点中以承台上应力为最大。动力设计时，若有必要应对承台设置加固结构，增强承台受力稳定性。

基于ANSYS计算获得地震荷载下渡槽结构上4个特征点加速度特征(图7)，分别为顺渡槽向与竖向的加速度时程曲线。从图7中可看出，4个特征点同一方向上加速度时程曲线走向基本类似，且特征点峰值加速度基本一致，顺渡槽向峰值加速度均维持在0.35 m/s2。对比两个方向的峰值加速度可发现，竖向加速度峰值相比顺渡槽横向要低，4个特征点渡槽竖向峰值加速度约为0.17 m/s2，相比顺渡槽向降低51.4%，即表明地震荷载作用主要针对渡槽水平向，竖向方向地震荷载作用影响较弱。

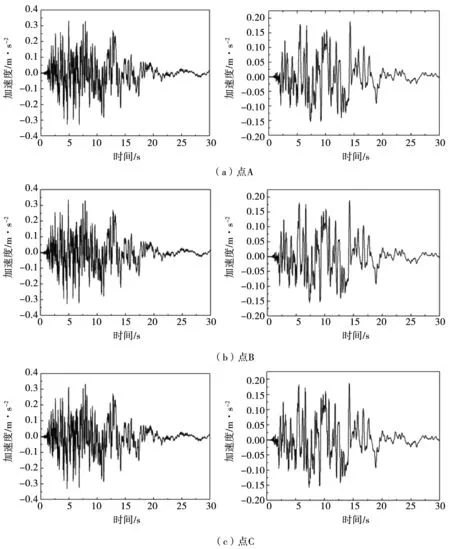
图7 4个特征点加速度时程曲线

5 结 论

针对苏北某引水渡槽水利工程开展地震动力响应特征分析，利用ANSYS有限元软件建立三维有限元模型，分析了渡槽结构自振特性与地震动力响应特征，结论如下：

1) 研究获得了渡槽结构在各阶次中振型均以渡槽横向方向为轴线对称式分布，低阶次下均以纵向运动分布为主，高阶次下具有多组合变形振型，水流作用下振型分布影响较低，仅改变了振型分布强度。

2) 研究了有、无水工况下自振频率与计算阶次关系，结构自振频率均与计算阶次呈正相关，但前10阶次自振频率增长幅度高于后10阶次，有水工况下自振频率显著低于无水工况，无水工况下第10阶次相比第1阶次增大2.3倍，第20阶次相比第10阶次增大48.3%，第1阶次下有水工况相比无水工况降低26.2%。

3) 获得了渡槽支撑结构各特征点第一主应力分布，4个特征点中以承台上应力为最大，达1.77 MPa；4个特征点同一方向加速度时程曲线走向基本类似，特征点峰值加速度基本一致，顺渡槽向峰值加速度均维持在0.35 m/s2，竖向加速度峰值相比顺渡槽横向降低51.4%，达0.17 m/s2。