河道防洪枢纽控制工程中栅墩纵梁参数对结构动力影响特征研究

俞 荣，刘泽人，夏友超

(1.南京振高建设有限公司，南京 211300； 2.南京市水利规划设计院股份有限公司，南京 210001； 3.苏交科集团股份有限公司，南京 210003)

1 概 述

水利工程中抗震设计也较为重要，水工建筑结构只有具备良好的抗震性能，才能更好地长期安全稳定运营，因而许多水利工程师借助各种手段来提升水工结构的动力抗震性能，在一定程度上也提升了水利工程的设计水平[1-2]。原型物理实验在水利工程中运用较广，它采用原型尺寸设计水工建筑，并借助振动台等室内大型试验仪器，研究结构破坏过程中动力响应特征，为结构设计提供具体试验参数[3-5]。采用微震等现场监测仪器或原位测试仪器对工程现场水工建筑开展监测测试，能够获取到水利工程运营过程中的数据特征变化，为工程师预判水利安全状态提供重要参考[6-8]。仿真计算能够较好模拟不同运营工况下水利建筑所处环境，并结合不同设计方案，分析各设计方案下水工建筑的动力或静力特征，从而为水工设计提供计算参数或模拟运营[9-11]。本文利用ANSYS仿真手段，计算获得不同设计方案下栅墩动力响应特征，为确定最佳抗震设计方案提供重要计算依据。

2 工程资料

2.1 工程概况

某河道防洪枢纽工程包括上游拦污栅墩、节制闸、输水隧洞及大坝堤防工程，为下游通航以及生产生活提供安全保障。枯水期甚至可以保证地区缺水率不会超过4%，同时可承担地区超过1 000 km2面积农田，提升了区域水资源利用效率与水利工程安全性。拦污栅墩作为该水利枢纽工程重要水工结构设施，其迎水侧是正常蓄水位高程379 m的大型水库，总库容设计为6 000×104m3，大坝堤防高程423.5 m，拦污栅墩设置于堤防大坝K+125 m处，具有过滤泥沙、减弱泥沙对水闸及堤防工程的流体冲刷作用。拦污栅墩后连接输水渠道，渠首流量为0.65 m3/s，干渠总长度约125 km，以模袋式混凝土作为衬砌形式，保证输水渠道安全稳定性。整个堤防工程中设计进水孔2个，分布于拦污栅墩下游，每个出水口为3.5 m×6.8 m，采用弧型钢闸门作为水流量调控设施，设计有电脑程序精确控制式的液压启闭机，保证通行水流安全性与输水效率。拦污栅设置有6根支撑墩，栅墩之间的间距为4 m，均采用预应力混凝土浇筑形成。设置有预应力锚索与锚固洞连接，保证闸墩安全可靠性。锚索共有4根主锚索与3根次锚索，主锚索横贯在纵向梁上，上下排主锚索间距为1.4 m，次锚索靠近闸墩承载平台边缘设置，中间次锚索距离闸墩顶部2.2 m，锚索布设剖面形态见图1。

图1 锚索结构平面布置图

目前由于该防洪枢纽工程运行时间较久，部分水工结构出现老化及渗漏，极大地威胁了整体水利结构安全稳定性。特别是在闸墩纵向梁上，作为拦污栅墩在纵向剖面上的承载结构，其安全可靠性对工程运营具有重大意义，因而对栅墩纵向梁安全加固设计很有必要。布设在栅墩纵向方向的纵向梁，轴向长度为1.5 m，目前工程设计部门考虑对该栅墩纵向梁的截面体型开展设计方案对比研究，以此获取最适合该栅墩纵向梁截面的最佳方案。

针对纵向梁截面体型设计方案，考虑采用数值仿真计算手段，针对性解决不同纵向梁截面设计方案下栅墩整体应力变形特征，因而数值计算首先需解决目前堤防枢纽工程场地地质状态，获取相关岩土物理力学参数，确保各方案计算准确性。根据现场原位测试资料得知，该枢纽工程位于弱风化花岗岩层上，该基岩稳定性较好。现场所取出样芯表明花岗岩完整性较好，表面无显著孔隙，室内测试单轴抗压强度接近60 MPa，三向压力测试气体渗透率最低仅为10-18m2。表面覆盖土层为第四系堆积土层，松散性较大，局部变形程度较高，承载力较低，输水渠道持力层甚至都穿过该层，位于下卧砂土层中，砂土粒径最大仅为4 mm，含水量较低，承载力中等，渠道采用厚20 cm碎石垫层铺设在此层上，即可满足承载力要求。在上述工程资料及参数测试结果下，以地震动荷载作为约束，所采用地震动荷载实质上为EI Centro地震波，设计反应谱法叠加动力荷载，根据不同栅墩纵梁截面体型设计方案，分别计算获得栅墩结构动力响应特征，为评判最优方案提供计算依据。

2.2 模型建立及动荷载

借助ANSYS软件，按照栅墩整体几何形态建立数值模型，且以六面变形体为基本单元体，经划分模型网格单元后共获得单元总数198 738个，节点数96 538个，所建立栅墩仿真模型见图2。有限元模型中，空间坐标体系X、Y、Z正方向分别为水流右侧垂线方向、顺水流向、向上竖向。对比纵梁不同截面体型，只需改变纵梁剖面不同几何设计参数，即可对比各方案下动力响应特征。

图2 有限元仿真模型

边界约束荷载考虑栅墩结构自重，外荷载为地震动作用，以拟静力法考虑将地震动作用分为惯性力与动水压力影响。其中惯性力以反应谱作为荷载确认，本文地震动反应谱以EI Centro地震波作为施加荷载，其反应谱见图3，按照空间体系中3个方向，分别作用在结构模型网格单元节点上。由于堤防工程迎水侧正常蓄水，因而所考虑的动水压力M′根据式(1)计算[12-14]，按照力作用点施加在栅墩地基结构体系中。

(1)

式中：H为深度；Zi、Ai分别为坝基距离与截面积；ρw为流体密度。

图3 加速度反应谱实测值

3 纵梁截面体型设计参数对动力特性的影响特征

3.1 纵梁截面高度

为研究纵梁截面高度参数对栅墩动力特性影响，在设计纵梁截面宽度均为0.5 m情况下，设定各截面高度分别为0.5 m(A方案)、1 m(B方案)、1.5 m(C方案)、2 m(D方案)4个方案，各截面体型方案见图4。

图4 不同截面高度设计方案(宽度均为0.5 m)

3.1.1 应力特征

经仿真计算获得纵梁不同截面高度下应力变化特征，见图5。从图5中可看出，纵梁上最大拉应力与截面高度参数为正相关关系，当截面高度为0.5 m时，纵梁上最大拉应力为7.1 MPa；而当截面高度增大至1.5和2 m后，纵梁最大拉应力相比前者分别增大14.3%和17.1%。分析认为当纵梁截面高度增大后，栅墩横梁上会过渡影响至纵梁，造成纵梁上拉应力有所增大。相比纵梁上最大拉应力递增态势，栅墩承台上最大拉应力与截面高度并无显著关联性，承台最大拉应力随截面高度增大而稳定不变，最大拉应力均维持在9 MPa左右。腰墙上最大拉应力相比纵梁、承台最大拉应力均要低很多，当截面高度均为1 m时，腰墙上最大拉应力为2 MPa，仅为同设计方案下纵梁、承台最大拉应力的27.7%和22.7%；当截面高度增大时，腰墙上最大拉应力在截面高度1 m后增长显著，截面高度2 m时最大拉应力相比高度1 m时增大21%。从工程安全性角度考虑，当截面高度在1m以下时，更有利于腰墙结构安全稳定性。

图5 不同截面高度下最大拉应力变化特征

3.1.2 变形特征

图6为不同截面高度设计参数下栅墩各方向位移变化值。从图6中可知，栅墩X、Y向位移在截面高度递增过程中几乎无较大变化，分别稳定在14和13.7 mm，即截面高度改变并不影响栅墩在X、Y向上所发生的动力位移响应。栅墩Z向位移随截面高度增大逐渐减小，高度0.5 m时栅墩Z向位移值为4.4 mm；而截面高度为1.5和2 m时的位移值相比前者分别降低6.8%和9.1%，表明截面高度设计参数愈大，可稍微抑制栅墩Z向位移发展。

图6 不同截面高度下位移变化特征

3.2 纵梁截面宽度

针对纵梁截面体型宽度设计，设定各方案截面高度均为2 m，截面宽度分别为0.5 m(1#方案)、1 m(2#方案)、1.5 m(3#方案)、2 m(4#方案)，4个截面体型方案剖面形态见图7。

图7 不同截面宽度设计方案(高度均为2 m)

3.2.1 应力特征

图8为纵梁截面宽度影响下各特征部位最大拉应力变化特征。从图8中可看出，纵梁最大拉应力在宽度设计参数增大情况下有所递增，但幅度较小。截面宽度为0.5 m时，最大拉应力为8.3 MPa；而宽度增大至1.5和2 m后，最大拉应力增长幅度分别仅为11.8%和12.1%。腰墙最大拉应力随截面宽度变化特征与纵梁相类似，其最大拉应力在截面宽度超过1.5 m后增长处于停滞。与纵梁、腰墙有所差异的是栅墩承台，其最大拉应力随截面宽度设计参数递减。在宽度为0.5 m时的栅墩承台最大拉应力为9 MPa；而宽度增大至1.5和2 m后，最大拉应力相比前者分别降低6.6%和9.8%。由此表明，截面设计宽度参数增大会抑制其最大拉应力的发展态势，即纵梁截面宽度设计参数在1.5 m以下具有较好抑制闸墩张拉破坏。

图8 不同截面宽度下最大拉应力变化特征

3.2.2 变形特征

经仿真计算各设计方案下纵梁变形状态，获得闸墩各方向位移值随纵梁截面宽度参数变化曲线，见图9。从整体来看，栅墩X、Y、Z向位移随截面宽度设计参数几乎无较大变化，且X向位移与Y向位移基本接近一致，两者位移值均在14 mm左右；Z向位移相比X、Y向位移均较小，在截面宽度1 m时，Z向位移仅为X向位移的28.6%。分析认为，截面宽度设计参数过大或过小，并不影响栅墩各向位移的稳定。

图9 不同截面宽度下位移变化特征

4 纵梁截面体型综合设计方案分析

前文均是在纵梁截面单一设计参数变量条件下研究闸墩应力变形变化特征，而针对综合尺寸影响特性研究较少。本文基于纵梁截面体型高度设计参数不低于宽度这一准则，共设计出10个研究方案，即高、宽分别设计为2 m×2 m(a方案)、2 m×1.5 m(b方案)、2 m×1 m(c方案)、2 m×0.5 m(d方案)、1.5 m×1.5 m(e方案)、1.5 m×1 m(f方案)、1.5 m×0.5 m(g方案)、1 m×1 m(h方案)、1 m×0.5 m(i方案)、0.5 m×0.5 m(j方案)，典型设计方案截面体型见图10。

图10 典型设计方案截面体型示意图

4.1 综合设计方案应力变形特征

图11为计算获得各设计方案下最大拉应力、栅墩位移变化特征。从图11(a)可看出，纵梁截面体型所占面积愈大，则纵梁拉应力愈大，a、b两方案纵梁拉应力最大可达9.2 MPa，e方案纵梁拉应力达9 MPa，当截面体型设计参数为j方案时，其最大拉应力相比a方案降低23.9%，即截面体型面积不应过大，应保持在0.25 m2以下。栅墩承台最大拉应力基本随截面积增大而递减，在截面高、宽均为2 m时，栅墩承台最大拉应力为9.1 MPa，而截面高、宽分别为i、j方案后，其最大拉应力相比a方案分别降低17.6%和19.8%。腰墙最大拉应力最大不超过3.1 MPa，但当截面高、宽均低于1.5 m后，腰墙最大拉应力均低于3 MPa，i、j方案腰墙最大拉应力分别为2和2.2 MPa。

另一方面从栅墩各向位移特征来看，X向位移基本随截面体型变化稳定在14 mm左右；Y向位移亦是如此，长期稳定在13.8 mm左右；Z向位移相比X、Y向位移均较小，其在各设计方案中整体稍有增大，但增幅较小。j方案位移值为4.41 mm，相比a方案Z向位移增大14%。

4.2 综合设计方案比选

综合各设计方案及截面高度、宽度影响因素，本文认为截面高度、宽度均为0.5 m时，不论是动力响应下的最大拉应力亦或是位移特征，均处于较安全状态，图12、图13即为该方案下各特征部位应力分布、位移响应特征。由应力分布云图可看出，闸墩横纵梁上最大拉应力分布区域并不较多，最大拉应力所处区域并不影响闸墩横纵梁整体安全抗震设计；而腰墙上最大拉应力仅为2.3 MPa，分布在墙边缘侧，分布范围亦较小。栅墩各向动力响应位移亦较小，特别是Z向沉降位移无显著聚集性分布带，因而选择j方案最为合理。

图11 综合因素设计方案下动力响应特征

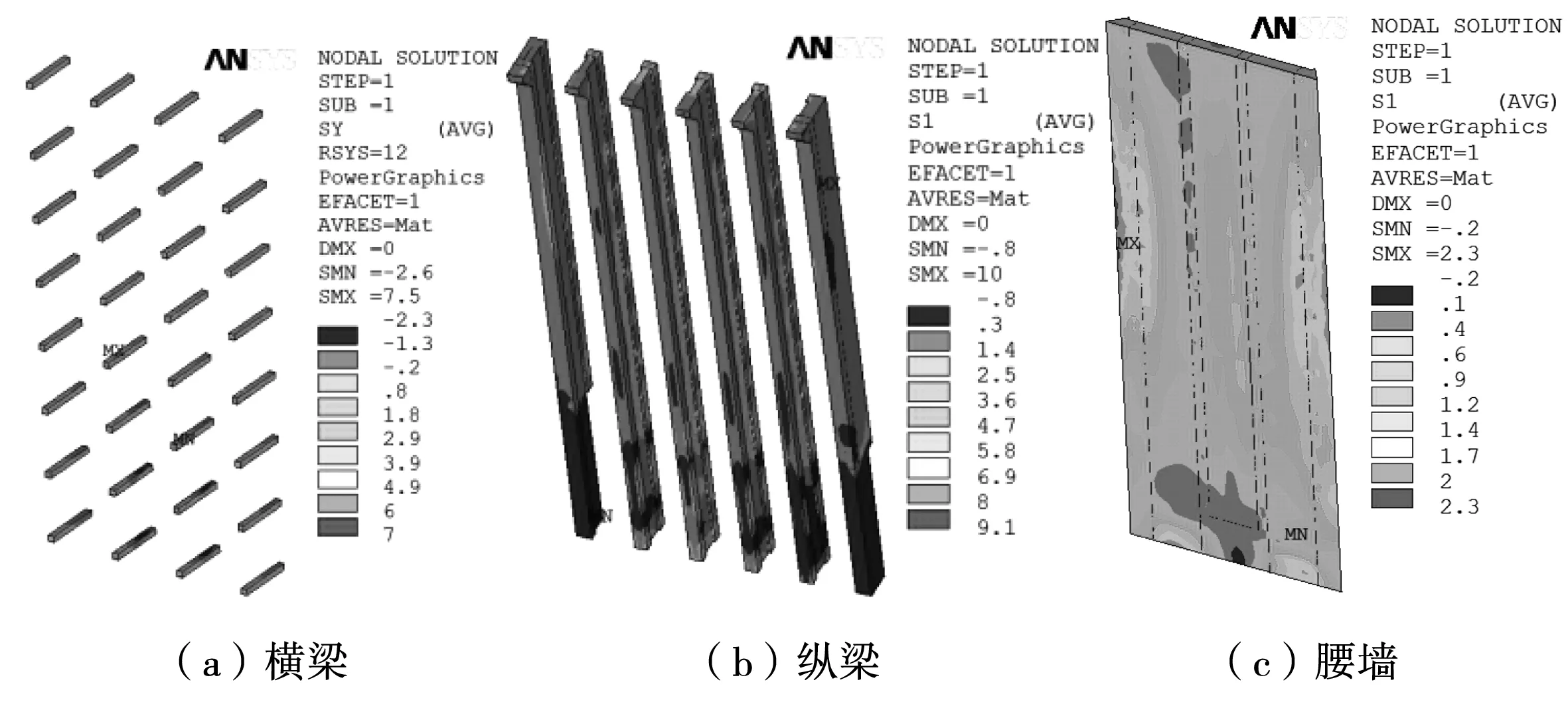
图12 各特征部位应力分布特征

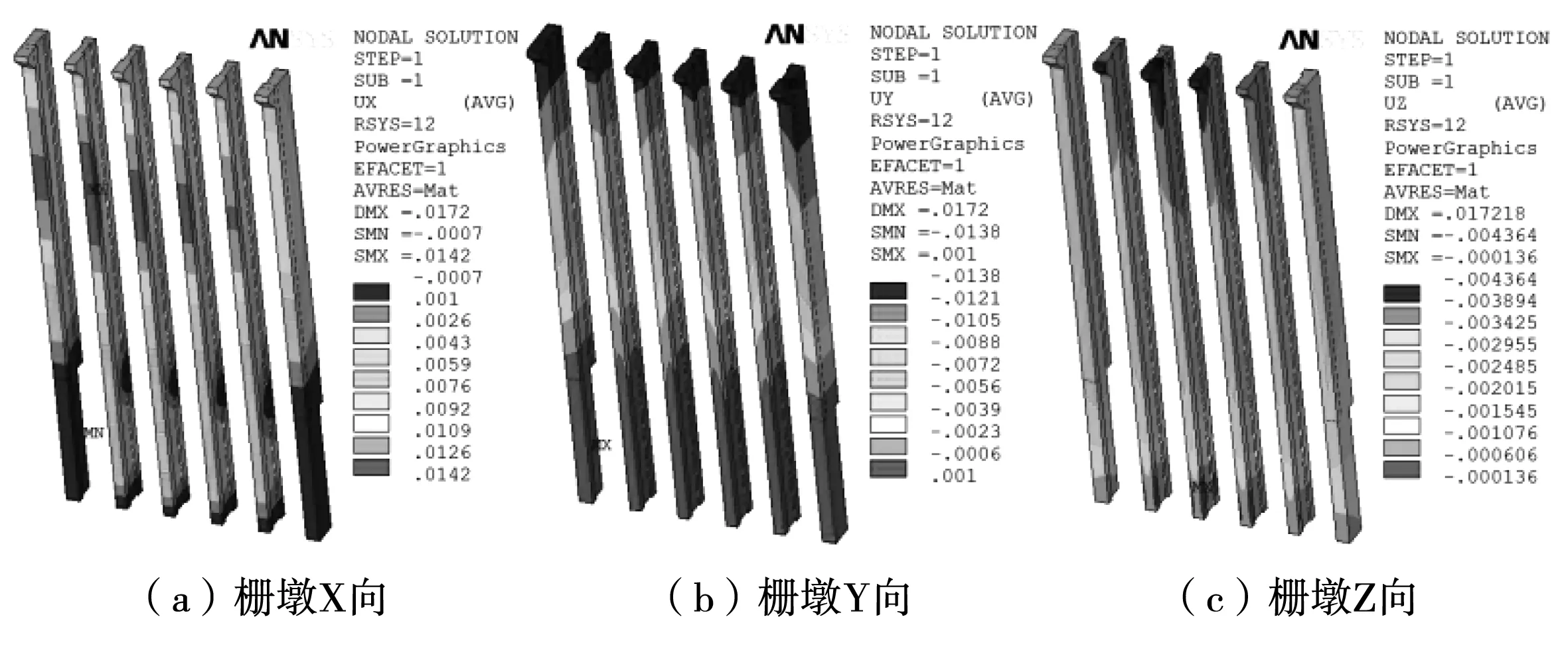
图13 各特征部位位移响应特征

5 结 论

1) 纵梁最大拉应力与截面高度参数为正相关关系；但栅墩承台最大拉应力与截面高度并无显著关联性，各截面高度下均稳定在9 MPa；腰墙上最大拉应力相比前两者均较小，在截面高度1 m后随高度参数逐渐增大。

2) 栅墩X、Y向位移与截面高度参数并无显著关联性，分别稳定在14和13.7 mm；Z向位移随截面高度增大而递减，但降低幅度较小，截面高度为1.5和2 m时的位移值相比高度0.5 m分别降低6.8%和9.1%。

3) 纵梁与腰墙上的最大拉应力均随截面宽度参数增大而稍有增幅，在宽度1.5 m后增长停滞；栅墩承台最大拉应力随截面宽度设计参数增大而递减，宽度1.5和2 m时最大拉应力相比宽度0.5 m时分别降低6.6%、9.8%。

4) 栅墩X、Y、Z向位移随截面宽度设计参数几乎无较大变化，X、Y向位移均稳定在14 mm；Z向位移随宽度参数增大而稍有降低，在宽度2 m时位移相比宽度0.5 m时降低4.6%。

5) 综合截面体型设计参数研究得到，截面积愈大，纵梁拉应力愈大，栅墩承台最大拉应力随截面积增大而递减，腰墙最大拉应力最大不超过3.1 MPa；栅墩X、Y向位移基本不变，分别稳定在14和13.8 mm，Z向位移稍有增大，最大增幅仅为14%；综合各设计参数影响因素确定截面高度、宽度均为0.5 m时，闸墩抗震性能最佳。