河堤极限承载力的有限元分析研究

柏 丽

(辽宁泽龙水利实业有限责任公司，沈阳 110003)

0 前 言

河道堤防的稳定性设计需要对其极限承载力进行综合设计，是河道堤防加固工程最为重要的一项设计指标[1]。对于河道极限承载力的方法主要为两种，一种是采用室内试验测定方法，通过现场取样，在实验室内对其土层的极限承载能力进行测定，这种方式的优点在于较为直观，缺点在于选样的方式和土层的深度对其极限承载力的准确测定影响较大，很难准确对河道堤防的极限承载力进行准确测定[2]。第二种方法为采用弹性模量模型计算方法，通过设定土层的物理力学参数，对河道堤防的极限承载能力进行计算分析，这种方法的缺点在于需要确定较多的参数，但优点在于可以分析计算不同河道堤防设计指标下的极限承载力，当前在许多河道堤防工程设计中得到较为广泛的应用[3-5]。但弹性模量模型的一个局限在于其收敛度不高，在一些工程实例应用中模型求解较为困难，且参数较难获取。有学者针对弹性模量的局限，开展基于有限元的弹性模量计算方法，通过有限元方法对弹性模量的阈值进行优化，提高模型收敛精度，通过实例表明其计算精度要好于传统单一的弹性模量方法。为此文章引入有限元计算方法，以辽宁某河道堤防工程为具体实例，探讨有限元方法在河道堤防极限承载力计算的适用性。研究成果对于该方法推广应用具有重要的参考价值。

1 研究方法

将有限元和传统弹性模量方法进行耦合对其承载比进行计算：

(1)

式中：ηe,i为承载比极限值；Se,i为有限元计算相同时效的堤防承载力，kPa；Se,0为不同有限计算单元的承载比极限值，其中Se,i的计算方程为：

Se,i=f(σij)Se,0=f(σs)

(2)

式中：σ为不同计算有限元的应力值，kPa；σs为强度折减系数。在进行承载比极限值计算基础上，对其均匀度进行计算：

(3)

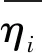
ηmin,i=min(η1,i,η2,i,…ηN,i)

(4)

ηmax,i=max(η1,i,η2,i,…ηN,i)

(5)

(6)

式中：N为有限计算单元的总个数。有限元分析方法对各计算单元的承载比阈值进行优化计算：

η0，i=ηmax,i-di(ηmax,i-ηmin,i)

(7)

式中：η0，i为堤防承载比的标准值。对承载比阈值优化后的弹性模量能量和耗能方程分别进行调整：

(8)

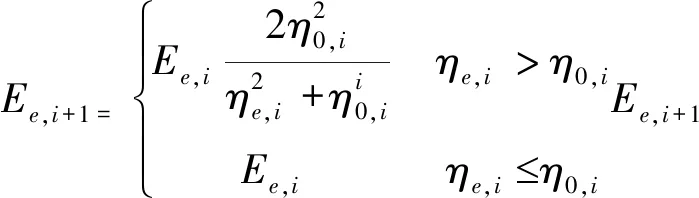
(9)

式中：Ee,i+1、Ee,i分别为第i个和第i+1个计算有限单元的静力荷载，kPa。对上述两个方程进行有限元迭代求解计算：

(10)

式中：PL,i为模型求解的河道堤防的极限承载力，kPa；Pn为荷载基准值。

2 模型应用

2.1 工程概况

文章以辽宁某河道堤防加固工程为分析实例，河道堤防土层的物理力学参数如表1所示。整个河道堤防的长度为3.5km。堤防顶部高程和宽度分别为8.5m和4.5m。河道堤防的坡度比降在1:2.5-1:3之间。采用有限计算单元方法结合河道地形测量数据，将河道堤防段空间离散为123375各计算单元，空间离散见图1所示。

图1 河道堤防的有限计算单元

2.2 极限承载力试验结果

结合原位观测试验方法对各河段堤防不同桩号下的岩体力学参数进行试验测定，并基于岩体力学参数测定结果，对其不同桩号下的承载力极限值进行试验测定，各试验桩号承载力极限值试验测定用于对模型计算精度进行检验。力学参数以及不同桩号的承载力极限值试验测定结果如表2和表3所示。

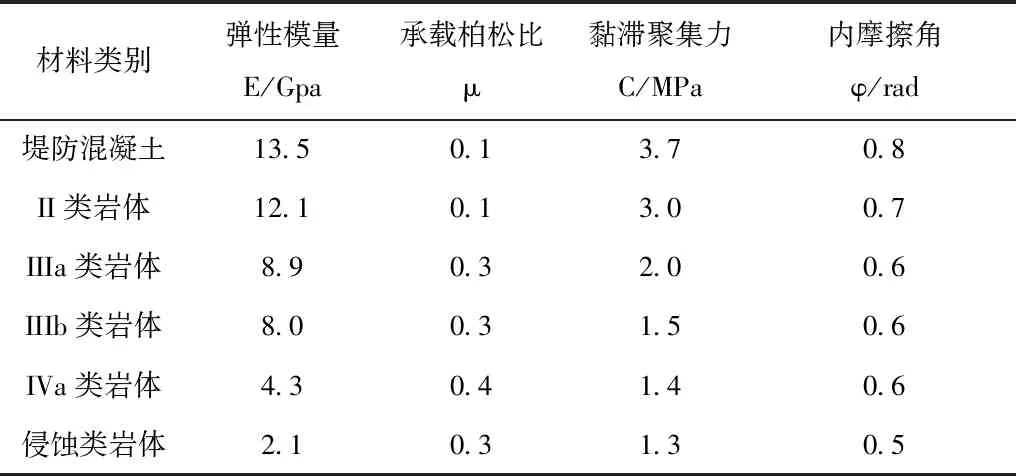
表1 河道堤防土层的物理力学参数

表2 河道堤防不同桩号下极限承载力相关参数测定结果

对于河道堤防极限承载力的测定试验主要通过螺旋桩抗拔进行测定，当螺旋桩顶部位移以及荷载变化点达到最高点位时，河道堤防处于极限承载状态。从河道极限承载力试验测定结果可看出，当1#螺旋桩的钻孔深度达到4.16m时，其极限位移处于最高点为1.55m，极限承载力为75.99KN，2#螺旋桩的钻孔深度达到4.61m时，其极限位移处于最高点为1.65m，其极限承载力测定值为80.33KN，从各螺旋桩的极限承载力测定结果可看出，钻孔深度对其顶部位移和荷载变化影响相对较小，判定的河道堤防的极限承载力只和其顶部位移具有较为直接的联系。3#和4#螺旋桩钻孔深度均高于5.0m，其相比于1#和2#螺旋桩，较容易出现失稳现象，其极限承载力也要小于1#和2#螺旋桩的极限承载力。河道堤防计算的极限承载比和试验测定的极限承载比的总体误差要低于15%，误差产生的原因主要为堤防基准面和实际基准面之间存在一定的差异，使得计算的极限承载比和实际测定的承载比存在一定的误差。

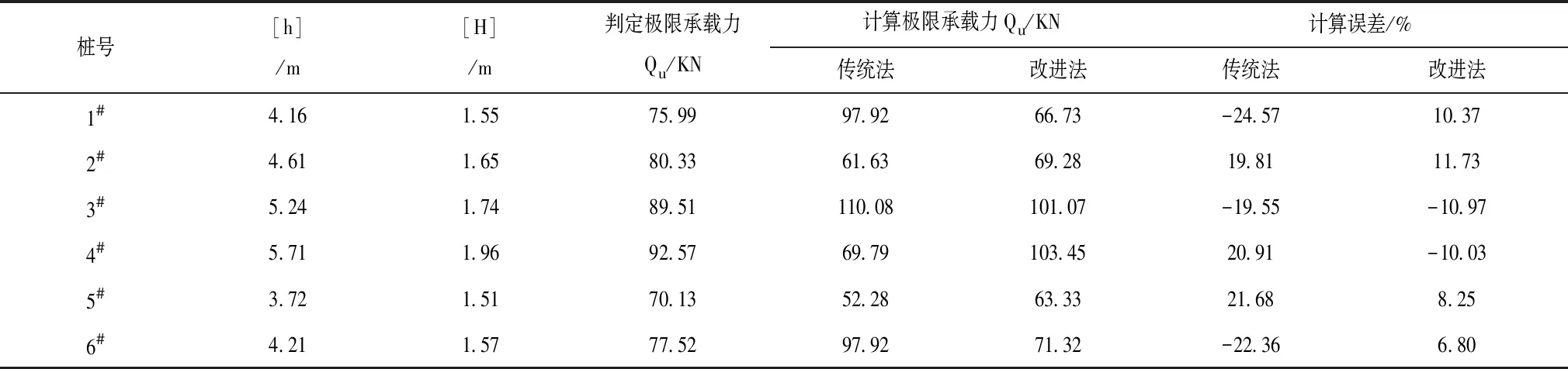
表3 河道堤防不同桩号下的极限承载力试验测定值

2.3 不同方法计算的极限承载力误差对比

在研究河道堤防极限承载力试验测定的基础上，将试验测定的数据作为模型误差验证数据，分别采用传统弹性模量和基于有限元的计算方法对河道堤防的极限承载力进行计算，对比两种方法对极限承载比计算的适用性，结果如图2所示。

有限元计算方法 传统弹性模量方法

从对比分析结果可看出，基于有限元的分析方法由于对极限承载比阈值进行优化，使得其不同迭代计算步长下的模型求解收敛度要好于传统弹性模型计算方法下的收敛度，采用有限元计算河道堤防的极限承载力时，当迭代计算补偿为15次时，其极限承载比计算方差达到最低值，表明模型收敛程度较低，取得最优解。而对于传统弹性模量方法而言，当计算迭代步长为22次时，其极限承载收敛度方差最低，模型迭代计算结束。这主要是因为有限元方法通过离散计算单元，调整和优化承载比参数的阈值，加速了模型求解的收敛度，因此其计算误差要好于传统弹性模量计算方法。

3 结 论

1)当螺旋桩顶部位移以及荷载变化点达到最高点位时，河道堤防处于极限承载状态。河道堤防计算的极限承载比和试验测定的极限承载比的总体误差要低于15%，误差产生的原因主要为堤防基准面和实际基准面之间存在一定的差异，使得计算的极限承载比和实际测定的承载比存在一定的误差。

2)有限元方法通过离散计算单元，调整和优化承载比参数的阈值，加速了模型求解的收敛度，因此其计算误差要好于传统弹性模量计算方法。