基于ADAFSA-BP的概率积分法预计参数研究

郑文博，余学祥，赵祥硕，杨邵文

（1.安徽理工大学 空间信息与测绘工程学院，安徽 淮南232001；2.矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室，安徽淮南232001；3.矿区环境与灾害协同监测煤炭行业工程研究中心，安徽淮南232001）

随着经济不断发展，煤炭的需求量也日益增加，导致地下开采加剧，这不仅影响矿区安全［1］，而且对矿区周边环境也有不利影响，因此对矿区进行开采沉陷的预测工作显得尤为重要。

常见的开采沉陷预测方法有力学模型预计［2］、时间函数模型预计［3］和概率积分法模型预计［4］。概率积分法的优势是计算方便且精度高，它的预计参数可以通过实测数据+优化算法、机器学习或者覆岩性质求解［5］。但实测数据解算成本较高，并且不能在开采前获取。覆岩求解的过程较为复杂，机器学习法求参则较为简单并且预测精度可靠［6］。常用的机器学习为BP神经网络，BP神经网络非线性拟合效果好，但初始权值和阈值的选择存在盲目性，会影响到模型的预测精度和收敛速度。文献［7-8］指出GA-BP神经网络进一步提升了神经网络求参的精度。

人工鱼群算法具有全局搜索能力较强，局部搜索能力较弱的特点。故本文建立ADAFSA-BP模型、普通BP模型、GA-BP模型进行求参精度分析，探究ADAFSA-BP模型求解概率积分法预计参数的可靠性。

1 地质采矿条件与概率积分法预计参数的关联分析

概率积分法的预计参数有8个，本文研究其中的4个，包括下沉系数q，主要影响角正切值tan B，开采影响传播角 θ、水平移动系数 b［9］。

1.1 下沉系数q

下沉系数是地表最大下沉值与采厚和煤层倾角余弦值乘积的比值［9］。根据文献［9］下沉系数的经验公式为：

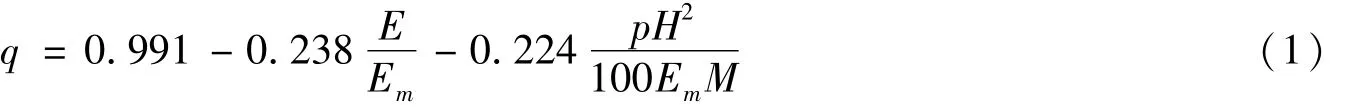
式中，E为岩体综合形变模量，Em为中硬岩体形变模量，p为岩体的平均质量密度，M为开采厚度，H为平均采深。

1.2 主要影响角正切值tan B

主要影响角正切值是走向主断面上，走向边界开采深度与其主要影响半径之比［9］。根据文献［9］其经验公式为：

式中，a为煤层倾角，h为松散层厚度，D为开采宽度。

1.3 开采影响传播角θ

开采影响传播角是指倾向主断面上，开采边界和地表下沉曲线拐点的连线与水平煤层在下山方向的夹角［9］。根据文献［9］其经验公式为：

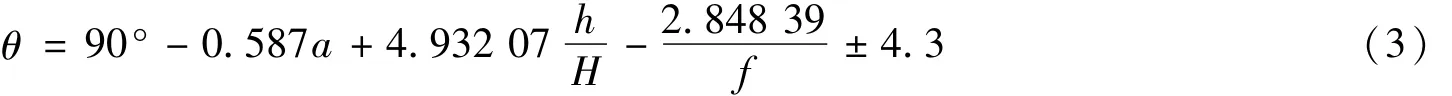
式中，h为松散层厚度，f为上覆岩石平均坚固性系数。

1.4 水平移动系数b

水平移动系数是水平煤层或近水平煤层在达到充分采动时地表最大水平移动与地表最大下沉之比［9］。根据文献［9］其经验公式为：

通过上述分析，可以得出概率积分法预计参数与开采厚度M、平均采深H、采动程度D/H、松散层厚度h和上覆岩石平均坚固性系数f等地质采矿条件有关联，为本文通过地质采矿条件预测概率积分法预计参数提供了理论支撑。

2 基于改进鱼群算法优化的BP神经网络

2.1 BP神经网络

BP神经网络［10-11］是一种误差逆向传播算法，其理解方式就是多层感知机之间信息的传递，通过输入层向前传递信息，在输出层根据求得的损失函数情况，进行误差的反向传播，当传入到输入层后进行各节点的权重调整再循环上述操作，不断迭代直到误差满足精度要求为止。其网络结构如图1所示。

设隐含层某一节点的输出为y，其表达式为：

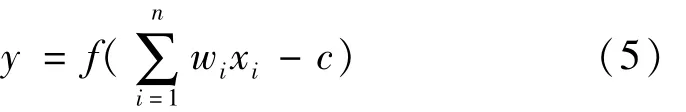
式中，f为激活函数，目前常用的激活函数有sigmoid函数、relu函数、tanh函数，wi为上层输入值各节点所占权重，c为阈值，i=1，2，…N。

通过式（5）不断进行信号传递直到输出层，此时设输出层的数值为a，可列出损失函数方程：

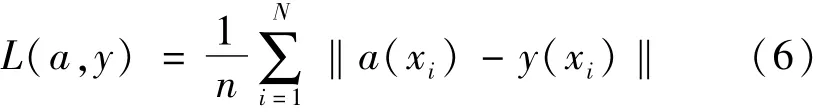
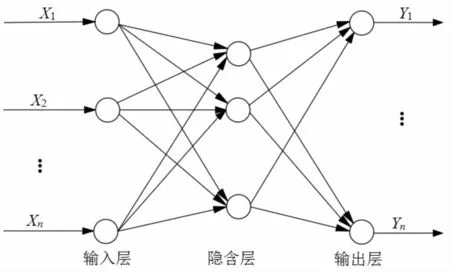
图1 BP神经网络

式中，y为输出层实际值。

上述过程为正向传播，反向传播是根据输出层误差依据梯度下降法调整权重和阈值，其具体表示为：

式中，λ为学习速度，它决定了神经网络收敛的快慢。

通过上述过程，以梯度下降法为依据不断调整网络隐含层和输出层的权重和阈值，理论上最终可以得到满足精度要求的模型输出值。但BP神经网络预测精度受初始权重和阈值的影响较大，实际应用中很难通过经验获得最优初始值。因此本文采用改进人工鱼群算法寻找BP神经网络的最优初始权重和阈值。

2.2 人工鱼群算法

人工鱼群算法是李晓磊博士于2002年提出的基于动物行为的群体智能优化算法［12-13］。这种算法是通过模拟鱼类的行为在搜索空间内进行寻优。

假设当前人工鱼群的状态为X=（x1，x2，…xn），Y=f（X）为每条人工鱼对应的食物浓度，鱼群算法食物浓度计算方式为神经网络所有训练集预测值与真值绝对误差平方和的均值的倒数，f为目标函数，δ为拥挤度，S为移动步长，V为鱼的视野范围，try＿number为最大尝试次数，其计算过程如下：

2.2.1 觅食行为

假设人工鱼现在的状态是Xi，在视野范围V内存在一个Xj的随机状态，有：

式中，rand（）为（0，1）的随机数。

当Xj处的食物浓度大于Xi处时，觅食行为根据式（9）向前移动，否则重新选择随机状态，继续进行食物浓度判断，重复次数达到try＿number后若仍然没有移动，就按照式（8）随机移动。

2.2.2 聚群行为

假设人工鱼群探索范围内的伙伴数为n，中心位置为Xc，若Yc/n＞δYi，表示该位置食物浓度高且不

2.2.3 追尾行为

同聚群行为类似，判定条件变为Yz/n＞δYm，Xz是视野范围内能找到的浓度最大Yz的位置，则按照式（11）向前移动，如果不满足判定条件就执行觅食行为。拥挤，此时可以按照式（10）向中心位置移动，如果不满足上述不等式条件就执行觅食行为。

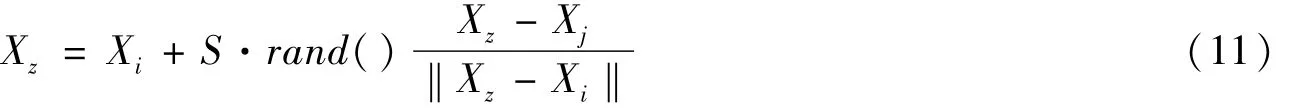
2.2.4 随机行为

随机行为其实是觅食行为在最大尝试次数以后仍没有移动时采取的行为。

2.3 改进人工鱼群

人工鱼群算法全局搜索能力较强，局部搜索能力较弱，非线性规划函数局部搜索能力较强，它能完美弥补人工鱼群算法的不足。当迭代次数达到10的倍数时，将此状态的鱼群代入到非线性规划函数中（本文采用Matlab最优化工具箱中的fmincon函数），去寻找局部最优食物浓度，然后将得到的局部最优解作为新的鱼群个体代入到原鱼群中继续计算。ADAFSA-BP模型的流程图见图2。

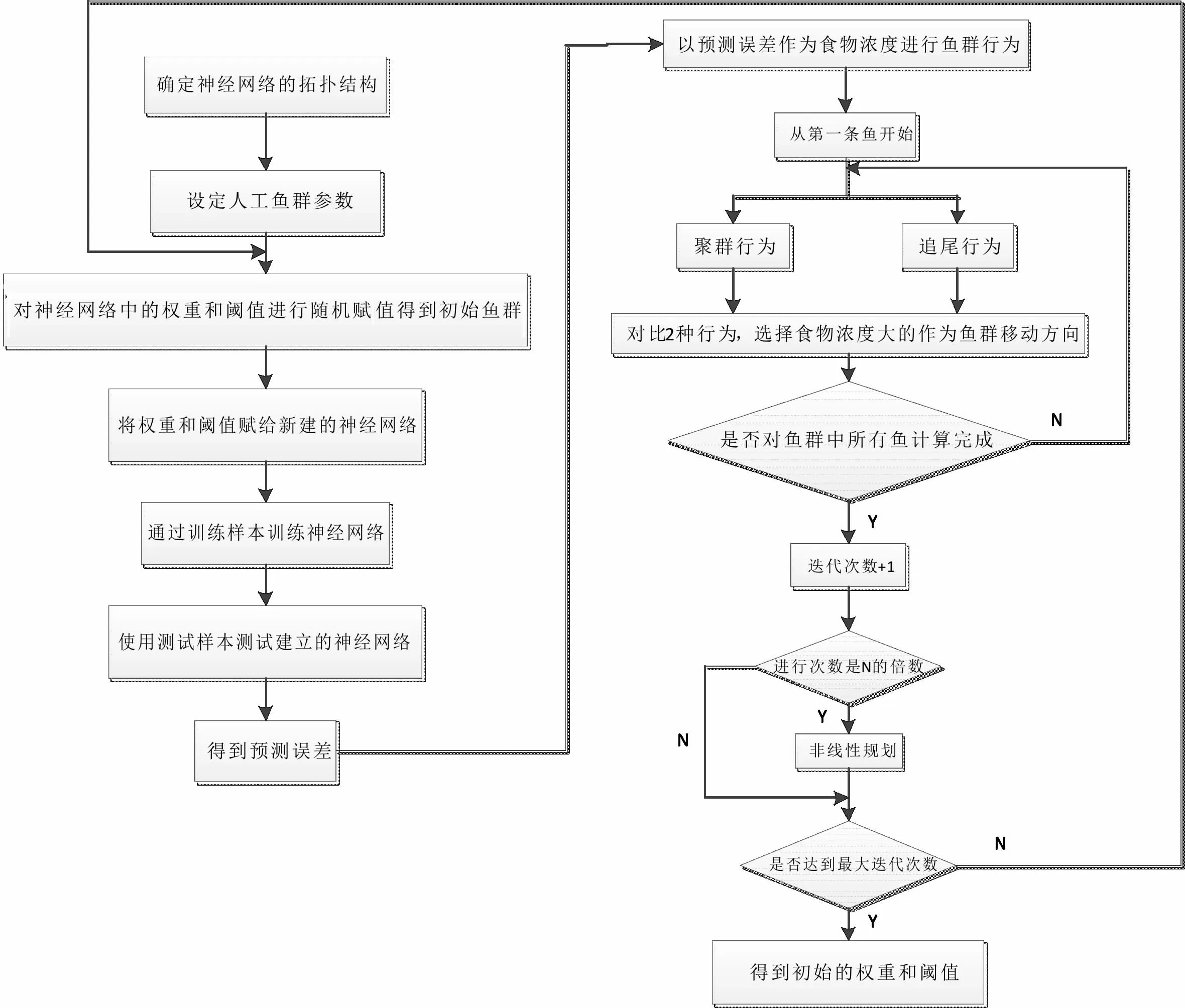
图2 ADAFSA-BP模型流程图

具体操作：将迭代后鱼群作为函数初始输入，神经网络所有训练集预测值与真值绝对误差平方和的均值为fmincon的目标函数（因为fmincon函数的功能是求解局部最小值），将得到的解的倒数作为局部最优食物浓度与此时的鱼群最优食物浓度进行比较，如果局部解的食物浓度高，则用局部解的人工鱼代替当前鱼群中的最优人工鱼，并对新鱼群继续进行迭代，如此反复直到满足最大迭代次数。

3 案例与分析

3.1 ADAFSA-BP模型的构建

以文献［5］中数据为依据，取其中的40个工作面数据进行研究，选取其中的37组数据作为训练集（见表1），剩下的3组数据作为测试集。选取地质采矿条件走向宽深比D1/H、倾向宽深比D3/H、开采厚度M、煤层倾角a、平均采深H、推进速度v、覆岩平均坚固系数f、松散层厚度h，这8个参数作为模型的输入。以下沉系数q、主要影响角正切tanb、最大下沉角θ、水平移动系数b，作为输出。根据文献［14］的结果显示，模型的多输入单输出效果比多输入多输出效果好，参考该结论每次建模只预测一个概率积分法预计参数。BP神经网络的隐含层激活函数采用tanh函数，输出层激活函数采用绝对误差平方和的均值。对于4个预计参数的网络拓扑结构，隐含层的节点数分别设为：13、17、14、11。

表1 训练集数据

由于案例中不同数据之间的取值范围差别较大，直接代入模型会对其预测精度和收敛速度产生较大影响，为了消除这种影响采用Matlab中的mapminmax函数对输入输出数据进行归一化处理。

分别建立起BP模型、GA-BP模型、ADAFSA-BP模型。在本次实验中遗传优化算法的参数设置为：迭代次数设为300，种群数量设为40，取二进制编码，代沟取0.9，交叉概率取0.85，变异概率取0.02。ADAFSA优化算法的参数设置为：人工鱼群个体数N=50，移动步长S=0.3，视野范围V=2.5，最大尝试次数try＿number=60，拥挤度σ=0.721，最大迭代次数M=270。GA优化算法采用谢菲尔德遗传算法工具箱实现，其目标函数值越小适应度值越大，故目标函数（ADAFSA中称为食物浓度）可设为神经网络所有训练集预测值与真值绝对误差平方和的均值。

3.2 误差分析

将训练集代入三种模型完成神经网络的训练，然后再将测试集代入到训练好的神经网络中，得到的预测结果分析见表2、表3。根据表2、表3中的数据可以看出，ADAFSA-BP模型4个预计参数的平均相对误差分别为9.44%、8.62%、3.29%、6.85%。该模型4个参数的平均相对误差都低于BP模型，与GA-BP模型相比较除了下沉系数预测误差偏大外，另外3个参数的预测精度都是ADAFSA-BP模型预测的平均相对误差更低些。

3.3 训练样本数量对模型求参精度的影响

为了进一步研究改进鱼群算法优化BP神经网络在小数据量学习方面的效果。分析三种模型在训练集数量随机减少2、4、6个情况下模型求参精度的波动情况，为尽可能消除偶然性，预测模型平均相对误差取10次模型运算得到的预测精度的平均值，其结果对比见表4。

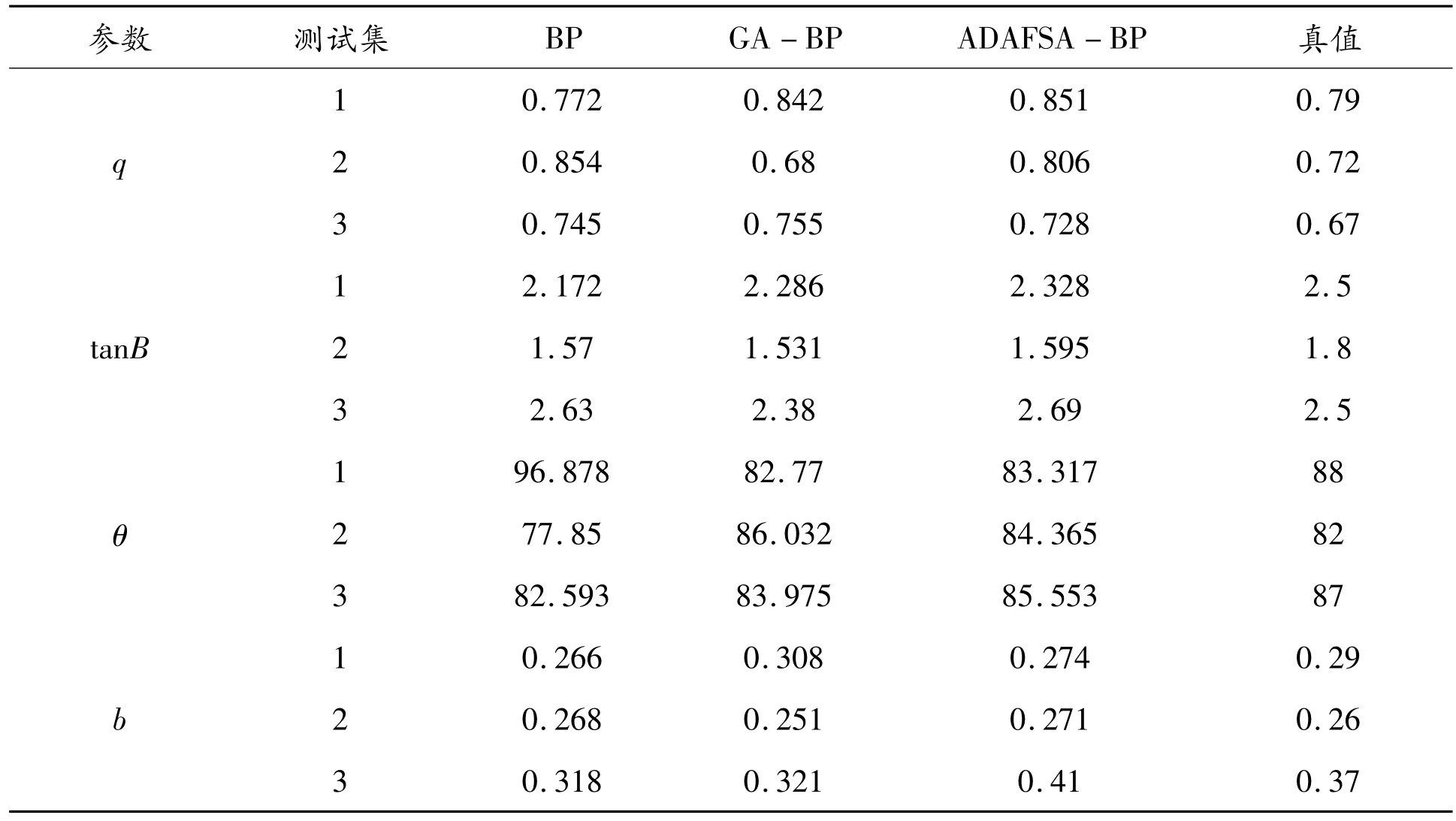
表2 三种神经网络的预测数据对比

表3 三种神经网络的预测精度对比

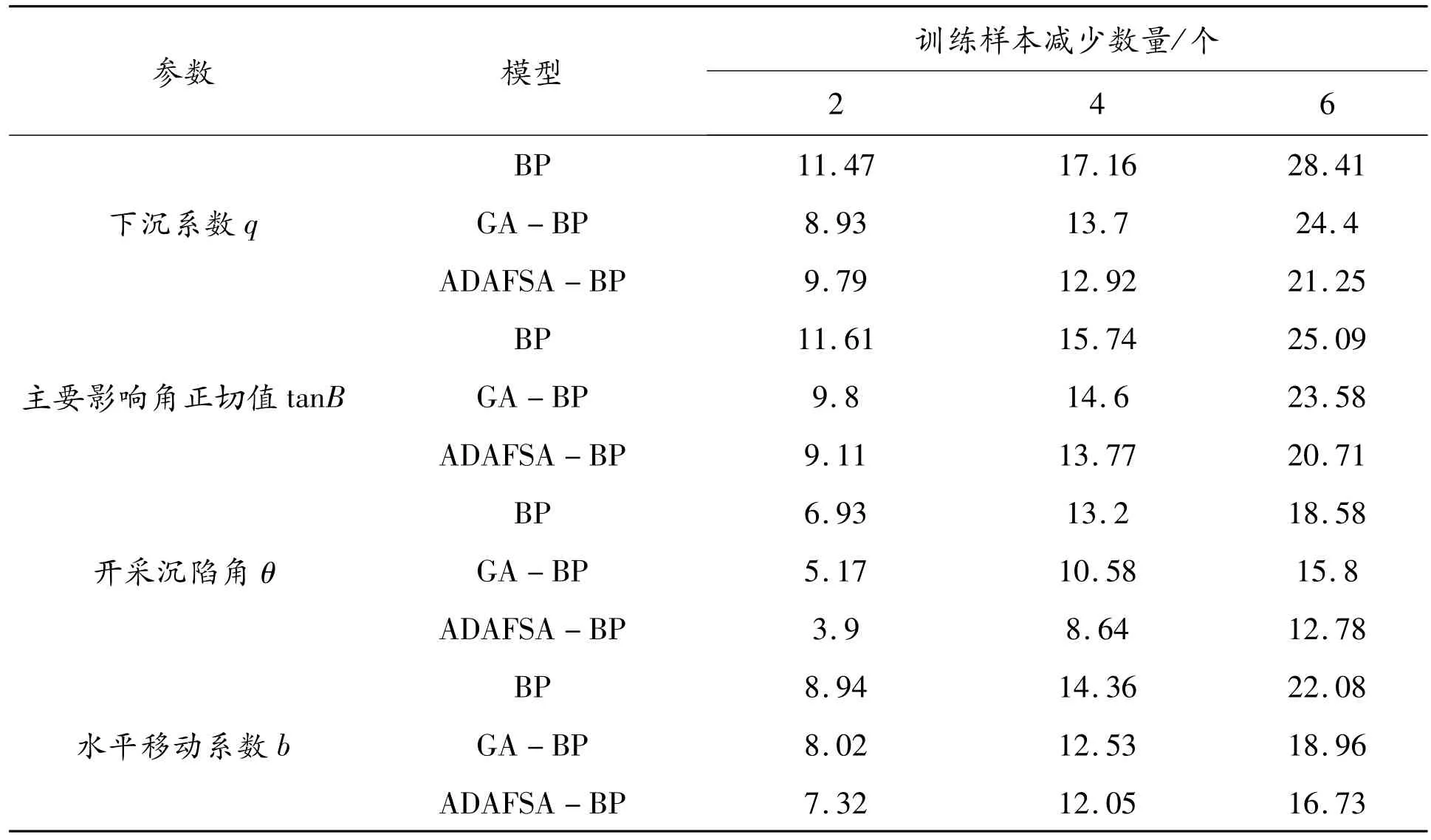
表4 训练样本不同情况下的预测精度（预测模型平均相对误差） %

从表4可以看出，当样本数量减少2个时，三种模型的误差变化量都很小，当样本减少4个和6个时，误差显著增大，误差增大幅度为BP＞GA-BP＞ADAFSA-BP，说明改进鱼群优化BP神经网络模型相比于另外两种模型在小数据量学习方面效果较好。

4 结论

为了提高概率积分法预计参数的准确性，提出改进的鱼群算法（ADAFSA），建立ADAFSA-BP概率积分法预计模型。以我国典型的40个工作面地质采矿条件为例，分别建立BP模型、GA-BP模型、ADAFSA-BP模型并进行精度分析。结果表明：ADAFSA-BP模型预测的4个参数平均相对误差都低于10%且都优于BP模型，与GA-BP模型相比除了在下沉系数上的误差偏大，另外3个预计参数的预测精度都优于GA-BP模型。在训练样本减少的情况下，ADAFSA-BP模型的小数据量学习效果更好。这说明改进鱼群算法优化BP神经网络具有良好的拟合效果，这对于获取待开采区域精度较高的概率积分法预计参数具有良好的指导作用。