基于粒子群算法的变电站巡检机器人运行功率分配

杨希磊，王哲斐

（1.国网上海市电力公司嘉定供电公司，上海200000；2.上海四量电子科技有限公司，上海201315）

0 引言

运行状态巡检是保证电力设备正常运行的有效手段［1-10］。随着人工智能技术的不断发展，变电站内的人工设备巡视工作已经逐渐被智能巡检机器人所替代［11-14］。智能巡检机器人采用充电的方式供能，可完成设备红外测温、表计读取、设备状态识别等功能，如图1所示。

220 kV及以上的变电站占地面积大，设备数量多，完成一次精确巡检需要较长时间［15-18］。为了保证正常的巡检频次，需要在巡检任务量不变的情况下缩短巡检机器人巡检时间。因此，本文充分考虑机器人的运行速度、运行功率、充电时间等因素，提出了目标为巡检时间最短的变电站巡检机器人功率分配模型，并使用粒子群优化算法进行求解，以得到巡检时间最短的机器人运行功率分配方式，实现巡检时间缩短的目标［19-21］。

1 总体思路

本文涉及的变电站智能巡检机器人内置路径规划算法，当巡检任务发出后，即可自动计算完成巡检任务的最短路径，如图2所示。

图1 智能巡检机器人及功能展示Fig.1 Intelligent inspection robot and function display

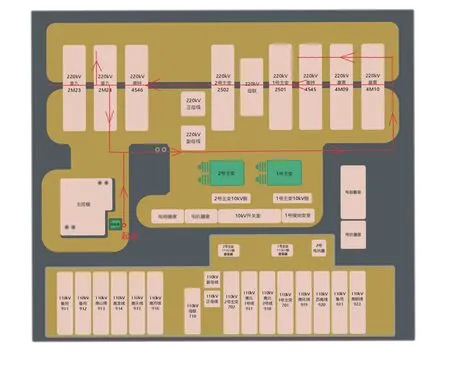
图2 智能巡检机器人最优巡检路径规划Fig.2 Optimal inspection path planning of intelligent inspection robot

因此，对于一个巡检任务而言，机器人的巡检路径长度已经优化为最短，要减少机器人的巡检时间，只能从机器人的运动速度入手。本文设计的巡检机器人内置低、中、高三档（1.2/1.0/0.8 m/s）运行速度，可以在参数设置界面灵活设置3 挡运行速度的比例，巡检机器人参数及运行工况如表1所示。

但是，由于机器人携带的电量是一定的，持续高速运动会使得机器运转功率维持在高水平。图3展示了机器在运动过程中速度与功率之间的关系，由此可以得出，功率与速度的变化关系并不是线性的，随着速度的不断增加，功率的增加速度是持续变快的。假设机器人的速度为v，功率为P，电量为w，运行时间为t，那么可运行总距离为：

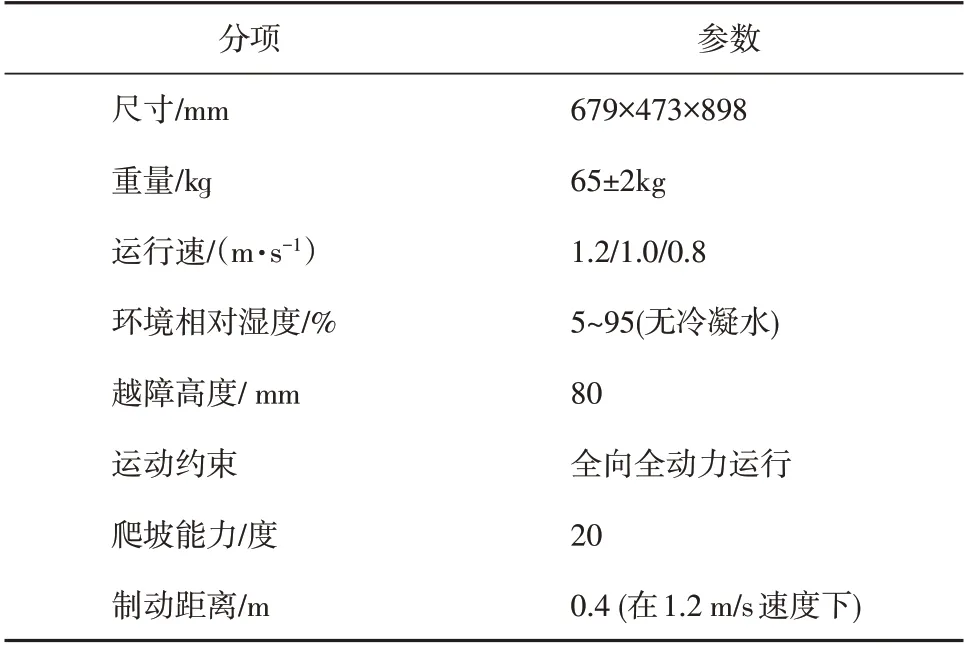
表1 巡检机器人参数及运行工况Table 1 Inspection robot parameters and operating conditions

由式（1）可得，速度与功率之间的变化关系为线性的，那么机器人可以运动的距离只与携带的电量有关。但正如图3所示，随着速度的增加，受阻力增大等因素影响，需要的功率呈类指数形态增长，这就使得过快的运行速度会减少机器人携带同样电量时的运行距离，若机器人电量下降到临界值，就会自动回到充电房充电，耗费较多的时间。

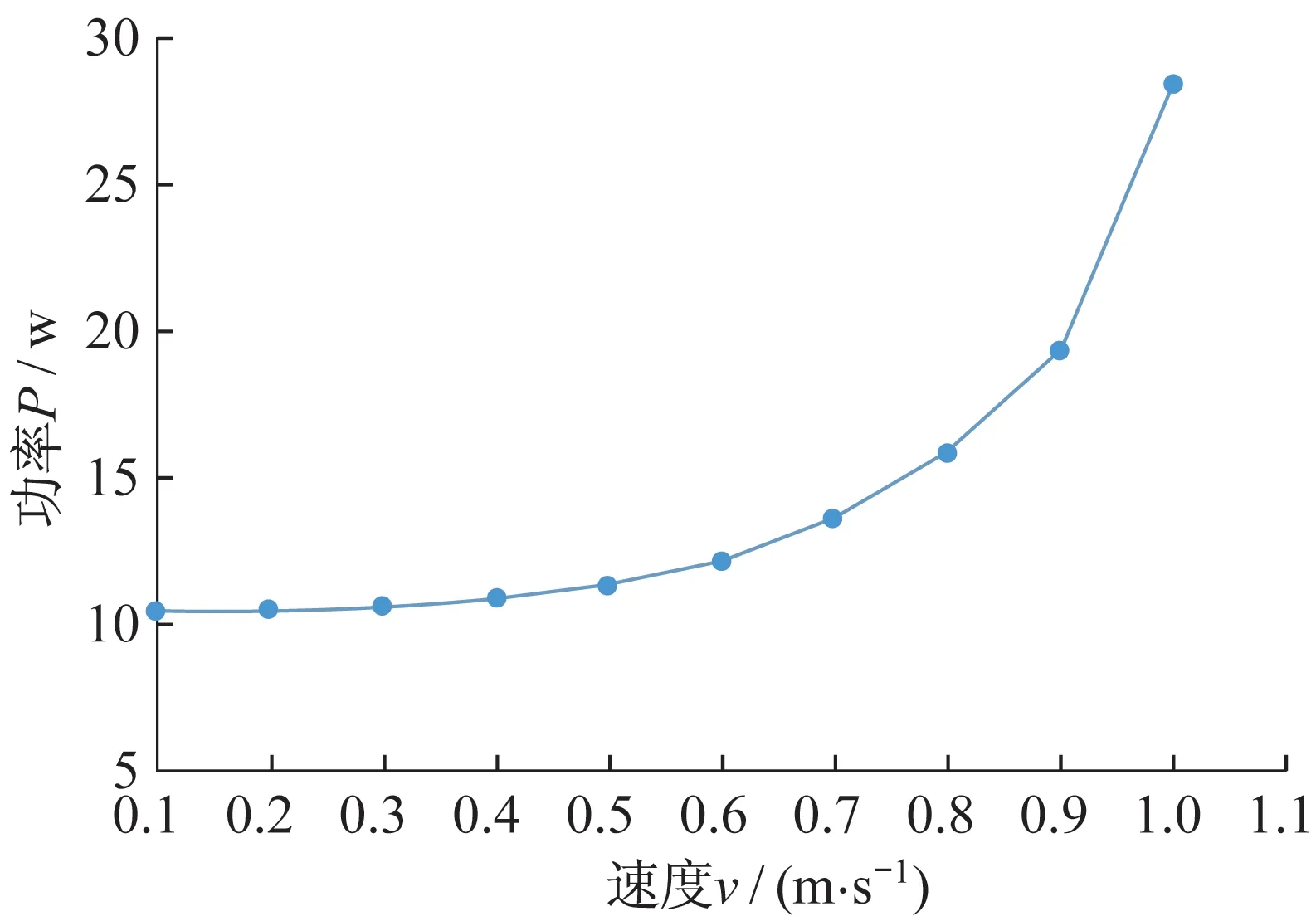
图3 智能巡检机器人速度与功率的关系Fig.3 Relationship between speed and power of intelligent inspection robot

综上所述，在同样的规划路线中执行巡视任务，过量增加机器人运动速度可能会导致机器人因电量消耗过快而回到充电房充电，反而增加了整个巡视任务的执行时间。因此，需要对机器人运动过程中的功率分配进行优化，以实现在同样的工作任务中巡检时间使用最少的目标。

2 变电站巡检机器人运行功率分配模型

2.1 模型函数推导

首先，设机器人完成任务总时间为T，那么本模型的目标函数为：

设机器人低、中、高3 档功率分配占比分别为k1、k2、k3，那么机器人电量耗尽所需时间Tmax和运动长度S1分别为：

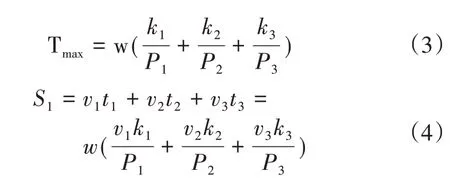
式（3）、式（4）中，机器人运动3 档速度为v1、v2、v3，对应的3 档功率P1、P2、P3，机器人从充电临界值到充满电所需时间为Tc，机器人满电电量为w。机器人完成任务运动路径长度S由机器人内置系统自动计算取得。

当S1＜S时，说明机器人不需要返回充电即可完成巡检任务，则此时消耗的电量w1为：

当S1＞S时，则机器人需要充满电后继续执行任务，并且根据4.2中的测试结果，充满电后机器人可以最高档功率运行直至完成所有巡检任务。此时完成任务所需总时间T为：联立式（2）、式（6）、式（7）构成的分段函数，即可构成本文模型的目标函数。

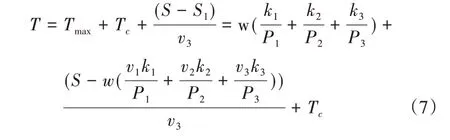
2.2 模型约束条件

首先3档功率分配占比分别为k1、k2、k3需要满足：

机器人在充电过程中不可以自动间断，充满电后才会继续执行任务。

另外根据实验测算，对于路径最长的任务，机器人在能耗经济性最差的情况下，两次充电也足以完成任务。

3 基于粒子群算法的模型求解

粒子群算法（Particle Swarm Optimization，PSO）作为优化模型求解算法，具有收敛速度快，寻优精度高的特点［22-28］。因此，本文选取粒子群算法作为本文模型的求解算法。其迭代公式为：

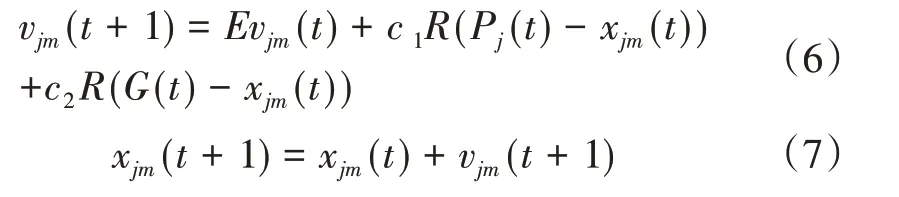
式（6）、式（7）中，在空间中粒子的坐标表示为xj=（xj1，xj2...xjm），其中j表示第j个粒子，m表示粒子的坐标维度。粒子的速度则表示为vi（vi1，vi2...vim），这里的粒子速度表示算法在每一次的迭代过程中该粒子移动的距离。另外，Pj，G分别表示j粒子局部最优值以及所有粒子的全局极值，t表示迭代的次数。c1、c2表示加速系数，E表示权重系数，R为随机数。

权重系数E采用惯性权值，其表达式为：

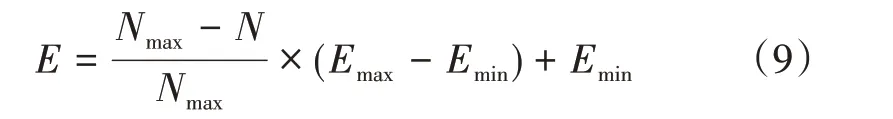
式（9）中，Emax与Emin分别表示E值的初值与终值，N表示目前的迭代次数，Nmax表示设定的迭代次数最大值。

使用惯性权值的好处是，在算法迭代的开始阶段使用大步长加快搜索速度，在迭代后期缩小搜索步长，防止错过最优值。这样既加快了寻优速度，又兼顾了寻优精度。

对于本文的问题求解，待优化变量为k1、k2、k3，因此粒子的维度设置为3。粒子群算法其余参数初始化设置为：加速系数c1、c2取为2.0，Emax与Emin分别取为1.2和0.8，最大迭代次数设置为80次，粒子数设为40。初始化设置完毕后，输入模型目标函数以及约束条件，即可迭代求解，直到目标值连续5 次迭代及以上不发生变化，则最优值求解完成。

4 实验验证

为了验证本文模型和求解算法的有效性，设计了实验进行有效性验证。本文针对3类巡检任务：35 kV设备区巡检、220 kV设备区巡检以及全站巡检进行了30 次巡检实验。在实验场地中，220 kV 设备区共有6个220 kV 出线间隔、2 个主变高压侧间隔、1 个母联间隔、2 个母线间隔；110 kV 设备区共有12 个110 kV 出线间隔、2 个主变中压侧间隔、1 个母联间隔、2 个母线间隔；35 kV 设备区共有20 个35 kV 出线间隔、2 个主变低压侧间隔、1 个母联间隔、4 个电容器间隔、2 个电抗器间隔。在实验过程中，巡检机器人会对所有被测间隔的测温点、表计、开合状态进行测量，实验结果如表2和图4所示。

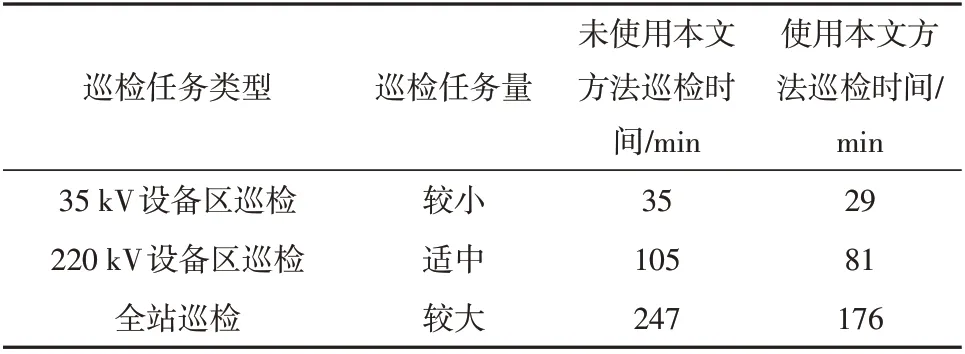
表2 巡检实验结果Table 2 patrol test results

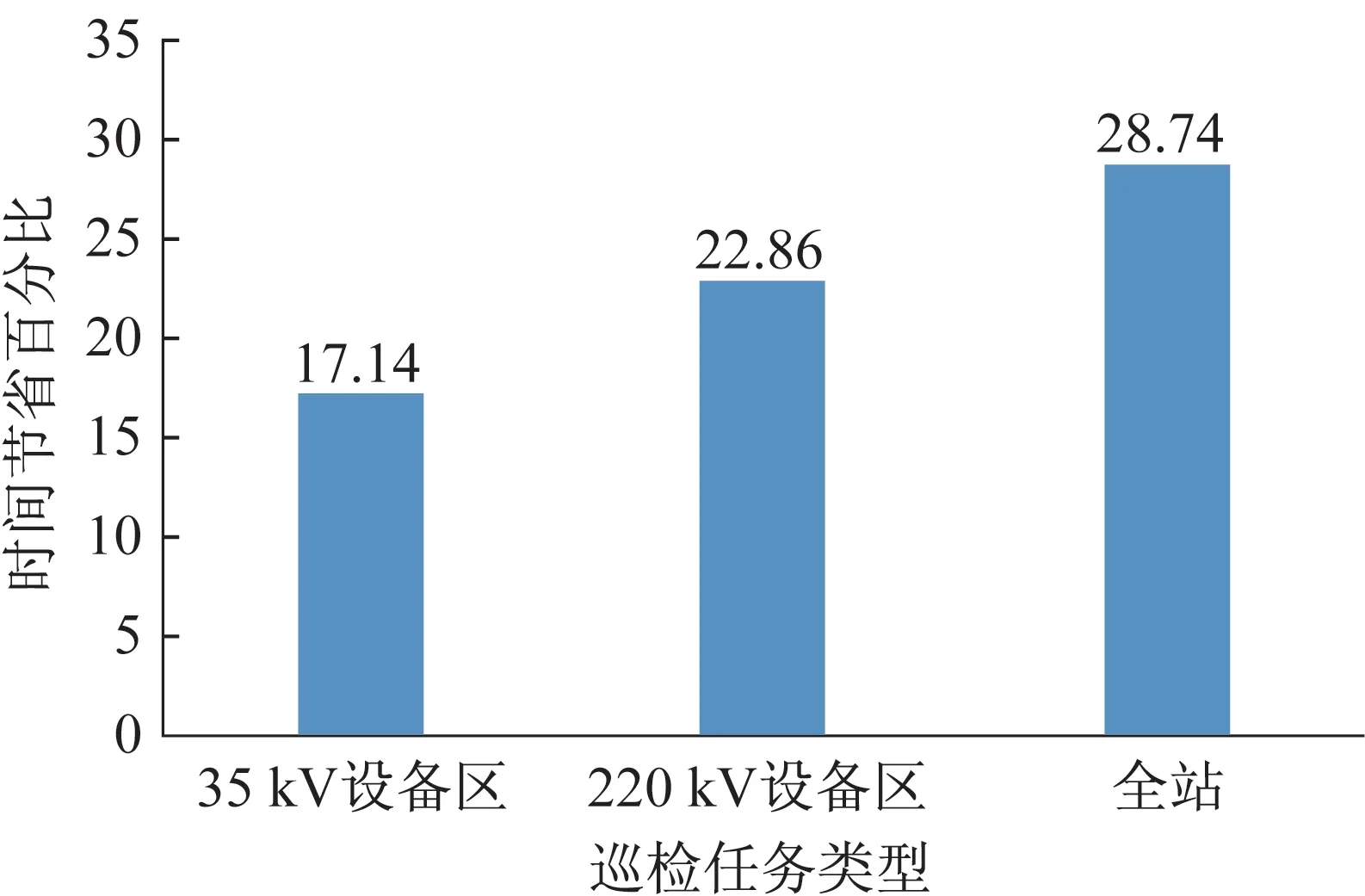
图4 优化后巡检时间减少百分比Fig.4 Percentage reduction of patrol time after optimization

从结果可以看出，本文优化模型应用后，巡检任务的执行时间显著减少，并且时间减少的比例随着任务量增加而上升，全站巡检可节省任务执行时间28.74%，验证了本文方法的有效性。

同时，本文使用较为主流的遗传优化算法（Genetic Algorithm，GA）［29-30］与本文使用的粒子群算法进行了算法对比，两种算法针对本文模型的迭代计算结果如图5所示。

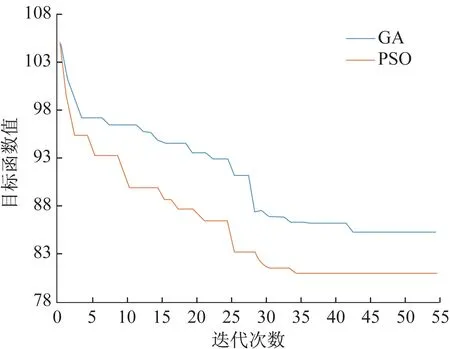
图5 模型求解算法性能对比Fig.5 Performance comparison of model solving algorithms

图5 中以220 kV 设备区巡检任务为例，利用PSO和GA 两种算法进行机器人功率优化分配，记录了算法迭代过程。从结果可以看出，本文使用的PSO 算法收敛速度快，并且寻优的精度更高，验证了本模型求解算法的有效性。

5 结语

本文针对变电站巡检机器人巡检工作，提出减少工作时间的优化目标，并从机器人的3 档工作功率入手，提出了变电站巡检机器人运行功率分配模型。该模型通过对机器人功率大小的优化配置，着力降低机器人巡检工作时间。本文使用粒子群算法对模型进行求解，并设计了实验对模型和求解算法的有效性进行验证。从结果中可以可看出，本文的优化模型可节省机器人巡检工作时间15%-30%左右，成效显著。

本文在考虑机器人充电时间时，直接使用了平均充电时间，在函数中设置为常数。在后续的工作中，可以针对机器人的充电时间继续优化、细化模型，使得模型对于机器人巡检工作消耗时间的刻画更为准确。