外形隐身改进对坦克目标电磁散射特性的影响

刘战合， 罗明强， 郭 乐， 田博韬， 罗丽红

(1.郑州航空工业管理学院航空工程学院， 郑州 450046； 2. 郑州航空工业管理学院无人机研究院， 郑州 450046；3.北京航空航天大学航空科学与工程学院， 北京 100191； 4.西北工业大学航空学院， 西安 710072)

随着现代战争对抗手段的持续提升，隐身技术已成为飞行器、兵器、装甲车辆、地面武装等武器系统的重要技术途径[1-4]，以进一步提高己方武装力量的生存能力或突防能力[5-8]。隐身技术一般是指通过主动或被动技术来降低敌方探测或识别的信号，随着探测技术的快速提高，将面临雷达、红外、声、可见光等多种探测器的综合威胁[5,9]。

坦克是地面武装车辆有效组成部分，是解决地面冲突、局部冲突、反恐冲突的重要攻击性武器之一，多处于战争前沿，对其生存力有更高要求。对地面装甲车辆，雷达隐身性与红外隐身、可见光隐身一起作为重要隐身手段，有必要采用相关隐身改进技术来进一步提高现役或新概念坦克装甲车辆的生存力[5-6]。

以某型常规坦克、隐身坦克为基础，分别建立两类坦克的电磁散射分析模型，采用物理光学法(physical optics,PO)，计算重点作战状态的雷达散射截面(radar cross section，RCS)曲线，以此为基础，计算研究重点威胁角域的RCS均值和减缩值变化规律，通过对比，分析外形隐身改进对坦克电磁散射特性的影响规律，以期为新概念隐身坦克设计提供参考。

1 坦克电磁散射分析模型

为提高地面武装力量的生存力和战斗力，世界各国开展了大量研究，如英国和波兰联合研制的PL-01隐身主战坦克，大大降低了红外和电磁信号。基于PL-01和传统设计坦克，建立了隐身A和常规B电磁分析模型，如图1、图2所示，为便于分析，基本保持两种模型几何尺寸接近，隐身模型A长宽高分别为6.257、3.8、2.433 m，常规模型B长宽高分别为6.162、4.18、2.588 m。采用对比分析方法，研究外形隐身改进对电磁散射特性影响规律。

执行任务中，坦克等装甲车辆将面临来自陆上和空中多种探测器的跟踪、识别，从雷达探测坦克的主要威胁方式出发，为研究外形隐身对坦克的电磁散射特性影响，计算分析时电磁波频率设定为1、3、6、10、15、18 GHz，隐身模型A对应电尺寸分别为20.8、62.6、125.1、208.6、312.9、375.4，常规模型B电尺寸分别为20.5、61.6、123.4、205.4、308.1、369.7，均位于电大尺寸区域(即光学区)，考虑到实际作战情况，入射俯仰角为-5～30°，步长为5°，方位角0～360°。重点关注数个具有重要影响的威胁角域，即坦克前向30°(H-30)、前向60°(H-60)、侧向30°(S-30)、后向30°(T-30)、周向360(W-360)等角域，结合各角域的算术均值变化特性、RCS计算曲线分布特点来分析外形隐身的影响规律。

图1 隐身坦克电磁模型AFig.1 Electromagnetic model of stealth tank A

图2 传统坦克电磁模型BFig.2 Electromagnetic model of conventional tank B

2 电磁散射特性分析方法

2.1 电磁散射计算分析方法

对电大尺寸散射目标，考虑到计算效率和精度，计算方法可分为高频算法和基于并行计算的数值方法。高频算法为近似方法，计算效率高，如物理光学法[1,7]、物理绕射理论、等效电流方法、射线追踪法等，适用于电大尺寸目标。基于并行计算技术的数值方法尽管具有较高的计算精度，但在计算效率上有一定牺牲，对一些复杂结构电大尺寸目标而言，甚至不能得到正确计算结果，如基于矩量法的并行多层快速多极子算法(parallel multilevel fast multipole algorithm,PMLFMA)[9-10]、时域有限差分法(finite difference time domain,FDTD)[11]等。

其中物理光学法和多层快速多极子算法出发点一致，均基于积分方程，有别于多层快速多极子算法考虑所有源、场之间的电磁相互耦合作用，物理光学法仅考虑对电磁影响重要的源、场重合时的强自耦合作用。尽管物理光学法对计算过程有一定的近似处理，但保留了多层快速多极子算法的部分高精度优势，对电大尺寸目标更为适用，可获得较为优秀的计算效率[1,7]。就所研究的坦克装甲类目标，从实际应用角度考虑，为兼顾计算效率和精度，采用物理光学法进行分析。

2.2 外形隐身改进的电磁散射影响分析方法

一般情况下，可通过目标RCS曲线分布特点，结合一定角域内的RCS算术均值或几何均值研究其电磁散射特性，该方法仅在一定程度上反映目标的电磁隐身性能，而缺乏对外形、材料、结构等技术手段产生的隐身改善效果，同时对其在频率、姿态等维度上的电磁影响关系也缺少相应的分析方法。

基于以上考虑，针对坦克装甲类目标，在传统分析方法的基础上，以常规、隐身坦克电磁模型为基础，分析同一角域上两种模型的RCS算术均值或几何均值，通过对比分析，获得隐身坦克电磁模型在该角域上的电磁隐身性能影响规律。

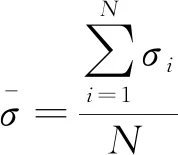
(1)

式(1)中：N为数据采样点数目；σi为第i个入射角的RCS值，dBsm。基于式(1)，定义隐身坦克电磁模型相对于对应常规模型的减缩值为

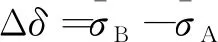
(2)

研究中，选择对应角域为重点关注角域或对研究目标隐身性能有重要影响的角域，一般为前向、后向某角域，如要求全方位角域隐身性能，也可包含其他方位角域。因此，角域的选择与实际研究目标和要求有关。在关注角域内，Δδ>0 dB时，坦克目标外形隐身措施有效，反之，降低了隐身性能，其值反映外形隐身提高程度。

3 两种坦克电磁模型RCS分布特性

隐身模型A通过对车体和炮塔进行外形隐身改进，在一定程度上提高了电磁隐身性能，为分析两种模型RCS曲线分布特性，分别从入射电磁波频率、俯仰角两个维度进行研究。鉴于不同状态的RCS曲线有较为相似的变化规律，仅以频率3、15 GHz(俯仰角0°)的RCS曲线对比来研究频率特性，如图3所示；以俯仰角0°、10°的RCS曲线对比分析来研究俯仰角影响特性，如图4所示。

图3 两种模型的多频RCS曲线Fig.3 RCS curves of two models with different frequency

频率为3、15 GHz时，两种电磁模型均处于高频散射区域，从图3可以看出，两种模型的RCS曲线在周向对称分布有6个大小不一散射波峰，分别位于0°、90°、125°、180°附近范围。前向0°散射波峰为坦克正前向结构(如履带、防浪板、炮塔等)在前向的镜面散射或接近镜面散射的效果，方位角90°上的散射波峰为车体侧面结构的综合作用，包含履带、炮塔侧面、车体等镜面散射，方位角125°左右为炮塔和车体后方斜面的散射影响，后向180°角域为车体后向平面、炮塔后向平面及履带散射作用。

尽管从周向波峰来看，两种电磁模型有较为相似的散射分布特点，但其差异依然较大，说明外形隐身技术对坦克模型的RCS曲线有重要影响。首先，从图3可以看出，采用外形隐身的模型A的RCS散射曲线有明显“内陷”效果，即同一频率下，模型A的散射曲线在不同方位角上有不同程度的降低，说明外形隐身改进可实现较大范围的隐身性能提高。其次，从坦克装甲车辆执行任务角度出发，隐身改进措施重点关注了前向和后向一定角域内的RCS散射幅值，可以看出，在前向较大角域内(甚至可达方位角0°左右60°范围)，模型A明显低于对应模型B的散射曲线，说明在前向坦克隐身性能获得了较大的改进效果，在后向30°域附近，也表现出相似的特性。再次，虽然两种模型在响应位置均有一定散射波峰，但从波峰特点来看，隐身模型A的散射波峰具有波峰较窄、峰值明显较低的特点，尤其在威胁较大的前向和后向位置，对模型A，前向和后向散射波峰，部分原因为炮塔和车体构成了一定的二面角，但该二面角通过水平斜置明显减小了对前向的散射贡献，降低了该方位角下的电磁散射，即波峰较窄、峰值较低。

从频率影响来看，由图3可以看出，频率增加时，两种模型RCS曲线振荡性更加明显，对应方位角上的散射波峰更加尖锐，即波峰变窄，如前向和后向两波峰位置，利于隐身性能的提高。同时，模型A的RCS散射曲线频率增加时有向内收敛的趋势，而模型B有较小的增加，尤其表现在前向角域，说明频率增加时，模型A的外形隐身效果有一定提高，而模型B隐身性能降低。同时可以看出，频率的变化对散射曲线分布影响不大，其RCS散射波峰、波谷位置并未发生实质改变。

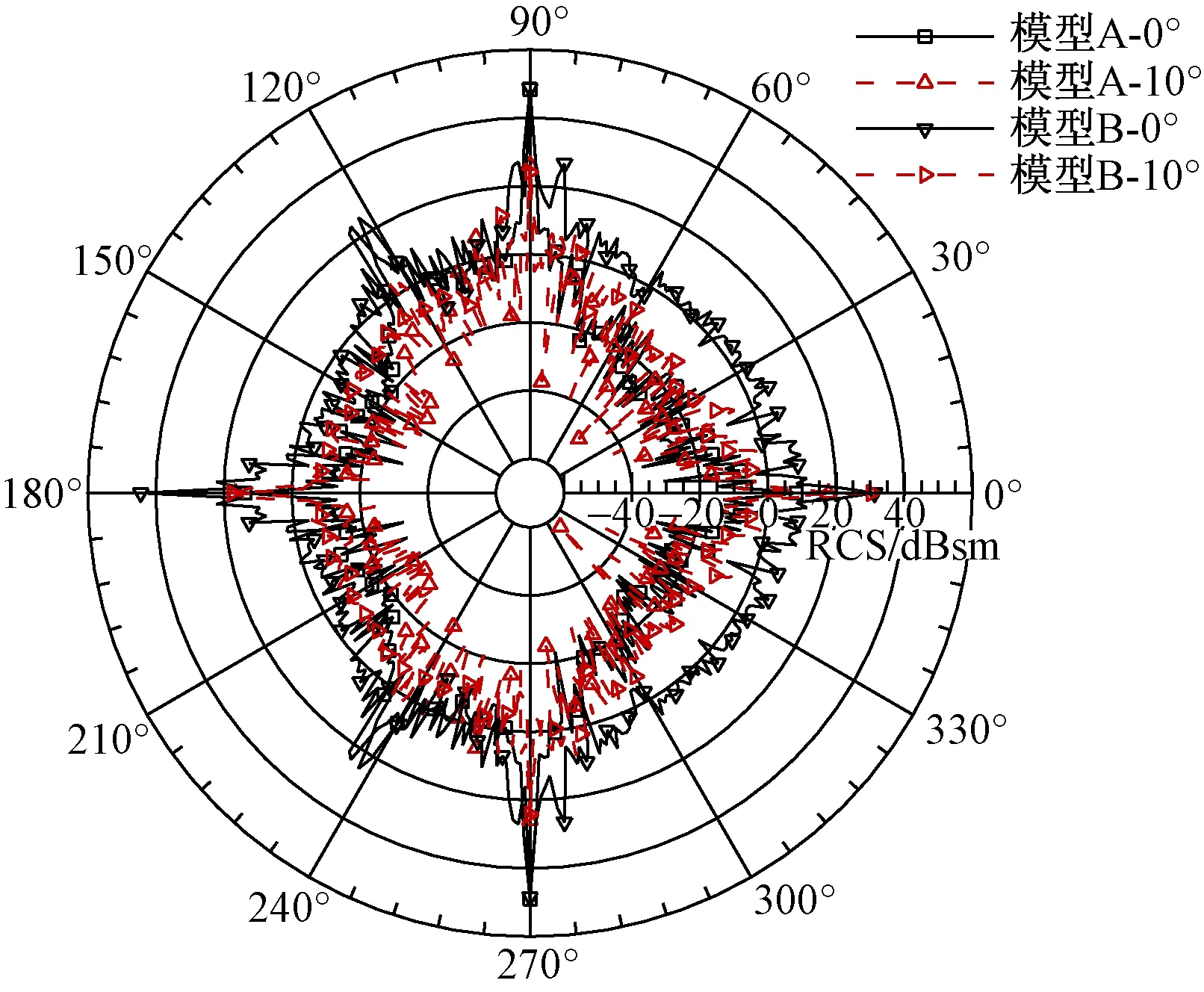
图4 两种模型不同俯仰角的RCS曲线(10 GHz)Fig.4 RCS curves of two models with different pitch angles (10 GHz)

区别于图3的频率特性，由图4可以看出，对10 GHz入射电磁波频率，俯仰角变化时，RCS曲线变化特点不一，对模型A，俯仰角由0°增加至10°时，RCS曲线整体向内收敛，幅值降低，提高了隐身性能，同时，波峰幅值降低、宽度变窄，前向0°、后向180°的峰值明显尖锐化，125°角域附近的波峰消失，利于隐身实现，说明一定的俯仰角对隐身性能有改善效果。对模型B来说，俯仰角增加到10°时，RCS曲线发生较大变化，表现为周向较大范围上有明显的向内收敛趋势，即RCS曲线“内陷”，在前向较大范围角域上，降低幅度达20 dB左右，有助于前向隐身性能的改善；与模型A变化类似，波峰变窄、宽度变窄，在一定程度上提高了对应角域上的隐身性能。同时，与频率特性类似，较小范围的俯仰角变化，并未改变RCS分布特点，仅在幅值、波峰宽度上有一定影响。

基于以上俯仰角特性，可以看出，对模型A，由于在车体、关键部件位置等采用了外形隐身修形，在重点角域上，其RCS有了较好的减缩和控制效果，即一些影响隐身性能的镜面散射、耦合散射等均获得较大较弱，使得模型A在俯仰角改变时，其散射机理并未发生较大改变，因此，散射曲线分布特性具有相似性，尽管RCS有一定降低，但变化较小。而对模型B，由于未采用隐身改进措施，俯仰角从0°增加到10°时，前向、后向结构部件的镜面散射作用明显减弱，对应RCS曲线峰值和幅值均降低。为进一步研究外形隐身改进效果，后续详细研究了俯仰角变化时的RCS减缩值变化特性。

综上，经过对炮塔、车体前向、后向及其他重要结构件的外形隐身改进，在一定程度上降低了RCS的散射强弱程度，并对散射方向和能量进行了合理的控制，有效提高了坦克目标的隐身性能。

4 外形隐身改进的电磁散射影响

在RCS曲线分布分析的基础上，分别计算了两种模型在几个重点角域(H-30、H-60、S-60、T-30、W-360)的RCS均值及相应的减缩值，与上述研究对应，分别从不同频率、俯仰角两方面来研究隐身改进对坦克电磁散射影响规律。

4.1 不同频率电磁散射影响

以俯仰角0°为例，入射频率分为1～18 GHz时隐身模型A不同角域的RCS均值及减缩值变化曲线分别如图5、图6所示。

图5 不同频率RCS均值曲线Fig.5 RCS mean value curves of different frequency

图6 不同频率RCS减缩值变化曲线Fig.6 RCS reduction value curves of different frequency

图5可以看出，对坦克隐身模型A，入射电磁波频率增加时，RCS均值逐渐降低，各向角域均值从大到小依次为S-30、W-360、T-30、H-30、H-60，说明在用外形隐身技术后，坦克具有低的RCS均值特性。结合图3，频率的增加利于隐身性能的提高，频率较低时(1～6 GHz)各角域RCS均值降低较快，频率较大时，降低幅值减小。

从各角域RCS分布来看，隐身模型A在前向角域(H-60、H-30)具有较好的隐身性能，且频率的变化并不影响散射机理的变化。对H-30角域，结合图3散射分布曲线，在前向0°附近角域由于坦克前向平面有一定的接近镜面散射、弱二面角散射产生的散射波峰，提高了该角域内的RCS均值；对H-60角域，由于RCS曲线除去前向0°附近的散射波峰，大部分处于较低水平，提高了该角域内的隐身性能，RCS均值由-10.671 dBsm(1 GHz)降至-20.509 3 dBsm(18 GHz)，说明具有较好的前向隐身性能。在侧向角域(S-30)，频率增加时，散射强度尽管有一定减小，但受侧向平面较大的镜面散射机理影响，降低幅度有效，隐身性能较差。在后向T-30和周向W-360角域，二者RCS均值曲线黏合且变化趋势一致，在T-30角域，由于散射波峰相对常规模型有较大的降低，且影响角域较窄，具有较低的散射强度，隐身性能较好，由-1.094 8 dBsm降至-13.325 2 dBsm；周向W-360角域上RCS为各角域的综合影响，具有较高的隐身性能，由 -4.042 4 dBsm 降低为-12.828 6 dBsm，隐身性能提高。

RCS减缩值可进一步量化研究外形隐身改进措施的电磁散射影响，由图6可以看出，频率增加时，各角域的RCS减缩值均呈振荡性增加趋势，说明外形隐身改进效果在频率增加时更为明显，对1～18 GHz，前向H-60、H-30角域减缩值较大，外形隐身性能效果最好。

由图6可知，RCS减缩值依次从大到小为H-60、H-30、T-30、周向W-360、侧向S-30角域。尽管外形隐身改进后，在前向和后向依然存在一定的镜面散射作用，如前所述，其波峰强度和宽度均变小，有助于隐身性能提高。对前向H-30角域，减缩值在3 GHz时增加较为明显，有较大的振荡性，随后逐渐增加，前向H-60角域上，呈逐渐增加趋势，说明两角域上外形隐身改进效果明显提高，减缩值在13.626～26.771 3 dB。对侧向S-30角域，RCS减缩值也随频率增加而增加，由于隐身模型A采用了平面斜置技术，在一定程度上有助于0°俯仰角下的隐身性能提高，降低了其在侧向产生的镜面散射，结合图3可以看出，波峰宽度和峰值均明显降低，这一特点也表现在其他频率上。对后向T-30角域，与前向H-30角域变化规律相似，均在3 GHz左右有较大增加，在其余频率上逐步增大，后向角域内受散射波峰影响较大，该波峰对频率的变化较为敏感，减缩值变化范围为6.082 9～22.186 7 dB，也表现出了较优秀的隐身改进性能。在周向W-360角域，其变化规律与侧向类似，但其减缩值大小介于前向和侧向之间，说明外形隐身技术可降低周向电磁散射强度，具有一定的全向隐身性能改善。

4.2 不同俯仰角电磁散射影响

入射频率为10 GHz时，俯仰角-5°～30°时隐身模型A不同角域的RCS均值及减缩值变化曲线分别如图7、图8所示。

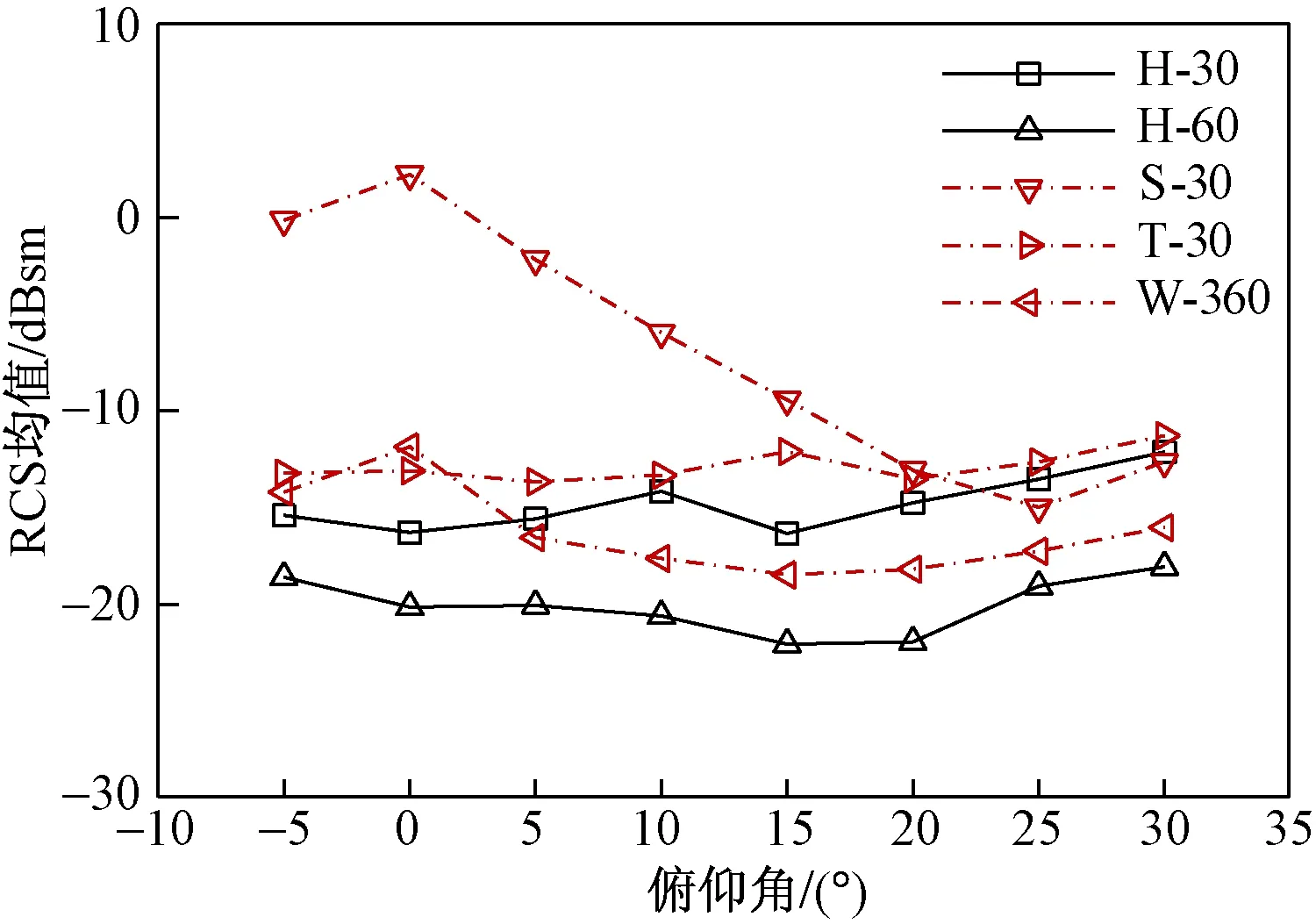
图7 不同俯仰角RCS均值变化曲线Fig.7 RCS mean value curves of different pitch angles

图8 不同俯仰角RCS减缩值变化曲线Fig.8 RCS reduction value curves of different pitch angles

对隐身模型A，由图7可知，俯仰角变化时，除侧向角域S-30之外，其余角域的RCS均值呈振荡趋势。前向H-60和周向W-360角域上，RCS均值先降低后增加，但变化幅值不大，前向H-60上的RCS均值在-22.060 3～-18.608 3 dBsm，周向W-360对应为-18.474 4～-11.855 9 dBsm，说明外形隐身在不同俯仰角上的前向H-60、周向W-360角域上均有明显效果，而一定角域的俯仰角变化未导致明显的电磁散射机理变化。对前向H-30和后向T-30角域，RCS均值呈较弱的振荡增加趋势，但也维持在较低水平，振荡范围-16.346～-11.287 7 dBsm，该角域内隐身性能较H-60角域稍差。对侧向S-30角域，俯仰角增加时，车体侧面镜面散射作用贡献在俯仰角增加时有明显降低，因此，侧向S-30角域上较小迎角时RCS均值较大，而较大迎角时，RCS均值降低，其散射作用减弱，但由于实际作战中，侧向隐身对作战效能的影响较弱，同时需要满足车体结构特性，该角域上隐身性能会受限制，需结合材料涂覆等技术手段来进一步提高。

综上，一定范围的俯仰角变化对隐身模型A的电磁散射特性影响不大，并未引起电磁散射机理的较大改变，主要表现在除侧向S-30角域上，整体来看，外形隐身在-5°～30°俯仰角上在H-30、H-60、T-30、W-360角域上均具有较好的隐身性能，前向H-60隐身性能最优，RCS均值在-20 dBsm左右。

与频率变化关系分析类似，外形隐身改进效果同样对俯仰角由影响，为使得俯仰角在考虑实际作战状态的同时，兼顾更广的研究范围，俯仰角在-5°～30°。图8可以看出，频率10 GHz情况下，俯仰角变化时，呈现以下几个重要特点：一是俯仰角0°各角域RCS减缩值最大，隐身改进效果最好；二是后向T-30角域外，各余角域减缩值在关注俯仰角上均为正值，外形隐身在以上俯仰角上均有效；三是俯仰角增大时(俯仰角大于0°)，RCS减缩值逐渐减小，幅值各部相同。

对前向H-30、H-60角域，图8说明，0°俯仰角左右隐身改进性能最大，受前向峰值影响，H-60角域的RCS减缩值为24.473 4 dB，为各角域、各俯仰角最大值，H-30角域稍小，随着迎角的增大，大迎角下常规模型对应位置镜面散射带来的波峰大大减弱，因此H-30度角域受此影响降低较为明显，但总体来看，俯仰角变化时依然有较好的外形隐身改进效果。对后向T-30角域，俯仰角-5°～10°时，减缩值大于0 dB，15°、20°时接近0 dB，之后小于0 dB，这是由于车体后侧平面采用斜切处理办法，在大于20°出现了较大镜面散射引起，但从俯仰角0°来看，依然有较明显的RCS减缩效果，达到18.262 8 dB左右，该俯仰角附近隐身性能提高较为明显。对侧向S-30和周向W-360角域来说，二者减缩曲线变化趋势一致，俯仰角0°时减缩效果较好，其余俯仰角下减缩值在10 dB左右振荡性减弱，但均有隐身效果，说明较小的俯仰角变化对电磁散射减缩机理的影响不大。

5 结论

为研究外形隐身技术对坦克电磁散射特性的影响，分别建立了隐身、常规坦克电磁模型，采用物理光学法计算了多种状态下的RCS，基于散射曲线的分布规律、RCS均值及其减缩值的变化特性分析，研究了外形隐身对电磁散射特性的影响，得到以下结论。

(1)RCS曲线影响：频率和俯仰角变化时，外形隐身对RCS曲线均有明显影响，改进后曲线向内收敛，提高了隐身性能；同时，散射曲线分布规律不变，沿周向波峰分布规律一致，散射机理相似。

(2)频率影响规律：外形隐身措施对坦克模型具有较好的多频隐身效果，频率增加时，各角域RCS均值减小，前向H-60最低，同时各角域减缩值均呈增大趋势，隐身性能逐渐增强，前向H-60角域减缩值最高达26.771 3 dB。

(3)俯仰角影响规律：在-5～30°俯仰角范围内，前向H-60角域上，隐身模型RCS均值在-22.060 3～-18.608 3 dBsm，具有较好的隐身性能；减缩值在俯仰角0°最为明显，前向H-60角域可达24.473 4 dB，俯仰角增加时，各角域减缩值有一定降低。

(4)坦克电磁隐身性能影响：外形隐身技术明显降低前向、尾向及周向隐身性能，前向隐身性能最大可提高20 dB以上，在前向、后向和周向可同时实现多频、多俯仰角的隐身性能需求。