有学生 有数学 有技术
——《旋转》教学实践与思考
文|林志辉 陈柯柯
【教材内容】
人教版五年级下册第83、84页。
【教学设计】
活动一:三要素的认识
1.旋转中心。
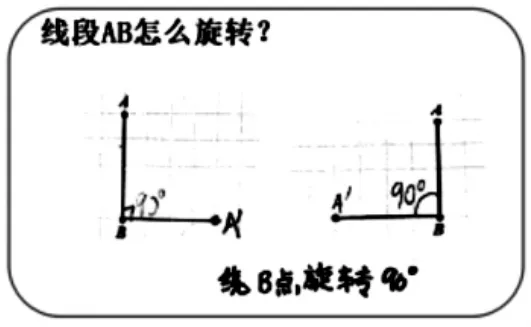
出示学生作品:

师:线段AB 是怎么旋转的呢?
生1:第一幅图顺时针旋转90°,第二幅图以A 点为中心,旋转90°。
生2:我要补充,第一幅图以B 点为中心,顺时针旋转90°,得到一个直角。
出示学生原有描述:

师:都是在旋转90°,怎么不一样呢?
生1:左边是绕B 点旋转90°,右边是绕A 点旋转90°。
生2:第一幅图是线段AB 绕着A 点旋转90°,第二幅图是线段AB 绕着B 点旋转90°。
师:像这样的点就是旋转中心。
基于学生素材,通过对比矛盾冲突,学生发现虽然都在旋转90°,但因为所绕着的旋转中心不一样,产生的旋转运动也是不一样的。
2.旋转方向。

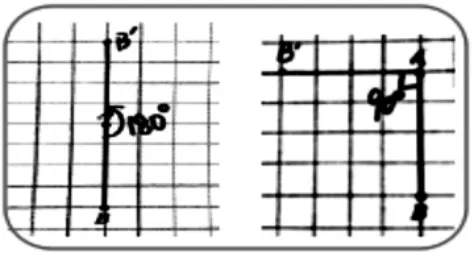
师:谁能说说现在线段AB是怎么旋转的?
生:线段绕着B 点旋转90°。
师:也是线段AB 绕着B 点旋转90°,怎么对应的A′点的位置不一样呢?
生:一个是顺时针,一个是逆时针。
师:还需要说明顺时针、逆时针,这叫做旋转方向。
【设计意图:旋转方向是旋转含义中的要素,通过学生素材的对比,学生发现想要准确地描述线段AB 的旋转还需要明确旋转方向。本环节除了利用二次矛盾冲突引出旋转方向外,更是对第一个环节旋转中心的巩固。】
3.旋转角度。
师:现在你能不能把课前对旋转的描述修改得更加准确呢?并和同桌说一说你的线段AB 是怎么旋转的。
展示学生作品:
(1)看图猜描述。

生:线段AB 绕A 点顺时针旋转90°。
(2)出示描述猜图。

师:你能想象他的线段AB 是怎么旋转的吗?对应的B′在哪里?
师:刚才这两幅作品都绕着A点旋转,怎么又不一样?
生:旋转角度不一样。

师:想象,O 点在哪里,对应的B′在哪里?

生:在线段AB 的中间,形状应是一个十字架。
师:现在让你继续描述线段AB 的旋转,你知道和哪些因素有关吗?
生:要有旋转中心、旋转方向和旋转角度。
4.小结。
师:仔细观察,线段AB 是怎么旋转的呢?(几何画板动态演示)
师:请想象,线段AB 绕着A点顺时针旋转270°,对应的点在哪里?用手势比划一下。
师:再想象,线段AB 绕着B点顺时针旋转90°,对应的点会在哪里?用你的手势表示出来。
【设计意图:基于学生的真实素材,通过不断地对比,学生逐步发现想要精准地描述旋转运动需要联系三要素。充分尊重学生知识的发生发展,学生通过修正、看图描述、看描述想象图,基于几何画板的应用,将直观表征和语言表征反复联系,巩固对旋转概念的理解,提升空间观念。】
活动二:旋转三角形ABC
师:想象,现在变成了三角形,三角形ABC 绕着B 点顺时针旋转90°,图会在哪里?对应的点在哪里?你有什么方法能画得又对又快呢?
学生活动,展示交流。

师:你赞同哪一幅作品?你是怎么想的?
生:第二幅作品,旋转图形其实和旋转线段是差不多的。先旋转线段BC。
师:太厉害了,不仅告诉我们怎么去检查,还交流了自己的画法。第二幅作品的学生画得很快,你猜猜他可能会有什么好方法?
生:先旋转一条线段绕着B点顺时针旋转90°,然后另一条也这么旋转,最后连接3 个点。
生:(画第二幅作品的学生)线段AB 顺时针绕着B 点旋转90°,然后线段BC 绕着B 点顺时针旋转90°,最后相连。
教师几何画板演示三角形的旋转过程。
【设计意图:图形的旋转归根结底是线段的旋转,在第一个三要素环节的基础上,学生自然而然地将三角形ABC 的旋转迁移到旋转中心为B 点,线段AB 和线段BC 的旋转上。学生通过对比操作表征,提炼操作的优化方法,将文字的表征和操作的表征进行联系,从而更深入地理解旋转的含义。】
活动三:旋转长方形ABCD
师:你们把图形的旋转看成了线段的旋转。加大难度———(课件演示变成长方形ABCD)
师:你想怎么旋转这个长方形ABCD 呢?旋转后对应的点会在哪里?你有什么方法可以画得又对又快呢?
学生活动,展示学生作品。
生:我创造了一个旋转,长方形ABCD 绕着B 点顺时针旋转180°。
师:想象一下会在哪里?
学生比划,教师出示学生作品。

师:你是怎么想象的?
生:先想象只有AB 绕着B点顺时针旋转180°,然后旋转线段BC,根据它们的画法确定D点,然后连接。
生1:长方形ABCD 绕着A点顺时针旋转90°。
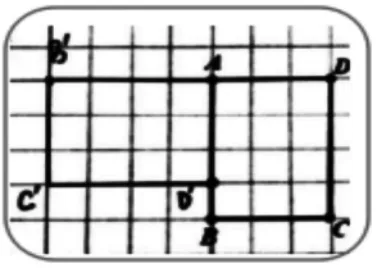
生2:长方形ABCD 绕着A点逆时针旋转270°。
【设计意图:创造性地旋转是考查学生对旋转含义的理解程度。学生要利用自己对旋转含义的理解,将脑海里的旋转操作表征出来,更要用语言表征出来,多种表征的互通直观呈现出学生的思维水平。创造贵在思维的新颖,学生在前面两个大环节的基础上,很容易固式地认为旋转中心大都为顶点,旋转角度大多为90°,这样的定格思维会扼杀学生的创造力和想象力,所以通过本环节让学生打破常规,开拓思维,将旋转的含义落实到位。】
师:如果绕着B 点顺时针旋转90°,想象会在哪里?如果再转下去呢?如果依次旋转下去呢?
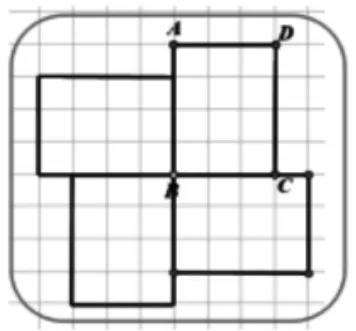
师:除了可以在B 点上,还可以在哪里?请想象,如果在A 点依次旋转下去呢?
师:还可以绕着哪个点旋转?如果逆时针旋转90°会怎样?再转下去呢?依次旋转下去呢?
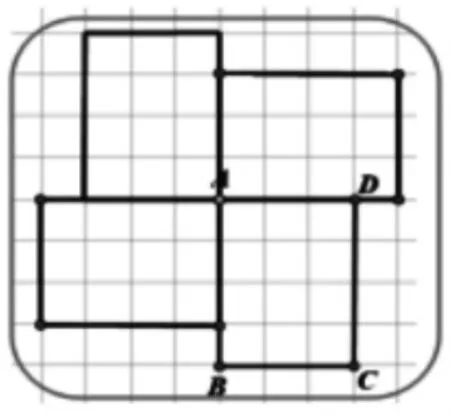
师:如果长方形ABCD 绕着D 点顺时针旋转30°,长方形ABCD 会在哪里?想象一下,依次旋转会在哪里?

师:还可以绕着哪个点?(几何画板演示,在中间、线段上、外面)

【设计意图:借助几何画板,丰富开阔学生的想象,将旋转中心移到线段中,将旋转中心移到长方形内、长方形外,将旋转的角度不断细分,让旋转依次出现,几何画板的呈现让学生打破固有思维,感受数学之美,感受极限之妙。】
【反思】
一、有学生——基于生本关注同化过程
本堂课所采取的课堂教学素材都来源于学生,从第一个环节的描述旋转,到第二个环节的刻画三角形旋转,再到第三个环节的创造长方形旋转,选取材料皆来自于学生。如第一个环节——描述旋转,从课前的调查,课中的对比反馈,学生在不断丰厚对旋转三要素的理解上对课前的文字表征又进行了修正,这是一个容错到融错再到改错的过程,充分关注到了学生对旋转含义的同化过程。学生在第二个环节刻画三角形旋转时,部分学生是有错误的,通过学生作品的对比优化改错,让学生完整经历图形的旋转归根于线段的旋转。最后通过学生创造长方形的旋转,为学生提供想象的平台,实时关注对知识的同化过程。
二、有数学——多元表征丰厚旋转概念
旋转是新课程增加的内容,具有较大的难度,具体表现在学生不能准确地刻画旋转,出现的错误各有不同,往往在这样的背景下,为了让学生掌握旋转,教师会采取高强度的技能性训练方法。学生画错真的只是因为技能操作不熟练吗?笔者通过大样本采集发现,究其原因是因为学生对于旋转定义三要素含义的落实不到位,即旋转中心、方向和角度,笔者本节课就是以深入理解旋转为导线开展旋转教学,不断将语言表征和动作表征互通,丰厚旋转含义,提升学生的空间观念。如旋转线段AB 中的文字与语言表征的互通,直观表征与语言表征的互通;旋转三角形ABC 时操作表征与文字表征的互通;旋转长方形ABCD 时语言表征和操作表征的互通,通过多元表征间的互通不断丰厚旋转含义。
三、有技术——几何画板彰显旋转本质
本节课还有一大亮点就是借助几何画板彰显旋转本质,突破想象瓶颈。线段AB 的旋转借助几何画板的实时互动功能,学生认识到了完整描述旋转必须具备旋转三要素。三角形ABC 的旋转借助几何画板,学生意识到图形的旋转就是某几条相关联线段的旋转。长方形ABCD 的旋转借助几何画板,突破了学生的创造瓶颈,将旋转中心、旋转角度和旋转方向通过依次不断变化、移动,让学生感受到数学的美。

