基于价值最优原则的综合能源供给系统分层优化配置策略研究

赵文强，余紫薇，赵建勇，雷国斌，徐嘉伟，张震霄，田 超，祁富志

(1.国网青海省电力公司电力科学研究院,青海 西宁 8100003；2.浙江省电机系统智能控制与变流技术重点实验室(浙江大学电气工程学院),浙江 杭州 310027；3.国网青海省电力公司果洛供电公司,青海 果洛州 814000)

0 引言

青海省许多农牧区域自然环境恶劣，居民居住分散，落实“户户通电”工程投资成本极高，因此，偏远地区农牧居民“用电难”、“用热难”问题亟需解决〔1〕。

针对偏远地区的供电问题，国内外一般通过建设微电网的方式来实现电力供应〔2〕。针对偏远地区的供热问题，通常考虑在原有微网的基础上，实现“热电联供”〔3-4〕。热电联供技术具有节能、高效、能源利用率高等优点，可以同时为用户提供电力、热力等多种能量，并能够就地消纳太阳能等清洁能源，实现能源的环保经济利用，广受电力系统的欢迎。文献〔5〕结合了太阳能光伏发电、储能、地源热泵构成了一体化微网系统，多种能量形式的互存有效提高了能源利用效率。

青海省具有显著的光资源和土地资源优势，因此建立以光伏发电为主，综合利用分布式发电、储能、储热的先进技术的光、储、热一体化的新型能源供给系统，成为解决青海省偏远地区供电供热难题的一条有效途径。为保证该新型能源供给系统的安全运行，并满足供电供热的稳定性需求，需要对系统组成进行合理容量配置。但现有针对微网系统的优化配置方法，通常以运行成本或能源利用率为优化目标，一般只涉及到电力供配的情况。文献〔6〕提出了一种基于文化基因算法的交直流混合微网优化运行方法，该方法有效降低了微网系统的运行成本，并保证了交直流不同负荷的稳定供电，但该方法并不适用于电力、热力同时存在的系统工况。

对此，本文提出了一种光、储、热新型能源供给系统分层优化配置方法，以保证该新型能源供给系统的经济稳定运行。

1 光、储、热新型能源供给系统结构

本文重点对分布式发电、储能、储热等部分，进行合理的容量配置。为简化分析，并保证足够的成本预测精度，图1给出了新型能源供给系统的结构示意图。如图1所示，新型能源供给系统可以分成电力系统层和热力系统层。其中，光伏发电单元、储电单元、变流器单元构成了电力系统层，用于电负荷的供电；而电热转换单元、储热单元构成了热力系统层，用于热负荷的供热，而电热转换单元直接由光伏发电单元提供电量。

2 基于价值最优原则的新型能源供给系统优化配置模型

针对图1系统结构图，本节提出了基于价值最优原则的新型能源供给系统优化配置模型，求解系统容量的最优配置方案，从而实现系统的经济运行，并满足偏远地区供电供热的稳定性需求。

2.1 表征系统容量配置的经济性目标函数

首先，建立了表征系统容量配置的经济性目标函数。该目标函数由以下各成本组成：

(1) 系统各单元的投资成本

光、储、热新型能源供给系统包含光伏发电单元、储电单元、储热单元、变流器单元和电热转换单元，同时实现电力热力的稳定供应。系统中各单元的的投资成本可统一由下式表示：

Ccon(i)-Cres(i))

(1)

式中，N(i，j)为第j次优化配置过程中第i类系统基本单元的配置数量;Cini(i)、Csetup(i)、Ccon(i)、Cres(i)分为别第i类系统基本单元单位化的初始投资、安装、配套变换器费用和剩余成本。

(2) 光伏发电单元的运行维护费用

(2)

式中，KPV为光伏发电单元的维护成本系数，PPV(t)为t时刻光伏发电单元所发出的功率。

(3) 储电单元的维护费用

考虑到储电装置的性能及对电力供应的稳定性要求，通常选用以蓄电池为基础的储电单元。只考虑蓄电池的储电单元维护费用为

(3)

式中，Kbat为蓄电池单元的维护成本系数，Pbat(t)为t时刻蓄电池单元所发出或吸收的功率。

(4) 储热单元的运行维护费用

(4)

式中，Ksto为储热单元的维护成本系数，Psto(t)为t时刻储热单元所发出或吸收的功率。

(5) 变流器单元的运行维护费用

(5)

式中，Kinverter为变流器单元的维护成本系数，Pinverter(t)为t时刻变流器单元发出的功率。

(6) 电热转换单元的运行维护费用

(6)

式中，KEtT为电热转换单元的维护成本系数，PEtT(t)为t时刻电热转换单元发出的功率。

2.2 满足供电供热稳定需求的约束条件

其次，为实现新型能源供给系统的合理运行，并满足偏远地区供电供热的稳定需求，建立相应的约束条件如下：

(1)系统功率平衡约束

新型能源供给系统采用光伏作为可再生能源发电单元，供给系统内电热负荷能量需求。在此基础上，系统功率平衡约束条件可用如下公式表示：

PELoad(t)+PTLoad(t)=PPV(t)+Pbat(t)+Psto(t)

(7)

式中，PELoad(t)、PTLoad(t)为t时刻电、热负荷消耗功率，PPV(t)为t时刻光伏发电单元产生功率，Pbat(t)、Psto(t)为t时刻储电、储热单元吸收或释放功率。其中，光伏发电单元输出功率PPV(t)与当前环境温度、光照强度和当前风速有关，可由如下公式计算：

(8)

式中，PN为光伏组件在标准测试环境下的额定出力，fd为光伏组件的衰减系数，G(t)为第t时刻光伏组件上的平均入射太阳辐照度，Gref为标准测试条件下的辐照度，Tcref为标准测试条件下的温度，αT为温度影响系数。

(2)储电单元的容量和功率交换能力约束

储电单元存在容量上的限制，因此t时刻储电的荷电状态(SOC)需满足：

SOCmin≤SOC(t)≤SOCmax

(9)

式中，SOCmin为最小荷电电量，SOCmax为最大荷电电量。

同时，储电单元存在单位时间内吸收或释放功率限制：

0≤Pbat(t)≤Pbat_max

(10)

式中，Pbat_max为储电单元的最大吸收或释放功率，其受到变流器单元额定功率的Pinverter限制。

(3) 储热单元的容量和功率交换能力约束

储热单元存在容量上的限制，即t时刻储热装置储热量Q(t)不超过最大储热容量Qmax：

0≤Q(t)≤Qmax

(11)

同时，t时刻储热单元吸收或发出功率Psto(t)受换热器换热功率的限制：

(12)

式中，Hin_max为储热单元的最大吸热功率，Hout_max为储热单元的最大放热功率。

(4) 储电单元的效率约束

储电单元需要考虑到能量传递、转换过程中的效率问题。假设储电单元的充放电效率在运行过程中保持不变。对于储电单元，计及充电效率和放电效率后SOC离散形式可如下式表示：

SOC(t)=SOC(t-1)+α·Pbat(t)Δt

(13)

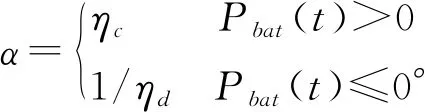
(5)储热单元的效率约束

储热单元需要考虑到能量传递、转换过程中的效率问题。对于储热单元，t时刻吸收的热量是由电热转换单元提供，假设电转化为热的转化效率为ηet，则：

Psto(t)=ηetPin(t)

(14)

式中，Pin(t)为电热转换单元的输出功率。

假设储热单元与热负荷间功率传递的效率为ηeo，则：

Pout(t)=1/ηeo·Psto(t)

(15)

式中，Pout(t)为储热单元给热负荷供热的实际输出功率。

(6)负载失电率约束

在满足系统功率平衡条件的基础上，负载失电率将作为新型能源供给系统全年运行的供电可靠性指标，从而实现系统满足负载失电率要求下的容量配置。系统运行过程中的负载失电量可如下式所示：

PLPS(t)=PELoad(t)-PPV(t)-Pbat(t)

(16)

在正常供电情况下，负载失电量PLPS(t)=0。定义负载失电率为系统运行过程中负载累积失电量与负载消耗总电量之比，可得：

(17)

(7) 热量缺损率约束

在满足系统功率平衡条件的基础上，热量缺损率将作为新型能源供给系统全年运行的供热可靠性指标，从而实现系统满足热量缺损率要求下的容量配置。系统运行过程中的热量缺损可如下式所示：

PTPS(t)=PTLoad(t)-PPV(t)-Psto(t)

(18)

在正常供热情况下，热量缺损率PTPS(t) = 0。定义热量缺损率为系统运行过程中热负荷累积缺损供热量与热负荷总需供热量之比，可得：

(19)

2.3 基于价值最优原则的优化配置模型

根据已有的经济性目标函数和约束条件，可建立基于价值最优原则的新型能源供给系统优化配置模型如下：

(20)

式中，f1(X1，j)，f2(X2，j)分别表示系统的年化投资费用和运行维护费用。h1(X1，j)、g1(X1，j)等表示系统的约束条件，S1等为系统变量的可能范围。其中，f1(X1，j)，f2(X2，j)分别表示为：

(21)

(22)

3 分层优化迭代算法

基于上述建立的优化配置模型，本文采用分层优化迭代算法，用于求解系统价值最优的容量配置结果。所采用的分层优化迭代算法步骤如下：

(1) 步骤一：数值初始化

已知目标地区典型m天1-24 h各时刻的电负荷数据PEload(t)和热负荷数据PTload(t)；根据目标地区的地理、温度、太阳辐射率等环境参数，由式(8)计算得到目标地区m天1-24 h各时刻单位光伏单元的输出功率PPV_one(t)；由PPV_one(t)、PEload(t)、PTload(t)，初步确定光伏发电单元功率、储电单元容量、储热单元容量、变流器单元功率和电热转换单元功率的最大可执行范围。

(2) 步骤二：条件假设

假设一：m天初始时刻，储电单元的初始荷电状态最低，储热单元的初始储热量为0，即

SOC(0)=SOCmin
Q(0)=0

(23)

假设二：考虑到储热单元的成本明显低于储电单元，为最大化储热单元的功能作用，降低系统的经济性成本，假设新型能源供给系统中热力子系统所需热量是由光伏发电单元产生后，直接经电热转换单元转换至热力子系统，而不由储电单元供给，即新型能源供给系统的电力系统层和热力系统层可分别进行迭代操作，完成各自的优化配置。

(3) 步骤三：电力系统层的迭代操作

针对某一组电力系统层的容量配置(PPVE,Pinverter,SOCmax)，进行电力子系统迭代操作如下。其中，PPVE为光伏单元总额定功率，Pinverter为变流器单元总额定功率，SOCmax为储电单元总额定容量。

①当t时刻PPV(t)>PEload(t)时, 判断储电单元电量SOC(t)是否小于储电单元总额定容量；若判断成立，则确定充电功率大小如下，并根据式(13)完成储电单元的充电操作。

(24)

式中，Pinverter与充放电功率的最大功率近似Pbat_max相等，从而满足储电单元功率交换能力约束。 若储电单元电量SOC(t)大于或等于SOCmax，则不进行充电操作，并令SOC(t)=SOCmax。

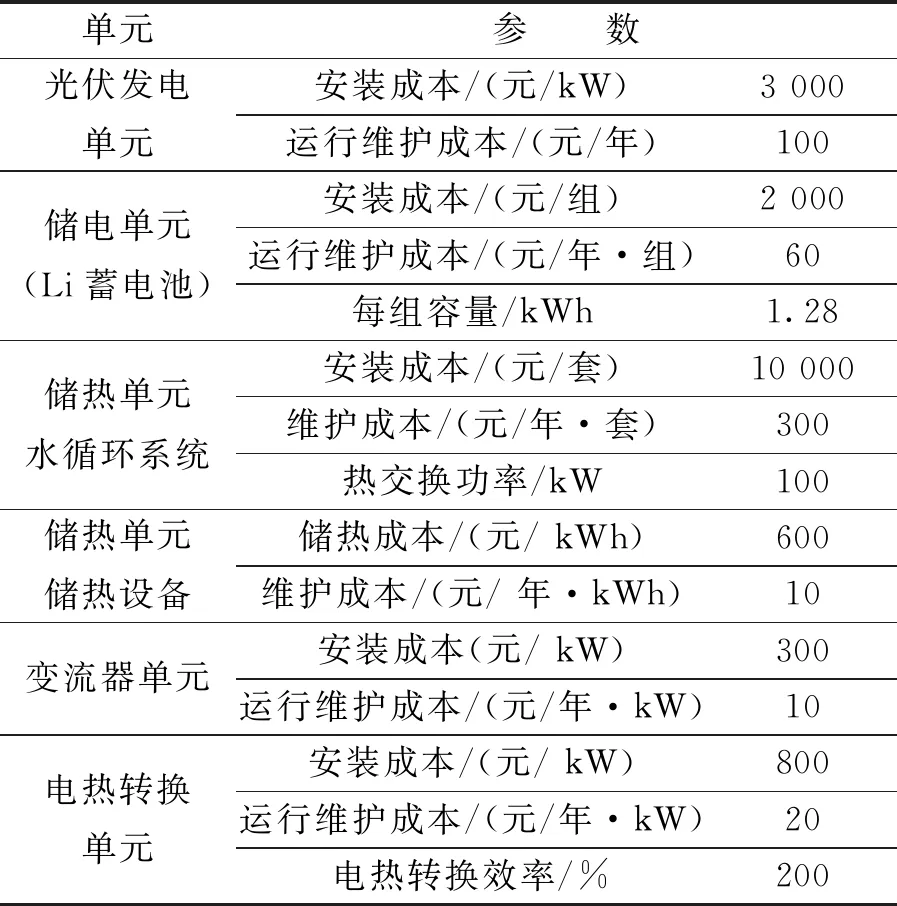
②当t时刻PPV(t)

(25)

③依次求得m天1-24 h各时刻储电单元的电量SOC(t)，并计算各时刻的负载失电率PLPS(t)：

(26)

④在电力系统层的最大执行范围内，按照设定步长，改变电力系统层的容量配置，并重新进行上述的迭代操作。其中，步长由电力系统层包含的各单元单位功率或容量决定。

(4)步骤四：热力系统层的迭代操作

针对某一组热力子系统容量配置情况(PPVT,Qmax)，进行热力系统层迭代操作如下。其中，PPVT为光伏单元总额定总功率，Qmax为储热单元总额定容量，电热转换单元总额定功率直接由PPVT和电热转换能效比决定。

①当t时刻，光伏发电单元经电热转换单元的输出功率PPV_T(t)>PTload(t), 判断储热单元热量Q(t)是否小于储热单元总容量Qmax；若判断成立，则储热单元吸收热量，由式(14)确定储热单元的吸热功率为Psto(t)。若判断不成立，则不进行储热操作，并令Q(t)=Qmax。

②当t时刻PPV_T(t)

③依次求得m天1-24h各时刻储热单元的热量Q(t)，并计算各时刻的热量缺损值PTPS(t)如下：

(27)

④在热力系统层的最大执行范围内，按照设定步长，改变热力系统层的容量配置，并重新进行上述迭代操作。其中，步长由热力系统层包含的各单元单位功率或容量决定。

(5) 步骤五：负载失电率及热量缺失率评价

①根据负载失电率的约束条件，判断各组电力系统层的容量配置方案，确定满足负载失电率约束条件的电力系统层各容量配置方案。

②根据热量缺损率的约束条件，判断各组热力系统层的容量配置方案，确定满足热量缺损率约束条件的热力系统层各容量配置方案。

(6) 步骤六：价值最优方案的选取

计算步骤五得到的电力、热力系统层各容量配置方案经济性成本，搜索价值最优的电力、热力系统层配置方案；

综合上述价值最优的电力、热力系统层配置方案，得到基于价值最优原则下光、储、热新型能源供给系统价值优化配置结果。

4 算例分析

为了验证上述所提出的优化配置方法，本文根据某偏远地区的电负荷、热负荷、单位光伏单元发力数据，设计对应的容量配置方案，并进行了算例分析。算例中，新型能源供给系统结构如图1所示，其中，储电单元采用Li蓄电池，电热转换单元采用量子电锅炉，能效转换比为2，储热单元需配备水循环单元来完成吸收、释放热量。

图2给出了某偏远地区典型7天电负荷、热负荷和单位光伏发电单元出力的预测变化曲线。其中，电负荷最大功率为746 kW，热负荷最大功率为1 124.2 kW。表1给出了新型能源供给系统各单元的成本参数。

表1 新型能源供给系统各单元成本

根据图2中电负荷和单位光伏发电单元出力的预测数据，设定负载失电率的约束条件为第六天全天负载累计失电量小于74.6 kW(当天最大电负荷功率的10%)，使用期限10年。采用双层优化迭代算法，电力系统层第六天累计负载失电量迭代曲线如图3所示。经价值最优选择，得到电力系统层最优配置结果为：光伏发电单元1.3 MW，变流器单元0.2 MW，储电单元409组，总成本634.34 万元。图4为该电力系统层最优容量配置下各单元的功率(容量)曲线。由图可知，在此电力系统层最优配置下，能源供给系统的负载失电量极低，能够很好地满足偏远地区的供电稳定性需求。

根据图2中热负荷和单位光伏发电单元出力的预测数据，设定热量缺损量的约束条件为第六天全天累计热量缺损量小于112.42 kW(当天最大热负荷功率的10%)，使用期限10年。采用双层优化迭代算法，热力系统层第六天累计热损量迭代曲线如图5所示。经价值最优选择，得到热力系统层最优配置结果为：光伏发电单元1.3 MW，电热转换单元1.3 MW，储热单元水循环系统13套，储热单元10 MWh，总成本1 366.9 万元。图6为该热力系统层最优容量配置下各单元功率(容量)曲线。由图可知，在此热力系统层最优配置下，能源供给系统的热损量极低，能够很好地满足偏远地区的供热稳定性需求。

由此确定光、储、热新型能源供给系统价值最优的容量配置方案如下：光伏发电单元2.6 MW，电热转换单元1.3 MW，储电单元409组，储热单元水循环系统13套，储热单元10 MWh，变流器单元0.2 MW，总成本2 001.2万元。图7给出了新型能源供给系统最优容量配置的成本分布。

5 结论

本文提出了一种基于价值最优原则的光、储、热新型能源供给系统分层优化配置方法，能够保证偏远地区电力热力的稳定需求，并有利于新型能源供给系统的经济运行。本文根据表征系统容量配置的经济性目标和满足供电供热稳定需求的约束条件，建立了相应的系统优化配置模型，并提出了相应的分层优化迭代算法，用于求解价值最优的系统容量配置结果。最后，由给出案例分析，有效验证了所提出的分层优化方法的可行性。