云制造服务综合评价方法研究

张理志，苑明海*，周开俊，李亚东

(1.河海大学 机电工程学院，江苏 常州 213000；2.南通河海大学 海洋与近海工程研究院，江苏 南通 226300；3.南通职业大学，江苏 南通 226300)

0 引 言

随着云制造模式的推进，云制造服务的评价理论方法也不断更新，云制造服务的评价对于整个云制造平台的运行有着关键作用，为整个云制造系统中制造资源的调度提供了基础性保证。陈友玲等[1]提出了从企业维、服务维、交互维三个方面建立服务能力评价体系，利用变精度粗糙集算法计算权重值及敏感系数修正用户偏好的方法进行求解服务能力值。封宇等[2]提出了一种层次化可配置的可信评价模型，将评价对象分为服务实例、服务产品、服务主体三个层次。胡艳娟等[3]基于模糊理论，采用定量与定性相结合，建立综合评价指标体系和综合评价模型。贺可太等[4]建立了一般评价指标体系和可扩展的量化模型，用项目协同的方法校正指标数值，利用三角模糊数算法计算相似度，得到服务质量综合性能排序，快速优选出最佳服务。王泽[5]利用熵值法为各属性项目进行比重取值，将资源进行模块化切入形式，对QoS评价模型进行改进。谢灿等[6]提出采用G1-法和变精度粗糙集理论两种赋权方法对云制造服务进行评价。Zhao等[7]提出了基于预测评估和推荐评估的资源选择方法；Huang等[8]提出了一种用于云制造服务的自组织评价方法，并在此基础上提出了一种结合熵值法的云制造服务自组织评价算法。Zhang等[9]提出了一种基于订单偏好与理想解决方案相似度的面向客户的评估方法，以及一种实时订单分配机制。Feng等[10]提出了一种基于协作过滤的可配置信誉评估方法。Khamdi等[11]提出了一种分层的可靠性评估模型来评估云制造服务的可靠性。Yang等[12]通过对历史服务评估数据进行量化，提出了基于服务满意度的信任评估模型。唐娟等[13]提出了基于可信评价的基于DS/AHP的云制造服务质量评价方法。

1 云制造服务综合评价建模

1.1 模糊综合评价算法

模糊理论是指用到了模糊集合的基本概念或连续隶属度函数的理论，是由美国加州大学教授L.A.Zadeh提出[14]。该文主要根据模糊理论中的模糊数学与模糊决策两部分，充分考虑和接受评价对象的意见，并且全面地做好面对多种情况同时发生的准备。当前的云制造服务评价体系中，评价指标多种多样，具有明显的层次化特征，与云制造服务特点相匹配，根据模糊数学，建立模糊综合评价模型。

当评价对象比较复杂，影响因素较多时，可根据模糊综合评价算法，进行一级评价和多级评价，但一级评价不足以体现多层次模糊综合评价的优势。同时，由于评价指标要进行权重归一化处理，但会使各指标权重相对较小，差距较小，因此很难分配权重，且可能造成结果不准确。在此基础上，首先对低级评价指标进行综合评价，得出的结果作为高一级评价的参考值，这样逐层评价，形成完整的综合评价结果。图1所示为云制造服务的多层次模糊综合评价模型的流程。

图1 多层次模糊综合评价模型的流程

云制造服务综合评价的指标体系多样复杂，为使各评价指标的重要程度均有体现，使各评价指标达到最优，且加权平均型算子具有体现权重作用明显、模糊关系矩阵利用程度充分、综合程度强等特点，因此综合考虑，选择加权平均型模糊算子[15]。

将云制造服务综合评价指标体系中每个指标的综合权重与每级评价的模糊关系矩阵R按加权平均型模糊算子进行运算，即可得到每级被评价指标的模糊综合评价结果向量F：

(1)

1.2 层次分析法与熵权法组合权重

1.2.1 层次分析法确定权重

层次分析法由目标层、准则层及对象层组成，用求解判断矩阵特征向量的方法，解得每一层次的各元素对上一层次某元素的优先权重，再根据加权和的方法计算得出总目标权重，即可对评价对象进行评价[16]。

层次分析法建模过程：第一、确定评价对象，建立各层次评价模型；第二、构造判断矩阵；第三、进行层次单排序；第四、进行层次总排序，具体如下：

首先，通过对评价对象的详细研究分析后，建立适当的评价结构模型，通过层次化模型将复杂问题简单化，一般分为三个层次，即最高层、中间层、最底层，上层因素对下层因素起支配作用。

其次，构造判断矩阵，层次化结构模型建立好，确定了不同层次之间的逻辑关系。为了确定同一层次中各因素的比重，引入两两对比判断矩阵，即1-9标度成对比较矩阵，如表1所示。构造m阶两两对比判断矩阵，其中B=(bij)m×m代表同一层次所有两两对比因素组成的矩阵，m是因素的个数，bij是xi和xi相对于上一层次中某元素的重要程度的比值，bij是bji的倒数。

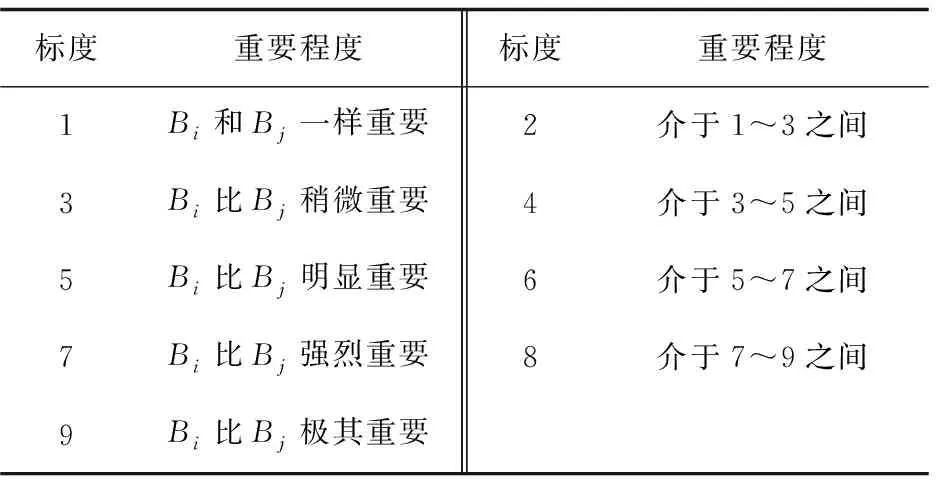
表1 1-9标度

再次，根据判断矩阵B，由公式BW=λmaxW可知λmax为B的最大特征根，求解最大特征根的具体步骤如下：

(1)对B中元素进行归一化处理：

(2)

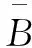
(3)

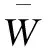
(4)

由上可得因素权重的大小，但还需进行一致性检验。由判断矩阵B=(bij)m×m计算得出wi，得出：

(5)

将得出的最大特征值代入下式，可得出一致性指标值CI。

(6)

查找相对应的平均随机一致性指标，如表2所示。

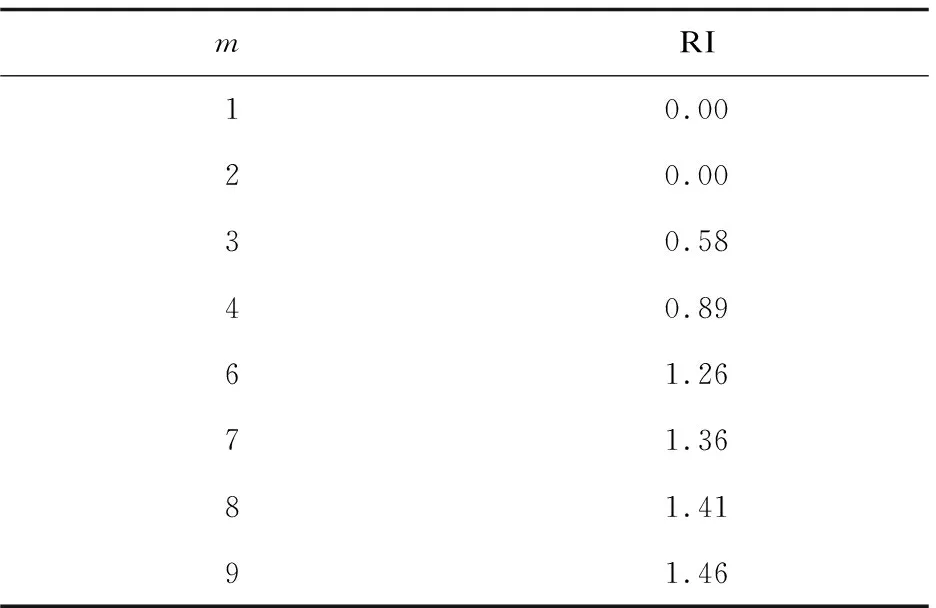
表2 平均随机一致性指标

再根据下式得出一致性比值CR。

CR=CI/RI

(7)

当CR<0.1时，则两两对比判断矩阵符合，否则需进一步修正判断矩阵。

以上得出的是一组元素与其对应的上一层某个元素的权重，由上至下逐层计算，可得同一层次所有元素相对于最高层元素权重的总排序，由表3计算出层次总排序权重。

表3 层次排序

若已知E层次的单排序一致性指标CI(j),j=1,2,…,m以及平均随机一致性指标RI(j)，则F层次总排序一致性检验为：

(8)

同理，当CR<0.1时，权重合理可采用。

1.2.2 熵权法确定权重

熵是系统无序程度的一种度量，若指标的信息熵越小，则该指标提供的信息量越大，在综合评价中作用越大，权重越高。因此，利用熵权法计算各指标的权重，为综合评价提供依据。

熵权法是一种客观的赋权方法，具体的建模步骤如下：在云制造服务综合评价指标体系中，设有m个云制造服务样本，每个样本中包含n个评价指标，其相对应的各指标值为bij(i=1,2,…,m;j=1,2,…,n)，其指标矩阵为B=(bij)m×n。

首先对样本指标矩阵进行归一化处理，分为越大越优型指标和越小越优型指标，处理公式分别如下：

(9)

(10)

矩阵标准化之后，则第i个指标的熵值ei为：

(11)

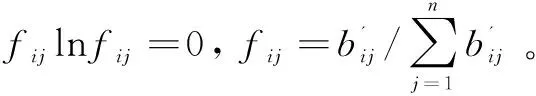
当得出第i个指标的熵值后，则第i个熵权为：

(12)

即熵权法得出的评价指标权重为βi。

1.2.3 综合权重确定

第一级评价指标用层次分析法确定，第二级评价指标的权重由层次分析法与熵权法共同确定，得到综合权重，如下式：

αi=δwi+(1-δ)βi

(13)

其中，δ为主观偏好系数，1-δ为客观偏好系数，该文认为主客观偏好同等重要，因此取δ=0.5。

2 云制造服务综合评价指标体系

2.1 评价指标体系的构建原则

智慧云制造环境下，云制造服务受多方面因素影响，为了得到科学、准确的评价结果，应建立合理、科学、全面的云制造服务评价指标体系[17]。建立体系需遵循下列准则：

(1)全面性原则。

为了能够对云制造进行全面、完整、系统的评价，在构建评价指标体系时应遵循全面性原则。

(2)准确性原则。

云制造服务评价指标体系应该以准确性原则为基础，能够真实、客观地反映云制造服务水平，各评价指标的概念准确、清晰、独立。

(3)适用性原则。

进行云制造服务综合评价时，为了使云制造服务评价指标体系能够在实际应用中起到评价和指导的作用，该评价指标体系必须具有适用性。

(4)简便性原则。

在选择云制造服务评价的指标时，应该充分考虑云制造服务评价体系的简洁性。如若评价指标的数量不仅多且复杂交叉，则会使评价结果不准确。

2.2 评价指标的确定

云制造服务是一个复杂的服务组合系统，建立完善的云制造服务评价指标体系需要选择准确、全面的评价指标。根据上述构建原则，该文建立的云制造服务资源的综合评价体系中，包含七个一级指标及十六个二级指标。一级指标为：时间、成本、质量、服务、信誉度、柔性、可靠性。

(1)时间指标，指云制造服务平台接收到任务需求所需要的响应时间、在加工过程中需要的时间、物流运输搬送的时间，时间指标可直接反映出资源的好坏。

(2)成本指标，指整个产品的加工成本、物流花费、软件资源的升级维护费用等。

(3)质量指标，主要指技术质量及产品合格率。

(4)服务指标，指云制造服务资源的可使用性和服务能力。

(5)信誉度指标，指云制造服务的完成效果及服务的准时性和及时性。

(6)柔性指标，指云制造服务资源在面对非确定因素时的应变能力。

(7)可靠性指标，指能按时完成任务和高质量完成任务的能力。

2.3 多层次云制造服务评价因素集

由上述内容可知，云制造服务综合评价指标体系是一个二级体系，可知每个一级指标(质量指标Q1、成本指标C1、时间指标T1、服务指标S1、信誉度指标B1、柔性指标F1、可靠性指标D1)都可构成一个模糊评价的过程。因此，评价过程即为先对每一个一级指标对应的二级指标进行评价，再最终对一级指标进行评价，逐层评价之后得出综合评价结果。

第一层评价因素集为:

第二层评价因素集为：

2.4 构建云制造服务评价对象评语集

由上述云制造服务综合评价指标体系可知，第二级评价指标类型多样，其指标的取值范围波动较大，因此需建立不同指标的评语集。

该文将评价指标的评语集定为“优秀、良好、中等、及格、不及格”五个等级。在十六个二级指标之中有四个指标为定性指标，设置与五个等级相对应的值为95、85、75、65、55(单位均为：%)。定量指标有十二个，具体的等级对应值如表4所示。

表4 指标评语集

2.5 建立多层次云制造服务综合评价指标模糊关系矩阵

由上述表中内容，对评价指标进行模糊处理，再对每个评价指标从各因素上进行量化处理，从而根据单因素得出被评价指标与所对应的等级模糊子集的隶属度。该文利用模糊梯形分布及三角函数分布，计算各评价指标的隶属度。由于评价指标有两种类型，越大越优型和越小越优型，不同类型采用的指标公式不同，具体如下：

(1)越大越优型(模糊升梯形公式)。

(14)

(15)

(16)

(2)越小越优型(模糊降梯形公式)。

(17)

(18)

(19)

其中，i=2，3，4，r1，r2，r3，r4，r5表示经过模糊运算后对应于五个等级的隶属度值，k1，k2，k3，k4，k5分别对应“优秀、良好、中等、及格、不及格”五个等级，x表示不同评价因素集对应于指标的实际值。

(20)

3 实例验证

3.1 计算模糊矩阵

为了证明该文云制造服务综合评价模型的可适用性及简便操作性，以一个云制造服务为例，计算操作过程，得出评价结果，表5为该云制造服务各评价指标的实际值。

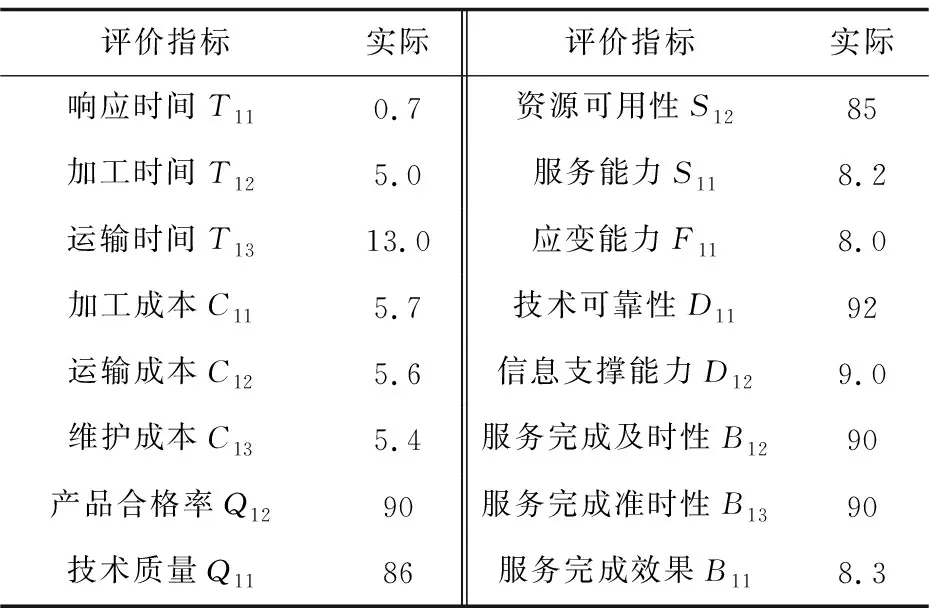
表5 评价指标实际值

下面以计算时间指标为例，且时间指标为越小越优型指标，代入公式，可得出时间指标的隶属度子集为：

即可得到服务时间指标的模糊评价矩阵为：

同理可得：

成本指标的模糊评价矩阵为：

质量指标的模糊评价矩阵为：

服务指标的模糊评价矩阵为：

信誉度指标的模糊评价矩阵为：

柔性指标的模糊评价矩阵为：

可靠性指标的模糊评价矩阵为：

3.2 确定权重

(1)层次分析法计算主观权重。

(i)根据表1构造两两对比判断矩阵，如表6所示。

表6 判断矩阵

(ii)层次单排序。

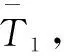
(iii)一致性检验。

同理，可计算得出其他指标权重，利用上述一致性检验公式检验各权重合理性，检验结果均合理。

(2)根据熵权法计算客观权重。

利用上述熵权法求解权重公式，利用Matlab软件编程可得出各指标的实际权重，一共十六个二级指标，如表7所示。

表7 熵权法求解权重值

(3)求出组合权重。

根据式(8)，可计算得出：

3.3 多层次模糊综合评价

由式(1)可分别计算二级评价指标的模糊评价结果矩阵和一级评价指标的模糊评价结果矩阵，具体结果如下：

FT=αT*RT1=

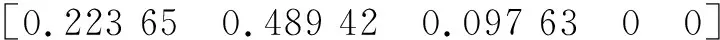
FC=αC*RC1=

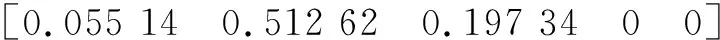
FQ=αQ*RQ1=

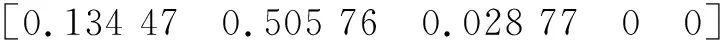
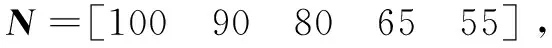
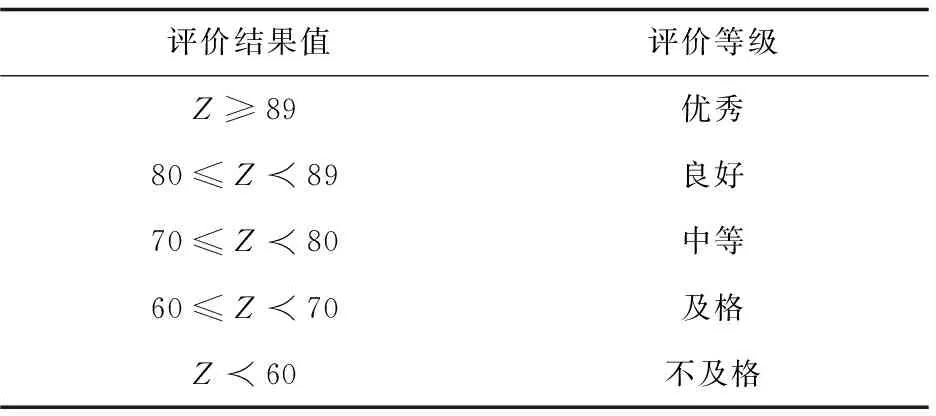
表8 评价等级

根据评价等级表8，可知该云制造服务属于优秀等级。

4 结束语

首先根据当前的云制造服务评价体系中评价指标多种多样，具有明显的层次化特征，与云制造服务特点相匹配，根据模糊数学，建立模糊综合评价模型，并确定了由层次分析法和熵权法组合确定权重的方法。其次确定了一级和二级评价指标，建立了云制造服务资源综合评价指标体系。最后，通过云制造服务实例验证了该模型及方法的操作简便性及实用性。