基于Workbench 板簧支架轻量化设计

王海波

（200093 上海市 上海理工大学）

0 引言

汽车作为现代工业化的标志性产业，是能源消耗的主要产品。汽车行业的发展必须要具备新的技术、材料和先进制造工艺，以降低汽车消耗，缓解能源危机。根据资料显示，减低汽车的质量是降低能耗的一个有效措施[1]。

本文以板簧支架为研究对象，首先对初始模型进行静力学分析，然后分别以安装板厚度T1,大筋板厚度T2，小筋板厚度T3 为设计变量，进行尺寸优化，求出满足强度厚度的最优解。以求出的最优解建立新的模型，进行拓扑优化设计。以拓扑优化后的模型为参考对象进行轻量化设计，分别以切除深度H 和切除三角形边长L 为设计变量，进行结构优化，求出在满足强度条件下H 和L 的最优解，为板簧支架的轻量化设计提供参考。

1 板簧支架的初始模型建立与分析

1.1 板簧支架初始模型的建立

本文利用SolidWorks 对板簧支架进行建模，如图1 所示，对于一些细微特征予以忽略，如：倒角、小孔等，并将安装板厚度T1,大筋板厚度T2，小筋板厚度T3进行参数化处理，初始模型的质量为11.5 kg。

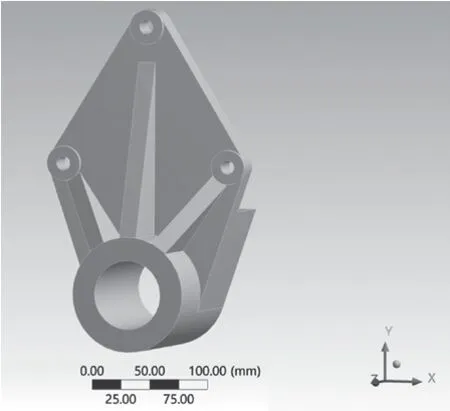
图1 板簧支架三维模型Fig.1 Three-dimensional model of leaf spring bracket

2.2 静力学分析

将建立好的板簧支架三维模型导入Workbench 中，选取Static Structural 模块，进行相关参数的设置。设置材料为Structural Steel，密度为7 580 kg/m3，弹性模量为200 GPa，泊松比为0.3，屈服强度为250 MPa；单元大小设置为6 mm，相关系数调整为100%。对3 个螺纹孔施加固定约束，在板簧支架连接孔中施加X，Y，Z三个大小为10 000 N 的力[3]。分析后板簧的总变形云图如图2 所示，等效应力云图如图3 所示。最大变形为0.18 mm，最大等效应力为183.88 MPa，满足使用要求。

图2 板簧支架总变形云图Fig.2 Overall deformation cloud diagram of leaf spring bracket

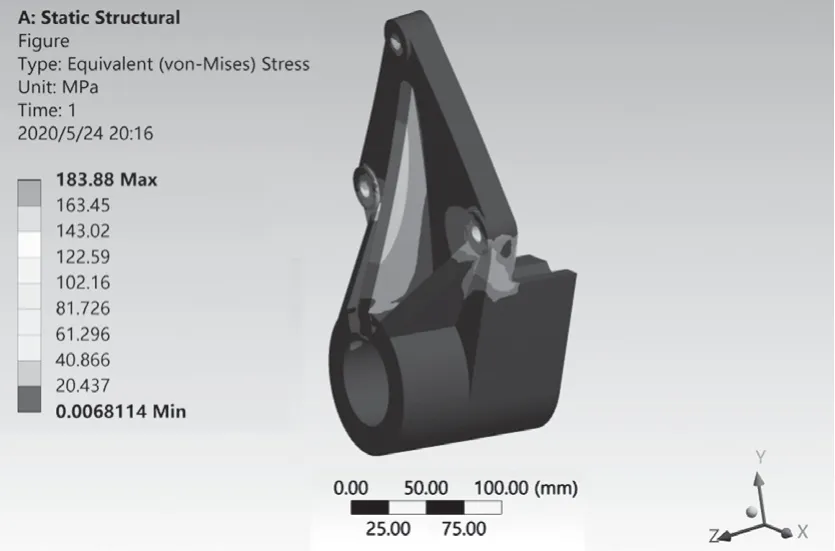
图3 板簧支架等效应力云图Fig.3 Equivalent stress cloud diagram of leaf spring bracket

2 板簧支架多目标尺寸优化

多目标尺寸优化的目的是减轻板簧支架的质量[2,4]，以Workbench 中的Static Structural 模块和Response surface 模块进行联合仿真，求出在满足使用要求条件下的最优解。

2.1 设计变量的选择

根据对板簧支架模型质量、强度以及刚度影响因素的分析，设定板簧支架模型的设计变量，设计变量有：安装板厚度T1,大筋板厚度T2，小筋板厚度T3。对设计变量进行参数化处理。

DS_ T1：安装板厚度；DS_T2：大筋板厚度；

DS_T3:：小筋板厚度。

设计变量的变化范围表1 所示。

表1 设计变量的变化范围Tab.1 Design variable range

2.2 目标函数的设置

目标输出函数为最大等效应力、最大总应变及质量[2,4]，将其进行参数化设置，并为其设置约束条件。

P4-质量（Geometry Mass）=最小值（Minimize）；P5-总 应 变（Deformation Maximum）≤1 mm；P6-最大等效应力（Equivalent stress Maximum）≤190 MPa。

2.3 优化结果分析

系统根据优化目标及约束条件将设计变量组合为15 个设计点，并在其中找出最优设计点4，如图4 所示。

图4 设计点分布Fig.4 Design points distribution

优化后的取值，P1-T1=21 mm，P3-T2=16 mm，P2-T3=12 mm。将参数带入原模型进行静力学分析，得到模型的质量为11.5 kg，最大总变形为0.16 mm，最大应力为156.13 MPa。总变形云图和等效应力云图如图5、图6 所示。大筋板厚度P3-T2及小筋板厚度P2-T3对最大等效应力的影响如图7、图8 所示。

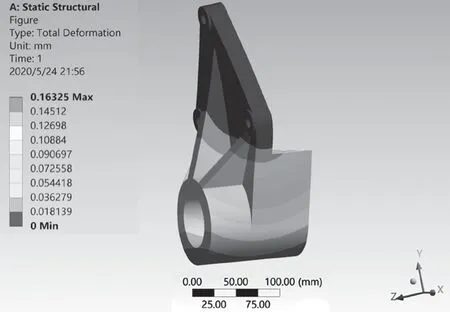
图5 尺寸优化后总变形云图Fig.5 Overall deformation cloud after size optimization

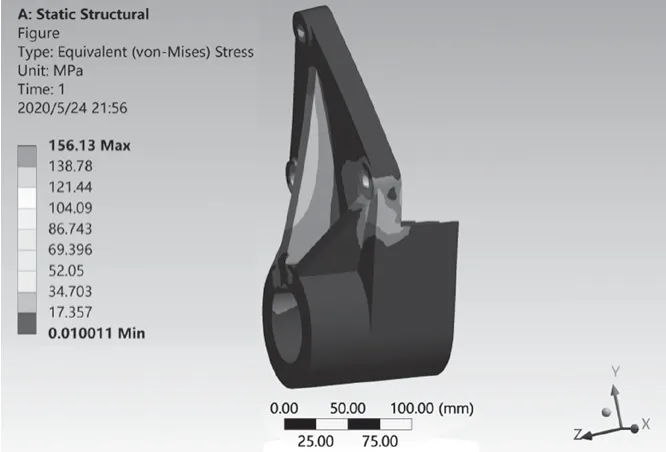
图6 尺寸优化后等效应力云图Fig.6 Equivalent stress cloud after size optimization

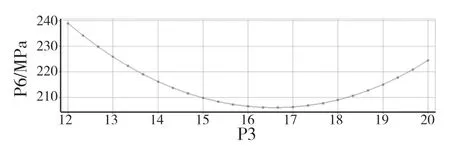
图7 大筋板厚度P3-T2-最大等效应力Fig.7 Large rib thickness P3-T2-Maximum equivalent stress

图8 小筋板厚度P2-T3-最大等效应力Fig.8 Small rib thickness P2-T3-Maximum equivalent stress

为更加全面地了解设计变量安装板厚度、大筋板厚度以及小筋板厚度对目标函数质量、总变形量以及等效应力的影响程度，找到影响目标函数的关键因素[5]，各设计变量对目标函数的灵敏度分析结果如图9 所示。

图9 全局灵敏度分析结果Fig.9 Global sensitivity analysis results

由图9 可知，设计变量安装板厚度对质量、总变形量以及等效应力的影响最为显著；其次是设计变量小筋板厚度对最大等效应力影响较为显著，对其余目标函数没有太大影响；设计变量大筋板的厚度对3 个目标函数几乎没有影响。

3 拓扑优化

在对板簧支架安装板厚度、大筋板厚度以及小筋板厚度尺寸优化后最优解模型的基础上进行拓扑优化，去除对最大总变形量以及最大等效应力影响较小的材料。

利用Workbench 中Topology optimization 模块进行拓扑优化，优化区域及非优化区域的选择[1]如图10 所示，拓扑优化后的结果如图11 所示。

图10 优化区域及非优化区域Fig.10 Optimized area and non-optimized area

图11 拓扑优化结果Fig.11 Topology optimization results

4 基于拓扑优化的多目标结构优化

4.1 设计变量的选择

以拓扑优化后的模型为参考，分别板簧支架底部挖去与红色区域相似形状的材料，板簧支架安装板上挖去近似于一个三角行的材料，以三角形的边长L 和底部去除材料的深度H 作为设计变量进行结构优化，对设计变量进行参数化。

DS_L:三角形的边长；DS_H:去除材料的深度。

设计变量的变化范围如表2 所示。

表2 设计变量的变化范围Tab.2 Design variable range

4.2 目标函数的设置

目标输出函数为最大等效应力、最大总变形及质量[2,4]，进行参数化设置，并为其设置约束条件。

P4-质量（Geometry Mass）=最小值（Minimize）；P5-总 应 变（Deformation Maximum）≤1mm；P6-最大等效应力（Eqivalent stress Maximum）≤190 MPa。

4.3 优化结果分析

系统根据优化目标及其约束条件将设计变量组合为9 个设计点，并在其中找出最优设计点5，如图12 所示。切除深度P2-H 及边长P1-L 对最大等效应力的影响如图13、图14 所示。

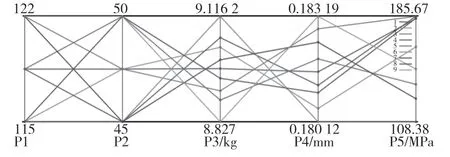
图12 设计点分布Fig.12 Design points distribution

图13 切除深度P2-H-最大等效应力Fig.13 Resection depth P2-H-Maximum equivalent stress

图14 边长P1-L-最大等效应力Fig.14 Side length P1-L-Maximum equivalent stress

优化后取值：P1-L=118.5 mm，P2-H=50 mm。将参数带回原模型，得模型质量为8.8 kg，最大总变形为0.18 mm，最大应力为174.56 MPa，总变形云图和等效应力云图如图15、图16 所示。

为全面了解设计变量三角形边长和去除材料深度对目标函数质量、总变形量及等效应力的影响程度，找到影响目标函数的关键因素[5]，设计变量对目标函数灵敏度分析结果如图17 所示。

由图17 可知，设计变量三角形的边长L 对总变形量的影响最为显著；设计变量去除材料的深度H 对质量和等效应力的影响最为显著。

图15 结构优化总变形云图Fig.15 Overall deformation cloud diagram of structural optimization

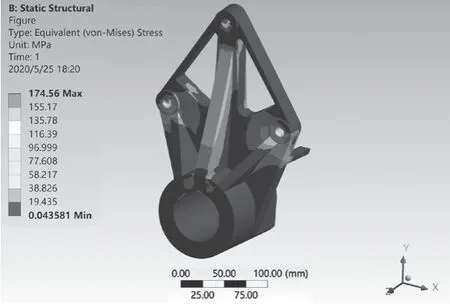
图16 结构优化等效应力云图Fig.16 Structural optimization equivalent stress cloud diagram

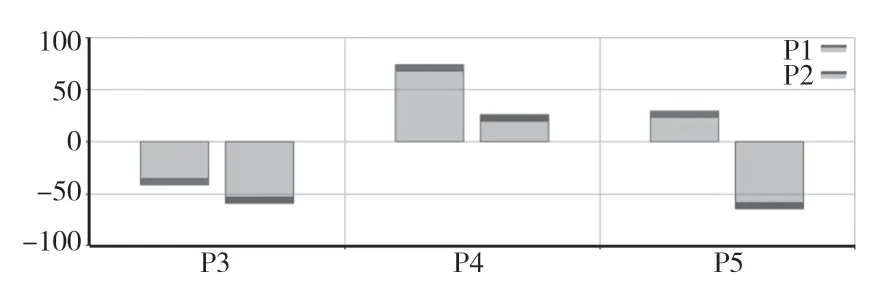
图17 全局灵敏度分析结果Fig.17 Global sensitivity analysis results

5 结论

在对板簧支架的分析过程中，虽然选用了不同的设计变量，但最终的目标是质量最轻，各个优化过程的质量、最大形变量和最大等效应力分析结果比较如表3 所示。

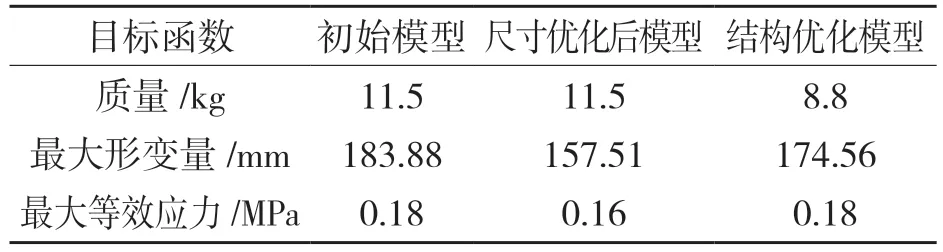
表3 分析结果比较Tab.3 Comparison of analysis results

由表3 可知，在对板簧支架进行多目标尺寸优化、拓扑优化及多目标结构优化后，相比初始模型质量减少了2.7 kg，减少了23.4%。最大等效应力减少了9.32 MPa，板簧支架强度提高了5%。