SOFC电堆降阶建模研究及其仿真测试

张 琳，刘润华，周伟彬，杜鹏飞，王晋晶

(1.空军预警学院，湖北武汉 430019；2.武汉科技大学冶金自动化与检测技术教育部工程研究中心，湖北武汉 430081)

固体氧化物燃料电池(SOFC)在众多新能源燃料电池中具有转换效率高、燃料来源广泛以及热电联供等优点[1]，其成功应用对于缓解能源危机、满足电力需求以及保障国家安全具有重大意义。目前燃料电池带外围辅助子系统BOP 集成建模及优化研究的相关报道有很多[2-7]。但是SOFC 系统具有高阶复杂非线性的特性，在建模及分析研究工作中，对SOFC 模型的温度分层以及模型降阶进行分析，设计面向控制的SOFC 系统级降阶模型，是SOFC 控制器设计的前提条件。基于以上分析，本文根据SOFC 系统结构搭建其模型并分析其状态变量，设计了SOFC 系统降阶模型，对SOFC 系统降阶模型进行了仿真测试。

1 SOFC 系统结构

本文所研究的纯氢SOFC 独立发电系统主要由五个子系统构成：燃料供应子系统，空气供应子系统，电控子系统，电堆以及尾气回收子系统，尾气回收子系统又包括燃烧室与热交换器。其基本结构如图1 所示，氢气与空气换热器利用从燃烧室出来的高温尾气进行换热，形成尾气回收子系统，电堆在内部产生电化学反应，产生电能。此外，在空气主干道上增设了一条冷空气旁路，通过对其开度的调节，可以有效控制电堆工作温度及其温度梯度。

图1 SOFC独立发电系统示意图

2 SOFC 系统建模与状态变量研究

基于SOFC 系统工艺结构，需要在Matlab/Simulink 进行仿真建模分析。主要模型部件为：SOFC 电堆、热交换器(两级)、燃烧室。主要建模思想为电堆一般假设由连接层、燃料管道、空气管道、PEN(positive-electrolyte-negative)这四个温度层组成[8-9]，如图2 所示。由于电堆内温度梯度需要重点观测，热交换器中管道太长，温度变化过大[10]，SOFC 电堆和热交换器的模型搭建采用1D 模型，基于节点思想进行建模[11]，其他部件模型均采用0D 模型。很多学者基于实际应用搭建了SOFC 系统模型[12-14]。本文主要搭建5 kW SOFC 系统模型，组成电堆的单电池片以及热交换器可分为5 个节点，电堆由130 个单电池片组成，单电池片面积为11 cm×11 cm。高阶非线性SOFC 动态模型搭建及模型验证过程在前期工作中已有相关基础[15-18]。

图2 SOFC独立发电系统模型搭建示意图

从控制角度出发，需要分析SOFC 独立发电系统动态模型的系统输入输出参数以及状态参数。SOFC 系统内的状态向量主要包括两个方面：一是系统流体以及部件的温度，二是系统内流体的摩尔分数，温度(T)和摩尔分数(X)。热交换器(两级)每个节点温度参数主要由固体控制单元温度(空气管道，燃料管道以及尾气管道)以及气体控制单元温度(空气端，燃料端以及尾气端)两部分组成，共有6 个温度状态，则两个换热器共有60 个状态变量；电堆内温度特性包括四个温度层(空气、燃料、连接层、PEN)温度，流体特性包含空气、燃料、水蒸气的摩尔分数特性，则SOFC 单电池片内部包含4 个温度状态与3 个物质状态，共35 个状态变量；本文所搭建的燃烧室主要包括燃烧室温度以及燃烧尾气温度2 个状态变量。则SOFC 系统一共包含97 个状态变量，具有复杂的高阶非线性、多状态变量以及时变特性。因此，需对系统级SOFC 进行降阶。

3 基于SOFC 系统降阶模型设计

由于系统的建模复杂度主要集中在1D 的换热器及电堆，因此，模型降阶的主要工作就是对换热器和SOFC 电堆进行化简。蒋[2]已经做了相关工作，通过对换热器模型的简化，减少了48 个温度状态变量；电堆模型中根据准静态假设，得到质量守恒方程，极大地降低了系统的复杂度。SOFC 电堆具有四个温度层，将电堆的温度层分情况进行组合，分别简化至1～3 层。为此，本文同时搭建了4 温度层模型，分析它们的输出特性，并与原模型进行比较。具体层数及其假设如表1 所示。

表1 温度层假设

4T模型4 个温度层(PEN 层、连接层、空气层、燃料层)计算公式如式(1)～(4)所示。

式中：vPEN、ρPEN和Cp，PEN分别代表PEN 单元的体积、密度和比热容；qcond,PEN代表热传导量；τPEN代表PEN 厚度；kf,PEN和ka,PEN分别代表燃料及空气端与其PEN 侧的热传递系数；i代表电流密度；F为法拉第常数；hH2(Tf)、hO2(Ta)和hH2O(TPEN)分别代表H2在Tf温度，O2在Ta温度和H2O 在TPEN温度时的比焓；Ucell代表单电池片的电压；σ 为斯蒂芬波尔兹曼常数；εI与εPEN分别代表连接端与PEN 端的放射率。

式中：Sf代表燃料端气体，Sf∈{H2,H2O}；Cp,Sf代表燃料端气体的定压比热容；R为通用气体常数；NSf为燃料端气体的摩尔数；qin,f和qout,f分别表示燃料进口和出口的焓通量；kf,PEN和kf,I分别表示电堆燃料及其连接端的热传递系数；Ac,f，Ac,n分别表示燃料管道和反应气体的横截面面积；hSf表示燃料端气体比焓。

式中：Sa代表空气端气体，Sa∈{O2,N2}；Cp,Sa代表空气端气体的定压比热容；NSa为空气端气体的摩尔数；qin,a和qout,a分别表示空气进口和出口的焓通量；ka,PEN和ka,I分别表示电堆空气及其连接端的热传递系数；Ac,a表示空气管道的横截面面积；hSa表示空气端气体比焓。

式中：ρI和Cp，I分别代表连接体层单元的密度和比热容；qcond,I代表热传导量；τI代表连接体层厚度；kf,I和ka,I分别代表燃料及空气端与其连接体层侧的热传递系数。

3T模型3 个温度层(固体层、空气层、燃料层)计算公式如式(5)～(7)所示。

4 简化后的系统仿真测试

通过对电堆和换热器模型的简化，以2T模型为例，SOFC电堆模型的每一个节点就只有2 个温度状态变量，SOFC 电堆模型的总状态数为10 个。但是简化后性能是否可靠，能否保持原系统模型的特性是简化过程中必须考虑问题之一。为了验证模型的可靠性，从动静态性能两个方面，比较简化模型与原模型在不同功率输出情况下的差异。表2 为系统静态性能输入参数。

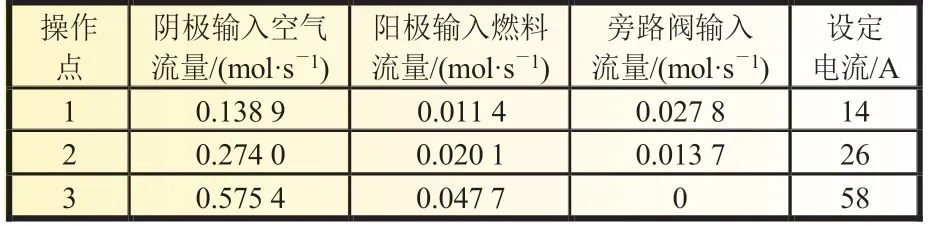
表2 系统静态性能输入参数

为了分析SOFC 系统的静态特性，需要从热电特性与流体特性方面进行分析。电特性参数重点分析V-P特性以及简化模型电堆不同温度层的电流密度分布，如图3 所示。不同模型(2T、3T、4T)在不同操作点(1、2、3)的单电池片输出电压、系统输出功率数值基本相同，其简化模型与复杂的4T模型V-P特性曲线基本相似；稳态条件下不同操作点下的电堆模型电流密度分布基本相同。简化模型中2T模型与4T模型的电特性输出参数更为接近。

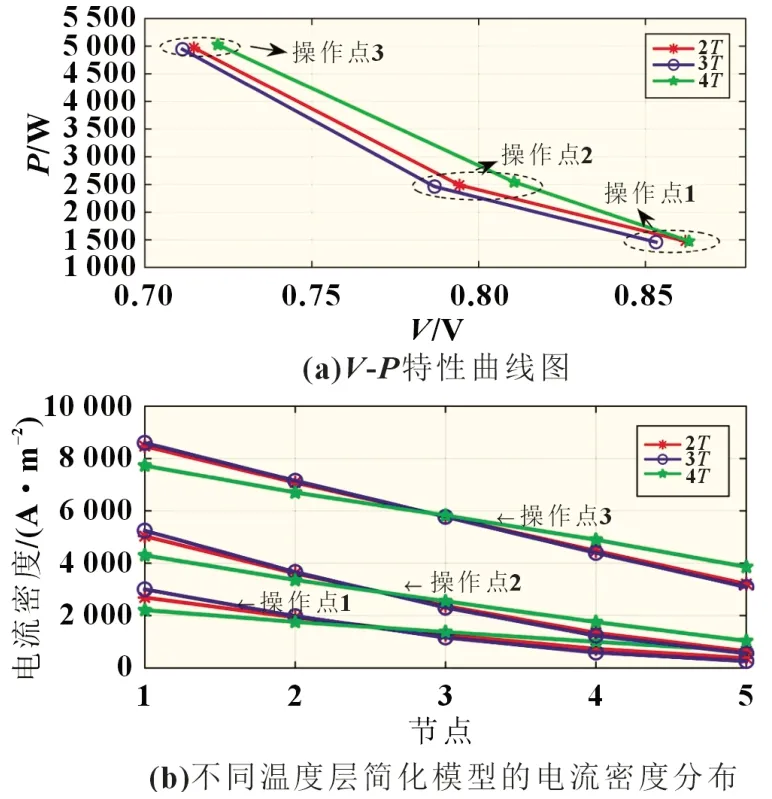
图3 SOFC 系统的电静态输出特性

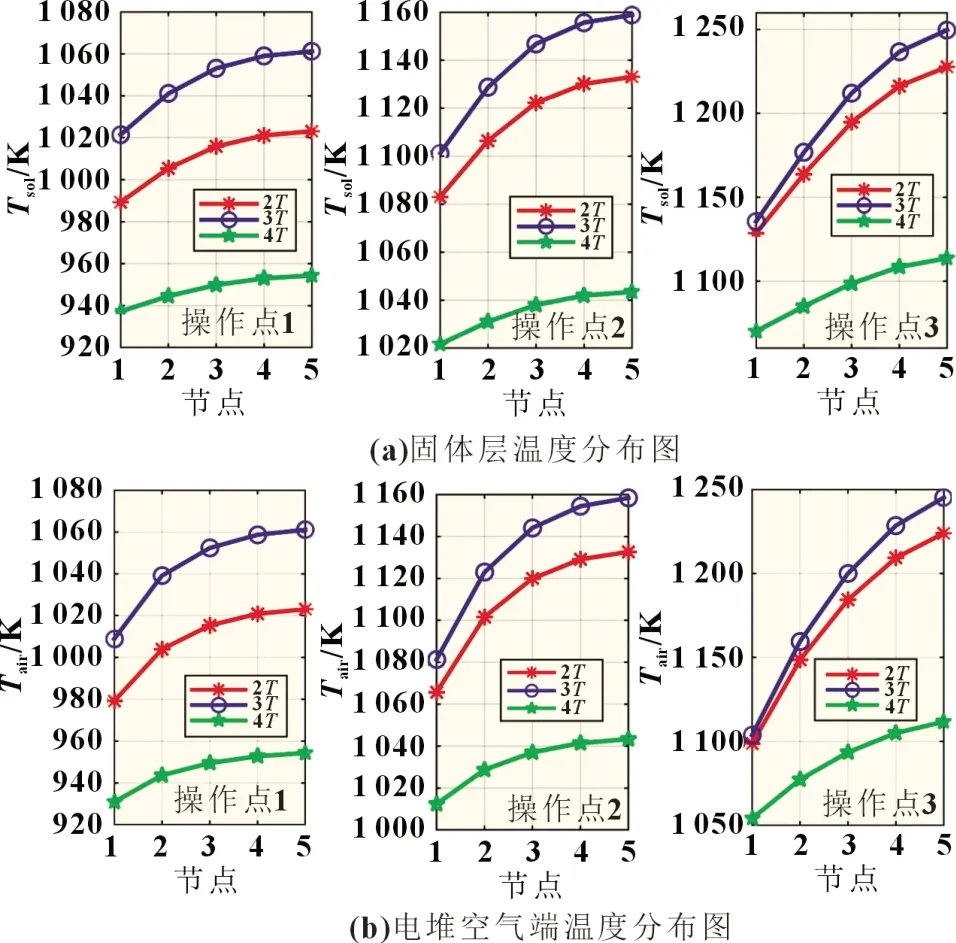
图4 SOFC系统的热静态输出特性

静态热特性参数输出特性如图4 所示，分析了固体层温度分布与电堆空气端温度分布。各个电堆节点温度存在差异，其温度差异是由于单电池片模型搭建过程中降阶温度层所致，其误差范围控制在150 K 之内。温度静态输出分布趋势基本相似。

静态流体特性参数的输出特性如图5 所示，分析了电堆内H2O、H2、O2在各个节点的稳态输出，不同操作点下2T、3T、4T模型电堆内H2O、H2、O2在各个节点的稳态输出数值与分布变化趋势基本相近。同样，2T模型与复杂4T模型的流体特性参数静态输出特性最为相近。以上分析说明本文所搭建的简化模型在SOFC 静态特性方面是有效的。

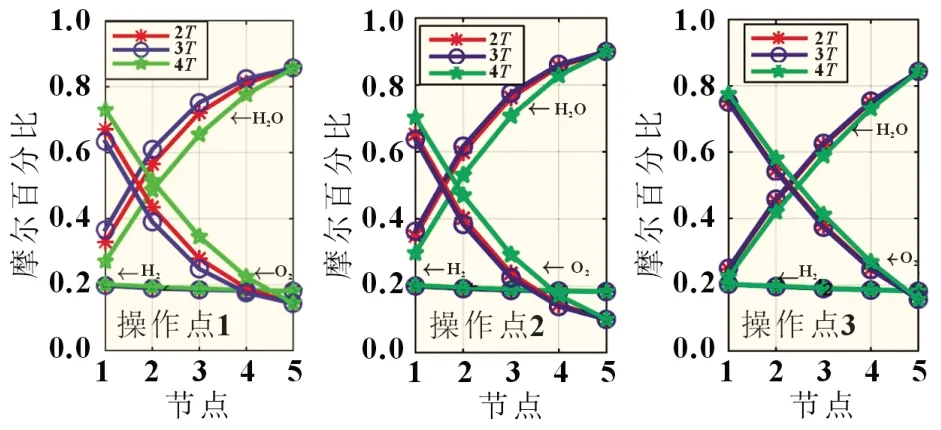
图5 SOFC 系统的流体静态输出特性

由于后期控制器设计重点考虑系统的热电动态响应，分析了热电静态输出特性，其误差值可表示为：

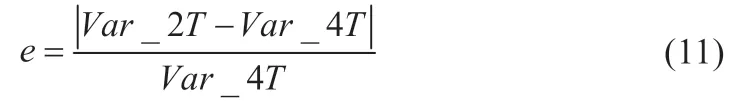
式中：e代表误差；Var_2T代表2T模型的变量；Var_4T代表4T模型的变量。误差值如表3 所示。

由表3 可知，系统静态输出功率误差最大值为2.2%，静态输出电压误差最大值为2%，均在可接受范围以内；其热静态特性输出值误差相对较大，随着电堆节点增大，误差变大，固体层温度最大误差值为10.3%，空气层温度最大误差值为10%。为了提高控制精确性，后期控制器设计中可根据仿真结果进行温度补偿。

为了从动态响应上分析简化模型的准确性，在5 000 s时，系统从表3 中的操作点2 稳态工作阶跃到操作点3 输出特性，对系统电输出特性进行分析，如图6 所示。各温度层模型节点1 和5 的电流密度阶跃响应过程中，各模型的变化趋势基本一致，响应时间尺度相同；各模型单电池片的输出电压与系统输出功率基本相似，其误差在可接受范围之内。

表3 系统静态性能输出误差值

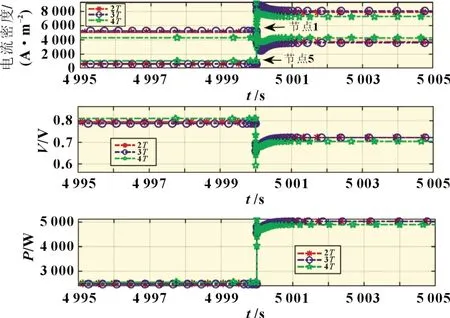
图6 SOFC系统的电动态输出特性

5 结论

总的来说，SOFC 不同温度层模型的电静态输出特性(V-P特性曲线、电流密度分布)、流体静态输出特性(H2O、H2、O2)在不同操作点的稳态输出数值与分布变化趋势基本相近，热静态特性输出(固体层、电堆空气端温度分布)由于温度层降阶，误差较大，后期控制器设计时需进行温度补偿；静态输出特性均能够非常准确地反映原物理模型的稳态输出性能，可以作为控制器设计的依据；动态输出特性(电流密度、输出电压、输出功率)的响应趋势基本一致，响应时间尺度相同，所以可以认为简化温度层模型有效地保留了原模型的特性。此外，对比动静态特性可知，2T模型不仅大幅度地减少了模型的复杂度，而且还很好地保持了原模型的动静态特性，在模型精度与复杂度上做了更好的折中，应优先在控制器中采用。此研究结果对SOFC 燃料电池独立发电系统的建模和控制具有一定的实用价值。