基于逐步回归的PVT-M建筑不舒适度小时数预测模型分析
钟胜利,林尧林,黄兴华
(1上海工程技术大学 机械与汽车工程学院,上海 201620;2上海理工大学 环境与建筑学院,上海 200093)
0 引 言
随着经济的快速发展和人们生活水平的提高,人们对改善居住环境条件的需求不断增加。然而,在建筑能耗日益增长的趋势下,大多数建筑设计者及研究人员往往关注的是如何降低建筑能耗,却忽略了室内的环境质量,这一现象容易产生病态建筑综合征(SBS)[1]。不舒适小时数作为衡量建筑性能的重要指标之一,受建筑围护结构传热系数、窗墙比、建筑表面太阳热吸收率等诸多建筑热物理参数的影响[2]。
目前,通过数据挖掘软件与模型预测技术,可以获取影响不舒适小时数参数的基础数据,并建立相关预测模型,使设计者在建筑设计早期快速准确的获得室内热舒适情况,从而为居住者提供一个健康舒适的室内环境。
关于利用逐步线性回归方法建模和预测方面,蒲清平等[3]通过SPSS软件建立了居住建筑能耗预测的逐步线性回归模型,并对模型的拟合效果进行了检验。结果表明,模型预测年能耗与实际统计年能耗符合度达95%左右,说明模型具有较高的预测精度和较好的拟合效果;Amiri等[4]采用逐步线性回归方法,建立了建筑能耗预测模型,并将预测与模拟结果进行对比分析。结果表明,二者之间的误差是可以接受的,同时指出该方法简单,能够准确快速地对建筑能耗进行预测;Braun等[5]利用逐步回归方法,分别建立了燃气消耗和电力消耗预测模型,并将预测值与实际值进行了比较。结果表明,两个模型的预测值都是令人满意的;Hygh等[6]采用逐步线性回归的方法,建立了4个城市不同气候区供热、制冷以及总能耗的预测模型,并与EnergyPlus模拟结果比较。结果显示,预测数据与模拟结果吻合较好,同时也表明在设计初期,线性回归可以作为一种有效的简化模型来代替能耗模拟模型。
在热舒适性建模与预测方面,孙斌等[7]利用BP网络、GA-BP网络、RBF网络及Elman网络,分别建立了热舒适性指标预测模型。结果表明,GA-BP神经网络的预测性能最佳,并指出其对权值和阈值的优化是以训练时间为代价的;喻伟等[2]考虑到14个变量对建筑能耗和室内热舒适状况的影响,并建立了GA-BP网络模型。通过对样本数据进行训练和测试,验证了该模型具有较高的预测精度,同时表明人工神经网络预测精度受样本数据的影响;陆烨等[8]采用PSO-RBF的方法,建立了PMV指标预测模型,实现了对PMV指标的智能预测,并通过仿真计算表明,PSO-RBF网络的预测误差精度提高了79.5%,小于RBF网络;朱婵等[9]提出了一种基于改进的禁忌遗传算法神经网络的热舒适度预测模型(TGA-BPNN),通过仿真实验并与BP神经网络及遗传神经网络相比,TGA-BPNN可以进一步提升模型预测的准确性,同时表明采用此方法存在算法运行时间长、空间复杂度大以及效率低等不足。
综上所述可以发现,利用逐步回归方法进行预测主要是针对建筑能耗,而对热舒适性等建筑环境领域的研究很少。回归模型不仅结构简单,而且可以达到准确可靠的预测效果。而对于热舒适性的预测普遍采用神经网络。然而,利用传统的神经网络进行预测时,其预测结果误差往往取决于样本数据。大部分文献都采用算法与神经网络结合的方式,来提高预测精度。但其结构复杂程度会随之增加,算法运行效率也会有所下降,即耗时又耗力。因此,本文采用逐步回归方法,建立了集成PVT-M建筑的不舒适度小时数预测模型,并对模型的准确度以及预测变量的重要性进行了分析。
1 建筑模型及参数变量
1.1 居住建筑模型
本文选取的居住建筑位于上海市,典型气候特征为夏季闷热,冬季湿冷。该气候区的建筑物必须满足夏季防热、通风降温要求,冬季应兼顾防寒取暖需求。
利用DesignBuilder建立了建筑模型,如图1所示。建筑面积100 m2,高度4m,为了建筑在冬季能获得更多的太阳辐射获得热量,建筑朝向采用了该地区最佳的南偏东15°方位。建筑采用光伏板、相变材料和特朗伯集热墙(Trombe wall)结构。光伏板布置在屋顶,主要提供室内用电设备的能源消耗;建筑南向为带有相变材料的特朗伯集热墙,分为内层、中间层和外层3层。内层墙体结构为面砖层、XPS保温层、混凝土层、相变材料层、石膏抹灰层,墙体上开了两个通风孔,其主要作用是结合中间层的空气腔来实现建筑的自然通风,从而降低室内的冷热负荷,外层为玻璃幕墙。其它3面墙体都设置了外窗,且采取了遮阳措施。

图1 建筑模型图Fig.1 Building model diagram
1.2 参数变量
1.2.1 自变量
本文选取的34个参数变量都是查阅相关文献以及规范标准获取的,参数涉及窗墙比、保温层厚度、混凝土厚度、太阳热吸收率、外窗类型、遮阳类型、夏季室内空调和冬季室内采暖温度设定值、相变材料的类型、厚度以及相变温度、光伏板的倾角和面积、Trombe墙的空腔厚度、幕墙厚度和通风口面积等。具体变量类型及取值范围见表1。
表1中:G1-G16表示16种不同的外窗类型;L1-L9表示9种不同长度厚10 cm的悬挑混凝土板;P1-P5表示5种不同的相变材料;W6-W10表示5种不同厚度的玻璃幕墙,这些变量均属于离散型变量。
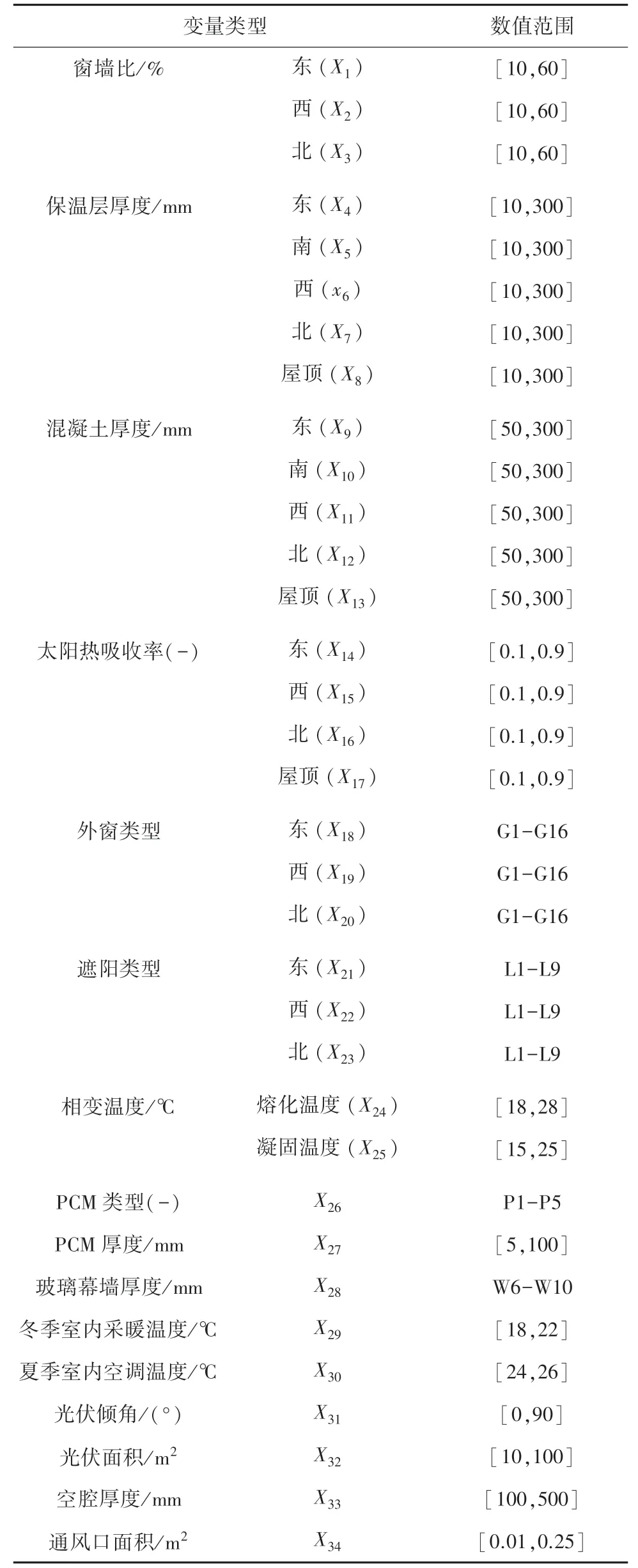
表1 变量类型及数值范围Tab.1 Variable type and numeric range
1.2.2 因变量
本文选取的目标函数为不舒适度小时数,可分为夏季不舒适度小时数和冬季不舒适度小时数,其数学表达式为[10]:

式中,T1为全年高于26℃的室内空气温度,T2为全年低于18℃的室内空气温度。
2 建立预测模型
2.1 数据采集
充足的样本量是保证预测模型稳定性和准确性的关键。为了建立不舒适度小时数预测模型,需要建立一个以建筑设计参数为输入,以不舒适度小时数为输出的数据库。本文采用了20世纪40年代由S.Ulam提出的蒙特卡洛抽样方法(MCM)[11],MCM是一种随机模拟抽样方法,其工作原理如下:
(1)构造或描述概率过程;
(2)实现从已知概率分布抽样;
(3)建立各种估计量。
利用该方法对选取的34个变量进行抽样,最终确定了1 000个样本。通过仿真软件DesignBuilder对样本进行模拟,来获取不舒适度小时数。
2.2 逐步线性回归模型(SLR)
线性回归分析方法已被普遍应用于不同建筑的性能预测。S.Asadi等[12]发现多元线性回归模型在建筑设计阶段的早期应用,可以提高能源效率和减少排放。逐步线性回归模型(SLR)属于线性回归的一种,由于变量个数和回归模型的复杂性会对模型拟合优度产生显著影响,逐步线性回归可以采用正向选择和逆向淘汰相结合的方法实现自动选择自变量,从而确定自变量对因变量的影响程度大小。其模型描述如下:
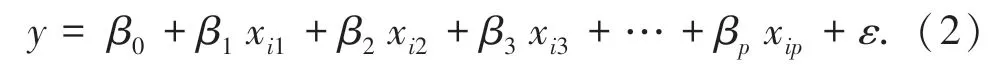
式中,β0为回归常数,β1,β2,β3,…,βp为回归系数,通过最小二乘法确定回归系数,使平方和误差最小。
3 逐步线性回归结果分析
3.1 逐步线性回归方程
利用IBM SPSS Modeler数据挖掘软件建立了不舒适度小时数逐步回归模型,模型结构如图2所示。采用步进(条件:当候选变量中最大F值的概率≤0.05时,引入相应变量;在引入方程的变量中,最小F值的概率≥0.1时,则剔除该变量)的方法,选择进入或除去的自变量。在34个建筑设计参数中,逐步回归方法建立的不舒适度小时数回归模型保留了22个参数。

图2 逐步回归模型结构图Fig.2 Stepwise regression model structure diagram
在回归模型中,一般P≤0.05则认为具有显著性,根据未标准化系数B值可以得到式(3)所示的不舒适度小时数回归方程。不舒适度小时数回归模型变量的回归系数以及显著性P值见表2。从表中可以看出,不舒适度小时数回归模型的变量回归系数所对应的P<0.05,说明模型的自变量和因变量之间有明显的线性关系,建立的回归方程是有效的。
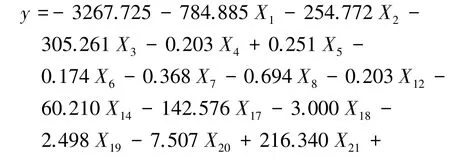

在进行线性回归分析时,共线性会使参数估计不稳定。方差膨胀因子(VIF)可以检测多重共线性,它和容差(Tolerance)互为倒数关系,当VIF≥10时,说明变量之间有严重的多重共线性,其值越接近1,变量之间多重共线性越弱。从表2统计的数值来看,不舒适度小时数回归模型相关变量的VIF均在1附近,说明这些变量之间共线性较弱。
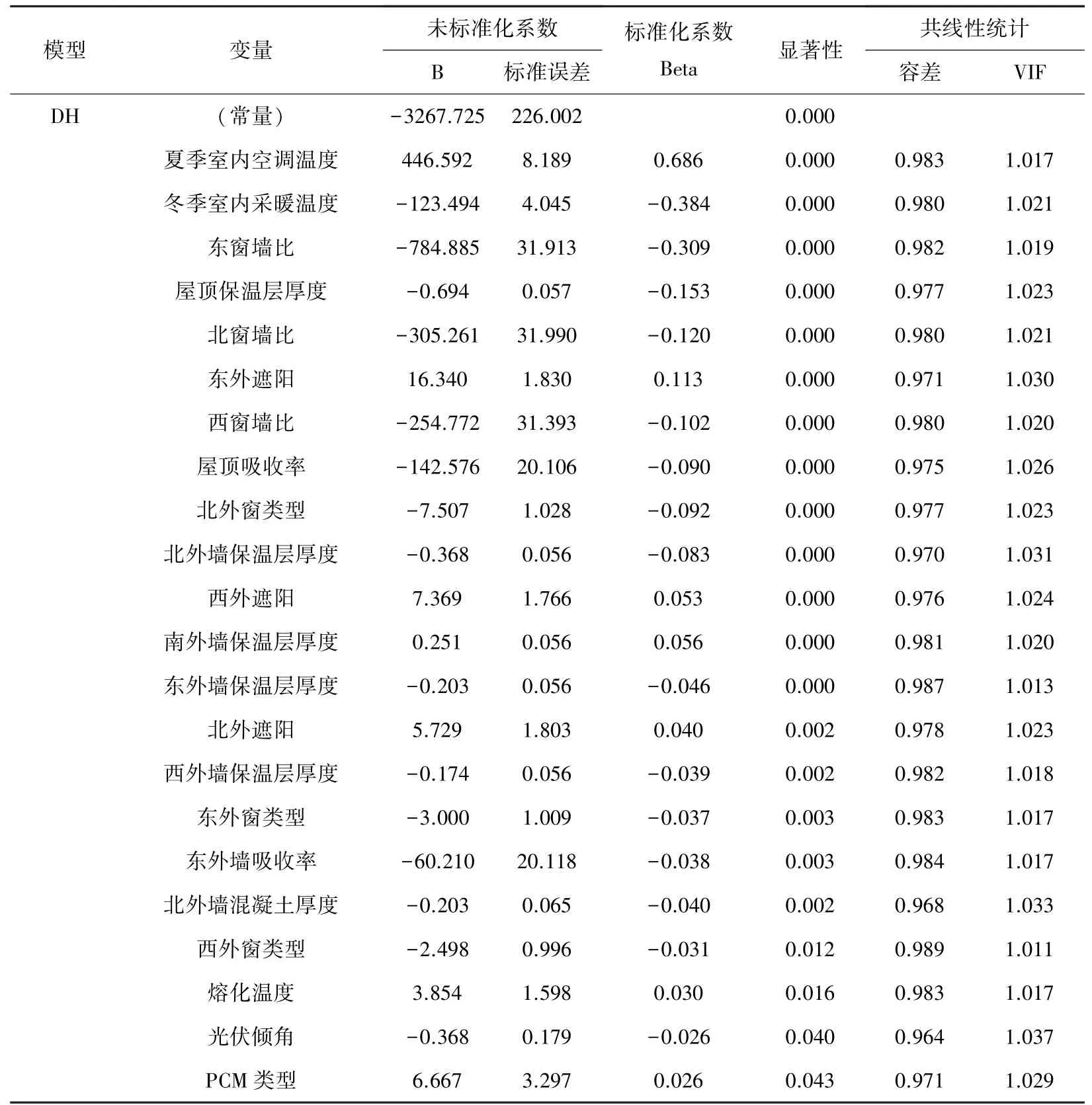
表2 逐步回归系数Tab.2 Stepwise regression coefficient
3.2 回归模型拟合优度检验
回归方程的拟合优度检验,是检验样本数据聚集在样本回归直线周围的密集程度,从而判断回归方程对样本数据的代表程度。拟合优度检验一般采用调整决定系数R2实现,该统计量的值越接近于1,拟合优度越好,R2可由式(4)-式(8)计算得到。
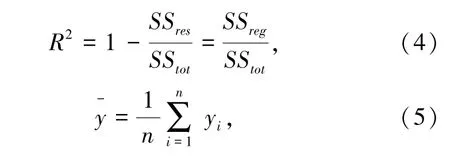
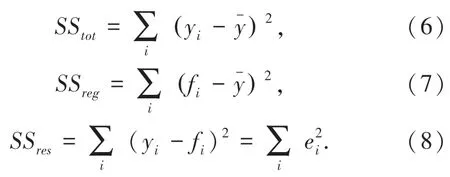
式中,S Sreg为回归平方和;S Sres为残差平方和;S Stot为总平方和;yi为真实值;fi为预测值;y-为平均值。
不舒适度小时数模拟值与SLR预测值的回归如图3所示。可以看出,模拟和预测的数据结果有很好的一致性,不舒适度小时数回归模型的R2为0.845,显示出较好的拟合效果。
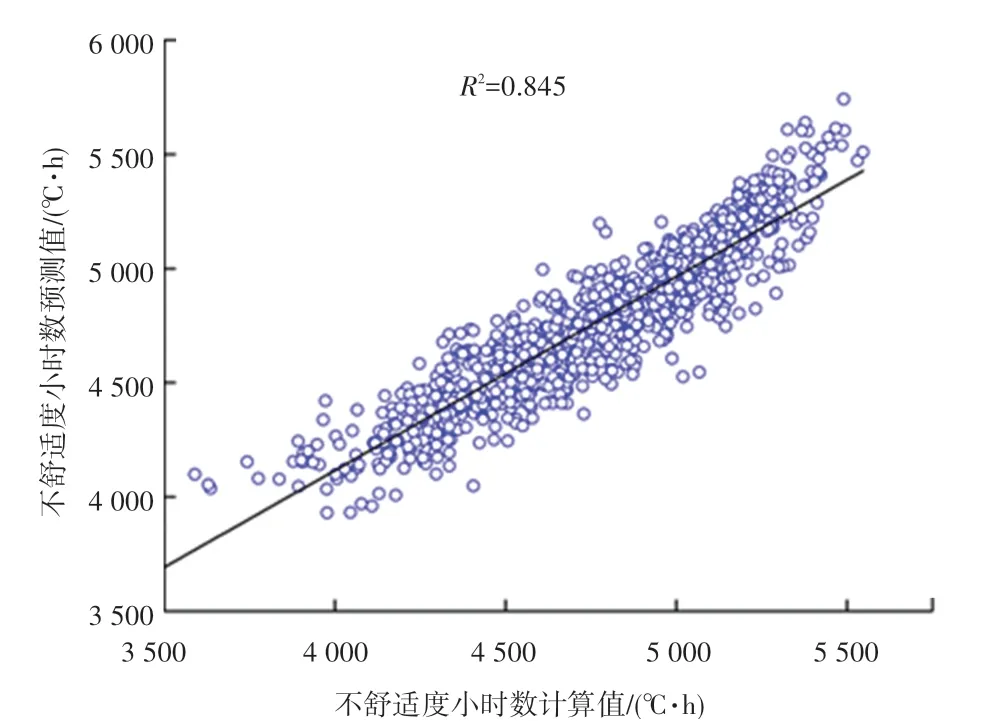
图3 不舒适度小时数模拟值与SLR预测值回归图Fig.3 Regression diagram of simulated value of discomfort degree hour and SLR predicted value
一个好的线性回归模型必须满足相关的所有假设,其中包括线性、独立性、正态性、方差齐性等。图4给出了不舒适度小时数回归模型的标准化残差正态概率P-P图。由图可见,所有的点都比较靠近对角线,且结合残差统计表3得到的不舒适度小时数回归的标准偏差为0.989(<2),说明回归模型的残差是呈正态分布的。

图4 不舒适度小时数标准化残差正态概率P-P图Fig.4 P-P graph of standardized residual normal probability of discomfort degree hour

表3 不舒适度小时数残差统计表Tab.3 Residual statistical table of discomfort degree hour
3.3 回归模型误差分析
为了评价不舒适度小时数逐步回归模型的准确度,采用相对误差(RE)这一指标来进行衡量,其数学表达式如下:

式中,RP为利用SPSS软件线性回归的预测值,RS是利用DesignBuilder仿真软件的计算值。
表4给出了1 000组预测样本数据的相对误差范围。由此可见,利用SLR方法预测的不舒适度小时数最大值和最小值分别为5741.61和3791.59,相对误差的最大值和最小值分别为16.03和-10.32,再结合图5统计的不舒适度小时数相对误差分层梯度范围可以得出:相对误差范围在10%-20%的样本只有8组,占样本总数的0.8%,绝大多数样本相对误差范围小于10%,其中相对误差小于2.5%更是达到了一半以上,说明利用SLR能达到对不舒适度小时数较好的预测效果。
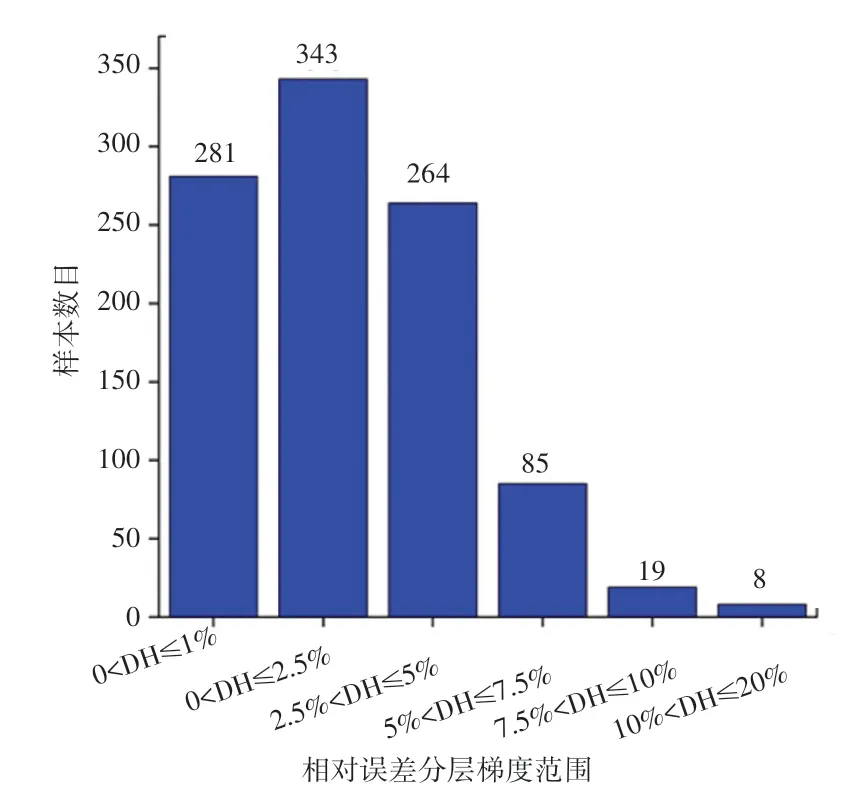
图5 不舒适度小时数相对误差分层梯度范围Fig.5 Relative error stratified gradient range of discomfort degree hour

表4 不舒适度小时数相对误差范围Tab.4 Relative error range of discomfort degree hour
3.4 预测变量重要性分析
依据表2中列出的22个参数变量,为了分析每个自变量对不舒适度小时数的影响程度大小,采用单个自变量标准化系数值的绝对值与方程相关的所有自变量的绝对值和的比值作为评价标准。
通过表2的标准化系数,可以计算得到每个自变量所占比例大小,其统计结果如图6所示。从图中可以看出,夏季室内空调温度对不舒适度小时数的影响程度最大,其次为冬季室内采暖温度和东向窗墙比。前三者标准回归系数所占比值分别为26.4%、14.8%和11.9%,PCM类型和光伏倾角对不舒适度小时数的影响程度最小,所占比例只有1%。

图6 预测变量影响程度大小Fig.6 The degree of influence of predictive variables
4 结束语
本文利用逐步回归方法,建立了集成PVT-M建筑不舒适度小时数模型。通过对模型分析,可以得到以下结论:
(1)在选取的34个设计变量中,利用逐步回归方法建立的不舒适度小时数回归方程中保留了22个参数,同时通过显著性P值验证了方程的有效性。
(2)在模型拟合优度方面,不舒适度小时数SLR模型的回归系数为0.845,说明计算数据与预测数据之间具有较高的线性拟合度。
(3)在回归模型误差方面,相对误差范围小于2.5%的样本数占半数以上,只有极少一部分样本相对误差范围较大,说明SLR是一种可行的模型预测方法,能实现对不舒适度小时数的准确预测。
(4)在预测变量重要性方面,对不舒适度小时数影响程度最大的为夏季室内空调温度,影响程度最小的为PCM类型和光伏倾角。

