基于感应学习网络的科技成果转移预测模型与仿真

汪杰

（北京化工大学，北京 100089）

社会的发展离不开科技的进步，科学技术是第一生产力，我国每年均在鼓励社会各界进行科技创新，社会每年都在产生着大量科技成果。科技成果的转化是科技成果变为社会生产力、创造价值的重要一步，科技成果的转化过程主要包含3 个步骤，分别是基础研究、技术研究与产品研究。首先在基础研究上，科研院所通过相关基础理论的研究在某一领域形成知识形态；接着研发部门根据市场信息进行技术研发，将理论转化为技术，形成准商品；最终在产品研发阶段，技术产品转移至生产企业，企业经产品孵化，借助规模化的成品产生社会价值[1-6]。

科技成果的转移是一项涉及面广、流程复杂的系统工程，在这一过程中，会花费大量的人力、财力资源。若能够在科技成果孵化为产品之前即可通过智能化的算法预测其社会收益，则对于科学合理地进行科技项目立项、规划科技投资具有重要的指导意义[7-16]。基于以上目的，该文对科技成果的转移预测进行了相关研究，并对科技成果的转移流程进行数学建模，同时介绍该文使用的感应学习网络理论，使用生产中的实际数据进行仿真，从而验证该文模型与算法的有效性。

1 理论基础

1.1 系统建模

在该文的引言阶段，已对科技成果转化的各个阶段内容进行了简要说明。该文的目的在于通过引入先进的计算机算法，利用科技成果转化过程中的多方面数据，预估成果转移的社会效益。因此，仍需对上述过程进行数学化的抽象。通过研究发现，从数学建模的角度出发，科技成果的转移过程可以分为成果的形成、小型试验、中期试验与产品诞生4 个阶段。为了承接这4 个阶段中的数据流，该文设计了科技成果转移过程流程图，如图1 所示。

图1 中包含4 个子系统与系统间的数据流向，这4 个子系统分别是针对科技成果进行技术研发的子系统H1；对科技成果进行技术改进的子系统H2；进行中期试验的中试转化系统H3 与进行新产品生产的系统H4。每个子系统均有其需要的初始启动费用Wi；在各个系统实验中，又会引入新的经费投入Qi；在科技成果转移过程中，每个阶段均会产生一定的成果Ri；系统中还存在表征成果转移效率的变量Ki。系统的变量说明如图2 所示。

在图2(d)中，根据其定义方法，计算方式如下：

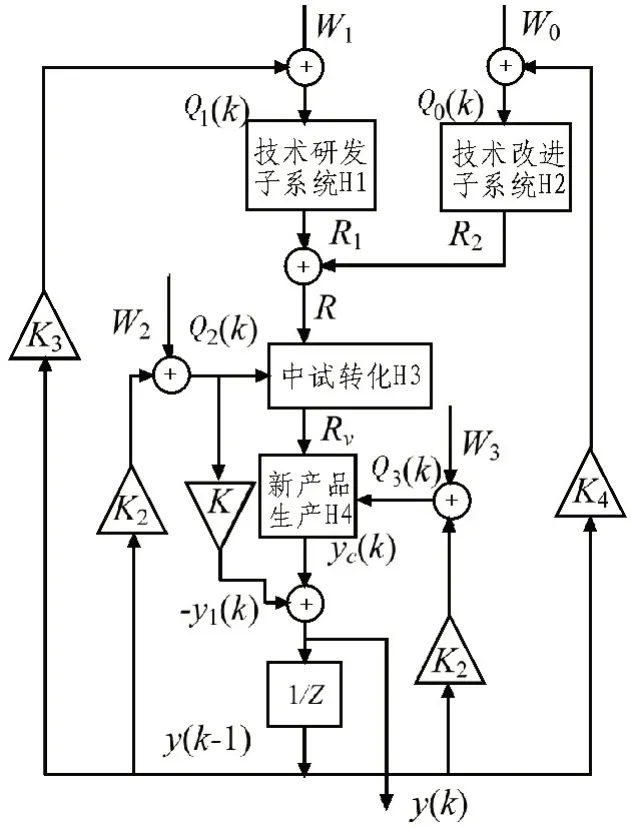
图1 科技转化流程建模

图2 系统中变量说明

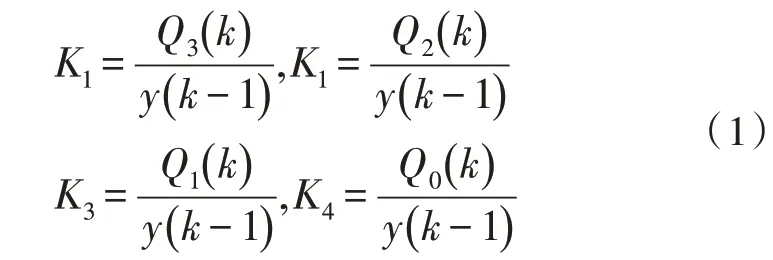
1.2 感应神经网络

1.1节中建立了科技成果转移的数学模型，该模型可以定量描述科技成果转移过程中的数据流向。为了通过这些数据流向准确地预测一项新的科技成果的社会效益，需要再引入计算机智能算法，该文使用的计算机智能算法是感应神经网络。在机器学习理论中，将无监督的神经网络称为感应神经网络，而自组织神经网络即是一个典型的感应神经网络，其基本结构如图3 所示。

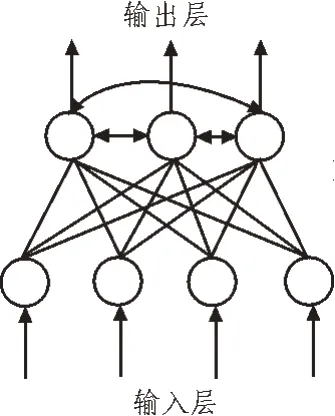
图3 自组织神经网络结构

自组织神经网络的学习过程分为3 个子过程：竞争、合作与自适应。

1）竞 争

对于一个自组织网络，其输入为x、输入层到竞争层的连接向量wj分别可以记为式（2）。

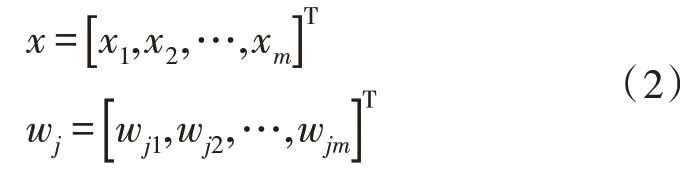
其中，网络在竞争层中有l 个单元，式（2）中的j=1，2，…，l。

竞争的依据为x与wj间的欧式距离或余弦距离。x与wj间距离最小的输入向量为竞争的胜利者，其对应的输入神经元被选择为当前网络的输入神经元。两种距离各自的计算方法，如式（3）所示。

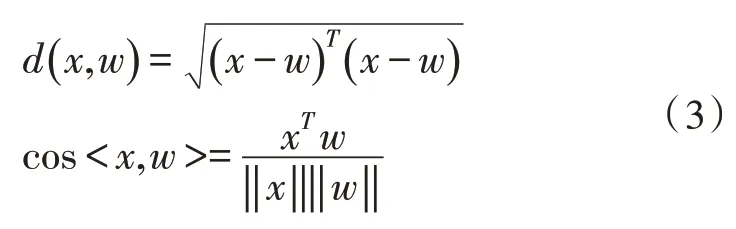
2）合 作

竞争仅是确立了最佳的输入神经元，但一个网络仅依靠一个神经元是不具备较强的分类性能。因此，自组织神经网络还会在最佳神经元的邻域内选择合作神经元。该邻域以最佳神经元为圆心，以距离hj,i为半径，该邻域的确定依托于两个条件：

1）当邻域内的神经元到最佳神经元的距离di,j＝0 时，hj,i最大；

2）hj,i是关于di,j的单调递减函数。

根据上述的两个条件，该文选择的di,j与hj,i关系函数为Guass 函数，如式（4）所示。

通过引入式（3），使得hj,i只受合作神经元与最佳神经元距离影响，剔除了最佳神经元坐标变换引起的抖动。对于二维的神经元网格，其di,j的计算方法如式（5）所示。

在自组织神经网络训练的过程中，为了保证训练的效果，可以将式（4）中ξ设置为关于训练时间的变量，如式（6）所示。

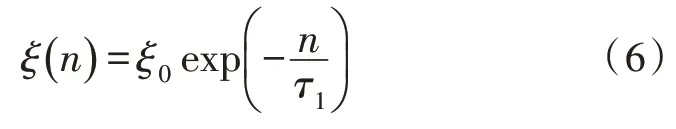
其中，n=0，1，2…。根据式（6），hj,i的最终形式可写为式（7）。

3）自适应

自适应过程是指在训练过程中，网络连接权值随误差反向传播而更新，随着网络自适应进程的推进，自组织网络逐渐达到理想的输出。在每一次迭代中，权值的变化定义如下：

其中，η是网络的学习率；g(yj)是一个线性函数，如式（9）所示。

将yi写成(yj)=hj,i(x)。此时，Δwj如式（10）所示。

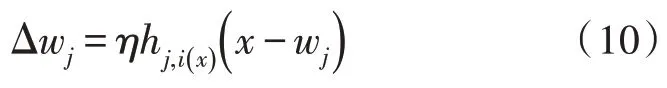
最终可以得到n到n+1 时刻权值wj(n+1)的变化公式，如式（11）所示。

2 方法实现

2.1 算法流程设计

基于以上分析，将自组织神经网络与科技成果转移预测的系统模型相结合，设计基于感应学习网络的科技成果转移预测模型的方法流程，如图4所示。

该文选取的数据是某科技集团的30 个科技项目。在数据的预处理上，按照图1 的数据模型进行整理，并将数据进行归一化。在数据集的划分上，选取其中20 组作为模型的训练数据、10 组作为测试数据。模型的参考函数选择K-G 多项式，其形式如下：

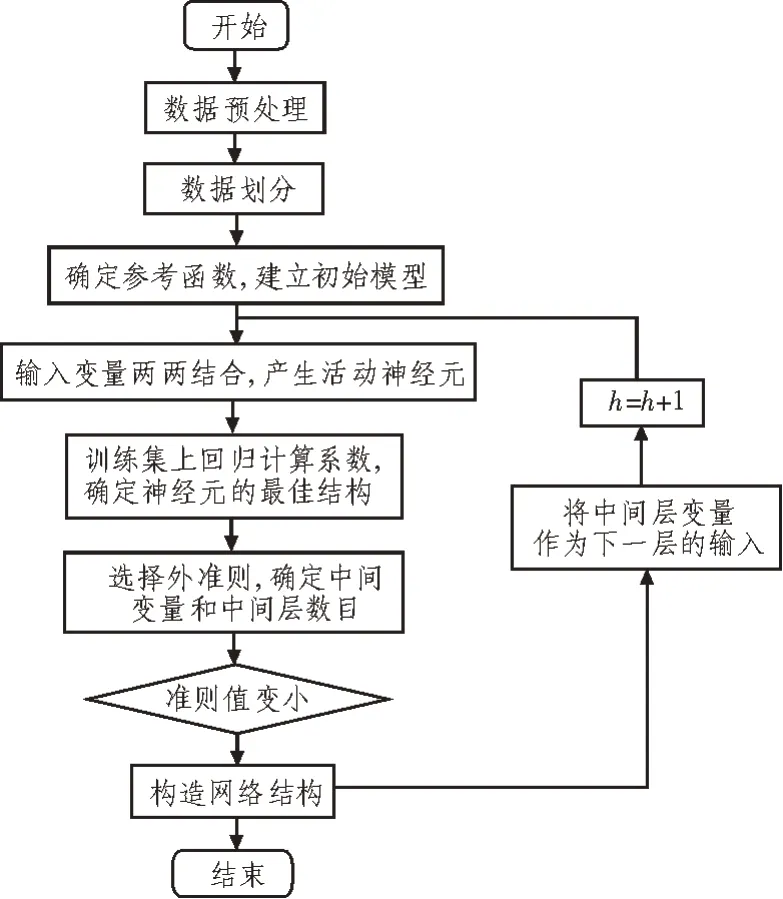
图4 算法流程图

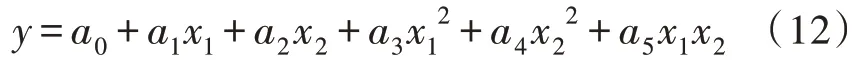
式（10）中，共包含5 个初始模型，初始模型的集合为式（13）。

随后，根据图4 将输入向量交叉并获得神经元，每个神经元均有一个函数序列，如式（14）所示。

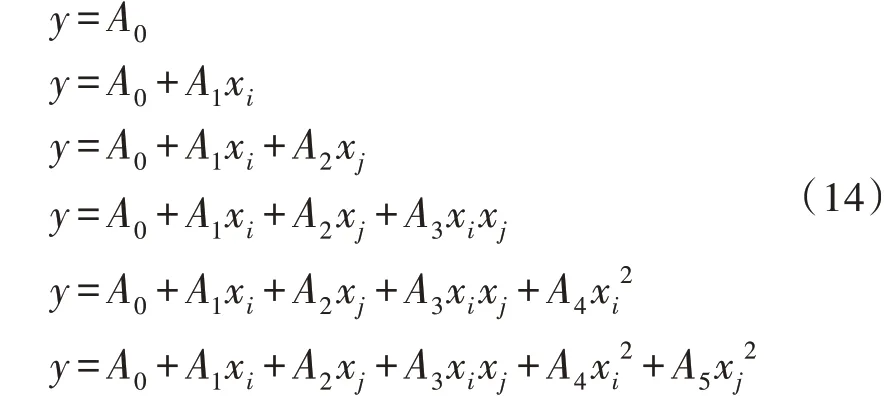
在此过程中，神经元的复杂性从y=A0开始递增，每一次递增的过程中，通过最小二乘法确定神经元的系数，判定标准为PESS，如式（15）所示。

2.2 仿真结果

根据图1 中的科技成果转移数据流程，共包含了H1、H2、H3、H4 4 个子系统。每个子系统均可用一个自组织网络进行描述，通过图4 的流程，可以得到4 个训练好的自组织网络。以H1 技术研发子系统为例，得到的网络模型如图5 所示。

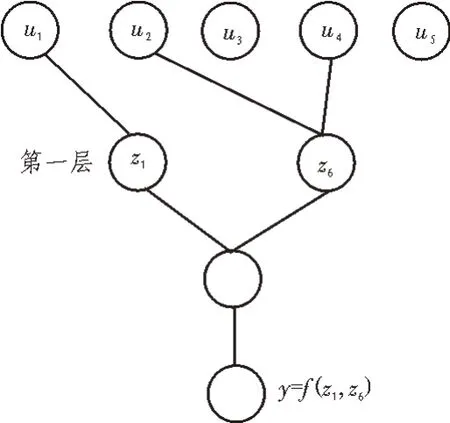
图5 H1网络参数结构

图5 所示技术研发子系统的网络参数，如表1所示。

表1 模型参数

使用得到的自组织网络与剩余的5 组测试数据进行网络性能的测试，为了更直观地评估模型性能，使用回归分析模型进行对比。表2 中给出了这5 个科技项目的实际社会收益、在回归分析法下及感应学习模型下的预测收益；表3 给出了两个模型的相对误差。

表2 科技项目转移效益预测结果 单位：亿元

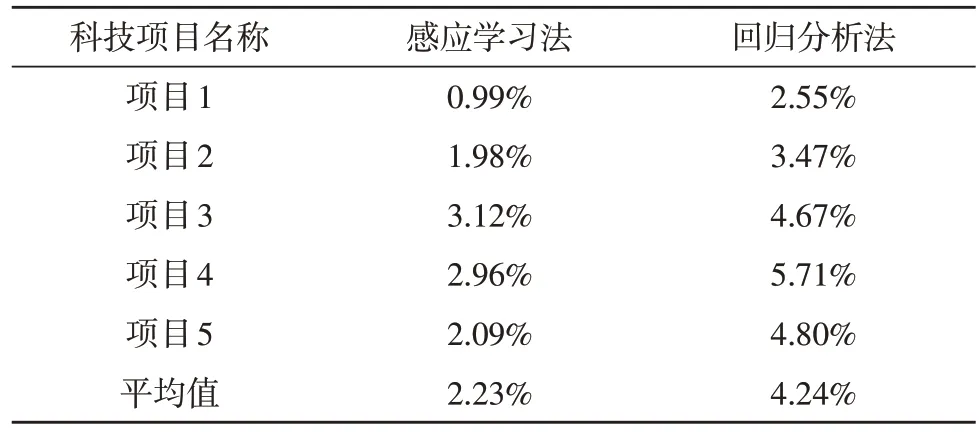
表3 算法误差统计

可以看出，该文提出的算法在该组数据下的平均相对误差为2.23%，相较于回归分析法的4.24%提升了约2%，误差的最大值为3.12%，而回归分析法的最大误差为5.71%。文中算法的误差在平均值附近波动较小，在针对某一项目进行预测时，更接近其真实值。但值得注意的是，回归分析法的预测结果大多小于实际的社会效益，数据具有较好的一致性。使用回归分析法进行预测时，只要将其预测值进行一定量的增加，即可接近实际的科技项目转移获得的社会收益。

3 结束语

该文对于科技成果的转移过程进行了抽象化的数学建模，该模型可以准确地描述转移过程中复杂的数据流向。该文模型的提出，方便了计算机智能化算法在科技成果转移领域的应用。在未来，科学地分析科技成果的转移效率对于科技项目立项、研发经费投入均具有重要的指导意义。