基于免疫克隆的图像稀疏分解算法研究

王 丽，王 威，刘勃妮

（西安航空学院电子工程学院，陕西西安 710077）

稀疏分解理论指出，信号在某些稀疏基上具有简洁的表达形式，降低了信号的传输压力，提高了信号的处理效率。在过完备库里寻找能够表示信号特征最优原子的过程，称为稀疏分解。高光谱图像(Hyperspectral Images,HSIs)[1]包含丰富的空间信息和光谱信息，其稀疏表示结果能够应用于图像分类、识别[2-6]等，可进一步推进高光谱遥感技术的发展。

文中首先给出谐波小波包字典的构造方法，然后介绍免疫克隆算法实现稀疏分解的过程，最后采用Matlab 软件进行仿真，对高光谱图像和一般图像进行稀疏分解，分析谐波小波包字典的稀疏表示能力。

1 谐波小波包字典

基于冗余字典的信号稀疏模型表示为：

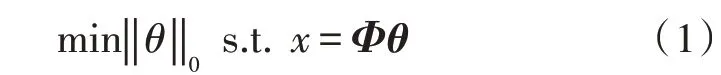
其中，x∈RN为原始信号，Φ∈RN×L为冗余字典，θ∈RL为稀疏系数向量。字典的每列元素称为原子。在稀疏分解中，需要解决两个问题：一是构造冗余字典，二是找到稀疏系数向量。

高光谱图像具有空间和谱间相关性，空间和谱间均存在冗余，具有稀疏性。但高光谱图像信号特征复杂，一般的冗余字典无法准确捕捉到信号特征。谐波小波包字典(Harmonic Wavelet Packet dictionary,HWP)[7-9]具有以下特点：1）具有信号频谱的盒型函数形式；2）表达形式简单清晰；3）具有正交性和对称性；4）实现过程简单。基于以上分析，选择谐波小波包字典作为高光谱图像的稀疏基，对其进行稀疏表示。

谐波小波包字典的频域表达式为：

其中，ω是频率，p和q是尺度参数，决定谐波小波的带宽。

对式（2）进行傅里叶逆变换，得到谐波小波包的时域表达式：

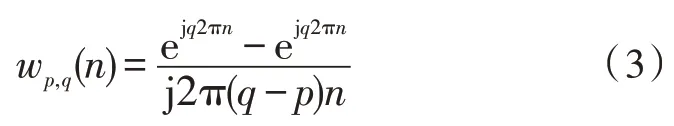
其中，n是时域变量。

对上述谐波小波进行位移变换，假定位移步长为v/(q-p)，v是位移参数，式（3）可变为：

式（5）表示的谐波小波的带宽为(q-p)2π，中心位置在v/(q-p)。与其他小波分解相似，当小波分解的层数越多时，小波分解的频域越窄，因此低频段的细化能力优于高频段。当分解层数指定后，谐波小波基函数的时宽、带宽均固定，无法与信号自适应匹配。为了解决此问题，采用谐波小波包的自适应分解方法[10]。

假设信号的最高频率为fh，若指定分解层数为s，则对应信号将被分解到2s个子频率段，每个频率段对应的信号带宽为：

由于谐波小波的带宽为(q-p)2π，故尺度参数p和q应满足：

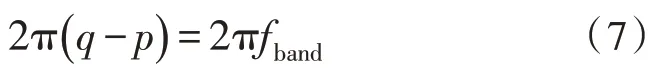
根据上述分析，将谐波小波的参数(p,q,v)对应到谐波小波包的参数(s,u,v)。假定信号长度为N，则分解层数s的范围是s=0,1,…,log2(N)-1。参数u是子带索引，其范围是u=0,1,…,2s-1。参数v是子带内小波系数的位置索引，其范围是v=0,1,…,N-1。则尺度参数p和q确定为：

通过这种自适应分解的方式，在每个分解层级上，均能在整个分析频域内得到高分辨率的分析结果。给定参数(s,u,v)，就能够得到一组谐波小波包字典，字典的原子个数为N(N-1)。

2 稀疏分解算法

正交匹配追踪(Orthogonal Matching Pursuit,OMP)[11]算法通过遍历冗余字典的所有原子，依次找出最优原子，实现信号的稀疏分解。当冗余字典的冗余较高时，正交匹配追踪算法的时间复杂度较高。文中借鉴生物种群的进化思想，引入免疫克隆概念，采用免疫克隆算法(Immune Clone Algorithm,ICA)[12]实现最优原子的搜索。与OMP 算法不同，ICA算法的全局搜索能力较强，通过模拟生物的免疫系统，采用克隆和记忆机制，实现生物个体的更新[13-14]。

在ICA 算法中，抗体是目标函数的一个可行解，抗原就是目标函数。与稀疏分解的目标函数相对应，每个抗体代表着从冗余字典中寻找到的原子。为了利用免疫克隆算法实现稀疏分解，首先，要产生一组初始的抗体；然后，利用亲和度函数计算抗体和抗原之间的亲和度。在抗体确定后，利用克隆、克隆变异和克隆选择3 个算子[15]，实现抗体的不断更新，随着进化过程的进行，找到最优原子并计算稀疏表示系数。

2.1 免疫克隆算法

2.1.1 初始化

1）初始抗体的产生

假定需要寻找的最优原子个数为K，则抗体表示为1×K的行向量，即a=(aa1,aa2,…,aaK)，其中aaK是集合[1,L]中的一个数字，代表冗余字典中的一个原子。种群包含M个抗体，表示为A=(a1,a2,…,aM)。

2）亲和度函数的设计

亲和度函数用于计算抗体和抗原的亲和度，即用于评价抗体代表的可行解的优劣。亲和度越高，表明抗体代表的可行解越优。设计的亲和度函数表示为：

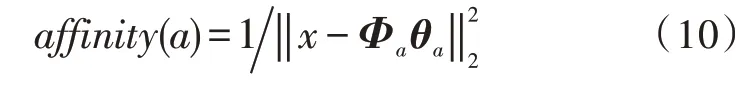
其中，Φa和θa是抗体a所对应的原子字典和稀疏系数向量。

2.1.2 初始化

1）克隆算子

每个抗体对应的克隆个数与其亲和度相关，定义为：

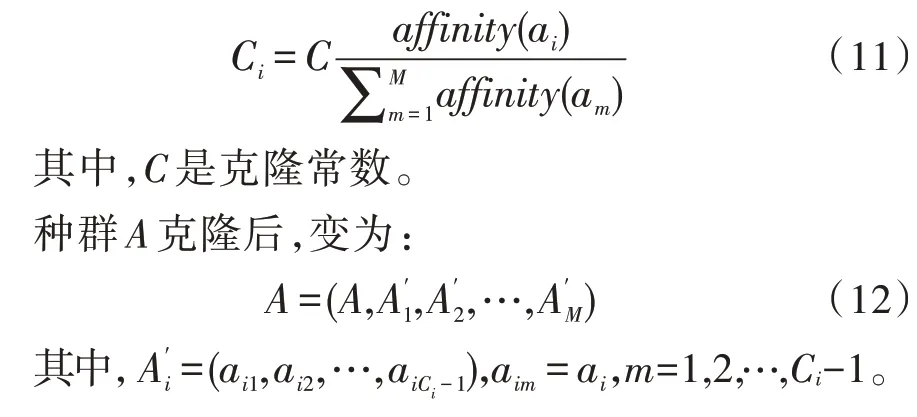
2）克隆变异算子

为了保留原始种群信息，只针对克隆个体进行变异操作。设定变异概率为Pm，对于抗体的每个元素，产生一个0 和1 之间的随机数r。如果r＜Pm，则对应的元素位置就替换为集合[1,L]中的任意数字，即变异为新的抗体。

3）克隆选择算子

假设某克隆变异后的抗体满足b=max{affinity(aim)|m=1,2,…,Ci-1}，并且满足：

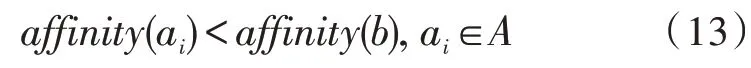
则用抗体b替代其父抗体ai，以更新种群。

通过克隆、变异、选择3 个算子操作后，初始群体将更新为具有更高亲和度的抗体。经过不断地进化后，找到最优个体abest，则稀疏系数表示为：

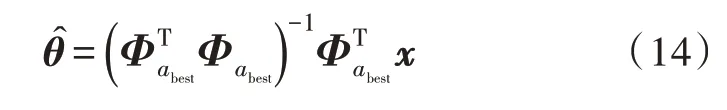
其中，Φabest表示最优抗体abest代表的原子字典。

2.2 实现流程

基于免疫克隆的稀疏分解算法实现流程图如图1 所示，其实现步骤如下：

Step 1 初始化：确定进化代数为t=1，产生初始抗体种群A1=(a1,a2,…,aM)。

Step 2 亲和度计算：利用式（10）计算种群At的抗体亲和度。

Step 3 克隆操作：利用式（11）计算每个抗体的克隆个数，根据式（12）获取克隆种群。

Step 4 克隆变异操作：产生随机数r，并与变异概率Pm进行比较，以获取变异种群。

Step 5 克隆选择操作：比较种群中所有抗体的亲和度，用变异种群的最优个体与父代抗体对比，采用式（13）获得种群At+1。

Step 6 判断停止条件：判断是否达到最大进化代数T，若达到则停止迭代，否则令t=t+1，重复执行Step2～Step6。

Step 7 选择最优抗体：计算种群AT的亲和度，选择具有最高亲和度的抗体为最优抗体abest。

Step 8 稀疏系数计算：采用式（14）计算稀疏系数。

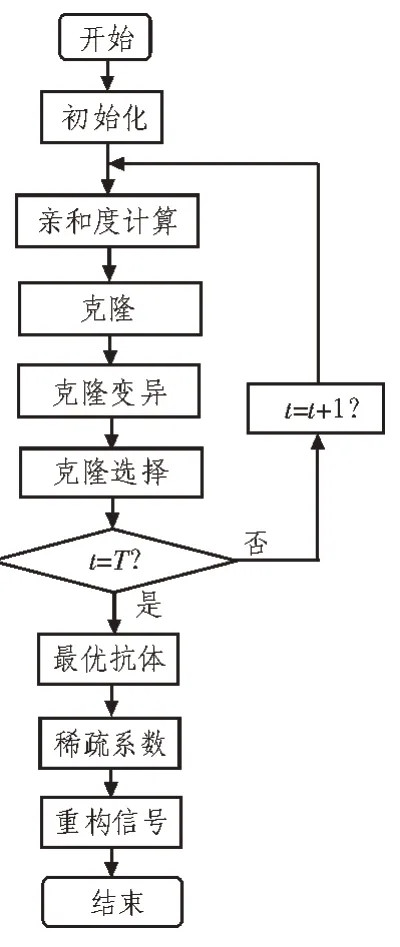
图1 稀疏分解算法流程图

重构信号表示为：

3 实验结果与分析

选择4 组图像对基于免疫克隆的稀疏分解算法进行验证，分析谐波小波字典的稀疏表示能力。第一、第二组图像是由美国的航空可见光/红外光成像光谱仪(Airborne Visible Infrared Imaging Spectrometer,AVIRIS) 采集得到的高光谱图像Cuprite1 和Cuprite2，两组数据集的波段数为224，图像大小均为614×512。去掉含噪波段和水汽吸收波段，可用波段数为188，第40 个波段图像如图2(a)和图2(b)所示。第三、第四组图像是一般的二维图像Lena 和Camaraman，图像大小均为256×256，如图2(c)和图2(d)所示。

图2 实验图像

因每个图像的空间像素较多，若对整幅图像进行稀疏表示，则冗余字典的冗余度太高，无法完成有效的稀疏表示，故对波段图像进行分块处理，分块大小为8，将每个块图像通过列优先的方式转换为一维向量，然后进行稀疏分解，分解后再恢复为图像块形式，完成每个图像的稀疏表示。对高光谱图像进行空间裁切，将图像裁切为256×256，波段数仍为188。

选择Gabor 字典[16]与构造的HWP 字典进行比较，以分析HWP 字典对高光谱图像的稀疏表示能力，利用ICA 稀疏分解算法对4 组高光谱图像进行稀疏分解。以重构图像是原始图像和噪声图像的叠加为基础，定义原始图像的最大灰度值与噪声图像的标准均方差的比值为峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)[17]，并以dB 作为峰值信噪比的单位。每个波段图像的峰值信噪比定义为：

利用ICA 搜索得到的32 个原子构成重构图像，在进化过程中，种群个数设置为M=10，克隆常数为C=15，变异概率为Pm=0.2，最大进化代数为T=20。利用重构图像和原始图像之间的峰值信噪比对字典的稀疏表示能力进行评价，4 组图像的重构峰值信噪比见表1。无论是高光谱图像还是一般图像，在搜索的原子数相同的条件下，HWP 字典均能得到优于Gabor 字典的结果，两者的平均峰值信噪比之差最高能达到4.90 dB。特别是，对于高光谱图像来说，HWP字典能够得到较高的重构峰值信噪比，说明构造的谐波小波包字典更能表示高光谱图像的复杂信号。

Cuprite1 场景、Lena 场景的重构图像对比如图3和图4 所示。从视觉效果上看，与原始图像相比，利用Gabor 字典得到的重构图像的细节更为完整。利用Gabor 字典得到的重构图像的块效应比较明显，而谐波小波字典得到的重构图像则弱化了块效应的影响，重构图像更加光滑。

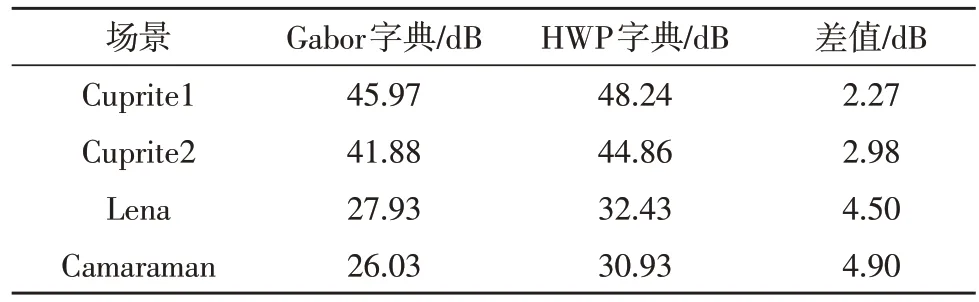
表1 利用两种字典得到的峰值信噪比

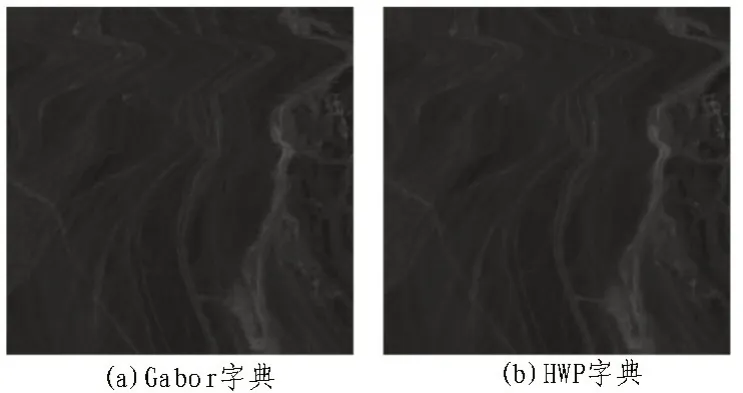
图3 场景Cuprite1的重构图像对比

图4 场景Lena的重构图像对比

4 结论

文中对基于免疫克隆的图像稀疏分解算法进行了研究，首先构造了用于表示复杂图像的谐波小波包字典，然后研究了基于免疫克隆思想的稀疏分解算法，包括初始种群的产生、亲和度函数设计以及克隆算子、免疫算子和选择算子的设计等，并给出了算法的实现过程。采用基于免疫克隆的稀疏分解算法对高光谱图像和一般二维图像进行仿真实验，实验结果表明，与Gabor 字典相比，HWP 字典对高光谱图像的稀疏表示能力更强，获得的重构图像峰值信噪比更高。如何降低块效应对重构图像的影响是进一步研究的方向。