基于演化聚类算法的电力系统暂态负荷同步预测

荆林国，荆仲毅，张韶晶，张韶颖

（1.国网山东省电力公司滨州供电公司，山东 滨州 256610；2.山东科技大学，山东青岛 266590）

电力系统由大量非线性元件组成，是一个非常复杂的动态系统，其暂态负荷特性是学者们热衷讨论的话题之一[1-2]。目前，通常采用基于时域变换法的电力系统暂态负荷同步预测方法[3]，时域变换法的原理是将电力系统中各个元件模型根据元件间的拓扑关系形成全系统数值计算模型，从而对电力系统暂态负荷进行预测。其在计算时，选择电力系统的稳态工况为计算初值，求解发生故障后的数值解，并根据发电机转子摇摆曲线判别系统在遭遇故障后暂态的稳定性。但是，随着发电量的增加，各个输电工程的高压电流也不断增加，并依据我国电力发展的“十三五”规划，到2020 年全国风电和光伏发电的总装机容量将达到2.1 亿kW 和1.1 亿kW 以上[4]。在该背景下，逐渐改变了传统的电力网络拓扑结构，补充大量的电力电子器件，增加了电力系统的动态特性。传统的基于时域变换法的电力系统暂态负荷同步预测方法已经不适用于电力系统暂态负荷同步预测，逐渐出现预测准确度低的情况。为此，设计一种基于演化聚类算法的电力系统暂态负荷同步预测方法，演化聚类算法可处理随着时间变化而变化的数据，在每一个新的时刻都能够准确地对数据聚类划分。因此，将其应用到电力系统暂态负荷同步预测中，提高电力系统同步预测的准确性。

1 暂态负荷数据修正

电力负荷预测工作较大程度上取决于所收集到的历史数据情况，准确、完整的历史数据可提高预测结果的精度。因此，在电力系统暂态负荷数据预测时，采集并修正负荷数据中缺损的部分是极其重要的。若由于历史原因或者管理部门疏忽的原因造成数据缺失的现象，即为数据空缺，采用简单的BP 神经网络对其补缺。BP 神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，将其输入与输出值定为该时间与对应时间内的负荷值[5]。负荷值作为输入来训练BP 网络，构造成一个完整的BP网络。将补充数据的时间作为BP 网络的输入变量引入训练好的BP 网络中，从而得到该时间负荷值的补全值。对于偶然因素造成的伪数据现象，对其进行修正，修正公式如式（1）所示：

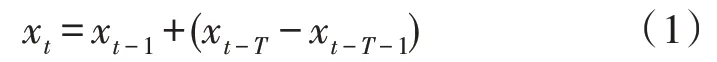
式（1）中，xt代表t时刻的负荷值，xt-1为t-1时刻的负荷值，T代表日负荷的采样点数，xt-T、xt-T-1分别代表t-T时刻与t-T-1 时刻的负荷值。

根据上述过程完成采集数据的修正，由于采集到的静态历史数据集不能反映出负荷数据变化的规律，因此，引入演化聚类算法概念，在每一个新的数据到达后，对于这批数据进行正确的聚类划分。设置一组k个聚类中心，每组聚类中的初始值是随机产生的，即：

依据聚类算法，可真实准确地反映电力系统在每一时刻的负荷数据分布，确保聚类结果平滑，保证当前时刻的数据聚类结果与前一时刻的聚类结果尽可能相似。

2 电压相量距离计算

依据上述修正后的电力系统暂态负荷数据，对电压向量距离进行计算。根据当前电网的运行方式，若电网发生故障，则发电机相角也会增加，母线电压之间的夹角也会发生变化，因此计算电压相量距离。电压向量图如图1 所示。

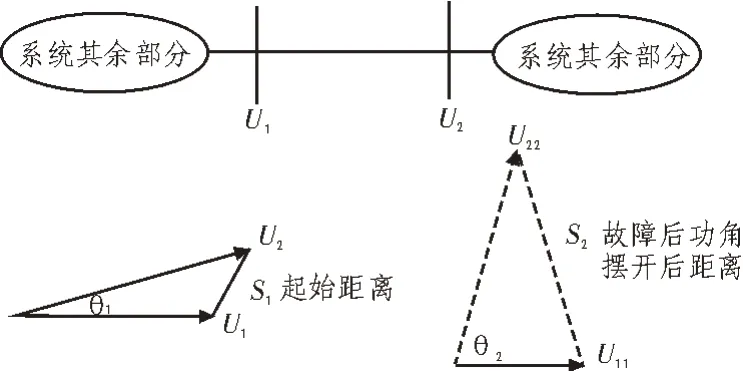
图1 电压相量图

图1 中，U1、U2分别代表系统稳定状态下母线1和2 的电压相量；U11、U22分别代表系统发生故障后母线1 和2 的电压向量；θ1、θ2分别代表系统的稳定状态[6]和系统发生故障后母线1 和2 电压相量的夹角；S1代表故障前1 和2 母线电压的相量差，S2代表故障后1 和2 母线电压的相量差。

考虑到电网中的节点较多，若对电压相量距离进行开方运算[7]，则会增加计算量，因此，定义S为电压相量距离的平方，则电压相量距离计算公式如式（3）所示：

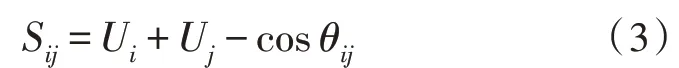
式（3）中，Sij代表母线i与母线j之间连接线路的电压相量距离的平方；Ui和Uj分别代表电力系统稳定状态下母线i和j的电压值，cosθij代表母线i和j电压相量之间的夹角。

由于在电力系统发生故障后，电压相量距离会产生一定的突变量[8]，因此，对上述计算得到的电压向量距离做分段处理。每进行一次计算后，都重新计算距离量，则支路电压相量距离变化量[9]为：

式（4）中，B代表支路电压相量距离变化量，Sit代表电力系统发生故障t时刻i支路的电压相量距离，w初始时刻的电压相量值。

美国著名商业调查公司民茨公司(Mintz Group)调查员兰德尔·菲利普斯(Randal Philips)认为，中国提出的“一带一路”倡议是对奥巴马政府“亚太再平衡战略”，特别是TPP经济倡议的回应，通过这一计划提供有别于美国的规则与机制，而该地区相对欠缺的基础设施投资恰好提供了通向这一替代计划的便捷之路。而且，在中国领导人看来，“一带一路”倡议是提升中国国际地位和形象的理想的政治经济平台，无论在规模还是目标上都要超越二战后的美国马歇尔计划。[19]

通过电压相量距离计算能够得到电力系统中支路暂态势能的等效映射关系[10]，即得到与电网中的薄弱断面之间的关系。

3 暂态负荷同步预测

根据上述得到的电压相量距离判断相应时间内的电网薄弱断面，针对每个输电断面，采用下述公式计算电网中各个发电机在该断面的综合参与因子，通过筛选得到该输电断面的关键故障集中的故障数[11]，计算公式如式（5）所示：

式（5）中，F代表当前输电断面的关键故障集中的故障数，Ka、Gn分别代表第a个和第n个发电机参与因子，V为筛选后的关键故障因子。

由于每个输电系统中都包含两个输电断面，因此，通过上述公式可以计算另一个输电断面中的故障数，得到两个输电断面的关联性关系[12]。若这两个输电断面的故障数相同，则代表电网运行状态变化对两个输电断面影响方向一致；若不相同，则代表运行状态对两个输电断面的影响方向相反，代表其中一个输电断面的暂态安全稳定水平[13]与另一个断面的暂态负荷稳定水平之间不存在关联性。因此，通过上述计算得知电网中输电断面的暂态负荷信息[14]，并能够反映出电网中各个输电断面的暂态负荷关联程度。

由于上述计算是针对电网中各个输电断面[15]中的各个故障集进行的电力系统暂态负荷同步预测，因此，仅采用了较小的计算量就得到了预测结果。

为保证输出的结果不被干扰，将其存在数据库中，数据库结构如图2 所示。

4 仿真实验

实验目的是验证基于演化聚类算法的电力系统暂态负荷同步预测方法在实际应用中的性能，将其得到的结果、基于时域变换法的预测结果与实际结果进行对比，验证所提方法的预测性能。

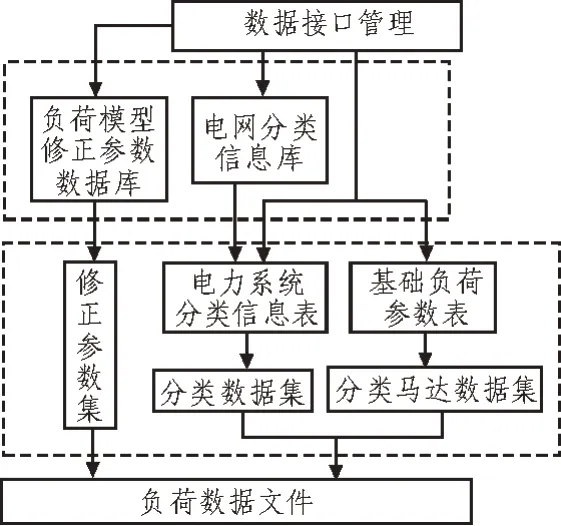
图2 预测结果输出数据库

该实验采用光伏发电系统，因为光伏发电系统中动态特性较强，目的是增加实验的对比性。

4.1 实验样本准备

为增加实验结果的对比性，在实验电网中设置干扰项，实验具体步骤如下所示：

第一步，选取光伏发电系统的正常运行方式为基准各个负荷水平在95%～105%之间；

第二步，在某条线路的某侧添加故障，在0.2 s 时添加故障，为故障的开始时刻，在0.3 s 清除发电机组故障。

当系统发生故障后，光伏与正常的电压、功率差异较大，因此，以光伏发电系统在故障开始和清除时刻的光伏端口电压与功率的变化情况为判定预测方法准确性的依据。

4.2 实验结果

实验中，已知光伏发电系统在故障开始和消除时刻的光伏端口电压与功率的变化情况，将两种算法预测到的值与实际值对比，对比结果如图3所示。

由图3 可知，在故障开始与消除时刻，光伏端口电压与功率发生变化，并得到以下结论：

1）由光伏有功功率曲线变化图可知，实际的光伏有功功率变化曲线中，光伏有功功率在故障开始时功率速降，在故障中有功功率有增长现象，在故障消除后达到最大值时开始降低达到稳定值。将该设计预测方法得到的值与其对比可知，在故障消除后，预测到的值与实际曲线值相差较小，在达到最大值后功率值出现小幅波动，与实际值有一些差距。而基于时域变换预测方法得到的值在故障消除后的功率与实际功率曲线相差较大，并在达到最大值后，功率呈下降趋势，与实际值不符。

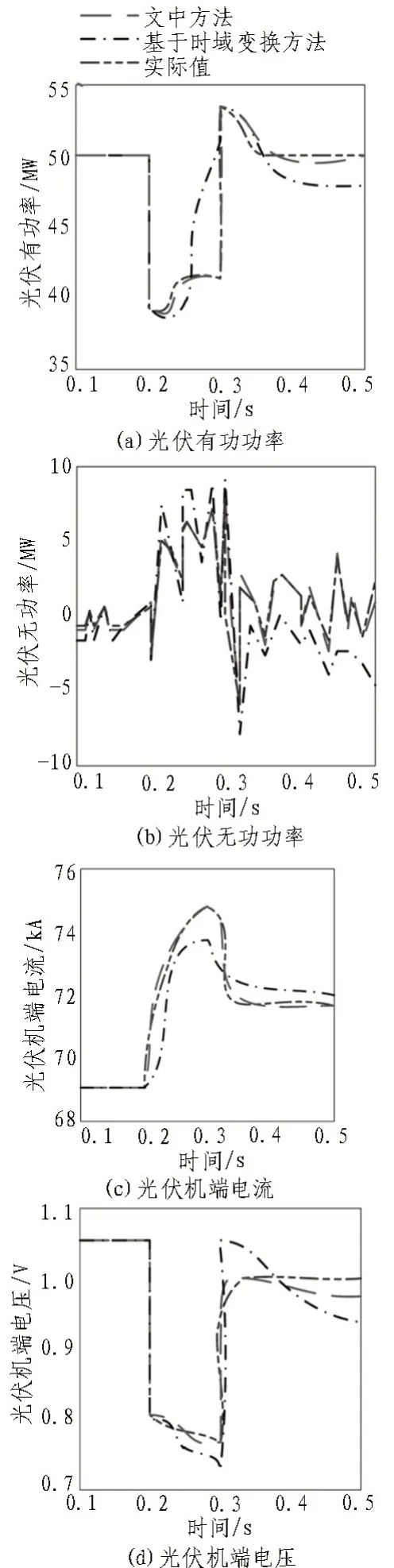
图3 光伏发电机端电压和功率变化曲线

2）由光伏无功功率可知，在实际情况中，光伏无功功率受故障影响较小，在故障发生的初始时刻与结束时刻无功功率变化幅度较小。该设计预测方法得到的预测值曲线波动幅度与实际值相差小，变化幅度相对较小，而基于时域变换预测方法得到的值在故障开始后无功功率值出现3 次较大的波动，并且在故障消除后，波动幅值较大，与实际值具有一定的差距。

3）由光伏机端电流曲线值与光伏机端电压值可知，电流及电压在故障初始时刻与清除时刻变化较大，与实际值的最大误差为0.025 V，其他时刻为稳定状态。文中设计方法得到的电流曲线值与光伏机端的实际值基本保持一致。由基于时域变换方法预测结果和实际结果对比可知，基于时域变换方法得到的值在故障初始与清除时刻电压、电流值变化大外，其他时刻电压、电流值变化也较大。

综上所述，由文中设计的预测方法得到的光伏发电机端电压和功率变化曲线与实际曲线相差较小，基于时域变换方法的预测结果与实际结果相差较大，因此可证明，文中设计的预测方法比传统方法预测准确度高。

5 结束语

为了提高电力系统的运行稳定性，提出暂态负荷同步预测方法，采用演化聚类算法对修正后的历史数据完成电力负荷计算。实验结果表明，所提方法的预测结果与实际结果基本一致，充分说明所提方法能够准确实现电力系统暂态负荷的同步预测。暂态负荷评估的目的是为电力系统制定预防控制措施提供信息支撑，因此，有必要在文中研究成果的基础上，采用更大的系统进行验证，并考虑系统多摆失稳现象，从而进一步提高暂态负荷预测准确性。