一种高压断路器机械寿命预测算法研究
王俊波,李国伟,唐琪,刘崧,洪贞贤
(广东电网有限责任公司佛山供电局,广东佛山 528000)
高压断路器作为电力系统三大器之一,有着举足重轻的地位[1-5]。每一种电力设备都有它的运行寿命,高压断路器的运行寿命通常为20~40 年。随着服役时间的增加,高压断路器某些部件会不断老化,甚至损坏,如机械机构的磨损、触头的磨损等。如何快速、准确地对服役中的高压断路器寿命进行分析、诊断乃至预测,是生产厂商、科研院校、电力部门一直关注的问题,对这些部分已付出了大量的研究精力,也得到了一些有益的研究成果[6-8]。静态机械寿命预测是目前最直接的、采用最多的,也是最受到认可的方法,即读取高压断路器动作次数并记录在案,依次累加,获得分、合闸动作的总次数。已知原始机械寿命动作次数,即可算得剩余寿命,比如广东电网采用动作次数达到一定值后更换极柱的运维策略,在35 kV 无功补偿用高压断路器上取得了良好的效果。然而,静态机械寿命为高压断路器理论上的寿命,无法体现高压断路器运行工况,例如高低温环境、灰尘、湿度、开断电流、过电压累计效应等。
1 算法基础
各行各业产品或者设备的大量统计数据表明,产品或者设备的失效率和服役时间满足浴盆曲线的关系。如图1 所示,λ为失效率,t为服役时间,浴盆曲线说明整个寿命周期会明显分为3 个典型阶段:第一阶段是投运初期,这一阶段失效率高且会随着服役时间的增加迅速下降,失效原因多是工艺缺陷等产品质量问题;第二阶段是随机失效期,这是产品或者设备的黄金工作周期,失效率非常低且非常稳定,失效原因多是遭受了外来偶发的不可抗力;第三阶段是耗损失效期,失效率随着服役时间的增加会明显增大,失效原因是设备疲劳、老化等[9-15]。
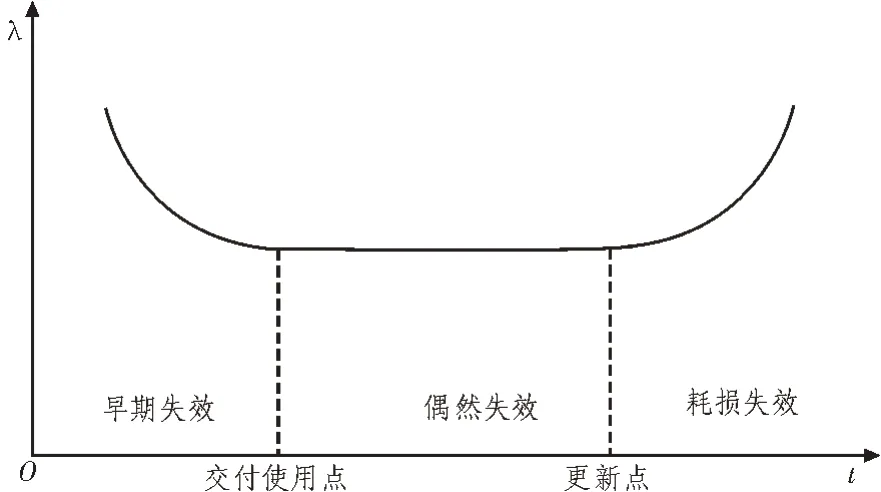
图1 浴盆曲线
首先分析高压断路器的分、合闸过程。合闸过程:合闸脱扣器带电—合闸脱扣器动作—完成合闸脱扣—合闸弹簧释放能量—通过凸轮及传动部件(例如四连杆)—高压断路器的传动部件(拐臂和绝缘拉杆,钢拉杆)—带动触头系统合闸动作,触头系统按一定的分、合闸速度动作—弧触头接触为合闸时间的节点。分闸过程:分闸脱扣器带电—分闸脱扣器动作—完成分闸脱扣—分闸弹簧释放能量—通过传动部件(例如四连杆)—断路器的传动部件(拐臂和绝缘拉杆,钢拉杆)动作—带动触头系统分闸动作—主触头分离—弧触头分离(触头开始运动到弧触头分离时间称为超行程时间)。
通过对以上分、合闸过程的分析,可以清楚地看出,合闸时间包括合闸脱扣器带电时间、合闸脱扣器动作时间、触头的合闸时间,即合闸速度的大小将影响合闸时间的长短;分闸时间包括分闸脱扣器带电时间、分闸脱扣器动作时间、触头超行程时间。
高压断路器的机械结构相当复杂,由多个部件相互配合,在分、合闸动作过程中不可避免地存在磨损、变形,甚至沿海地区的高湿度、高盐雾也会引起线圈霉变等产生负载应力,如果针对每一个机械部件做研究是显然办不到的,但上述原因造成运动系统的卡涩是必然的,也就是说,分、合闸时间变长是这些隐形影响因素的显性化。再则,由于分闸时间包括超行程阶段,主触头和弧触头(尤其是弧触头)在开断电流后,触头表面烧蚀,其表面的光洁度下降,运动摩擦阻力增加,引起分闸时间增加。因此,分、合闸时间在整个运行寿命周期内应是一个缓慢退化的过程。当分、合闸时间值退化至超出技术条件要求时,认为设备寿命终止,这是利用分、合闸时间与动作次数的内在关联关系去预测机械寿命的理论基础[16-20]。
2 算法流程设计
针对高压断路器机械寿命预测方法开展流程设计,包括以下步骤:通过指数分布模型描述高压断路器损耗失效期的失效率,并采用最小二乘法拟合多项式模型来代替指数分布模型;统计高压断路器的分闸次数、分闸时间、合闸次数、合闸时间的历史数据,得到m组数据(xi,yi);根据多项式模型,得到m组数据的总方差,根据方差最小的点整理得到范德蒙德矩阵,并进行求解;将求解得到的数据代入多项式模型,求出分、合闸时间的拟合曲线;绘出高压断路器分闸时间劣化曲线和合闸时间劣化曲线,根据高压断路器的分、合闸次数,即可求出高压断路器的运行机械寿命次数,流程如图2 所示。
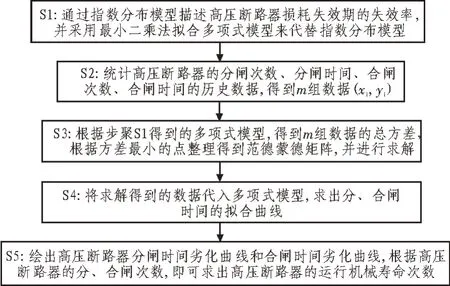
图2 算法流程
3 算法实现
高压断路器的分、合闸时间与开断次数有着明显的相关性,分、合闸时间在一定程度上反映了断路器的机械寿命。通过对历史数据的拟合,可以预测分、合闸时间和开断次数的关系。
对于高压断路器的机械寿命预测,更关注随机失效期和损耗失效期的转折点,这对于进入损耗失效期的高压断路器差异化的运维策略极为关键。失效率λ和服役时间t的关系如式(1)所示。
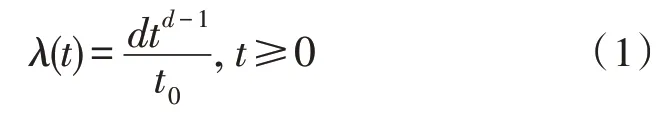
其中,d,t0是两个正参数,当d=1 时,λ(t)是常数,对应指数分布,因此采取指数分布模型可以较好地刻画处于随机失效期的高压断路器的机械特性,因此通过指数分布模型描述高压断路器损耗失效期的失效率。根据泰勒定理可知,指数模型又可以展开为多项式模型,如式(2)所示。
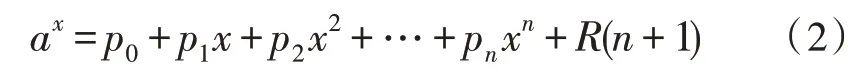
其中,p0,p1,p2,…,pn是常数,R(n+1) 为n+1阶截断误差。
采用最小二乘法拟合多项式模型来等效代替指数分布模型,拟合多项式如式(3)所示。
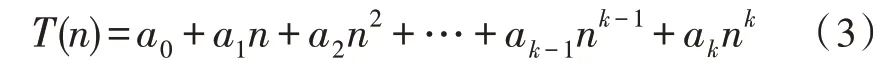
其中,n是高压断路器分(或者合)闸次数,T(n)是预测的高压断路器第n次分(或者合)闸时,其分(或者合)闸时间,a0,a1,a2,…,ak是未知常数。
假设第n=xi次开断时,测得的分闸时间为yi,其中i=1,2,3…m。此时,m个样本的总方差如式(4)所示。
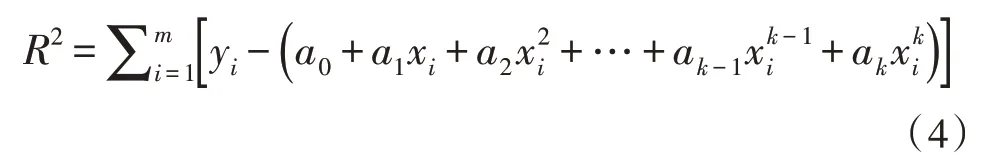
使得样本总方差最小的a0,a1,a2,…,ak的值就是最佳拟合曲线的解,式(4)可以看作是函数R2(a0,a1,a2…ak)方差最小的点,即函数的驻点,如式(5)所示。

式(7)是一个范德蒙德矩阵,由于x1,x2,…,xm互不相等,所以上述矩阵方程存在唯一解,解为a0,a1,a2…ak,将求解得到的a0,a1,a2,…,ak代入式(3)的多项式模型,得到分(或者合)闸时间与动作次数的拟合曲线。
4 实验验证
选取一台A 厂家生产的额定电压为42 kV 的无功补偿用高压断路器,开展多次负荷开断实验,模拟实际运行工况。使用Matlab编程实现第2节提出的高压断路器机械寿命预测方法,通过统计分、合闸时间进行寿命预测算法验证,以分闸为例,统计分析结果如图3所示。
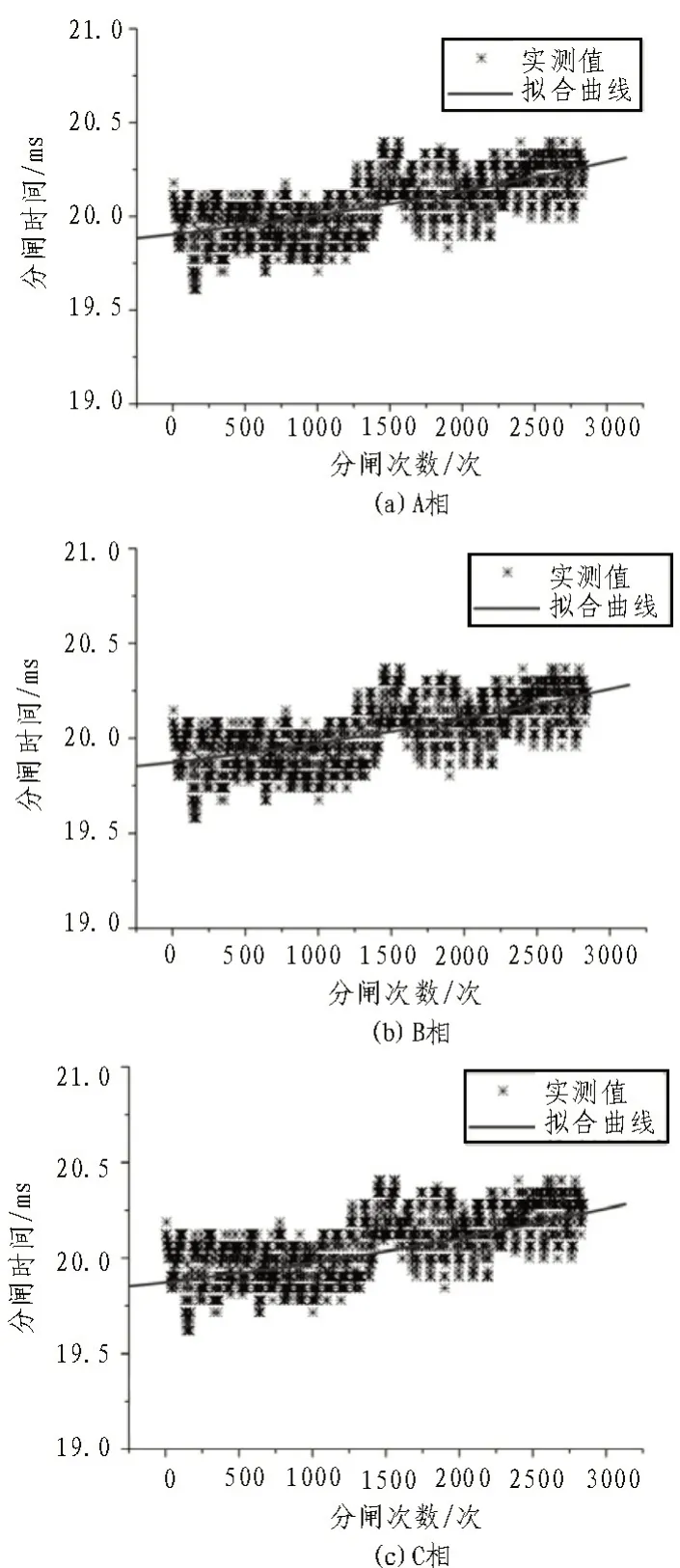
图3 分闸时间统计分析
对比图3(a)、(b)、(c)可以看出,实验用高压断路器三相之间横向对比差异很小,分闸时间均稳定分布在20.5 ms 以下,并且统计规律表现出极强的一致性,这证明三相产品虽存在个体差异,但其极柱结构、触头材质、工艺条件、运行工况等内、外部因素基本一致,这是符合生产应用实际需求的。从图3 拟合曲线可以得出两条重要结论:
1)在高压断路器大约动作5 000 次之后分闸时间才会超过厂家规定值,所以预测其机械寿命为5 000次,这与厂家规定的7 000次的理论寿命有差异。
2)高压断路器三相分闸时间均未出现阶跃式升高,但总体趋势上是在增大的,属于机械性能的正常退化。
查阅出厂文件可知,该型号高压断路器分闸时间出厂规定值要求不得超过20.8 ms,按照广东电网运维策略,该组高压断路器已经达到更换极柱的条件。因此,运维策略较为粗放,存在一刀切的嫌疑,差异化运维策略的颗粒度仍存在细化的空间。
5 结论
按照提出的机械寿命预测算法,以分闸次数为横坐标,以分闸时间为纵坐标绘制高压断路器分闸时间劣化曲线,以合闸次数为横坐标、以合闸时间为纵坐标绘制高压断路器合闸时间劣化曲线。再进一步地,根据高压断路器的出厂技术要求,确定高压断路器的劣化极限,所述的劣化极限包括分闸时间上限、合闸时间上限,若达到这个劣化极限,则高压断路器要停止运行。该算法具备以下优点:
1)摒弃了现有预测方法给出的要么健康,要么故障的二值化判断方法,将高压断路器故障演变过程真实地反映出来,可以对影响机械寿命的潜伏性故障做出预判。
2)由于算法采用的最小二乘法拟合是基于高压断路器实际运行数据的自学习,因此在将隐形影响因素显性化的同时实现了高压断路器机械寿命的差异化预测。
综上所述,高压断路器分、合闸时间是机械性能最为直观的反映,它既代表了高压断路器当前的健康状态,又反映了高压断路器自服役之后健康状态的演变过程,本身即是一种离散型的在线监测数据,但单一时间断面的数据不能客观反映高压断路器的健康状态,因此采用一定的算法开展数据挖掘,将离散数据中隐藏的趋势显性化,这对于高压断路器机械寿命预测是非常实用的。建议各个供电部门有意识地积累并标准化历史数据,在应用过程中可以不断优化算法,使得预测精度越来越高,从而有效指导高压断路器差异化运维策略的制定。

