电动自卸车轮边驱动电机输出转矩控制分析
崔丹丹,崔高伟
(1.中原工学院信息商务学院,河南 郑州 450007;2.上海航天控制技术研究所,上海201109)
1 引言
电传动车辆高效的传递模式,被广泛应用在各类矿山开采运输中。此类车辆在实际使用过程中会有这样的现象:由于输出电机转矩波动,造成部分工况车辆存在抖动现象,而这将造成系统部分单元磨损加剧而影响寿命[1]。电传动车辆的常常工作在这些工况,所以对于此类车辆的设计者来讲转矩波动问题不可不考虑。
国内外学者取得一定的成果:文献[2]提出模型跟踪控制,将车辆动力学看作一个可变的惯量系统;文献[3]通过实时测试路面滑移率,将其作为控制模型输入,对车辆进行控制;文献[4]提出通过控制附着系数与滑移率的斜率来保证车辆稳定运行;文献[5]利用驱动电机估计出最大可传递转矩输出,通过直接限制转矩参考值而防止车辆打滑。
针对电传动车辆轮边电机输出转矩波动问题进行分析,搭建轮边电机矢量控制模型,从控制模型入手研究影响转矩波动的原因以及应对的方法,基于Simulink 搭建动力传递系统模型,并对轮边电机驱动及转矩控制模块进行封装,基于Pharlap 系统,利用NI PXI 做目标机,对模型进行不同工况实时仿真,验证所提出控制方法的有效性。
2 轮边电机控制模型
2.1 电机数学模型
在静止坐标系[6],电机相关方程可写作:
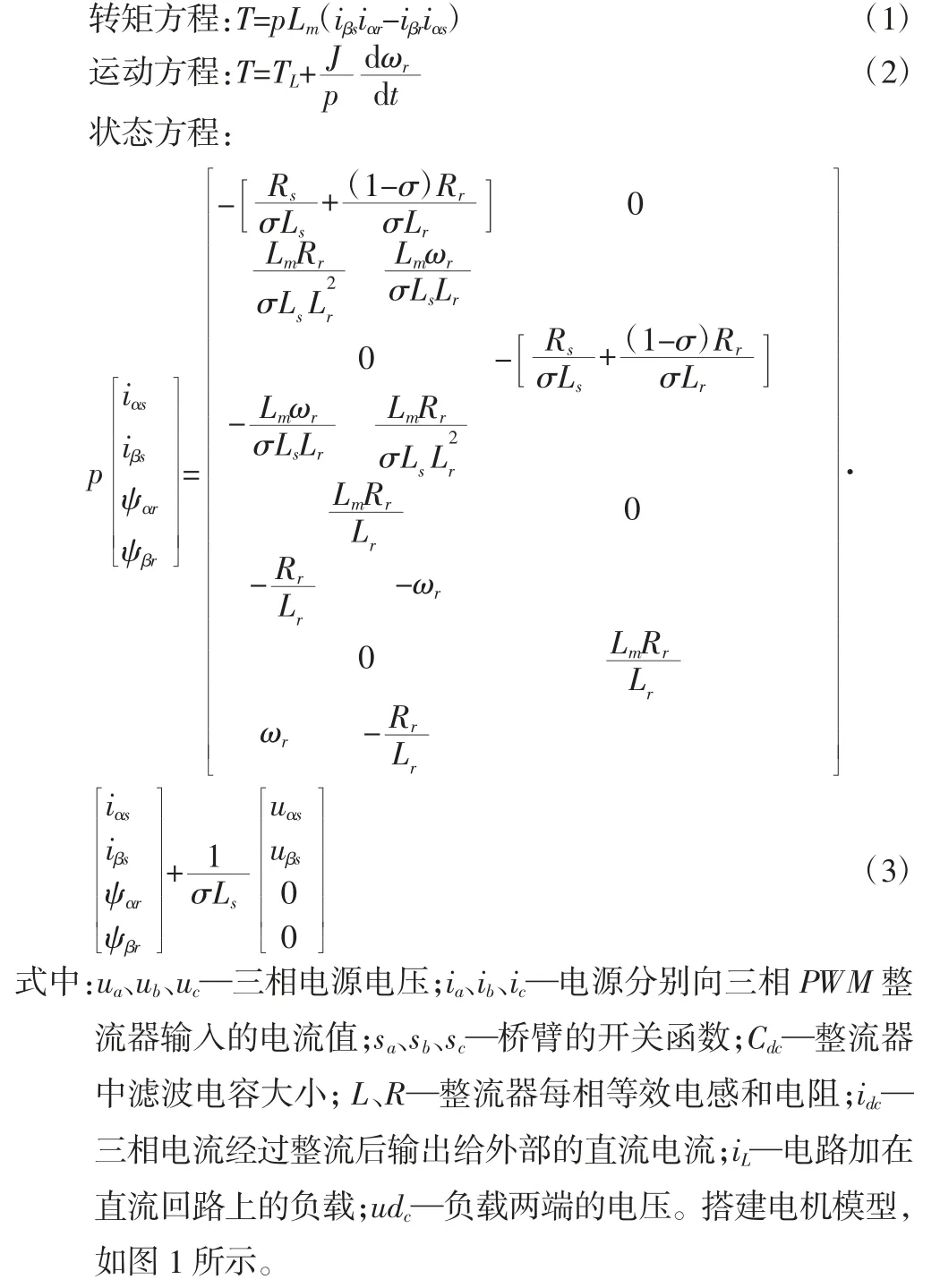
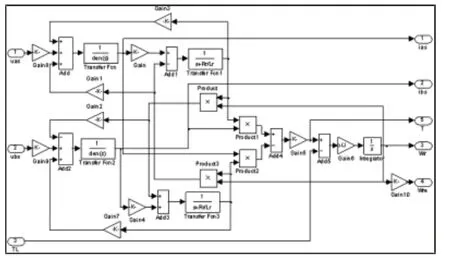
图1 电机模型Fig.1 Motor Model
2.2 电机矢量控制模型
矢量控制系统的原理,如图2 所示。
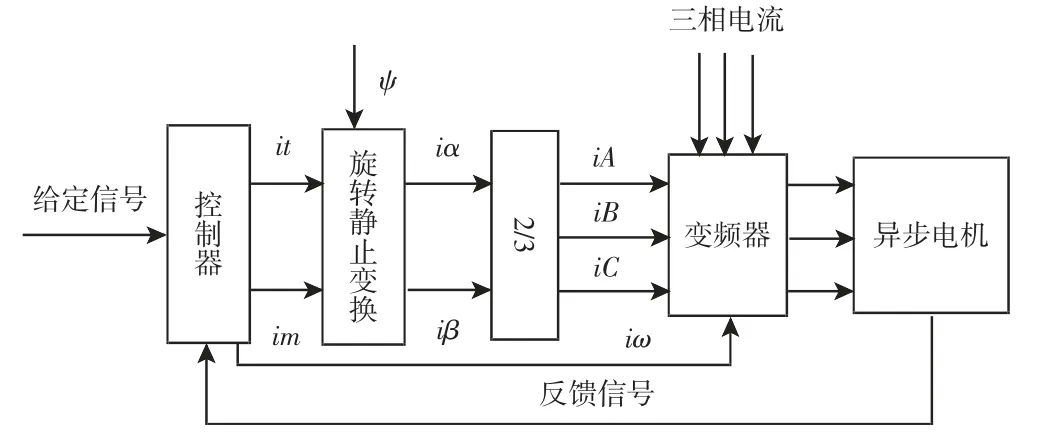
图2 矢量控制原理示意图Fig.2 Schematic Diagram of the Principle of Vector Control
图2 中所示,信号经过直流调速系统控制器,得到磁链电流和电枢电流,经过坐标变化获得两相电流,之后通过2/3 变换模块得到静止三项坐标系上的电流iA、iB、iC,使其与频率信号加到变频器上,即可得到异步电机调速所需的三相电流,将此电流输入异步电机则达到控制异步电机的目的。
根据转子定向矢量控制[7],则电机控制模型写作:

根据此可搭建出模型,如图3 所示。

图3 电机控制模型Fig.3 Motor Control Model
2.3 轮边电机负载合成转矩
电机的输出轴与轮边减速器太阳轮相连,在轮边减速器齿圈的带动下轮胎转动,并接收地面传来的力[8]。由此,可以确定,作用在电机输出轴的力矩有如下几种:轮胎系统的惯性力矩,地面附着力对电机反作用力矩,滚动阻力矩。

3 输出转矩波动及控制
3.1 转矩波动原因分析
对电机输出控制模型进行加载,200Nm 的负载,目标速度20r/s 的结果,如图4 所示。
由图4 可知,结果稳定且符合设计要求,当转矩有上下50 的波动。分析可知,引起电动轮转矩波动的影响因素如下:
(1)转矩给定不稳定
当转矩信号有偏差和干扰,这就使得信号发生扰动造成转矩的波动[9]。这个问题的解决办法是让信号经过滤波器或者给油门和电流检测信号线加屏蔽。

图4 带负载运行结果Fig.4 With the Load Operation Results
(2)电流和转速等反馈信号检测误差较大
此类误差对元件在电磁干扰下会对结果造成影响。此外,由于温度变化或电压不稳定时,静态工作点发生变化,如零点漂移,导致检测误差变大。这种情况需要进行补偿和调制两种手段来解决[10]。
(3)电流换向
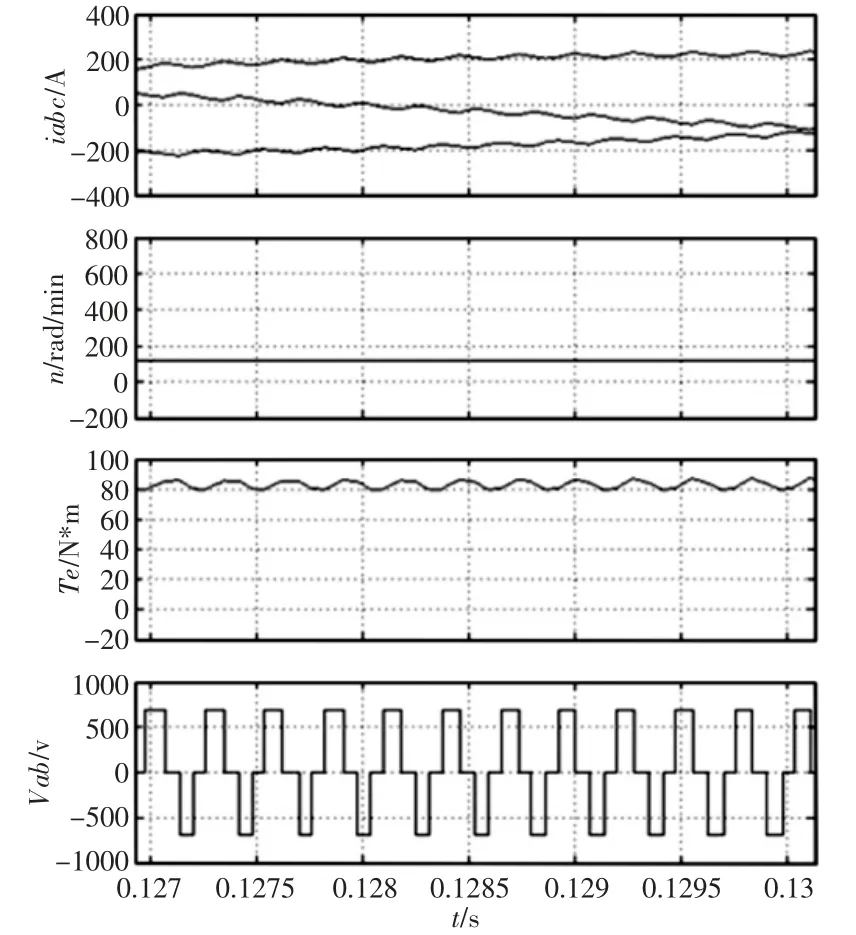
图5 转矩波动Fig.5 Torque Fluctuations
由于输入的是三相交流电,电流换向不免引起转矩的脉动。在电机调速过程中应用到了三相逆变器,输入的三相电流必然要经过多次换向,结果是让定子电流在换向区出现较大失真,这就导致了输出转矩出现波动现象[11-12]。也可以通过实验来验证这个说法,将结果用图5 的对比图来说明。图中可以看出,电压的每次换向都会引起电磁转矩的一次波动。
3.2 转矩波动控制方法
(1)脉冲发生器中误差宽度的影响
从矢量控制方程入手[13],分析影响转矩的因素:
结合式(4)和式(6)两个方程,可得:

在模型中,采用电流跟踪型PWM 技术作为逆变器的通断控制方式,由电流滞环跟踪器来控制逆变器,如图6 所示。
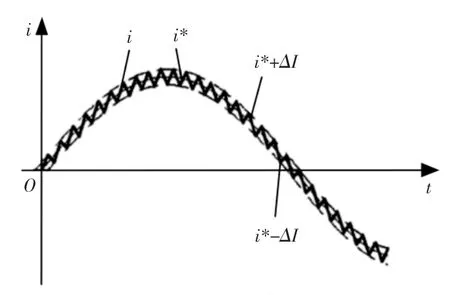
图6 电流误差Fig.6 Current Error


图7 不同滞环宽度分析结果Fig.7 Hysteresis Width Analysis Results
图7 经过比较可知,通过减小滞环宽度可有效控制输出转矩波动。
(2)转子磁链给定值的影响
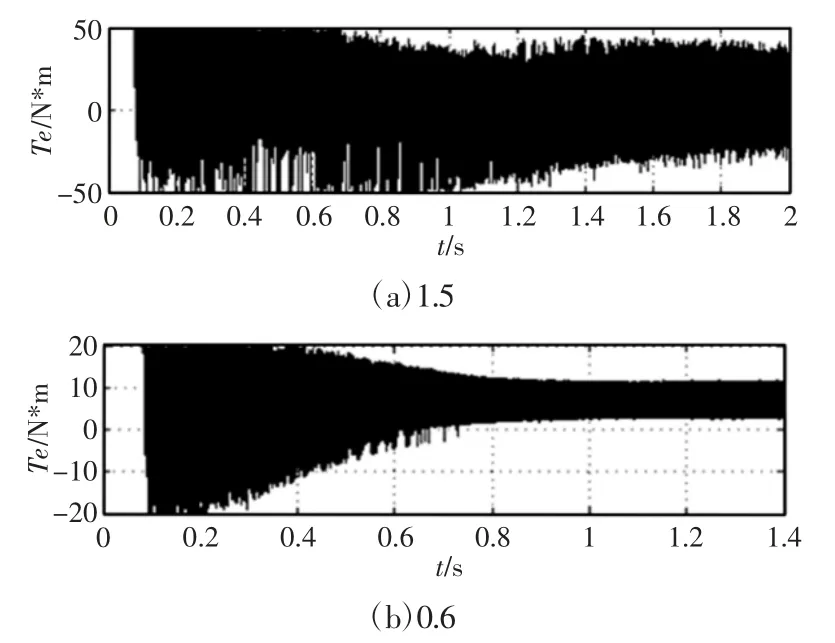
图8 不同磁链给定值Fig.8 Different Flux Given Value
由式(11)可知,Te直接受到磁链值影响,同理也对电磁转矩的波动有较大的影响。不同取值对比结果,如图8 所示。
从图中可以很明显看出,在磁链为1.5 时,转矩上下波动达到100Nm,而将磁链给定值设为0.6 时,转矩波动降到不足30。
4 基于Pharlap 系统实时分析
基于Simulink,根据动力传递系统建模原理与方程可搭建如图9(a)模型,为了研究方便,将其封装成独立的左右驱动轮加简单从动轮的模型。从动轮可视为纯滚动而不需要考虑滑转率,但需要考虑它的滚动阻力以及分担的车辆对地面的正压力。所以在模型中从动轮模块反映为它的滚动阻力模块。另外仿真结果不采集从动轮的数据只分析主动轮运行情况,模型,如图9(b)所示。为了提高效率以及进一步验证电机控制模型及波动控制措施的有效性,基于NIPXI 硬件平台,在Pharlap 系统下对模型进行实时仿真。这里所用NIPXIe-1082,如图10 所示。首先对Simulink 模型的输入输出接口进行封装,然后配置目标文件,选择NIVeristand.tlc 文件作为目标编译文件。编译完成后生成的dll 文件将会保存在同一个目录下。在系统定义文件中,定义实时目标机为Pharlap 系统并设定IP 地址,该地址要与PXI 相同。加载上一步编译好的dll 模型文件,并设置好控制参数。

图9 系统Simulink 模型Fig.9 System Simulink Model

图10 PXI 系统组成图Fig.10 PXI System Component
在Workspace 中定制仿真所需要的控件并与模型适配。如:输入控件用来表示驾驶员输入量;波形显示控件用来显示滑转率、附着系数等等。运行刚刚建立的项目,VeristandEngine 会自动将模型部署到PXI 实时目标机中进行实时仿真。
选取低附着路面、对开路面、对接路面等三种工况进行分析:第一种工况,车辆行驶于结冰路面,驾驶员的输入转矩为1000Nm,结果,如图11(a)所示;第二种工况,模型在对开路面上运行,左边路面是高附着路面,右边为低附着路面,驾驶员输入转矩为1000Nm,如图11(b)所示;第三种工况,在高附着路面启动,0.5s 后进入低附着路面,驾驶员的给定转矩为1000Nm,实时结果,如图11(c)所示。
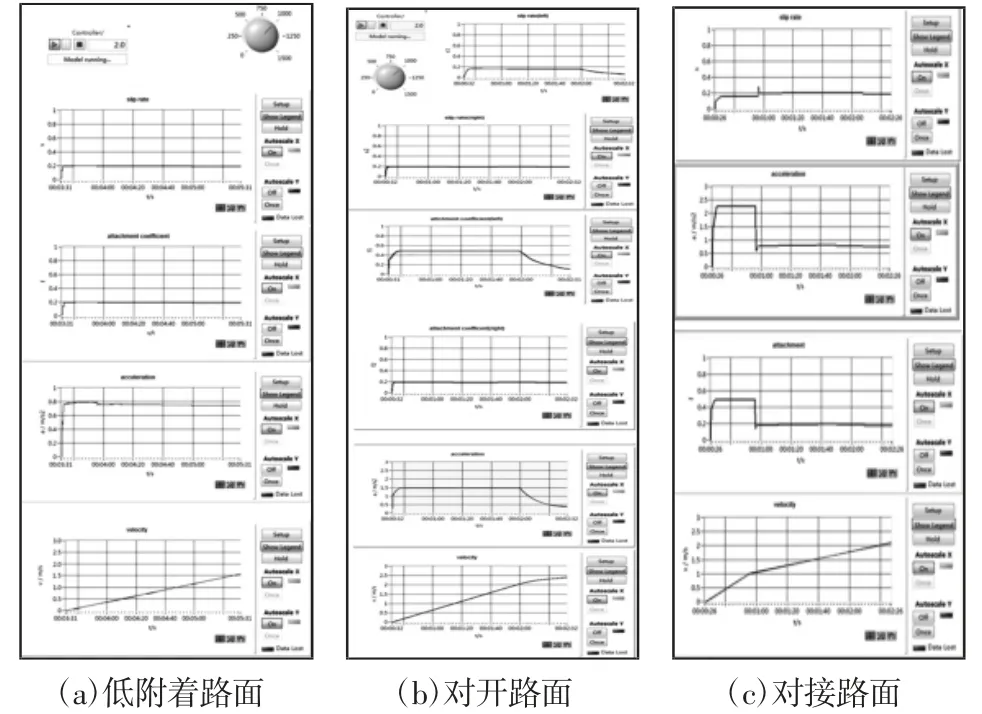
图11 三种路况分析结果Fig.11 Three Kinds of Traffic Analysis Results
图11(a)可知,一个控制模块,用于控制模型的启动与停止;一个输入模块,可以实时的调整驾驶员输入转矩,这里设置为1000Nm。下边显示控件分别表示滑转率、附着系数、车身加速度、车身速度的曲线、输出转矩等。车轮的滑转率控制在0.2 附近,车辆在此工况下的附着系数控制在0.2,车辆的速度和加速度均未出现明显的波动或剧烈变化。对于滑转率的控制效果很好,并且大大缩短了仿真时间提高了效率。图11(b)可知,在此工况下,车轮的滑移率在较短的时间内即可达到最佳状态,达到0.2,车辆运行平稳,附着系数达到0.2,达到此工况的最大值,车辆运行平稳。图11(c)可知,路面发生变化前滑移率低于0.2,附着系数达到0.5,此时车辆的加速度较大,当进入低附着系数路面时,滑移率达到最佳值,而附着系数将至0.2,此时加速度迅速降低。分析结果可以看出,响应迅速,在路面变换的时刻,控制器能够在地面附着系数突然降低时立即动作,迅速减小输出转矩,让车轮不会发生剧烈打滑,整个仿真过程与真实时钟接近,实时仿真效果良好。在模型运行过程中,为了保护逆变器,脉冲发生器中误差宽度取10;在电机启动阶段取磁链给定值为0.96,当电机稳定运行后让它降至0.6,通过调整以上参数可知,转矩波动幅度从100 降至25 左右,降低了转矩波动。
5 结论
基于电传动车辆轮边电机控制模型,对输出转矩波动原因及控制方法进行分析,基于Pharlap 系统利用NI PXI 做目标机,对选择不同工况对转矩波动控制方法进行实时仿真,结果可知:(1)转矩给定不稳定、电流和转速等反馈信号的检测误差较大、电流换向等是影响转矩波动的重要原因;(2)通过调整脉冲发生器中误差宽度、转子磁链给定值等可有效控制波动幅度,波动幅度得到明显降低;(3)基于Pharlap 系统和NI PXI 硬件平台不同工况实时仿真表明了分析结果的可靠性,为此类设计控制提供参考。

