基于一阶波动方程的正演研究
沈天晶,胡叶正
(西南石油大学 地球科学与技术学院,四川成都 610500)
地震正演是在已知地下岩层空间结构与介质参数的情况下,通过数值模拟来模拟地震波的传播。模拟结果中包括了走时信息与波场信息,反映了地下结构的空间规律与介质信息。正演数值模拟不仅是地球物理的基础,也是其重要组成部分。通过对正演模拟的研究发现,一阶的声波波动方程的有限差分模拟是最常用的方法[1-2]。尽管许多学者对其求解方法与模型离散进行了优化,但也增加了计算量,降低了计算效率。考虑到上述问题,本文利用一阶声波波动方程进行正演模拟,同时利用交错网格对其进行求解,利用CPML进行边界处理。在计算效率的提升方面,本文利用了OpenMP与mpi对程序进行并行化。
1 CPML吸收边界
利用交错网格对一阶声波波动方程进行求解,将质点震动速度,波场应力与模型属性定义在网格上。其中比较非常关键的一点就是选取了CPML吸收边界,原理如下:
二阶CPML吸收边界的吸收因子为:

在时域中,在拉伸坐标中的偏导数的求取公式如下:

上述公式的卷积运算可以利用递归卷积法进行运算,公式如下:

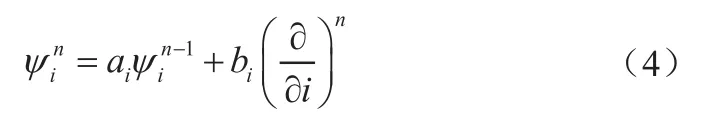
式中,n为时间步长,ai与bi为系数,由下式给出:

由上述公式,二维二阶声波方程在拉伸坐标下的公式为:

由公式(3)可知:

将公式(7)与公式(3)带入公式(6),可得:

公式(7)即为二阶声波方程的CPML吸收边界公式。
一阶的CPML吸收边界的拉伸因子为:

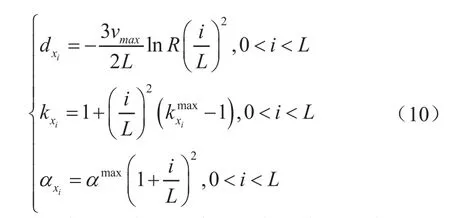
i为计算点到吸收边界内的距离,L为吸收层厚度,vmax为最大声波速度,αmax是与地震波主频有关的系数。
进一步推导可得出:

上式即为一阶声波方程CPML吸收边界的公式。
2 模型实验
通过Marmousi模型实验来验证以上方法,利用该模型的一块区域,其中包括了断层与细层,模型较为复杂。首先,利用二阶的声波方程进行正演模拟,震源主频为30Hz,空间采样为5m,时间采样为0.000 5s,CPML吸收边界厚度为16,差分精度为8,得到结果如图1(a)所示,因为模型较为复杂,反射波杂乱,分辨率较低,箭头位置甚至有频散的出现。然后在所有参数不变的情况下,利用一阶的声波方程,利用交错网格对其求解实现正演模拟,图1(b)为质点震动速度的x方向的分量。图1(c)为质点震动速度y方向的分量。这两种结果模拟了野外实际采集数据的方式,沿着水平与竖直的方向分开采集。图1(d)代表了合成的炮记录,主要反映了纵波的传播方式。可以看到相比二阶的常网格方程的结果,这种方法的精度更高,不容易频散,更能够模拟野外实际情况的采集。同时,使用了交错网格,不仅没有使计算量增加,还让结果更加精确。

图1 正演模拟结果
3 结论
利用交错网格与一阶波动方程进行数值模拟,并且利用Marmousi模型进行了模型实验。同时对二阶波动方程与一阶波动方程的模拟效果的比较可以看到,一阶波动方程模拟效果更好,精度更高,更加契合实际的采集数据。同时,一阶的波动方程更稳定,不容易频散。利用交错网格,在不提高计算量的情况下,使模拟更加精确。

