黑洞信息佯谬：落入黑洞的信息丢失了吗？＊

余明辉，葛先辉

上海大学 理学院物理系，上海 200444

1 黑洞信息的疑难

黑洞无毛定理[1]是指所有掉入黑洞的物质其所有信息都将失去，从而无法得知黑洞内部状态。外部观测者只能知道黑洞的总质量、总电荷和总角动量。虽然外部观测者无法得知黑洞的内部信息，但这些信息并未消失，只是被“封锁”在黑洞内部“看不见”而已。然而，霍金辐射[2]理论可推导出黑洞会通过热辐射蒸发。由于纯粹热辐射带不走任何的信息，但在黑洞辐射的最后，所有的内部信息将彻底消失——黑洞信息佯谬。显然，这一结果不仅会破坏物理学中许多重要定律，如重子数守恒、轻子数守恒等，而且会给目前以量子力学的基本原理——幺正性与几率守恒为基础所取得的所有重要成果带来灾难。因此，黑洞信息丢失问题这一物理学危机，成为广义相对论与量子引力这两大物理理论碰撞的焦点。

1997年，霍金(Stephen Hawking)和另一位相对论专家索恩(Kip Thorne)就曾与粒子物理学家普瑞斯基(John Preskill)打赌(图1)：霍金与索恩认为黑洞发出的辐射过于杂乱无章，以至于即使理论上也无法检测到任何关于黑洞的有用信息；普瑞斯基的观点则是，即便物理学家可能需要一套完整的量子引力理论来完美解释其背后的机制，但信息仍会以某种方式逃离黑洞。

图1 从左至右依次为普瑞斯基、索恩和霍金(图来自百度网站)

2004年7月，霍金突然宣布他输了，理由是：根据黑洞互补理论[3]，对于黑洞内外两个观测者分别而言，穿过黑洞事件视界的信息既反射出来又进入内部，永不逃逸(因为没有人可以同时观察到两种情况，所以并不会产生矛盾)。霍金愿赌服输，以一本百科全书作为赌注赠给了普瑞斯基，但索恩却拒绝认输，为故事后来的发展埋下伏笔。在近期的研究中，这个问题终于迎来突破性进展。理论物理学家发现，黑洞内部的信息的确从黑洞中完全逃逸出来，并没有任何信息的丢失。为表彰对这一系列研究作出重要贡献的几位杰出物理学家，2021年的新视野物理学奖颁发给了阿姆黑利(Ahmed Almheiri)、马克斯菲尔德(Henry Maxfield)、恩格哈尔特(Netta Engelhardt)和彭宁顿(Geoff Penington)，以表彰他们对黑洞及其辐射量子信息内容计算所作出的贡献。虽然对于解决方法的细节还存在诸多争议，但相信这个问题即将迎来终结。本文将以黑洞信息佯谬的提出为起点，以时间顺序来介绍此工作的历史背景与相关进展。

2 黑洞的历史

爱因斯坦于1905年创建了狭义相对论，1915年又在狭义相对论的基础上创建了广义相对论。广义相对论是物质世界的时空理论和在时空中物质运动的普遍理论。基于爱因斯坦伟大且富有哲学的思想，其将万有引力解释为时空的弯曲，认为万有引力区别于其他力是一种几何效应。广义相对论的核心是爱因斯坦场方程：

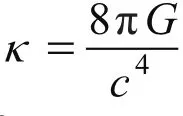
场方程的第一个精确解是史瓦西(Schwarzschild)1916年给出的静态球对称真空解[4]。它描述了真空中球对称黑洞的情况，此后将该解称为史瓦西黑洞解。得到的时空线元为：

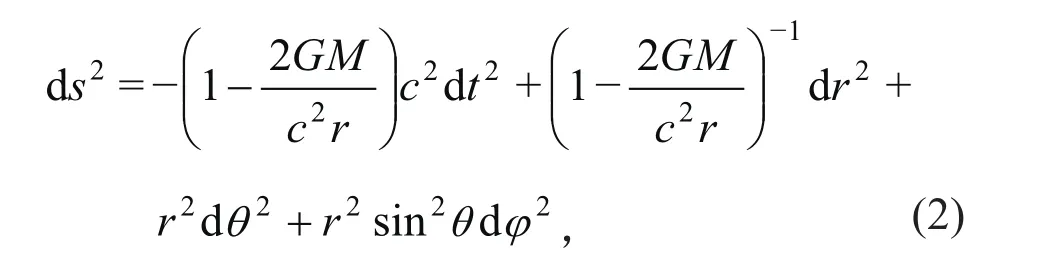
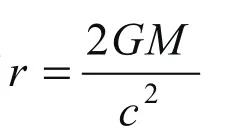
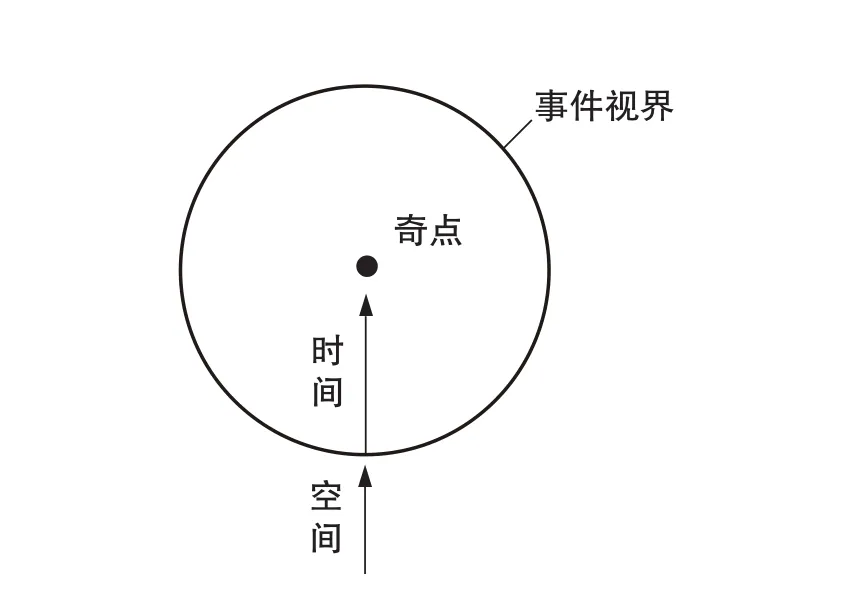
图2 黑洞事件视界和奇点简图(图来自Google 网站)

3 霍金辐射的发现

黑洞热力学的发现使20世纪70年代成为黑洞研究的黄金期。类比热力学的四大定律，黑洞也存在与之对应的四大定律，称为黑洞力学四大定律。热力学定律中最特殊的属热力学第二定律[9]，因为它是热力学中唯一标明了时间箭头的物理定律，即一个孤立系统的熵永不随时间而减少。黑洞力学第二定律由霍金于1971年在宇宙监督假设[10]和强能量条件成立前提下证明得出：黑洞的事件视界面积在顺时方向永不减少。这一定律也被称为黑洞面积定律[11]。我们不妨类比联想，黑洞似乎是具有温度和熵的存在，这一猜想最先是贝肯斯坦(Jacob Bekenstein)在1972年提出的[12]。他认为黑洞有熵且正比于黑洞事件视界面积。这一猜想却一直遭到相关同行强烈的反对，因为若黑洞真的是一个热力学系统具有温度与熵，那么它应该具有热辐射，但在当时黑洞被认为是一个“只进不出”的物体，任何物质掉入黑洞将无法逃逸出来，不可能会有热辐射。

1973年，霍金对黑洞的研究有了突破进展，他在弯曲时空中引入量子场论，严格证明了黑洞存在热辐射[2]，黑洞确实具有温度，黑洞表面积就是黑洞的熵。区别于经典物理中的真空就是空无一物的状态，量子物理中的真空到处都存在着量子涨落，不断产生具有正负能量的正反虚粒子对，随后很快就湮灭恢复为真空状态。根据量子力学不确定性原理可以计算出虚粒子对产生和湮灭的时间极为短暂。虚粒子对不断地产生与湮灭，一个粒子和它的反粒子会分开一短暂的时间。由于黑洞事件视界附近的引力场非常强，于是有四种可能：①正反粒子均落入黑洞内部；②正反粒子在黑洞外部重新相遇并湮灭为光子；③正能量粒子落入黑洞内部，负能量粒子飞向远方出现在黑洞外部；④负能量粒子落入黑洞内部，正能量粒子出现在黑洞外部(图3)。①②与黑洞热辐射产生无关，正是③④导致黑洞热辐射的产生。霍金计算了各种情况出现的概率，发现④最为常见。由此推论，黑洞有选择地俘获负能量粒子，导致一种不对称、可观测效应产生，即黑洞自发损失能量，也就是损失了质量。这一现象对于无穷远观测者来看，黑洞辐射出粒子，即黑洞在蒸发。

图3 黑洞附近的真空涨落(图来自Google 网站)

1976年，霍金在文章中仔细讨论了黑洞蒸发所引起的问题[13]。黑洞的量子理论导致一种新的不可预测性。根据量子力学基本原理，假设黑洞形成之初是纯量子态的，由于黑洞辐射是完全的黑体辐射，除了温度没有其他任何信息。在黑洞蒸发殆尽后，描述系统状态的信息在黑洞中丢失，因此最终态不是纯态而是一个混合态。这一关于黑洞信息是否丢失的问题就是著名的“黑洞信息佯谬”[14]。

该文章发表后，许多物理学家对此问题表现出极大的分歧并提出各自的解决方法，主流观点有三种：①信息丢失，同霍金观点一致，黑洞全部转化为热辐射，组成黑洞的所有信息随着黑洞蒸发永远地消失了；②信息守恒，在黑洞的霍金辐射过程中，黑洞初态的信息被释放出来并在末态回到纯态，整个物理过程中信息是守恒的，这与当时研究量子引力的物理学家包括从事粒子物理进入这一领域的物理学家的观点一致；③信息残留，落入黑洞的信息一部分被霍金辐射带出，另一部分可能在黑洞蒸发的最后作为“残留物”保留下来，或者说黑洞蒸发到一定程度就不再继续蒸发，存在某种机制限制这一过程。总之，对于这一问题的相关研究仍在继续进行。

4 关键的佩奇曲线

在霍金提出黑洞信息问题之后的20多年中，物理学家一直找不到问题的解决方案。与这些物理学家一样，霍金曾经的研究生佩奇(Don Page)也在考虑这个问题，但他与导师当时的想法完全相反。佩奇认为信息是能够从黑洞的蒸发中释放出来的，但这一过程如何实现呢？他认为物理学家忽略了一个重要效应——量子纠缠。虽然霍金辐射本身是不携带任何信息的，但一旦考虑整个系统，即辐射出的粒子与掉入黑洞内的粒子相互纠缠，就如同用密码加密数据一样，辐射出的粒子可以携带信息从黑洞中逃逸出来。

1993年，佩奇预测了黑洞与辐射之间的总纠缠量，即纠缠熵，并画出“佩奇曲线”[15]。该曲线呈一个倒“V”形，表明在黑洞蒸发开始阶段，由于还未发射任何辐射，纠缠熵为零。蒸发初期，随着辐射纠缠熵开始逐渐增加，这符合霍金的预计。然而若黑洞辐射最后保留了信息，那么纠缠熵会再次变为零，因为此时不存在黑洞。整个过程一定存在某一个时刻，经过该时刻之后纠缠熵逐渐下降至零，称该时刻为“佩奇时间”(图4)。佩奇为黑洞信息问题的解决开辟了道路，他确信如果信息能够从黑洞中释放，那么通过计算会发现纠缠熵遵循佩奇曲线。

图4 佩奇曲线(蓝线为黑洞热力学的熵；红线为霍金计算的熵；黑线为佩奇得出的熵。图来自quantamagazine网站)

问题变得更严重了！物理学家一直认为，只有在微观尺度下量子引力理论才起作用，但从佩奇的观点来看，处于佩奇时间的黑洞虽然蒸发了一部分，却依然与量子尺度相差巨大。佩奇的分析使得信息问题变成一个悖论，它暴露了半经典近似中的一个矛盾。

从某种方面来看，佩奇为物理学家指明了方向——只要计算纠缠熵并绘制出纠缠熵随时间演化的曲线。若曲线遵循佩奇曲线，则说明信息守恒粒子物理学家获得胜利；否则说明信息将会丢失，相对论主义者将会在教会中分享胜利果实。

5 巧妙而强大的工具

1994年，美国理论物理学家、弦理论的创始人之一苏士侃(Leonard Susskind)，基于贝肯斯塔关于熵的深刻见解(第2节提到黑洞熵正比于事件视界面积)结合其他物理学家的想法，提出全息原理[16]。他猜测量子力学与引力的结合要求：在一个d维空间中，如全息投影一样，可以将所有量子态信息等价编写于一个（d-1）维的全息面上。如此大胆的想法给予物理学无限可能。让我们来联想一下黑洞：如果黑洞是一个量子态，那么根据全息原理它可以将所有的信息都投影在低一个维度的面上，即黑洞表面，亦事件视界。那么物理学家只需要研究事件视界面上的信息就能得知黑洞的信息。当然，这仅仅是一个猜想。

时间来到1997年，年仅29岁的物理学家马达尔西纳(Juan Maldacena)带着他的AdS/CFT对偶[17]叩响了量子引力的大门。他发现在一种特定情况下，种种证据表明：一个存在引力的五维时空完全等价于其边界上无引力的四维时空。经过深入研究之后，他又进一步推广为：一个(d+1)维AdS时空的量子引力理论和一个定义在这个AdS时空边界的共性场论对偶，即AdSd+1/CFTd对偶。左边的AdS代表一个曲率为负的时空，即反德西特时空(anti-de Sitter)，右边的CFT代表等价的时空的共形场理论(conformal field theory)，也就是具有共形对称性的量子场论；右下角字母分别代表时空相应维度(图5)。

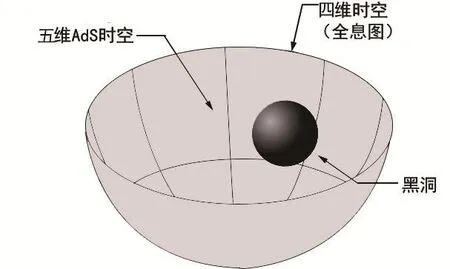
图5 AdS/CFT示意图(图来自Google 网站)

AdS/CFT对偶与全息原理结合得天衣无缝，对偶意味着完全等价，即一个物理系统可以有两种完全等价的描述方法，虽然两种描述方法看起来好像很不一样。当我们在一种方法研究上举步维艰时，完全可以在另一种方法研究上游刃有余！因此，它成为物理学家用于高能物理、量子引力、凝聚态、核物理等方面的一种全新工具。

6 简单却神奇的方法

将对偶的两个方面联系起来的关键是物理学家提出的量子极值表面。2006年，日本物理学家笠真生(Shinsei Ryu)和高柳匡(Tadashi Takayanagi)给出全息纠缠熵假设[18-19]。根据AdS/CFT对偶的观点，对于一个对偶于AdS时空的边界A中的量子场论，理论上可以通过引力计算得到A边界面与其子区域B之间的纠缠熵。他们猜想边界量子场论中的AB两区域之间量子纠缠熵等价于高一维的AdS时空中极小曲面的面积(图6)，表达式为：

其中A代表AdS时空中一个面的面积，G是引力常数，min表示所有以B区域为边界面中最小面积的面。这个特殊的面称为极小面，公式(3)也被称为RT公式。

这个神奇的猜想不仅能够作为一个漂亮、简单的方法计算具有很强耦合的场论的纠缠熵，而且能够有更多的预言。经过简单的分析发现，由于G值非常小(10-11数量级)，得出的量子纠缠熵是一个非常大的量。从之后的许多检验结果发现，RT公式只是给出零级近似的情况而忽略了一阶之后的修正。若遵从完整的量子力学理论，RT公式只是基于时空几何的一个经典理论，未考虑量子理论带来的修正。这又激发起了后续的广泛研究。

2015年，恩格哈尔特(Netta Engelhardt)等人[20]考虑量子修正以及经过量子修正后的纠缠熵(称之为广义熵)对极小面影响的两个因素，得出了广义熵半经典表达式：

此时的面积不再是极小值的面积，而是广义熵取极小值的面的面积，这个特殊面称为“量子极值面”。式(4)右边第一项仍然代表面积；第二项是量子效应引起的修正，代表极值面包围区域内所有量子场所产生的冯·诺依曼熵；ext表示寻找所有的极值面且{∑}这些面的广义熵均达到极值；min表示在所有极值面{∑}中，广义熵极小的那个面。

图6RT纠缠熵示意图，边界上阴影区域B的纠缠熵等价于高一维AdS时空中以B为边界的极小曲面面积(图来自Google 网站)

至此，有了工具和方法，物理学家已经严阵以待，准备对如何计算黑洞蒸发过程的纠缠熵问题发起攻击。

7 蒸发黑洞的模型

这项工作开始于2018年10月，当时高级研究所的阿姆黑利(Ahmed Almheiri)正在想如何制定黑洞蒸发的装置。他考虑一个在AdS时空中蒸发的黑洞，因为对偶这个过程可以完全等价地在边界CFT中描述，而CFT是基于量子力学的，根据量子力学原理的幺正性，自然得出结果：边界的确保留了信息，黑洞也必须如此。到目前为止，至少可以实现在AdS时空中检测一个蒸发的黑洞的熵是否遵循佩奇曲线，但是问题没这么简单。虽然理论是正确的，但实际的实验环境与我们现实生活的时空或渐进平直的时空不同。在AdS时空中黑洞实际上不会蒸发，因为这个时空的边界犹如一道无形的屏障，辐射像高压锅中的蒸汽一样充满狭小的整个空间，无论黑洞发射什么，最终都将被吸收回来，系统最终达到一个稳态(图7)。

图7 两种时空对比：左图为渐进平直时空，无边界；右图为AdS时空俯视图，曲率为负，存在边界(图来自quantamagazine网站)

因此，AdS时空中的黑洞经过足够长的时间会趋于稳定，形成一个稳态，且达到热平衡，维持着不变的温度。解决这一问题的方法也很简单，阿姆黑利接受了同事的建议，在边界上放置一个等效的蒸汽阀用以排除辐射并防止辐射回落[21]。问题解决后，启动装置，黑洞开始辐射，研究人员同时观察空间发生了什么。

他们发现在黑洞蒸发的初期，边界的纠缠熵上升，由于黑洞是整个空间中唯一的物体，故推测出其纠缠熵也在上升。到目前为止结果还是与霍金原始计算符合得不错。随后某一时间，量子极值面突然出现在黑洞事件视界内，它成为熵变化的主导因素，熵开始下降！这也是所有计算中首次出现的[22]。

纠缠熵随时间演化的曲线确实遵循佩奇曲线。现在研究人员能够确认黑洞释放了信息，它以量子纠缠成为可能的高度加密形式输出。

8 孤岛的浮现

2019年8月，阿姆黑利和同事将注意力转向了剩余的最后一个问题——怎样计算黑洞辐射的纠缠熵[23]。

研究人员通过量子极值面的方法可以算出一个正在蒸发的黑洞的广义熵，它来自于黑洞事件视界外的量子场，而考虑霍金辐射的时候，辐射熵是来自于内部。在蒸发过一段时间后，量子极值面突然出现，黑洞内部被划成了两处区域，一处是具有辐射的区域1，另一处位于黑洞内部的区域2，处于区域2中的粒子被量子极值面隔离，它们不再属于黑洞的一部分，因此也不再对纠缠熵有贡献。区域2与辐射区域完全隔离，犹如茫茫大海中的一座孤岛，因此称区域2为“岛”(图8)[24]。

图8 量子极值面的出现使得黑洞内部被划分成了两个区域，而且具有辐射的区域1与内部区域2隔离，区域2称为“岛”(图来自quantamagazine网站)

“岛”的效应导致霍金辐射的纠缠熵降低。仿照量子极值面方法中给出的广义熵公式，更进一步，研究人员给出了辐射熵表达式[25]：

类似于式(4)，等式右边第一项代表面积，第二项代表量子场所产生的冯·诺依曼熵。值得注意的是，量子修正中不仅仅考虑了辐射所带来的影响(辐射用字母R表示)，还考虑了“岛”的贡献(用字母I表示)，岛的边界(用∂I表示)就是量子极值面，出现在第一项中[26-29]。利用新的公式，研究人员计算得出黑洞发出的辐射熵也同样遵循佩奇曲线。综上，黑洞蒸发的全过程以及其纠缠熵随时间的变化可用图9描述。

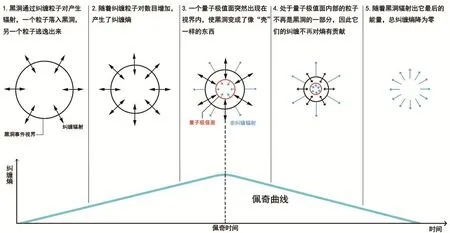
图9 黑洞蒸发过程中纠缠熵随时间演化的曲线完全遵循佩奇曲线(图来自quantamagazine网站)

9 佯谬的结论与展望

经过一系列的工作，黑洞信息佯谬可能不再称为佯谬，物理学家终于完成了对佩奇曲线的重现！标志着困扰了物理学界近50年的问题迎来终结：在黑洞蒸发的过程中，确实释放了信息，没有任何的信息丢失。量子引力理论又迈前了一步！但同时又伴随着更多问题的产生：一方面，为什么量子极值面会突然出现且为何使得内部粒子不再属于黑洞？关于“岛”出现的解释目前研究还在继续[30-35]；另一方面，上面的所有理论都还只是半经典的理论，我们仍然对辐射粒子的量子态一无所知。最重要的是，计算结果仅仅表明信息逃逸出了黑洞，并没有说明信息是如何逃逸的[36-37]。种种谜团或许只有在真正建立起量子引力理论时才可揭晓。当量子引力的大门完全被物理学家推开时，世界又会是一番怎样的景色呢？