基于PEIV模型的矿区坐标框架转换参数估计方法研究

靳文举，徐强国，吕建河，韩先楠，丁 锐

(1.兖煤菏泽能化有限公司，赵楼煤矿，山东 菏泽 274705；2.中国矿业大学，江苏省资源环境信息工程重点实验室，江苏 徐州 221116)

0 引 言

为了适应现代对地观测技术发展，特别是国家坐标系统统一要求，建立高精度矿区坐标系统框架愈发重要。矿区坐标转换参数通常采用最小二乘估计(Least Square，LS)方法[1]。近年来变量误差(Errors-in-Variables，EIV)模型其严密解法总体最小二乘(Total Least Square，TLS)日益引起学者们关注[2-4]，刘亚彬等[5]研究了总体最小二乘抗差估计在GNSS高程拟合中的应用；Xu P等[6]给出了EIV模型的概括模型方法，显著提高了TLS法的求解效率。王乐洋等[7]分析了PEIV模型方差分量估计精度问题。由于TLS法同时顾及了误差方程系数矩阵和观测向量误差，为构建高精度矿区坐标框架基准提供了重要科学基础，同时为矿区企业安全生产提供高精度测量服务成为可能。譬如矿区高程异常拟合TLS解算法，矿区坐标转换法方程病态问题[8-10]。关于PEIV模型应用于矿区坐标框架基准转换的研究较少，且未充分考虑原有和目标坐标框架观测值精度不等的情况，随机模型准确性对参数估计会有影响。本文在分析PEIV模型和方差分量估计方法的基础上，将其引入矿区坐标框架转换，研究观测值数量和随机模型对求解矿区坐标框架转换参数精度和计算效率的影响。

1 PEIV模型及其解法

PEIV的函数模型和随机模型[6]表示为：

(1)

(2)

由于系数矩阵中的元素是关于变量的函数，文献[7]将PEIV模型视为非线性函数，将其线性化为经典Gauss-Markov模型：

(3)

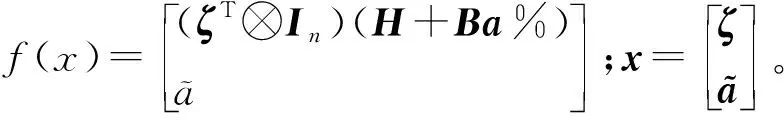
(4)

(5)

采用间接平差可表示为：

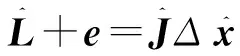
(6)

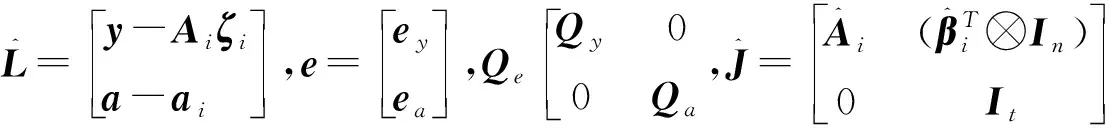
(7)

通过迭代计算，参数估值为：

(8)

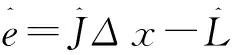
(9)

2 最小范数二次无偏估计法(MINQUE法)

最小范数二次无偏估计法是一种通过满足最小范数条件得到单位权方差分量估值，是一种更为准确的随机模型验后估计方法。王乐洋等[7]给出了经线性化的PEIV模型最小范数二次无偏估计：

(10)

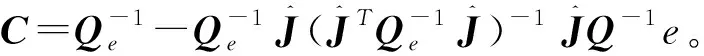
(11)

本文将结合PEIV模型的方差分量估计方法定义为PEIV-VC模型。

3 矿区坐标框架基准转换PEIV模型方法

为了构建高精度矿区坐标基准，将PEIV模型和PEIV-VC模型应用于矿区平面坐标转换实验研究。四参数坐标转换模型可表示为：

(12)

3.1 初始-目标坐标框架观测误差相同

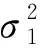
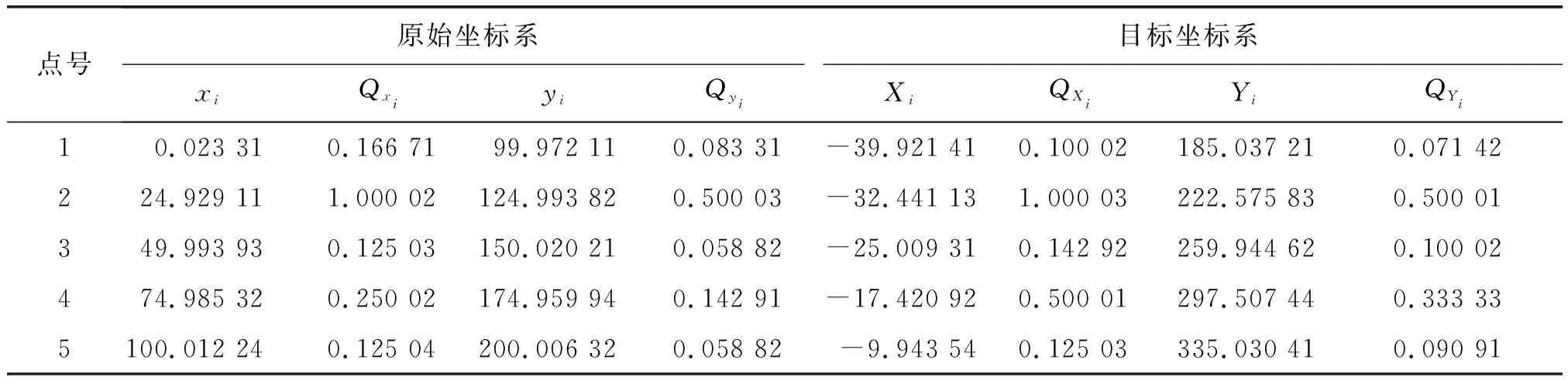
表1 坐标点数为5时四参数坐标转换模型协因数及坐标观测值/m

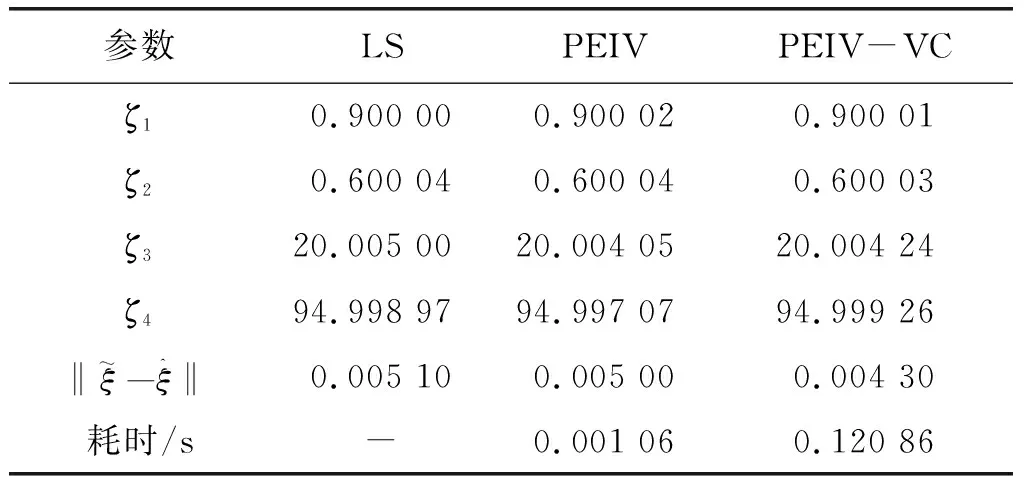
表2 初始和目标坐标框架观测值误差相同情况下计算结果(坐标点5)

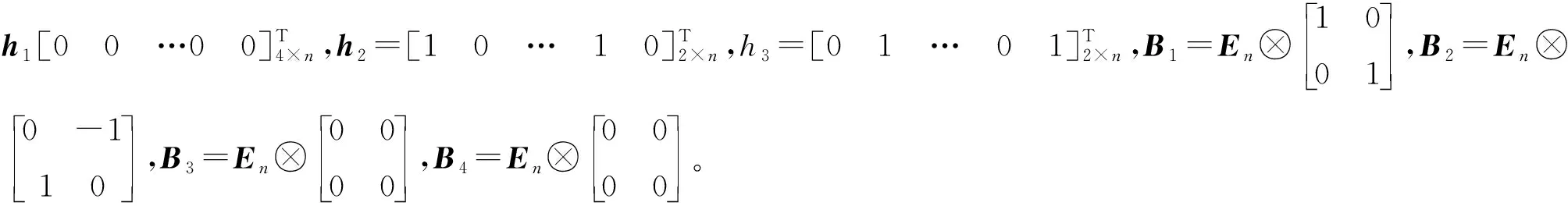
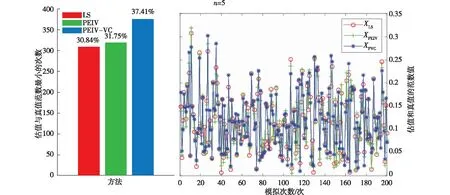
图1 观测值误差相同时统计结果(坐标点5)

坐标点个数为15时，3种方法参数估值及其精度信息与计算效率见表3，模拟实验统计结果如图2所示。

坐标点数为25时，3种方法求参数估值及其精度信息与计算效率见表4，模拟实验统计结果如图3所示。

对比表2、表3和表4，当初始和目标坐标系观测值误差相同时，3种方法都能有效求得坐标转换参数，PEIV-VC模型参数估值最优，PEIV模型参数估值次之，LS法参数估值精度最低。随着坐标观测值数量增加，3种方法参数估值精度逐渐提高，且PEIV模型参数估值逐渐接近PEIV-VC模型结果，但PEIV模型求解所需时间仅为PEIV-VC模型所需时间的3.61%-3.76%。由1 000次模拟实验统计结果可知，当坐标观测值数量较少时，3种方法求得最接近真值的参数估值次数差别较小，随着坐标观测值数量增加，PEIV模型方法求得最优参数估值概率增大。

表3 初始和目标坐标框架观测值误差相同情况下计算结果(坐标点15)

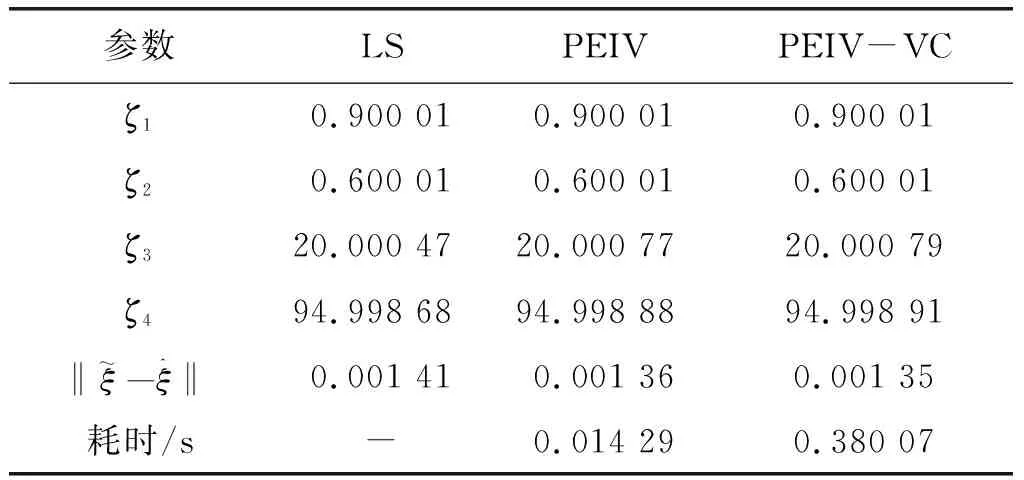
表4 初始和目标坐标框架观测值误差相同情况下计算结果(坐标点25)

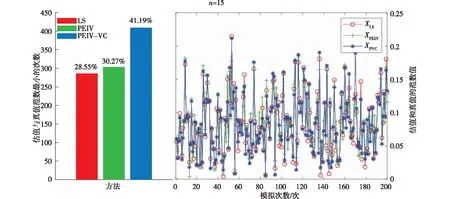
图2 观测值误差相同时统计结果(坐标数为15)

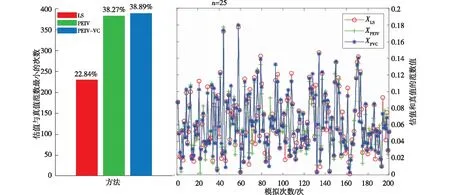
图3 观测值误差相同时统计结果(坐标数为25)

3.2 初始和目标坐标框架观测值误差不同

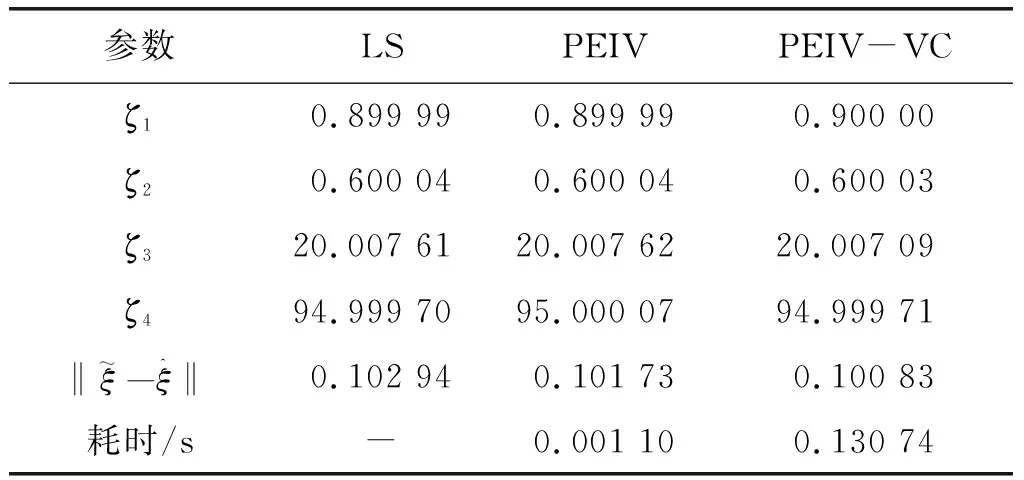
表5 初始和目标坐标框架观测值误差不同时计算结果(坐标点5)

表6 初始和目标坐标框架观测值误差不同时计算结果(坐标点15)

表7 初始和目标坐标框架观测值误差不同时计算结果(坐标点25)

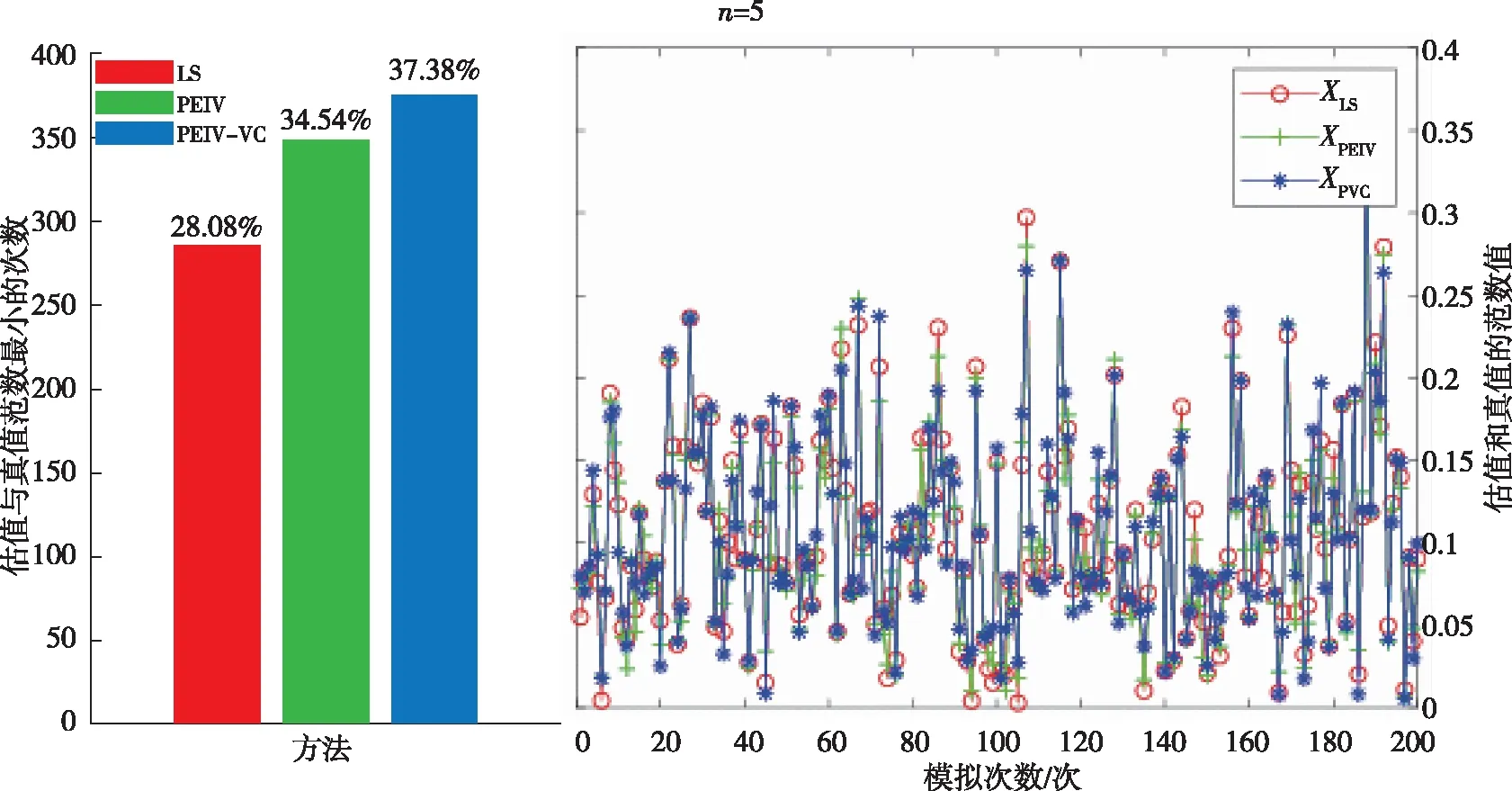
图4 观测值误差不同时统计结果(坐标数为5)

图5 观测值误差不同时统计结果(坐标数为15)

图6 观测值误差不同时统计结果(坐标数为25)

对比分析可知，当初始和目标坐标框架观测值误差不同时，3种方法仍能有效计算坐标转换参数，当坐标观测值数量增加时，PEIV-VC模型参数估值优于PEIV模型，且相较于观测值误差相同时的结果提高明显，表明考虑随机模型十分重要，但计算代价显著增加。PEIV-VC模型始终能在修正随机模型的同时更大概率地求得最优参数估值，表明将PEIV-VC模型应用于矿区平面四参数坐标框架转换的重要意义。

4 结 语

本文将PEIV模型应用于矿区坐标框架转换参数估计问题，并通过方差分量估计对随机模型进行修正。根据矿区数据特征模拟矿区测量数据，分析了坐标观测数量和随机模型对求解矿区坐标框架转换参数精度和计算效率的影响。① 验证了PEIV模型应用于矿区坐标框架转换参数估计的可行性及修正随机模型的重要性；② 坐标观测数量能够有效提高矿区平面坐标转换参数求解精度；③ 当初始和目标坐标框架观测值等精度时，PEIV模型在一定程度上可以通过增加观测值数量，在节省大量计算时间的同时达到逼近PEIV-VC模型求解精度的效果；④ 当初始和目标坐标框架观测值不等精度时，PEIV-VC模型为矿区坐标框架转换的最优选择，为研究多源和海量矿区数据处理问题提供了参考。