天广HVDC 换流阀阻尼电阻O 型圈加速老化试验及使用寿命研究

罗远峰，雷朝煜，吴保义，郝菁菁，张 松，魏孟刚

（1 中国南方电网超高压输电公司天生桥局，贵州兴义510670；2 南瑞集团中电普瑞电力工程有限公司，北京102200）

高压直流输电（High-Voltage Direct Current transmission，以下简称“HVDC”）在电网中应用日益广泛，满足了电能远距离传输需求，提高了电网运行效率。阻尼电阻是HVDC 换流阀装置核心功能器件之一，能够抑制回路振荡，限制晶闸管开通、关断时阻尼电容充放电电流幅值和变化率di/dt，保证阻尼电容和晶闸管等器件安全、可靠运行［1-2］。换流阀阻尼电阻发热量大，一般采用水冷散热方式，水冷电阻具有体积小、重量轻、功率密度大等优点［3］。O 型圈是水电阻接口密封器件，其性能优劣直接决定了水冷电阻密封性能，进而影响阻尼电阻器使用寿命。

O 型圈密封性能主要来源于其高弹性和体积不可压缩性。受压状态下O 型圈会对其工作面产生强大的弹性应力，从而使冷却液体（循环水）不致泄漏［4］。但O 型圈这种密封能力不是恒定不变的，它会由于长时间受力而产生应力松弛、在高温和介质中长期工作而产生材料老化、在低温环境下变硬发脆而失去弹性等，导致密封性能下降，无法承受高压去离子循环水，最终发生漏水事故［5］。因此，O 型圈性能直接决定了换流阀水冷电阻器使用寿命，如何在短期内评估换流阀阻尼电阻O 型圈的老化性能，预测其使用寿命，对于阻尼电阻器密封设计及工程应用产品密封性能控制具有重要意义。

本文通过研究换流阀阻尼电阻O 型圈老化机理，提出了换流阀阻尼电阻O 型圈加速老化试验方案及试验数据的处理流程，在不改变试品失效机理和不增加新失效因子前提下，提高试验温度应力，加速试品失效进程，再根据试验数据，确定寿命模型中的待定参数，进而估算出试品在实际使用工况条件下的预期寿命［6］。

1 加速老化试验方案

1.1 试品简介

天广±500kV 直流输电工程换流阀阻尼电阻为水冷式，额定电阻45Ω，额定进水流量2L/min，进水温度≤49℃。每只水电阻采用两只O 型圈用于电极接口的密封，其材质为三元乙丙橡胶（EPDM），外形尺寸及安装方式如图1 所示。

图1 天广HVDC 换流阀阻尼电阻O 型圈外形尺寸及安装方式Fig. 1 Overall dimension and installation mode of damping resistor O-ring of Tianguang HVDC converter valve

1.2 加速老化试验方案设计

换流阀阻尼电阻O 型圈在使用过程中处于受压状态，会受到机械应力、温度、湿度、介质及去离子水共同作用，从而导致橡胶老化，产生永久变形，其中温度和应力对橡胶的化学反应速度有显著影响［7］。温度和应力会破坏橡胶的分子结构，使大分子断裂，生成自由基，引发橡胶大分子氧化降解反应［8］。因此，在温度和应力作用下O 型圈老化速度决定了其使用寿命。

将样品O 型圈装配到阻尼电阻器中，并在电阻内部充满去离子水，使O 型圈机械应力、介质环境与工程现场保持一致，避免了试验条件与现场不一致带来的误差。O 型圈为橡胶材质，在正常使用条件下的老化时间长达数年，为了缩短试验时间，根据时温等效原则，在不改变失效形式的前提下，将装配好的电阻放在高温鼓风箱内，通过提高工作温度加快O 型圈老化速度，在较短时间内得到其老化特性和数据。

1.3 性能指标失效判据

O 型圈在压缩状态时，其内部会发生物理化学变化，当压缩力消失后，这些变化阻止密封圈恢复到其原始状态，于是就产生了压缩永久变形ε。压缩永久变形的大小取决于压缩状态的温度、应力和持续时间，该性能参数与橡胶材料密封性能关系最为密切［9-10］。因此，本试验失效判据指标选为压缩永久变形保留率P（1-ε）。

不同材质、不同安装方式的O 型圈失效临界值并不相同，为得到天广HVDC 换流阀阻尼电阻O 型圈的失效临界值，专门设计了水压试验。将性能参数P 不同的O型圈装在冷却水管测试系统内，按规定的参数（试验温度30℃，试验压力1.6MPa，试验时间60min）进行静水压试验。试验过程中，压缩永久变形保留率P 低于0.3的O 型圈出现密封处出现渗漏现象，因此失效判据定为0.3。

2 加速老化试验方法及步骤

2.1 试验方法

试品数量：换流阀阻尼电阻器40 只，每只电阻器安装2 只O 型圈。

老化温度：不同生胶、硫化体系的温度上限不同，EPDM 最高为130℃，同时避免温度过高引起水沸腾，选取4 个老化试验温度，分别为65、75、85、95 ℃。

老 化 时 间： 分 别 为2、5、8、11、15、19、23、28、33、40 d。

试验设备： 电热鼓风干燥箱、水压试验设备、高精度测量仪表等。

2.2 试验步骤

步骤①：测量O 型圈初始高度h0和压缩后的高度h1，所有密封圈高度差不超过0.01mm；步骤②：将O型圈安装至阻尼电阻器内，所有O 型圈具有相同压缩量，将电阻内部充满去离子水并密封；步骤③：打开4个电热鼓风干燥箱，当电热鼓风干燥箱内空气温度分别达到预期温度时，将已装配O 型圈的阻尼电阻放进干燥箱，记录开始试验时间；步骤④：每当试验进行到一个时间节点时，从4 个温度电热鼓风干燥箱中，各取出1 只试样电阻，取出EPDM 密封圈，在室温下放置24h后测量O 型圈高度h2；步骤⑤：计算压缩永久变形率ε（ε=［（ h0-h2）/(h0-h1)］×100%)及保留率1-ε，记录数据。

换流阀阻尼电阻器O 型圈加速老化试验和耐水压试验过程如图2 所示。

图2 换流阀阻尼电阻器O 型圈加速老化和耐水压试验照片Fig. 2 Photo of accelerated aging and water pressure test of O-ring of damping resistor of converter valve

3 加速老化试验结果

不同温度条件下O 型圈性能参数P（1-ε）的数据记录见表1。

将表1 数据绘制成趋势图，如图3 所示。

表1 不同温度条件下O 型圈性能P（1-ε）数据记录表Table 1 Performance P(1-ε) of O-ring with aging time under different temperature conditions

图3 不同老化温度下O 型圈性能P（1-ε）变化趋势图Fig. 3 Change trend of performance P(1-ε) of O-ring at different temperatures

从图3 可以看出，老化时间τ 一定，老化温度T 越高，O 型圈性能P 越低；老化温度T 一定，老化时间τ 越长，O 型圈性能P 越低；性能P 和老化时间τ、温度T 不是简单线性关系。

4 数据处理及寿命预测

4.1 试验数据处理

阻尼电阻O 型圈性能参数P 随时间的变化符合动力学公式，采用坐标变化方法，将图3 中的数据转换为直线，计算出不同温度下的反应速度系数G，然后根据阿伦尼乌斯方程计算出工作温度下的反应速度系数G0，即可得到工作温度下的动力学方程［7］。动力学方程形式和种类较多，式(1) 的精确性最好，因此本文用式（1）进行回归分析。

式(1)中，G 为老化速度系数；A 为反应速度常数；τ 为老化时间；α 为经验常数，一般不随温度变化，0＜α≤1。

处理试验数据可确定常数A、G 和α 数值，进而得到适用于天广HVDC 换流阀阻尼电阻O 型圈的加速寿命模型。

为了便于数值回归分析，将式(1) 左右两侧同时取 自 然 对 数：LnP=LnA-Gτα， 令y=LnP，x=τα，α=LnA，b=-G，则式(1)可用y=α+bx 来表示。

α 值按逐次逼近法则求解，α 值范围在0～1 之间，第一次设α=0.50，计算得到xi和yi数值见表2。

对于不同的老化温度条件，按最小二乘法估算系数α 和b。

表2 当α=0.50 时xi 与yi 数值Table 2 xi and yi values when α=0.50

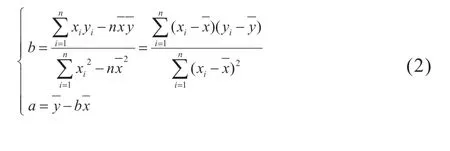
式(2)中，xi为每个老化时间长度对应的 xi=τα，τ单位为d，α 为预设值0.50，yi为每个老化时间节点对应的为xi的平均值，为yi的平均值。

计算得到，95℃温度下的a1=-0.1594，b1=-0.0956；85℃温度下的a2=-0.1603，b2=-0.0666；75℃温度下的a3=-0.1615，b3=-0.0456；65 ℃温 度 下 的a4=-0.1584，b4=-0.0308。系数a 取不同温度下回归分析值的平均值，即a=(a1+a2+a3+a4)/4=-0.1599。

将常数a 和α 代入式(1)，得到四种不同老化温度下的性能参数动力学方程。

将不同老化时间长度τ 分别代入式(3)，得到对应老化温度、不同时间节点性能参数计算值Pij，并计算式中为对应老化温度、不同时间节点性能参数实测值。

以0.01 为间隔，将α 更改为0.00～1.00 之间其他数值，得到不同的R 值，并绘制R 值变化曲线，如图4 所示。

图4 R 值随α 值变化的趋势图Fig. 4 Trend diagram of R value changing with α value

从图4 可以看出，当α=0.60 时，R 值取到最小值，因此，系数α 取0.60。

不同温度下的反应速度G 和温度T 的数值见表3。

表3 不同老化温度下的反应速度GTable 3 Reaction rate G at different aging temperatures

反应速度常数G 与温度1 /T 关系服从下式：

式（4）中：E 为表观活化能，J/ mol；R 为气体常数，J/(mol·K)；T 为热力学温度，K；B 为频率因子，d-1。

式(4) 取 自 然 对 数 得 到： LnG=LnB-E/RT ，令y=LnG，x=1/T，m=LnB，n=-E/R， 则 式(4) 可 用y=m+nx 来表示。

根据表3 数据，利用最小二乘法，计算出m=10.44和n=-4704.95，即y=10.44-4704.95x，带入式(4) 得到LnG=10.44-4704.95×1/T，如图5 所示。

图5 反应速度自然对数LnG 与热力学温度倒数1/T 的关系Fig. 5 Relationship between logarithm of reaction rate LnG and reciprocal of thermodynamic temperature 1/T

4.2 使用寿命预测

根据数据处理结果，系数 A= e-0.1599=0.8522，α=0.60，m=10.44 和n=-4704.95，分别带入式(1)、式(4)得到天广HVDC 换流阀阻尼电阻O 型圈样品性能参数P符合下式：

式(5) 中，n 为使用年限，T 为实际工作温度对应的热力学温度值。

样品O 型圈工作温度为25℃、30℃和35℃时性能P 变化趋势如图6 所示。

图6 样品阻尼电阻O 型圈不同工作温度下性能P 变化曲线Fig. 6 Performance P curve of O-ring of sample damping resistor under different working temperatures

从图6 可以看出，随着使用年限的增加，样品O 型圈的性能P 不断下降。使用温度越高，性能参数P 下降速度越快。

为了准确推测器件使用寿命，将式(5) 进行变形得到下式用于寿命预测：

从式(6) 得出工作温度与预期使用寿命关系，如图7所示。

图7 预期寿命随使用温度T 的变化趋势Fig. 7 Variation trend of life expectancy with service temperature T

经计算，工作温度为25℃、30℃和35℃时使用寿命分别为22 年、14.3 年和10 年。

本次试验样品取自天广±500kV 直流输电工程，换流阀端交流电压208.6kV，额定触发角度15°，额定直流电流1800A，额定输送容量1800MW，换流阀阻尼电阻平均水温为30℃左右，将温度值303K 带入式(6) 可得到天广±500kV 直流输电工程换流阀阻尼电阻器O 型圈预计使用寿命为5213.78d，即14.28 年。

天广±500kV 直流输电工程直流极1 于2000 年12月26 号投入运行，双极于2001 年6 月26 号投入运行。2015 年之后换流阀阻尼电阻O 型圈老化渗漏问题频繁出现，将O 型圈进行批量更换后，渗漏问题得到根本解决。样品O 型圈使用寿命与预期分析基本一致，说明了本文模型的正确性。

5 结论

本文研究了HVDC 换流阀阻尼电阻O 型圈老化机理，根据反应速率公式和橡胶材料性能参数动力学方程建立了O 型圈寿命模型，设计了加速老化试验，主要结论如下：

（1）在温度和机械应力作用下O 型圈老化速度决定了其使用寿命，应力一定情况下，工作温度越高，O型圈老化速度越快。

（2）影响O 型圈密封性能的主要性能指标P 是压缩永久变形保留率，经耐水压试验确定性能指标P 低于0.3 时，阻尼电阻在使用过程中易出现渗漏问题。

（3）通过试验数据处理和回归分析确定了寿命模型中多项待定参数，模型可用于特定工作温度下不同使用时间节点的性能分析，也可用于不同工作温度条件下的寿命预测。

（4）根据天广±500kV 直流输电工程阀阻尼电阻器O 型圈寿命模型估算其使用寿命为14.3 年左右，与现场实际情况基本一致。

本文研究的寿命模型可用于天广±500kV 直流输电工程换流阀阻尼电阻O 型圈寿命预测和状态评估，研究成果可指导现场运维，项目采用的数学模型、试验方案、试验数据处理方法可为其他工程同类研究提供参考。