翼式地下综合管廊受力性能试验与数值分析

钟世英李志康王堉众高大潮慕昕海

(1.山东建筑大学 土木工程学院，山东 济南250101；2.建筑结构加固改造与地下空间工程教育部重点实验室，山东济南250101)

0 引言

随着我国城市化进程的加快，地上空间的利用率接近饱和，提高城市主体空间的利用率与精细化对于城市发展显的愈发重要。 地下建筑包括地下车库、地下人防商场、地铁和地下综合管廊，其作用可分担地面建筑的紧密空间，优秀的规划方法也将极大地提升地上、地下的利用效率[1]，并实现绿色协调可持续发展。 城市地下综合管廊是承担城市基本管线正常运营与维修的主要围护结构，其将有利于天然气、热力、市政等的整体式有效管理，还可进一步实现综合管廊与轨道交通等的协同建设[2]，实现城市地下空间的综合利用以及资源共享。 对管廊结构体优化设计后，既可保证结构安全又可节约材料，因此管廊结构体优化设计是提高效能、促进行业精细化发展的有效手段。

针对地下管廊，众多学者做了丰富多样的研究，涉及管廊力学结构的受力原理分析、创新管廊结构的设计、抗震和抗爆等抗灾能力模拟分析等方面[3]。 胡翔等[4]和彭真等[5]设计接头和整体结构足尺模型试验，研究了管廊在受力状态下的破坏状态，作出了系统性评价；王述红等[6]和庞瑞等[7]针对装配式和现浇式的综合管廊在相同荷载情况下的变形问题进行了数值模拟，总结了装配式管廊的优点；闫钰丰等[8]、刘学增等[9]和赖浩然等[10]研究了不同土层状态下的管廊损伤演化机理；王英浩等[11]、张明书等[12]、蒋录珍等[13]和施有志等[14]分析了结构受力的合理性和特殊情况下的动力特性，初步评价了相应工况下的渗透稳定性；易建伟等[15]研究了带腋角管廊的受力稳定性，验证了外伸构造结构的受力合理性。

纵观管廊目前的形式种类，可总结其特点为“大”“重”。 现有的结构形式为混凝土围护结构，规模很大，为了保证安全，用料极多，但因此可能带来的问题是管廊本身承载性能“过剩”，以致于无法充分发挥自身承载性能至最佳使用状态。 文章在国内已有研究的基础上，依据综合管廊结构断面形式，提出了一种新型薄壁摩擦受力型综合管廊，其结构主体为通长圆柱、截面形式为环状柔性薄壁圆，材料为钢混砼结构，对其进行了室内模型试验，研究了其薄壁的受力性能，并通过建立有限元分析模型，将模拟结果与试验结果对照，验证了所提出管廊的受力优越性。

1 翼式地下综合管廊受力性能试验

1.1 试验概况

1.1.1 试验相似比

根据相似理论和模型试验物理参数确定试验模型的相似比，试验模型与原型相似需要在几何条件、受力条件和摩擦系数等方面满足一定的相似关系[16]，满足的几何、应力及外力相似系数分别由式(1)～(3)表示为

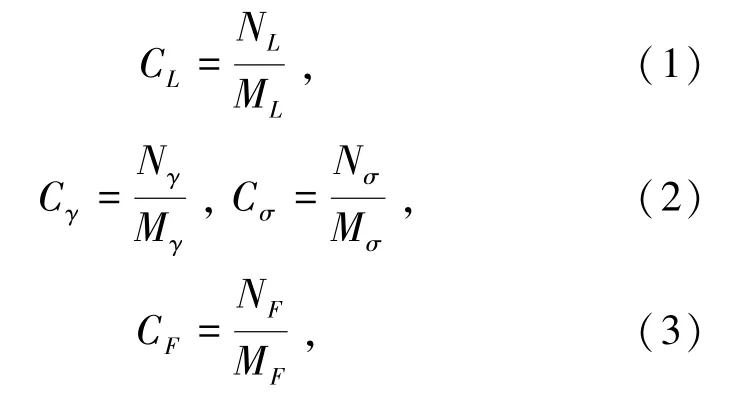
式中CL、Cγ、Cσ、CF分别为几何相似系数、容重相似系数、应力相似系数和外力相似系数，无量纲；NL、Nγ、Nσ、NF分别为原型的厚度、材料密度、材料应力和所受外力；ML、Mγ、Mσ、MF分别为模型的厚度、材料密度、材料应力和所受外力。 上述相似系数满足的条件由式(4)表示为

材料应力的相似比参数作为管廊相似比参数的主控参数，并可进一步简化为管廊材料弹性模量的相似比参数，见表1。 对比二者的弹性模量，可得应力相似比为200。 密度相似比参数作为次要参数，可参与辅助计算。 原型的密度为2.5×103kg/m3，模型试验采用的材料密度为2.4×103kg/m3，故材料密度相似系数Cγ为1.04。

表1 材料参数表

1.1.2 模型设计

模型主体是在砂土埋设下的地下管廊结构，如图1 所示，为模拟研究承载与沉降控制设计的实际情况，设计的模型结构尺寸如图2 所示，管廊主体围护采用双圆筒内接支撑的形式，外圆筒半径为11.05 cm、内圆筒直径为9.15 cm、圆筒壳体材料厚度为0.1 cm，两个圆筒之间采用异型褶皱结构连接，如图3 所示；并在上部分设3 个预应力摩擦异型锚杆，模拟实际工程中的锚杆，因此可产生一定的锚拉支护作用，使砂土与模型充分接触，提高整体侧摩阻力，锚杆长度为3 cm、外伸翼缘长度为3 cm。 管廊通长贯通布置，其长度为40 cm。 原型结构的主体尺寸是厚度为20 cm 管片拼装而成的圆环柱状管廊，试验模型采用厚度为0.1 cm 的硬卡纸；几何相似系数可根据表1，结合式(1)和(4)可得CL ＝192、NL ＝0.192。 故实际工程所采用的的拼装管片厚度约为20 cm。

图1 管廊示意图

图2 管廊尺寸图/cm

图3 管廊异型内衬结构图

1.1.3 模型箱与材料布设

研究所用的管廊主体结构布置在模型箱内，模型箱材料采用为亚克力板，通过热熔胶拼接粘合而成，在保证主体结构受力稳定的同时，最大限度地减少材料消耗和重量，节约了成本。 模型箱尺寸为60 cm×40 cm×40 cm(长×宽×高)，材料厚度为13 mm。 根据试验荷载进行加固处理:模型箱外围绑定钢板，施加围压，以便限制模型箱在加载过程中的侧向变形，减少误差，达到约束的目的，如图4 所示。 填砂时，先将模型放置在模型箱内指定位置，用自制辅助工具保证模型的稳定，并采用水平直尺校核管廊位置；定位准确后开始填砂，并始终保持管廊结构稳定，采用“落雨法”自然倒落；填砂到距离管廊结构模型顶部10 cm时，撤掉辅助工具；此后，继续均匀落砂，直至模型箱顶。

图4 模型箱图

1.1.4 加载测试

将设计完成的管廊模型放置于模型箱内，模型底部与模型箱底部相接触，周围依次填土。 先将管廊结构放置在模型箱内，后填砂到模型箱顶后，依次放置加载板，在其中心逐级加载至75 kg。 加载系统示意图如图5 所示。

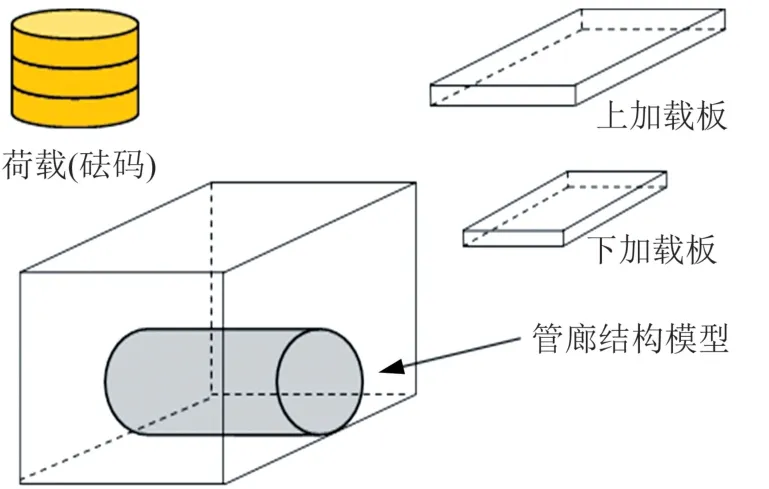
图5 加载系统示意图

在管廊结构模型的上部，砂土中心位置面积为20 cm×20 cm 的区域，依次放置两块加载板，小加载板直接接触砂土，大加载板尺寸为30 cm×30 cm，放置于小加载板上部，便于放置加载砝码。 大小加载板中心校准，校核加载板水平无偏心；用5 kg 砝码进行预压；在加载板的中心位置施加荷载，分级加载，每级10 kg，最大至75 kg，读取4 个百分表显示的最终沉降量。 观测点位置如图6 所示，其中黑点为观测点。试验后取出管廊，观察管体变形或破坏形态。

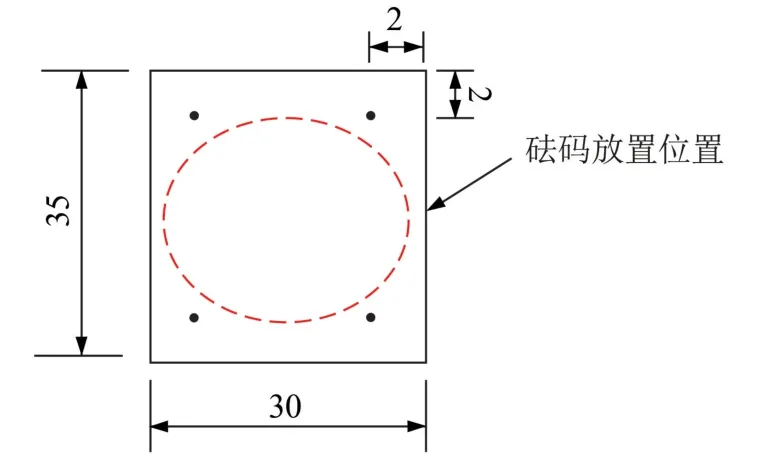
图6 观测点位置图/cm

1.2 结果与分析

根据试验所得到的每级荷载下的土体沉降数据，采用数据处理软件生成折线图，如图7 所示，载荷可分七级，其中初始荷载为5 kg，每级10 kg，逐步加载至75 kg。

图7 新型管廊结构位移—荷载折线图

由图7 可知，表面位移量随着荷载的增大而增加。 在15～55 kg 加载阶段，随着荷载增加，位移量由1 mm稳定增大至6 mm，而且线段斜率保持不变，稳定为0.1，浮动较小，变形量增长较快。 随着每级压力的增大，管廊结构上部的土体先进行自压缩，产生一定的沉降量，结构本身产生一定的弹性变形，土的压缩速度大于结构变形速度，从而使整体产生位移的速度加快。

荷载达到55 kg 时，测得位移值为6 mm，在65 kg时土体沉降为8 mm，此曲线斜率较大，斜率值逐渐增大至最大值，其值为0.2；土体与管廊结构体的位移变化速度加快，在65 kg 时位移达8 mm，土的压缩速度等于结构的变形速度，管廊结构本身变形达到弹塑性阶段，到达某个临界点时，土体与管廊本体产生协同变形，结构结束弹塑性变形，推测下个阶段的管廊结构将可能产生塑性变形。

在65～75 kg 加载阶段，曲线斜率＜0.1，显示变形减缓。 表面结构体继续受力，同时上部砂土层逐渐密实，土体压缩速度越来越小，可压缩的土量越来越少，结构变形速度开始大于土体压缩速度，此时变形量主要来源于管廊结构承担上部荷载时的形变量，曲线的斜率约保持在0.8，结构具有一定的稳定性，荷载加载完毕后，土体和结构共同承担荷载，土体压缩与结构形变量叠加为总位移量，其最大值为8.6 mm。

采用图形处理软件，可得到土体位移等值线如图8 所示，可直观看出，影响范围以加载板区域为中心向四周区域扩散。

图8 “沉降盆”—土体位移等值线图/cm

土层表面位移量集中于中央横坐标为20 ～40 cm、纵坐标为10 ～30 cm 处，其中受荷位置的土体变形沉降量大，位置在横坐标为25 ～35 cm、纵坐标为15～25 cm 的加载板处，其最大值为0.8 cm，等值线较密集；加载板以外区域的土体变形沉降量小，其最小值为0.01 cm，等值线越来越稀疏，代表了荷载影响越来越小，逐渐减至0 cm。

如图8 所示，沉降主要产生在中心区域的加载板以下部分，荷载对于模型周边荷载外围区域的土体产生的影响随着距离的增加而减小，一定程度上反映了地基土的压缩变形理论。

2 翼式地下综合管廊受力性能数值分析

基于管廊加载的模型试验，采用大型通用有限元计算软件ABAQUS，分别对管廊模型在均布荷载作用下的上部土体沉降与模型受力两部分进行数值分析，以进一步研究薄壁摩擦型管廊的受力性能，探寻数值分析与试验数据之间的关系。

2.1 有限元模型

2.1.1 网格模型

在数值模拟软件中，土体模型采用非摩尔库伦模型的弹性模型，作为三维立体模型，土体采用适用于三维应力的十节点二次四面体(C3D10)单元进行模拟，7 897 个节点，4 790 个单元，较好地反映了土体的受压过程，土体网格模型如图9(a)所示；管廊结构采用八节点减缩厚壳(S8R)单元，二次四边形技术，建立内部管廊结构网格，节点数为5 602、单元数为2 680，管廊网格模型具体划分如图9(b)所示；锚杆模型采用六面体技术映射网格，20 节点二次六面体(C3D20)进行单元划分，共有3 354 个节点、420 个单元，锚杆网格模型示意图如图9(c)所示。

图9 管廊结构加载网格模型示意图

2.1.2 材料属性

土体采用常规实体单元，弹性体。 管廊结构和锚杆单元分别采用壳单元和实体单元。 材料设置力学参数见表2。

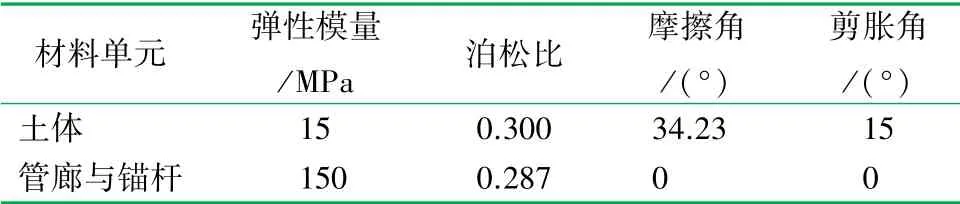
表2 材料属性表

2.1.3 荷载与边界条件设置

依据所施加荷载进行换算，可得土体顶面施加局部压应力大小分别为36、60、84、108、132、156 和180 kPa等7 级荷载，进行不同荷载状况下的模拟。同时设置土体地应力的大小为-18 kN/m3，其方向用u3表示。

边界条件为顶部无约束。 设置土体四周的约束:(1) 限制4 个竖向平面x、y方向的位移；(2) 在底面设置x、y、z3 个方向的约束，限制其位移。

2.2 结果与分析

2.2.1 模拟结果分析

土体变形俯视图如图10 所示，变形集中在其中心加载部位，对于其周边区域影响较小，最大位移为8.6 mm，最小位移为2.9 mm；沉降区域分区更加详细，根据不同颜色，由深色到浅色可分为5 级区域，分别是8.598 ～7.882、7.882 ～7.165、7.165 ～6.449、6.449～5.732和5.732～5.016 mm。 土体最大位移变形量在中心红色区域，其最大值为8.6 mm。 图形模拟结果同上述试验的“沉降盆”结果相似，变形程度以颜色不同作为参考量，土体变形量较大值主要集中于模型中央方形红色区域，荷载对于周边区域的影响减弱，故周边区域变形量较少，颜色较浅。

图10 上部土体变形俯视图

模拟位移最大值点为图10 的中心点，作出该点随着荷载增加的沉降量折线图，如图11 所示。 随着加载过程的进行，上部土体顶点产生沉降，由0 mm开始，逐渐增大。 在初始施加荷载0～35 kg 部分，形变量的增加量较小，形变较为平稳；在35 ～65 kg 区域，沉降值由2.5 mm 增大到7.8 mm，其增加量为5.3 mm，而折线斜率＞0.1，与图5 结果较为相似，二者沉降变化率保持在0.1 ～0.3。 进入最后一阶段，位移量由7.8 mm 增长到8.6 mm，其增长量为0.8 mm，在结构承载提高的情况下，形变量的增长率＜0.1，也与图5 所得结果有着密切联系。

对管廊结构主体受力结构分析表明，管廊的最大变形量也集中于中心浅红色部位，管廊顶部变形俯视示意图，如图12 所示。 位移最大值主要集中于结构的中心区域，同图10 的结果相似，也根据不同颜色，由深到浅可分为5 个区域，分别为8.184 ～7.521、7.521～6.857、6.857 ～6.194、6.194 ～5.530 和5.530～4.867 mm。 间接表明管廊结构与土体之间协同受力与变形关系。 管廊结构初始形变量为0 mm，加载开始后，随着荷载增加，逐渐增大到最大值8.18 mm。

图11 土体位移—荷载折线图

图12 管廊顶部模拟变形俯视图

2.2.2 试验与模拟结果对比分析

管廊结构试验与模拟结果对比曲线如图13 所示，两条曲线的沉降初始值从0 mm，逐渐增长到最大值，增长趋势相同；在15～45 kg 的荷载范围段，试验所得数据的值大于模拟所得数据值，其最大差值为1 mm；在55 kg 时，模拟值大于试验值，此后二者数值虽有差异，但误差较小，模拟值逐步增大至最大值8.60 mm，试验值的最大值为8.17 mm，模拟值与试验值之间的误差为5%，验证了试验的合理性。

3 结论

通过综合管廊结构的受力试验与数值分析，得到的主要结论如下:

(1) 在管廊结构体上部施加实际工程荷载的工况下，新型管廊结构试验的变形值约为8.17 mm(＜10 mm)，满足了变形与沉降控制标准；模型整体沉降随着加载的增加而依次提高，沉降速率从试验开始时的匀速到最后的平稳阶段，斜率约保持在0.1。

(2) 新型管廊结构模型土体模拟整体最终沉降值为8.60 mm，管廊结构模拟形变最大值为8.18 mm。 较好地验证了新式管廊体的抗变形能力，综合管廊的外伸支撑锚杆体与管廊协同受力变形，并且与土体产生的摩擦效果，较好地减缓了沉降变形速率，在平衡土体重力与外加荷载时起到重要作用。