把握立体几何问题的本质 培养与发展直观想象能力
李子超


[摘 要]高中立体几何是提升直观想象核心素养的重要载体.文章以棱锥的外接球问题为例,分析解决立体几何问题的本质:以长(正)方体模型为基础、以立体图形平面化为核心、以几何问题代数化为手段,而促进学生突破问题难点,培养与发展学生的直观想象能力.
[关键词]立体几何问题; 直观想象能力;棱锥;外接球
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2021)11-0027-03
一、问题的提出
高中数学课程标准确定了高中数学核心素养的6个要素:数学抽象、逻辑推理、数学建模、直观想象、數学运算、数据分析[1].直观想象是指借助几何直观和空间想象感知事物的形态变化,利用图形理解和解决数学问题的过程.立体几何是培养和发展学生的几何直观能力、运用图形语言进行交流的能力、空间想象能力与一定的推理论证能力的很好的素材[2].而棱锥的外接球问题,更能全方位、多角度、深层次地培养与发展学生的直观想象能力.
在实际教学中发现,很多学生在学习“棱锥的外接球问题”这一内容后,感觉问题抽象难以理解.究其原因是,这类问题结合多个几何要素,空间位置关系较为复杂,加上学生对曲面图形的直观感觉较差,所以觉得问题抽象难以解决.
本文以棱锥的外接球(如果一个棱锥的所有顶点都在同一个球面上,那么这个球就叫作棱锥的外接球)问题为例,分析解决立体几何问题的本质,从而促进学生突破问题难点,培养与发展学生的直观想象能力.
二、立体几何问题的解题本质
立体几何主要研究现实世界中物体的形状、大小与位置的关系. 通常采用直观感知、操作确认、思辨论证、度量计算等方法认识和探索几何图形及其性质[2].下面以“棱锥的外接球问题”为例,分析立体几何问题的解题本质.
1.长(正)方体模型是解决立体几何问题的本质基础
普通高中课程标准实验教科书数学必修2教师教学用书中指出:“……以长方体为载体,使学生在直观感知的基础上,认识空间中点、线、平面之间的位置关系……”[2]由此可见,长(正)方体模型是学习立体几何的基础,对理解立体几何的关系起着重要的作用,尤其是解决棱锥的外接球问题. 由长方体和球的对称性容易得到结论1:
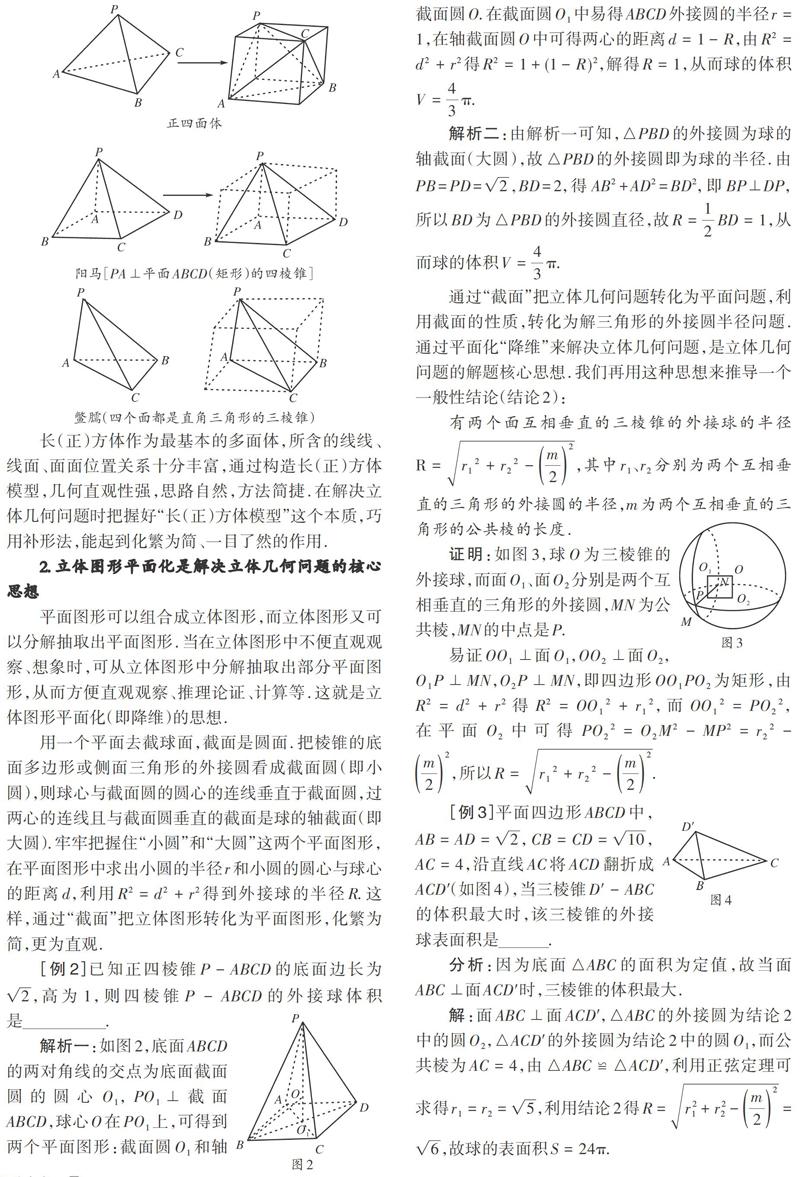
如果棱锥的顶点与长(正)方体的几个顶点重合,那么这个棱锥的外接球与长(正)方体的外接球相同, 可以把棱锥补成相对应的长(正)方体,转化为求对应的长(正)方体的外接球半径.这种方法就是立体几何中常用的“补形法”.
分析:该三棱锥的三组对棱两两相等,恰好与长方体的三组对面的对角线等价,可以三组对棱分别为长方体的三组对面的对角线补成长方体.
另外,常见的可以补成长(正)方体的棱锥还有:
长(正)方体作为最基本的多面体,所含的线线、线面、面面位置关系十分丰富,通过构造长(正)方体模型,几何直观性强,思路自然,方法简捷.在解决立体几何问题时把握好“长(正)方体模型”这个本质,巧用补形法,能起到化繁为简、一目了然的作用.
2.立体图形平面化是解决立体几何问题的核心思想
平面图形可以组合成立体图形,而立体图形又可以分解抽取出平面图形.当在立体图形中不便直观观察、想象时,可从立体图形中分解抽取出部分平面图形,从而方便直观观察、推理论证、计算等.这就是立体图形平面化(即降维)的思想.
用一个平面去截球面,截面是圆面.把棱锥的底面多边形或侧面三角形的外接圆看成截面圆(即小圆),则球心与截面圆的圆心的连线垂直于截面圆,过两心的连线且与截面圆垂直的截面是球的轴截面(即大圆).牢牢把握住“小圆”和“大圆”这两个平面图形,在平面图形中求出小圆的半径[r]和小圆的圆心与球心的距离[d],利用[R2=d2+r2]得到外接球的半径[R].这样,通过“截面”把立体图形转化为平面图形,化繁为简,更为直观.
通过“截面”把立体几何问题转化为平面问题,利用截面的性质,转化为解三角形的外接圆半径问题.通过平面化“降维”来解决立体几何问题,是立体几何问题的解题核心思想.我们再用这种思想来推导一个一般性结论(结论2):
3.几何问题代数化是解决立体几何问题的有效手段
“数”和“形”是不可分割的统一体,数、形相互沟通、相互印证.以“数”研究“形”,把复杂、抽象的几何问题转化为有序可算的代数问题,使得问题有路可循,易于解决.而坐标是几何问题代数化重要的工具,对于许多抽象的立体几何问题,借助坐标转化为代数计算,可实现空间几何代数化,简化复杂抽象的几何关系,从而使问题易于解决.
分析:直线[MN]与球[O]的关系难找,从图形的角度解题较难.根据正四面体的对称性,可尝试把正四面体补成正方体,通过建立空间直角坐标系简化几何关系,从而化解难点.
三、把握立体几何问题的本质,培养与发展学生的直观想象能力
高中立体几何是培养与发展学生直观想象能力的重要载体,在处理这个模块的相关问题时,教师要把握好“以长(正)方体模型为基础”“以立体图形平面化为核心”“以几何问题代数化为手段”这几个立体几何问题的本质,通过转化与化归,培养与发展学生的直观想象能力.
长方体是立体几何最基本的几何体,它不但全面展现了空间点、线、面的位置关系,而且学生较为熟悉,理解掌握得较好,是展开空间想象的重要依托,是研究立体几何问题最基础的模型.在日常立体几何的教学中,教师要把握住“长方体模型”这个基础,通过联想、类比、构造长方体模型,把问题转化为熟知的、形象的、直观的模型,培养与发展学生的直观想象能力.例如,在处理线面、面面平行(垂直)有关定理、性质时,教师要善于引导学生通过长方体模型,把抽象、复杂的位置关系简化在典型、熟知的长方体空间中,以显露内在联系,以简驭繁,培养与发展学生的直观想象能力.
立体几何是平面几何的延伸与拓展,两者相互转化实现内容的补充和问题的解决.选取或构造恰当的平面,使得问题在这个平面上获得突破性进展,甚至全部解决[3],这就是立体几何平面化思想,是研究立体几何问题的核心本质.把握这一本质,教师在立体几何的教学中要有目的地、系统性地渗透立体几何平面化思想,不断强化学生对平面图形的认识和运用,以培养与发展学生的直观想象能力.其实,立体图形的“直观图”就是平面化的一种成果,很多教师在平常的教学中喜欢用“多媒体”等工具让学生“眼观”“空想”,而从不让学生动手画图,这对于学生空间想象能力的培养与发展帮助有限.教师应切实让学生自己动手操作,引导学生在“平面”上体现出“空间”,从而深刻体悟空间关系,培养与发展直观想象能力.
向量和坐标是用代数方式来研究立体几何问题的重要工具,当立体几何问题由于条件隐晦、图形关系复杂、技巧性强、处理难度较大时,可通过向量或坐标系将几何条件转化为坐标的数量关系,通过计算加以解决,使得解决问题的思路变得清晰简单.向量和坐标的运用,既简化了复杂抽象的几何关系,又为解决问题提供了更为灵活的思路和途径,简捷明快,化难为简[4].
[ 参 考 文 献 ]
[1] 史宁中.高中数学课程标准修订中的关键问题[J].数学教育学报,2018(1):8-10.
[2] 刘绍学.普通高中课程标准实验教科书数学必修2教师教学用书[M].北京:人民教育出版社,2015.
[3] 谢晓强.立体几何中的平面化思考[J].数学教学研究,2004(6):13-15.
[4] 陈晨, 沈枫, 宋忆宁,等.用代数方法解决平面几何问题[J].科海故事博览·科技探索, 2014(1):35.
(责任编辑 陈 昕)

