让数学模型的种子在孩子心中生根发芽

摘 要：“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径”。模型是对现实世界中一类相近事物的放大，它源于现实，又高于现实。数学模型思想的建立有助于帮助学生快速从生活事例中看到数学问题，并利用数学模型思想对信息与问题进行分析与重组，达到将复杂的问题简单化，抽象的问题具体化，将学生的思维引向深处，在发展学生思维能力的同时提高学生学习数学的兴趣与应用意识。

关键词：《分段计费解决问题》;思维能力;简单化

数学问题大部分源于生活，但往往正是身边的数学问题，学生才感觉最为陌生，解决起来没有切入点。接下来笔者将以“分段计费问题”为例，从“分析中理解标准、体验中感悟模型、总结中提炼模型、运用中发展模型”几方面例谈小学数学模型思想的培育。

【教学内容】

人教版数学五年级上册第16页。

【教学过程】

一、 抽丝剥茧，在分析中理解标准

师：这是什么场景？李叔叔遇到什么问题了吗？图中有什么关键信息？你是怎么理解收费标准的？请和同桌说说？生：我的理解是如果不超过3km的话，它就是7元，如2.5km就收费7元。

师：1km收费多少？1.1km呢？2km呢？2.1km呢？3km呢？生：只要不超过3km，都按7元算。

师：概括得真好。超过3km的部分，每千米1.5元又是什么意思？生：如4km的话，3km的就算7元，超过的1km就要按1.5元来算，7元加1.5元就等于8.5元。

师：谁也来分享自己的看法？生：如果是7千米，就要分出3km算7元，剩下的4km每千米算1.5元。

师：讲得很具体。不足1km按1km来计算，你又是怎么理解的？生：比如他坐了3.5km，3km就是用7元来计算，剩下的0.5千米按1km的来计算。

师：也就是要算几千米？生：4千米。师：你的理解真到位！师：请和你同桌说说6.3km、3.1km、4.9km 该按几千米计算？生：我发现6.3km要按7km 算，3.1km 按4km算，4.9km按5千米算。

师：也就是所有含小数的里程数，都要用“进一法”进一成整千米的里程数计算。

【思考】针对收费标准，师生之间展开了有目的性的对话，一层一层拨开收费标准后的“关键信息”。在教师的引导下，学生充分发表见解并能自主总结出“3km以内都算7元”“进一法”“从7km里分出3km”等解题关键，对后续正确解决分段计费问题起到了至关重要的作用。分段计费模型涉及了前段收费和后段收费问题，其本质是对行驶里程的分段，计算的是出租车前3km内里程价钱和后3km里程价钱总和。因此在上述教学环节中，为了帮助学生更好地理解3km以内7元，教师通过变式对话学生1km、2km 和3km的具体价钱，同时通过学生对6.3km、3.1km、4.9km 的计费里程讨论，让学生充分理解不同里程的实际计费里程，帮助学生更有效地理解“进一法”的运用意义。

二、 数形结合，在体验中感悟模型

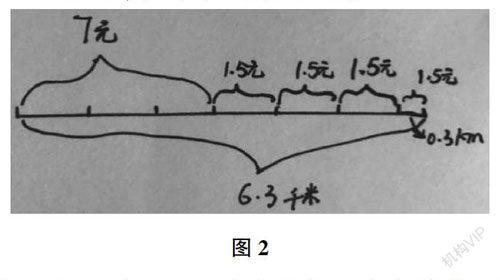
师：你能用画图的方法表示这道题的信息和问题吗？（生画图）生1：从图中（图2）可以看出，前3km按7元算，后面一共有6.3-3=3.3km按4km算，一共有4个1.5元，合起来就是13元。

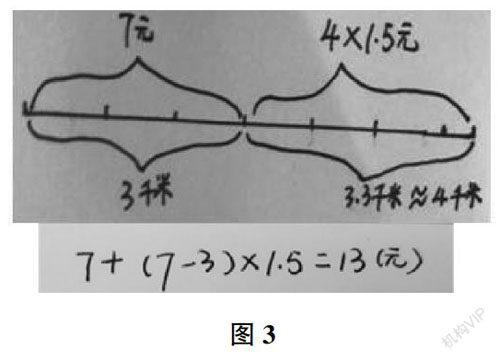
生2：题目说不足1千米要按1千米计算，所以把6.3km进一成7km（如图3）。前3km一共7元，剩下4km每千米1.5元，也就是7+（7-3）×1.5=13元，所以李叔叔要付13元。

师：采用“进一法”，使计算过程更加清晰了。请思考计费过程中分了几段计费，分别表示什么意思？

生：分两段，第一段是7元起步价，第二段是超出3km的收费。

师：所以总费用可表示为？生：起步价加超出的钱数等于李叔叔要付的钱数。

【思考】《数学课程标准》（2011年版）指出：“借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。”在数学学习中，运用数形结合思想可以使复杂、抽象、难懂的数学问题转化成简单、具体、易懂的图形，使隐蔽的数量关系明朗化，帮助学生有效理清问题中的数量关系，继而有效地解决问题。学生在画一画的体验活动中能够直观具体看清出租车的分段计费原理，降低学生学习难度。在师生交流互动过程中，交流、对比、讨论出分两段计费的收费模型，即前3km费用+超出里程费用=李叔叔要付的总费用，实现从图突破，建构分段计费模型结构的目的。

三、 发现规律，在总结中提炼模型

（生独立填写书本第16页表格。）

师：请同学们观察表格中的数据，行驶里程和出租车费之间有什么关系？生：3km以内只要7元，以后每增加1千米增加1.5元这样子的规律。

师：是什么引起了出租车费用上涨呢？生：是路程引起了出租车费用的增加。

师：请看下面的表格，通过观察4km、5km、6km的计费算式，你发现了什么？

生1：我发现都要把前面3km的7元加上。生2：我发现费用总价等于7元加上超过3千米的里程费用。

师：说得真好，用3km的起步价7元加上超过3km部分的里程就等于总费用，你能接着往下说7km、8km的车费吗？出租车费会随着行驶里程的增加而增加，根据价格表，看到的行驶里程都是整千米数。师：你能找到6.3km是多少钱吗？生：和7km收费一样，是13元。

师：如果出租车价钱是16元，行驶里程可能是多少呢？生1：可能是9千米。生2：也可能是8.6公里。

師：也就是说，出租车费16元，行驶里程可能在8km 至9km之间，包括9km。

【思考】通过让学生计算出10km以内的出租车车费，让学生自主感受分段计费的模型，通过教师呈现的里程计费算式，学生能清楚看到计费的模型原来就是前段收费加上后段收费，这样的总结形式能让学生更好地理解与记忆分段计费模型。此外，交流得到出租车费会随着行驶里程的增加而增加，这与前文所说的分段计费其实是里程的分段收费相呼应。在总结环节，教师通过展现分段计费的算式结构，让学生识记分段计费的基础模型，有助于夯实学生对于分段计费模型结构的认知。

四、 举一反三，在运用中发展模型

练习一：某市自来水公司为鼓励节约用水，采取按月分段计费的方法收取水费。12吨以内的每吨2.5 元;超过12吨的部分，每吨3.8元。

（1）小云家上个月的用水量为11吨，应缴水费多少元？（2）小可家上个月的用水量为17吨，应缴水费多少元？

（学生汇报解答过程。）

师：观察例题与练习题，这两题的收费标准与解答过程有什么异同？生：出租车是3km以内7元，而水费是12吨以内每吨2.5元，是不一样的。两题都是分段计算的。

师：既然都是分段计费的问题，我们就要找准分段的分界点。这题的水费12吨以内每吨2.5元，所以是需要计算的。

练习二：（如图5）

师：你怎么理解合影价格表的？生：我的理解就是27.5元包括5张照片，超过5张每张2.5元。

师：也就是前5张27.5元，超过部分每张2.5元。怎样列式呢？生：27.5+30×2.5=102.5（元）

【反思】通过生活中常见的水费收费和照相收费问题，让学生在变式中找相同点与不同点，在运用中明晰并不是所有分段计费问题的模型都是统一不变的，在实践中发展学生学习分段模型的同时，培养学生思维的灵活性，提高解决问题的能力。

在画一画的环节当中，个别学生出现了如图6的做法，表现出了学生思维的灵活性，但在新课当中这种“补差价”的方法只有部分学生能够理解，因此，为了不干扰学生分段计费基本模型的建立，笔者对教材进行重组与设计，将第二种方法作为课堂的生成资源，在第二节练习课进行交流。因此我们在尊重教材的基础上也要根据学情合理设计教学活动。

数学源于生活，却不止于生活，让孩子把身边的数学学活是一件不容易的事情，把数学模型的种子播撒在孩子的心间更是一件值得万千教师努力的事，在课堂教学中，教师若能时刻关注学生，立足教材，时刻不忘数学模型思想的培育与指导，我们的学生将会成为更适合社会发展的全面发展的人。

作者简介：

林晓妮，广东省东莞市，东莞市东城花园小学。