基于自调节深度信念网络的入侵检测算法
逯 玉 婧
(石家庄职业技术学院 人事处,河北 石家庄 050081)
随着云计算、工业互联网、5G等新兴技术的发展,网络安全风险呈现出海量、高维与叠加的趋势,网络安全防护面临新的挑战.入侵检测是一种主动的网络安全防护技术,目前该技术仍然为研究的热点.但是,传统的入侵检测技术已经难以满足新时期网络防护的需要,因此,探索出适应新时期互联网环境的入侵检测技术具有重要的意义.
当前的入侵检测技术研究主要围绕机器学习算法展开,学者们提出了一些行之有效的入侵检测算法.文献[1]提出了一种结合改进粗糙集属性约简和K-means聚类的网络入侵检测算法,使用它可以缩短入侵检测的时间;文献[2]提出了一种改进的正则化极限学习机入侵检测算法,该算法采用天牛群优化算法对权值和阀门进行联合优化,提升了入侵检测的准确率;文献[3]提出了一种基于合成少数类过采样技术(SMOTE)和深度信念网络(DBN)的入侵检测算法(SMOTE-DBN),该算法能够提高对少数样本的检测准确率;文献[4]提出了一种自适应遗传算法,通过搜索获取最优特征子集,具有较好的检测效果.这解决了一部分入侵检测算法的不足,但仍然有一些问题尚待解决,例如,算法参数过多,调优困难;算法容易陷入局部最优;当遇到网络攻击类型多的情况时,算法的误报率较高等.
针对当前入侵检测算法存在的部分问题,本文提出了一种自调节深度信念网络入侵检测算法(Self Adaptation Deep Belief Networks,简写为SADBN).该算法在网络数据特征提取过程中,从统计力学角度出发,依据受限玻尔兹曼机(Restricted Boltzmann Machine, 简写为RBM)能量的变化进行算法调优,使得入侵检测算法具有全局性与稳定性.为提高少数攻击类型的检测准确率,本文结合集成算法的思想,将DBN学习到的特征输入到随机森林中进行训练,得到了入侵检测算法的模型.
1 基本概念简介
1.1 DBN
DBN是由若干层无监督的受限玻尔兹曼机与有监督的反向传播网络(Back Propagation,简写为BP)构成的.它的训练模型分为预训练和微调两部分.在预训练阶段,DBN采取逐层训练方式对每一层的RBM进行训练,下层RBM的输出值将作为上层RBM的输入值;在微调阶段,该模型使用BP神经网络(一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一)进行有监督的学习,并对整个DBN权值进行微调.DBN网络结构示意图见图1.
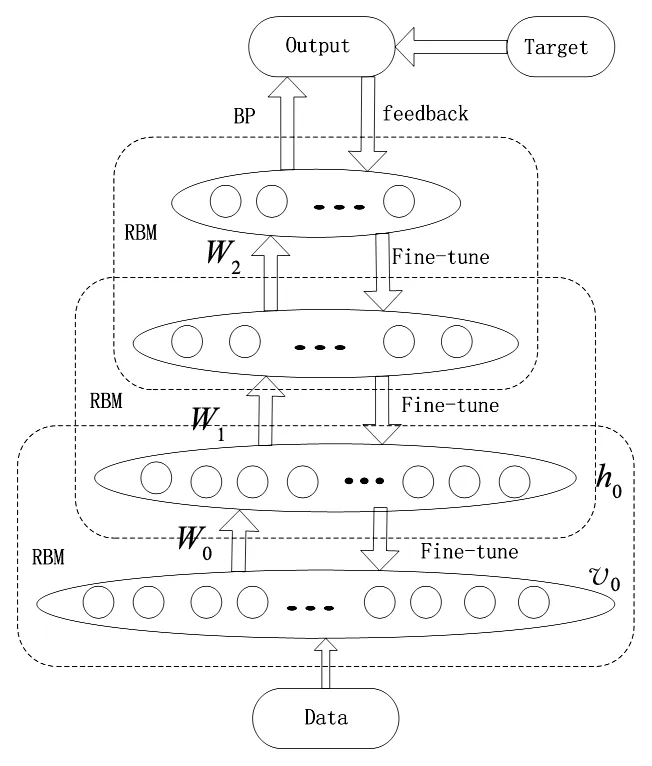
图1 DBN网络结构示意图
1.2 RBM
深度信念网络的主要组成部件为RBM.RBM是一种具有两层对称结构的随机神经网络模型[4],其模型见图2.
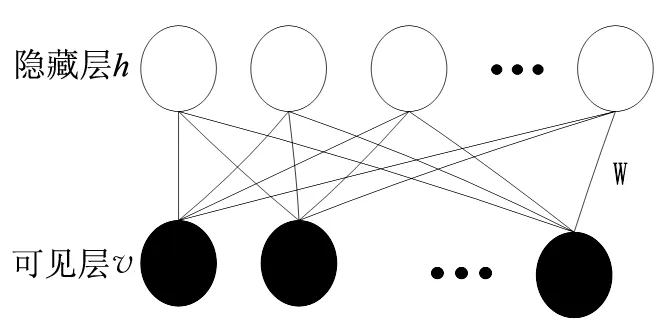
图2 RBM模型图
RBM由一个可见层和一个隐藏层构成,层间连接方式采用全连接,层内连接方式采用无连接,图2中v为可见层;h为隐藏层;W为可见层与隐藏层之间的连接权重.如果可见层与隐藏层之间的权重矩阵表示为Wm*n,可见层节点的偏置量表示为a=(a1,a2,…,an),隐藏节点偏置量表示为b=(b1,b2,…,bm),假设每个节点允许在集合{0,1}进行取值,第i个可见层节点状态为vi,第j个隐藏层节点状态为hj,则网络状态为(v,h)时,RBM能量函数计算公式为:
E(v,h|θ)=
(1)
公式(1)中,θ={Wij,ai,bj}作为RBM的参数,Wij为可见层与隐藏层之间的连接权重,ai为可见层的偏置,bj为隐藏层的偏置.当参数确定时,通过该能量函数得到(v,h)的联合概率为:
(2)
公式(2)中,Z(θ)为归一化因子.
似然函数表示为:
(3)
通过贝叶斯公式可以推导出隐藏单元和可见单元的激活状态.因此,第j个隐藏单元的激活概率为:
P(hj=1|v,θ)=σ(bj+∑iviWij)
(4)
第i个可见单元的激活概率为:
P(vi=1|h,θ)=σ(ai+∑jhjWij)
(5)
RBM的学习目的是求解参数θ的值,进而拟合目标数据.假设T为训练样本的个数,似然函数为:
L(θ|v)=∏Tp(v(t))
(6)
对L(θ|v)求对数后,继续求导数,可得:

(7)
由公式(3)可得:
lnp(v(t))=
ln(∑he-E(v(t),h))-ln(∑v,he-E(v,h))
(8)
将公式(8)代入公式(7)可得:
(9)
分析公式(9)可知,p(h|v)表示可见层与隐藏层的联合概率分布情况,需要遍历v所有的值.DBN中RBM采用的是对比散度快速学习算法[5].该算法与Gibbs采样算法略有不同,它在已知样本初值状态v0时,就可以通过较少的抽样步数达到较好的近似目标样本分布效果[6].
2 SADBN算法
2.1 算法思想
RBM是一种以统计力学为基础, 引入了能量函数的随机网络.为了方便描述,将RBM能量函数定义为Costsystem=‖Eε(vi,hi)-Eη(vi,hi)‖,其中,Eε(vi,hi)为初始学习率ε下RBM的能量,Eη(vi,hi)为测试学习率η下RBM的能量.RBM系统的能量是固定的.根据最小自由能量原则,当RBM中的自由能量达到最小状态时,RBM可以达到稳定状态,此时处在一个概率集中且有序的状态中.因此,在RBM中引入退火算法可使能量经过多次转移,达到一个最低的稳定状态.该最低稳定能量下的学习率η为最优点的学习率.通过多次训练RBM,并将原始入侵检测数据进行重构,就能抽象出高级的入侵检测特征.将该特征输入到随机森林分类器中,就可进行模型训练与预测识别.
2.2 算法步骤
该算法可以分成两部分进行描述.算法一描述SARBM(Self Adaptation Restricted Boltzmann Machine的简写)的训练过程,该算法主要用于实现RBM中参数学习率的自调节寻优;算法二描述逐层对SARBM进行训练的过程,该算法将入侵检测多维度数据进行降维处理,抽象出重要的入侵检测特征,最后提取特征并进行分类.
2.2.1 算法一——SARBM算法
(1)输入
训练样本xi,隐藏层单元个数m,学习率ε,学习空间设置为[c,d],最大训练周期为N,SARBM模型参数θ={tW,a,b},其中,1=t1 (2)输出 W,a,b (3)训练阶段 初始化:vi=xi;W,a,b初始化为随机小的数值. Forτ=1∶N Forp=1∶M 采样:(vi,hj)=((v1,h1),(v2,h2),…,(vn,hm)). 交换:计算每条温度链之间相邻的温度数值.满足温度交换条件时进行跳转.取t=1时参数θ的数值. End 按照下式更新各参数: Eε(vi,hi)= [p,q]←[c+ε,d+ε] For [η=p:q] 按照下式更新各参数: Eη(vi,hi)= Costsystem=‖Eε(vi,hi)-Eη(vi,hi)‖ End 按照下式更新各参数: End 2.2.2 算法二——SADBN算法 SADBN算法是由若干个SARBM模型堆叠而成的.一个N层的SADBN算法可分为4步. 第一步:将入侵检测数据输入到SARBM算法后,逐层训练一个N层SARBM模型,获取抽象表达的特征. 第二步:取出训练好的特征数据组成入侵检测数据集. 第三步:将该数据作为随机森林分类器的训练数据,训练分类器. 第四步:训练好分类器后,将入侵检测的测试数据输入到算法中,进行攻击预测. 实验采用NSL-KDD数据集(入侵检测数据集),训练数据为125 973条,测试数据为22 544条.该数据集中包含的攻击类型有DOS,Porbing,R2L和U2R.为了验证算法的稳定性,对数据集NSL-KDD采用随机算法进行抽样训练入侵检测算法,分别抽取数据的10%,50%和80%. 采用国际上通用的入侵检测技术评价指标——检测率和误报率来进行实验的有效性检测. 为了验证SADBN算法的有效性,采用BP算法、SVM算法、DBN算法和SADBN算法分别进行验证.SADBN算法采用3层的RBM结构进行训练模型,每层的节点数分别选择为30,60,80,随机森林的颗数为30.检测结果见表1. 表1 入侵检测结果对比 /% 由表1可以看出,随着数据量的增加,各类算法的检测率升高,误报率降低.这是因为入侵检测数据越大时,机器学习算法学到的特征越准确,入侵检测算法的模型可以得到很好的训练.在同类入侵检测算法中,SADBN在检测率上高于其他算法.SADBN在特征提取阶段,采用能量变换的方法,使得算法学习特征的能力较强.由于SADBN采用了具有集成思想的随机森林进行分类,误报率与同类算法相比较低. 当面对海量入侵检测数据时,利用SADBN可以迅速从海量信息中抽象出最具价值的特征.与常用的几种入侵检测算法相比,SADBN具有较高的检测率.但是,入侵检测数据集是一个极度不平衡的数据集,针对少数类型攻击的检测,SADBN还需要进一步提升检测率.3 实验与分析
3.1 实验数据集
3.2 实验采用的指标


3.3 结果分析

4 结语

