一种FlexRay网络信息流调度算法研究

王 彤

(航空工业西安航空计算技术研究所，陕西西安710065)

0 引言

FlexRay作为一种灵活的车载网络系统，具有高速、可靠、安全等特点[1]。在实时性的安全网络中，由于节点间的信息交换途径的改变会对网络通信效率和网络性能产生重要影响，因此车载网络的信息流调度算法是改善网络性能的关键，一个好的调度算法不仅能够保证网络通信的有效性，而且可以合理的分配网络资源，更有效的控制由系统引起的时间延迟。基于蚁群算法的资源调度策略可以缩短整个任务的完成时间，维持网络负载平衡，从而提高网络资源的利用率和整体性能，具有可行性。

1 FlexRay通信模式

FlexRay的通信是在周期循环中进行的。一个通信循环始终包括静态段和网络闲置时间，还可能包括动态段、符号窗口。本文主要研究静态段和动态段。静态段和动态段由时隙构成，通过时隙传输帧信息，时隙经固定的周期而重复。

1.1 静态段

FlexRay的静态部分是基于TDMA机制，用于确定的周期性数据通信。FlexRay将静态段分成若干个大小相等的时隙，每个节点都分配了一定的传输时隙，且根据对带宽要求分配了所需时隙的大小。

1.2 动态段

动态段用于触发的实时性非周期性消息的传输，其可用带宽可被动态分配。如果没有节点需要传输消息，则节点等待的时长为一个最小时隙长度；当某个节点时隙计数器读数增加时，节点就会检查对应时隙里是否有准备好的消息需要发送。若有则发送节点会将此消息发送出去，直到这一消息被完全接收之后，动态段内的时隙计数器的值会加1，这个过程循环往复，直到结束。

2 基于蚁群算法的调度算法

2.1 传统蚁群算法局限性

蚁群算法是一种通过模拟蚂蚁觅食从而找到最优路径的方法[2]。传统蚁群算法没有考虑到带宽、时延等约束条件，在解决本文的问题上具有一定局限性，而改进后的蚁群算法将信息素的更新应用到网络路由中，使用每轮迭代更新的信息素的浓度增量来反映服务的质量，解决了传统的蚁群算法在该问题上的不足。

2.2 基于网络路由的蚁群算法

网络路由优化问题[3,4]，即找到一条路径，满足丢包率约束和带宽约束[5,6]。

其中，网络延迟、带宽限制和丢包率约束表示如下：

(1)

bandwidth(PT)=min(bandwidth(e,n∈PT)).

(2)

(3)

上述公式中，PT表示具有处理和转发功能的网络节点和网络中链路的集合;delay(PT)表示网络节点和链路延迟；bandwidth(PT)表示带宽限制；packet_loss(PT)表示网络丢包限制。

基本算法：首先，在基本蚁群算法的基础上，根据上述约束删除掉不满足条件的点和边。其次，在网络中找出经过所有节点并满足约束条件的最优路径，达到保留带宽和时延最小的水平。最后，根据蚂蚁周游后得到的最优路径集合中的链路增加信息素，对其他路径上的链路减少信息素，然后进行下一次迭代，直到迭代次数的最大值。

2.3 静态调度算法

在这里采取了蚁群优化中的一种元启发式算法——频率广义分配问题进行网络资源的分配和调度。

2.3.1 算法描述

假定整个FlexRay通信系统中共有n个通信节点(其中，源节点和目的节点已经确定，并且对于通信网络中的每一个节点都有可分配的时隙)，将FlexRay的一个通信周期分成M个大小相同的时隙。把每个节点作为一个顶点，当两个节点有数据交换时，其间存在一条边，反之则没有边。节点在通信过程中都会被分配一个时隙，被分配了时隙的链路才能够实现两端节点的通信。设系统中的蚂蚁数目为m，每个蚂蚁代表一个资源调度方案，以此为网络中的每个节点选择一个时隙分配。静态消息的调度算法就是寻找到第一个可以用于消息传输的时隙，并能最大化静态段的通信带宽的利用率。

1) 路径选择

概率选择方式使用近似非确定性树搜索的概率计算方法：

(4)

其中,τij表示时隙分配给节点i的信息素量;ηij表示从时隙配给节点i的启发信息；ζ是一个参数，用来规定信息素与吸引力之间的相对重要性;allowedk表示蚂蚁k给节点i满足约束条件的可分配的时隙集合。

当蚂蚁k遍历到节点i时，从可分配的时隙集合中选取一个时隙分配给节点i，并修改禁忌表，更新可分配时隙集合，然后依次遍历下一个节点，当蚂蚁k遍历完所有节点后，可形成一个时隙的分配方案，从而能获得本次遍历的最短时延的节点序列。当所有的蚂蚁都完成节点搜索任务后，即经历一次迭代过程，形成n个时隙分配方案，组成本次迭代可行方案，根据最小时延原则，从本次迭代产生的最优解添加到最小时延集合中，作为当前最优解，并更新集合中的最小时延。当达到最大迭代次数时，选取集合中的最小时延，即为最终解。

2) 局部更新

由于信息素的挥发，当所有蚂蚁在走完一步或者遍历完n个节点，即在一个循环的结束，要更新残留信息素。根据公式：

τi,j(k+1)=(1-ρ)*τij(k)+Δτi,j.

(5)

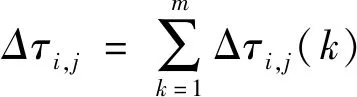
(6)

其中ρ为信息挥发系数;Δτi,j(k)为第k只蚂蚁在本次循环中洒在(i，j)上的信息素增量。

(7)

Q为信息素强度，反映算法的收敛速度，Lk表示第k只蚂蚁在本循环中所有节点和边的和。

3) 全局更新

针对当前全局最优解所属的边按下式进行更新：

τi,j(t+n)=ρ*τ(t)+(1-ρ)*Δτ(t).

(8)

(9)

2.3.2 算法步骤

1) 初始化网络节点ECU_i(i=1，2，……)构建图，生成网络模型节点信息。根据链路的信息，求出网络拓扑结构的邻接矩阵；

2) 初始化信息素浓度：初始化路径(i，j)位置上的信息素浓度与本次迭代在该位置上留下的总的信息素的量。为每条边的信息素浓度设置一个初始值；

3) 根据丢包率、带宽约束删除不满足条件的节点和链路，避免为丢包率过大或者浪费带宽的链路分配时隙，把网络过滤成一个新的网络；

4) 将m只蚂蚁随机放到n个节点上，即选择了第一个可被利用的时隙，将循环次数置为0，初始化禁忌表；

5)m只蚂蚁按概率函数公式(8)选择下一个可用于消息传输的时隙，完成各自的周游；

6) 当蚂蚁k遍历到节点ECU_i时，从可分配时隙集合中选取一个时隙分配给ECU_i，修改禁忌表指针，将被分配到时隙的链路(i，j)添加到蚂蚁的禁忌表之中；

7) 当遍历完所有节点，跳转执行第8)步；

8) 根据公式(7)更新信息素；

9) 当循环次数到达最大值时，循环结束，输出结果。

2.4 网络负载均衡蚁群算法—动态调度算法

在一个特定的时间片内，流经某网关控制节点的流量不规律，网络中资源相对短缺的位置通常会发生拥塞。不均衡的资源分布会增加或调换网络资源。如果使用2.3节所提到的静态调度算法，系统易陷入局部最优，出现早熟停滞现象，无法应对突发的业务量；且易形成网络拥塞，不能达到网络资源的优化配置。

对于网络资源中的负载均衡问题，可以使用调度和负载均衡策略，将负载动态地分配给多个链路。在这里对静态调度算法进行改进，提出一种动态调度算法，使用蚂蚁数量代表网络资源的流量，通过蚂蚁间信息素的相互作用将网络流量分给多条可用路径。以少花费为目标，以当前路径上的信息素浓度为指标选择链路，避开信息素浓度过高的链路，使网络达到最大通过量，尽可能减少时延，把高负载链路上的流量转移到其他较低负载的链路上，减少链路上数据包的丢失。

假设每只蚂蚁代表在链路上传输的数据包，每选择一条链路，都会占用一定大小的带宽。蚂蚁在路径构建的每一步，都根据公式(4)进行时隙分配。每只蚂蚁有一个访问的禁忌表，按照访问的顺序记录已访问过的节点。当所有的蚂蚁都构建完路径后，每条边的信息素根据公式(5)进行更新。

由公式(7)，蚂蚁构建的路径达到最优时，该路径的每条边上就会获得更多的信息素。通常而言，当更多蚂蚁选择一条边时，该边的时延会越短，那么这条边将会获得更多的信息素，在后面的迭代中将会被更多的蚂蚁选择。

3 算法仿真与性能分析

3.1 仿真实验说明以及参数设置

在仿真开始之前，需要对参数进行初步的设置。网络拓扑图如图1。算法设置参数m=150，ρ=0.9、ζ=0.2、Q=100。蚂蚁从原点1、2、3到目标节点6 在节点4处汇合，有四条路径可选：4→5→6，4→6，4→7→6，4→8→9→6，当蚂蚁都选择4→6时，该条路径可能会成为网络的瓶颈，影响网络的性能。

图1 网络拓扑图

用蚁群代表数据包所占用的带宽量，假设每只蚂蚁代表一个基本的网络流量单元Bw=0.2Mb，链路4→6的最大带宽容量为7Mb/s，即最多可以通过35只蚂蚁，当链路上的蚂蚁占用带宽量较多时，不能容纳新选择这条链路的蚂蚁，就会产生丢弃，即在网络中发送丢包的情况。

蚂蚁的数目是150，代表有30Mb的数据包要从源节点4到达目的节点6，如果考虑花费，则都选择最短路径，这样会造成网络的拥塞，丢包率增加。因此，设定一个带宽的限制值，当最优路径到达一定的带宽利用率时，不再运行蚂蚁选择该路径，而是将其分配到其他更好的路径上，提高网络资源的利用率。

3.2 网络负载均衡性能分析

最短路由4→6上蚂蚁的数量变化图如图2。基本的蚁群算法在较短的时间内找到了到达终点的最短路径，同时释放信息素，导致转移概率的增加，影响到以后的蚂蚁，使蚂蚁都选择该最短路径，虽然在路径的消耗上进行了优化，但是会造成大量数据包在最短路径的拥塞，引起数据包丢失。而网络负载均衡的蚁群算法可以将最短路径上的蚂蚁控制在一个较低的水平(最大链路容量)，降低丢包率，减少网络拥塞的发生，从而提高带宽利用率。

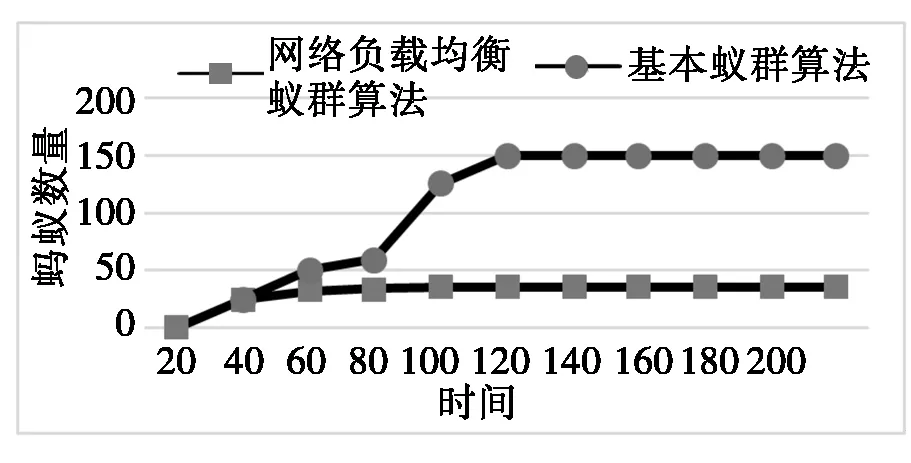
图2 最短路由4-6上蚂蚁的数量变化

网络负载均衡性能实验结果如图3所示。实验结果表明，与基本的蚁群算法不同，网络负载均衡的蚁群算法可以使蚂蚁即网络传输中的数据包更合理的分配到各个路径上，而不是把数据包越来越多地引入最短路径，从而达到网络负载均衡的目的。改进后的蚁群算法将平均带宽利用率从原来的31%提高到70%以上，网络资源的利用率有了很大的提高；将丢包率维持在一个较低的水平，且在较小范围内变化，使网络资源得到合理均衡的分配。从而有效地实现了网络负载均衡，进一步提高了网络的综合性能。

图3 网络均衡性能试验结果

4 结束语

本文从FlexRay总线出发，通过对FlexRay总线及其网络性能的分析，运用保留带宽的思想，研究了基于蚁群算法的静态和动态调度算法并对其进行仿真，为改善FlexRay网络的实时性及性能，提供了理论依据和参考价值。