基于FWD的沥青路面弯沉预测模型对比分析

臧国帅， 金光来

(江苏中路工程技术研究院有限公司， 江苏 南京 211086)

长期以来，我国使用贝克曼梁弯沉仪检测路面弯沉，已积累了大量的实测数据与经验，建立了相关评价标准[1]，但是贝克曼梁(BB)法检测弯沉存在人工操作强度大、效率低等缺点[2]，无法满足城市道路的路网结构强度检测需求。因此发展快速、高效的无损检测技术十分必要。落锤式弯沉仪(FWD)，可以很好地模拟路面实际行车荷载作用，数据量测系统速度快、精度高。

目前，国内外学者对基于FWD预测静态弯沉进行了大量研究，研究表明FWD弯沉与BB弯沉之间具有良好的相关关系[3-7]。郑元勋等[8]发现落锤式弯沉仪稳定性高，且能较好地模拟行车荷载，FWD弯沉与BB弯沉的相关性受试验路段结构及地域条件影响较大。郑飞军等[9]发现FWD荷载级位和路基种类对FWD弯沉与BB弯沉的相关性有影响。孙璐等[10]针对路基弯沉，基于回归分析及神经网络方法，构建了FWD弯沉与BB弯沉弯沉之间的分析模型，结果表明神经网络模型预测效果最好。

虽然国内外学者对静态弯沉预测模型进行了大量研究，但是并未系统分析检测层位、FWD系统误差、弯沉测试范围等因素对预测模型的影响，且多局限于回归分析模型。本文选取上海市4条典型路段进行弯沉检测，基于实测数据建立FWD与BB的回归分析模型和BP神经网络模型。

1 现场实测弯沉数据

1.1 典型路段选取

依据不同道路等级和路面损坏状况，在上海市浦东新区选择了4条典型沥青路面路段：环龙路(环龙路北园路—环龙路龙阳路)、金科路(祖冲之路—郭守敬路)、高斯路(祖冲之路—郭守敬路)、孙新路(华夏高架路—兰亭路)。

为了建立准确的FWD动态弯沉与BB静态弯沉对应关系，路段选取时应确保路面弯沉变化范围足够大。《公路路基路面现场测试规程》(JTG 3450—2019)规定弯沉标定路段应按弯沉值不同水平进行选取，因此本文选取了弯沉值包含0～20、20～60、60～100、100(0.01 mm)等各种情况的路段进行检测。

1.2 弯沉检测方法

依据《公路路基路面现场测试规程》(JTG E60—2008)[11]中规定，分别进行BB和FWD点对点弯沉测试。具体检测步骤如下： ① 沿着所选路段车道的轮迹带，利用贝克曼梁测定回弹弯沉； ② 标准车开走后，以测点为圆心，用粉笔画一个半径为15 cm的圆，标明测点位置；③ 在标明位置处进行FWD动态弯沉检测，位置偏差不超过30 mm。最终在4条典型路段上共采集了62组数据。

1.3 试验数据预处理

因测试数据受多种因素影响，不可避免地产生误差，需要对测试数据进行残差分析，以剔除异常值。在回归分析中，残差即测定值与按回归方程预测值之差，服从正态分布。如果某一测试数据的残差绝对值大于3倍残差的标准差，则其为异常值。将异常值剔除，对剩余有效数据进行回归分析和建立神经网络模型。

2 回归分析模型

2.1 确定最佳回归模型

图1为FWD弯沉与BB弯沉的测试结果。将通过残差分析确定的异常点(876，1 380)剔除，对剩余的61组有效数据进行回归分析。表1为对FWD弯沉和BB弯沉进行回归分析的线性模型、指数模型、对数模型分析结果，选取最佳回归分析模型。从相关系数可以看出，线性模型的回归效果要

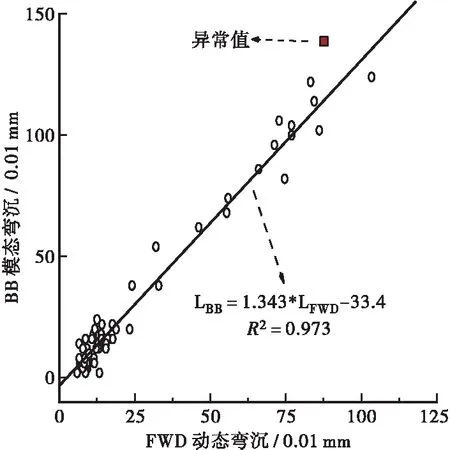
图1 FWD弯沉与BB弯沉相关性分析

表1 FWD中心点弯沉与BB弯沉回归公式模型类型回归公式R2线性模型LBB=1.343 LFWD-33.40.973指数模型LBB=6.61e0.036 5 LFWD0.738对数模型LBB=40.97 ln( LFWD)-179.80.905

显著好于其它两个模型。线性模型的相关系数为0.973，满足规范[11]的要求，表明FWD动态弯沉与BB静态弯沉存在良好的相关性。

2.2 回归模型影响因素分析

2.2.1检测层位

按检测层位划分，弯沉预测模型可以分为面向沥青路面顶面或面向土基。其他研究者建立的回归公式对比见表2。当检测层位为沥青路面顶面时，回归方程的斜率均大于1，这是因为沥青混合料是黏弹性材料，其模量受荷载频率影响显著。FWD荷载为冲击荷载，荷载频率约为25～30 Hz，而贝克曼梁荷载为准静态荷载，因此沥青层在FWD作用时的响应模量远远大于贝克曼梁作用时的静态模量，使得FWD检测弯沉要小于贝克曼梁检测弯沉，表现为回归方程的斜率大于1。

当检测层位为路基顶面时，回归公式的斜率均小于1，这是因为FWD所施加的冲击荷载使土基发生了较大塑性变形，而FWD检测弯沉为总弯沉，包含弹性变形和塑性变形；但是BB检测弯沉采用的是前进法，测试弯沉为回弹弯沉，仅包含弹性变形，最终使得FWD检测弯沉大于BB检测弯沉，表现为回归方程的斜率小于1。所以，基于路面和基于路基所建立的回归方程具有本质差异，应当分别建立回归方程。

表2 不同研究者建立的FWD与BB转化公式检测层位年份作者回归公式相关系数1990唐伯明等[2]LBB=1.327×LFWD-86.50.980沥青路面顶面1993张洪华[12]LBB=1.06×LFWD-160.9101995李锦华等[13]LBB=1.43×LFWD-89.60.9602003樊兆强等[14]LBB=1.34×LFWD-22.990.920土基顶面2010王兵等[6]LBB=0.843×LFWD-8.747 20.9532014郑飞军等[9]LBB=0.728 6×LFWD+17.8260.988

2.2.2FWD系统误差

为了分析FWD系统误差对回归模型的影响，在上文检测数据的基础上，同时使用另一台FWD仪器(记为“FWDII”)在相同位置进行了动态弯沉检测。

表3为FWDII与BB、FWDII与FWD弯沉检测数据回归对比分析结果。由表3可知，FWDII与BB的线性回归公式斜率为1.494，与上文建立的回归公式斜率1.343有较大差异，2台FWD之间的相关系数最高，但斜率并不为1，表明2台FWD检测设备存在一定的系统误差。由于最终将FWD检测弯沉转化为BB弯沉后，再对路面结构承载能力进行评价，而FWD弯沉与BB弯沉之间均具有良好的相关关系，因此FWD设备的系统误差对评价结果影响很小。由此可得：FWD系统误差对回归模型影响较大，而对评价结果影响不大。

表3 不同FWD的回归公式对比检测设备回归公式R2FWDII与BBLBB=1.494 LFWDII-22.10.980FWDII与FWDLFWDII=0.891 4 LFWD-8.70.998

2.2.3弯沉测试范围

随着测试弯沉增大，BB弯沉的人工读数误差对测试结果影响降低，图2为FWD弯沉和BB弯沉之间相关系数随BB弯沉测试范围变化的关系图。由图2可知，随着弯沉测试范围增大，FWD弯沉与BB弯沉的相关系数均急剧增加，而后趋于平缓，接近于1。当BB弯沉测试范围超过0.75 mm时，回归模型的相关系数才能大于0.95，满足规范要求。因此为了得到可靠的转化关系式，应当使得BB弯沉测试范围大于0.75 mm。

图2 弯沉测试范围对相关系数的影响

综上所述，路面结构和FWD系统误差均对回归模型有较大影响，在面对不同用途时，应当分别建立FWD与BB的回归模型；而弯沉测试范围对回归模型的相关系数有较大影响，为了准确预测沥青路面静态弯沉，建立模型所选取路段的弯沉变化范围应足够大。

3 BP神经网络模型

3.1 BP神经网络原理

BP人工神经网络是Rumelhart、McClelland等[15]研究设计，基于误差反向传播算法(Back-Propagation)的一种多层前向神经网络。BP算法是人工神经网络的一种比较典型的学习算法，主要结构包含1个输入层、1个或多个隐含层和1个输出层。各层由若干个神经元构成，每个神经节点输出值由输入值、作用函数及阈值决定，如式(1)所示。神经网络的学习过程包括信息正向传播和误差反向传播两个过程。在正向传播过程中，输入信息从输入层经隐含层传到输出层，经作用函数运算后得到输出值，与期望值比较，若有误差，则误差反向传播，沿原先的连接通路返回，通过逐层修改各层神经元的权值，减少误差，如此循环直到输出结果符合精度要求为止。最基本的3层BP神经网络结构如图3所示[16]。

Oj=fj(Netj)=fj(θj+∑ωijxi)

(1)

式中：Oj为神经元j的输出值；fj为神经元j对应的激发函数；θj为神经元j的阈值；xi表示对神经元j的各个输入；ωij表示对应输入和该神经元j的连接权重。

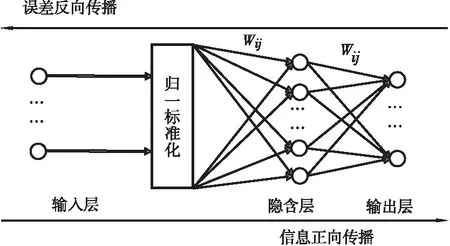
图3 3层BP神经网络结构图

3.2 模型构建与训练

在构建与训练神经网络前，需要对数据进行归一化处理，即将数据映射到[0，1]或[-1，1]或更小的区间。这是因为神经网络输出层的激活函数的值域有限制，如本文采用的双极性S型激活函数，其值域为(-1，1)。因此采用式(2)将数据映射到区间(-1，1)。

(2)

式中：xn为实测数据；xmin、xmax为实测数据的取值范围；yn为实测数据归一化结果。

BP网络具有很强的非线性映射能力，根据Kolrnogorov定理，一个3层BP神经网络能够实现对任意非线性函数进行逼近[17-18]。因此，本文利用商业数学软件MATLAB构建只有1个隐层的3层BP神经网络模型。输入参数为FWD中心点弯沉，输出参数为BB弯沉。训练函数采用LM(Levenberg-Marquardt)神经网络算法，该算法是梯度下降法和高斯-牛顿法的结合，具有梯度下降法的全局特性和高斯-牛顿法的局部收敛性，并通过自适应调整阻尼因子来达到收敛特性，具有更高的迭代收敛速度。

将实测的61组弯沉数据输入到构建的BP神经网络模型中，进行网络训练，然后使用训练好的神经网络进行静态弯沉预测。

4 两种模型预测效果对比

4.1 拟合效果对比

采用均方根误差RMSE(Root Mean Square Error)和平均相对误差MRE(Mean Relative Error)进行模型拟合效果评价，计算公式如式(3)和(4)所示。表4为线性回归和神经网络模型的拟合效果评价结果，从中可以看出，与线性回归模型相比，BP神经网络模型的均方根误差RMSE降低了10 μm，平均相对误差MRE降低了4.6%，表明BP神经网络模型优于线性回归模型。

(3)

(4)

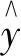
表4 模型拟合效果对比模型RMSE/μmMRE/%线性回归模型5944.0神经网络模型4939.4降低值104.6

4.2 路网结构强度评价结果对比

弯沉预测模型的建立是为了将FWD中心点弯沉转化为BB弯沉，然后依据《城市道路养护技术规程》(DG/TJ08-92—2013)[19]中的贝克曼梁弯沉评价标准，进行沥青路面结构强度评价。沥青路面结构强度可以分为3种状态：足够、临界、不足，为了了解路网整体的结构强度情况，需要统计这3种状态所占的比例，以道路面积作为统计口径。

分别使用线性回归模型和BP神经网络模型对浦东新区2014年路网结构强度进行评价，评价结果如图4所示。BP神经网络模型得到结构强度不足路段所占比例为8.9%，而线性回归模型仅有5.9%，表明使用线性回归模型会使得路网结构强度评价偏于不安全。

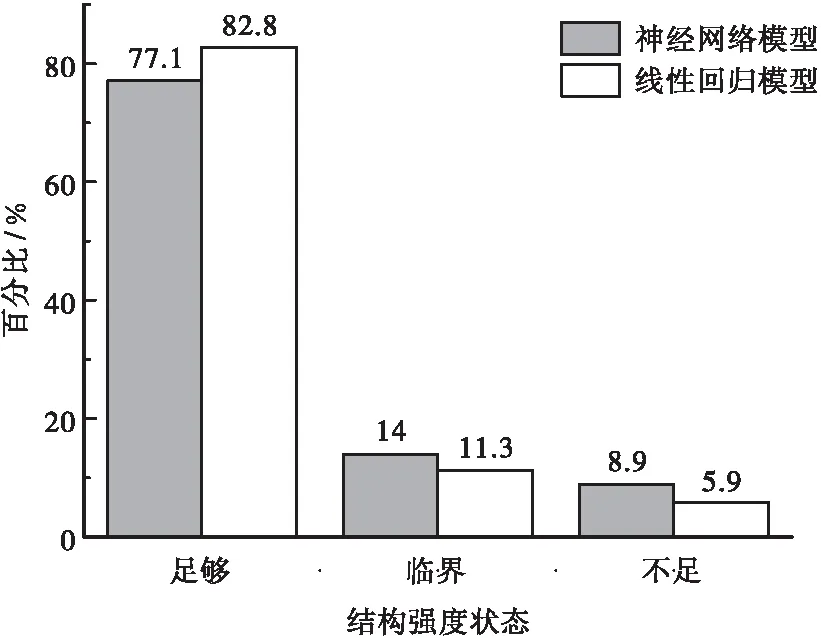
图4 路网结构强度评价结果对比

5 结论

使用FWD和贝克曼梁检测沥青路面弯沉，通过反演对路面的静态弯沉进行预测，建立了道路静态弯沉的回归分析模型和BP神经网络模型。主要结论如下：

1)回归模型的回归系数受检测层位和FWD系统误差影响较大，相关系数受弯沉测试范围影响较大。

2)与回归模型相比，BP神经网络模型的均方根误差降低了10 μm，平均相对误差降低了4.6%，预测效果较优。

3)分别使用两种模型对上海市浦东新区路网结构强度进行评价，结果表明线性回归模型评价结果偏于不安全。

为了准确预测沥青路面静态弯沉，不同检测层位应分别建立预测模型，且选取路段的弯沉变化范围应足够大，并选用BP神经网络模型进行预测。