混凝土二维随机骨料生成和投放的均匀性判别
柯俊宏, 李厚民, 汪 洋, 吴克洋
(湖北工业大学土木建筑与环境学院, 湖北 武汉 430068)
目前, 按照混凝土的研究尺度的不同, 学者们把混凝土研究划分为微观、 细观和宏观三个层次来进行研究。 在细观层次上混凝土材料被认为是由粗细骨料、 界面层、 水泥砂浆、 孔隙以及微裂缝等组成的多相复合材料, 而且多相复合材料的特性对混凝土的非线性宏观力学性能有较大的影响。 目前, 针对混凝土细观问题的实验研究对实验条件要求较高, 如CT扫描仪等设备不易获得[1], 而理论模型的研究相对成熟[2], 如刘家煜[3]基于格构模型对混凝土受拉断裂过程进行模拟, 朱万成[4]采用随机力学特性模型模拟混凝土在单轴压缩作用下的断裂过程,程一磊[5]等采用随机骨料模型模拟三点弯曲试验, 然而现在的随机骨料模型均只考虑骨料位置、 大小和形状的随机性, 忽略了骨料本身的均匀性问题。 因此, 在随机骨料投放程序当中增加骨料均匀性判别手段对其细观力学分析有着重要的意义。
1 二维随机骨料的生成与投放
1.1 骨料级配理论
混凝土内骨料的含量可由Fuller颗粒级配理想曲线公式得出, Walraven运用概率统计的方法, 将三维的Fuller级配公式转换为二维公式, 以此来求得各级配骨料所占的面积, 即:
PC(D
0.0045(D0/Dmax)8+0.0025(D0/Dmax)10]
(1)
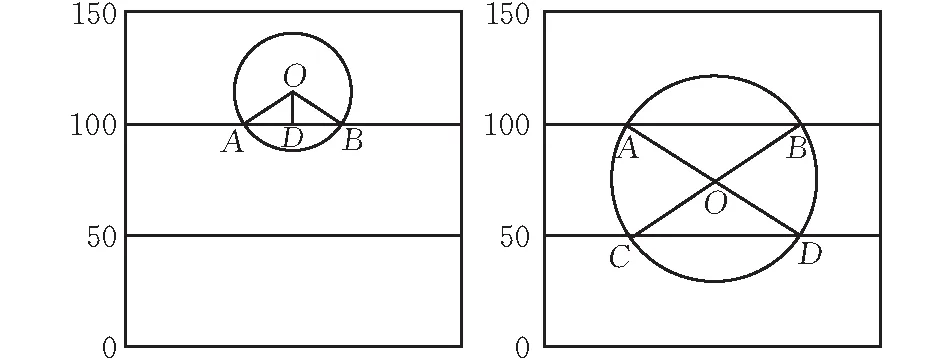
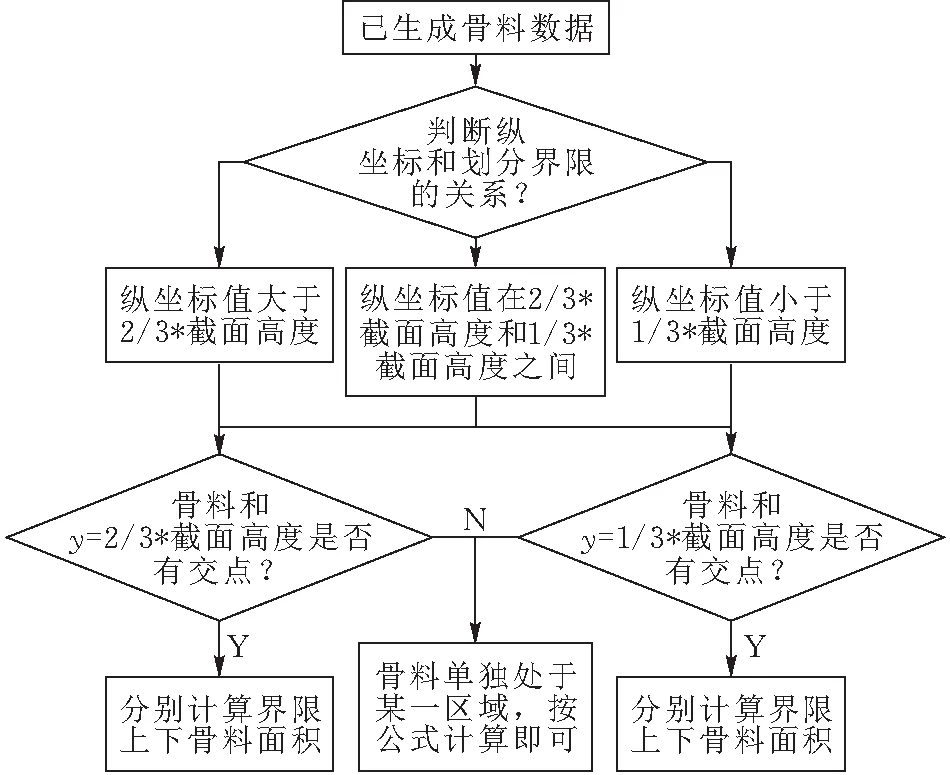
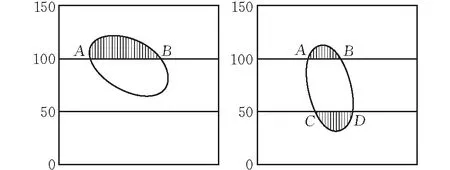
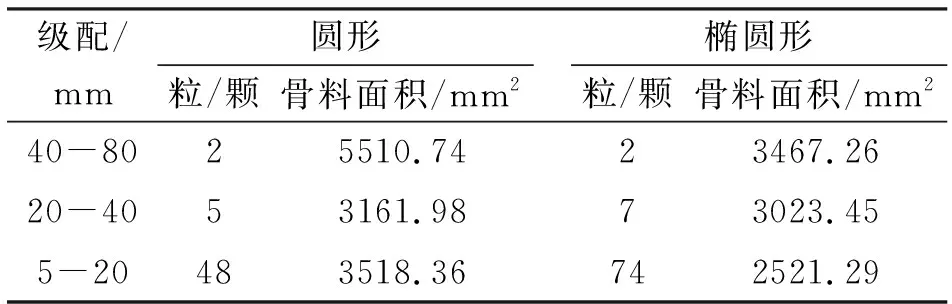
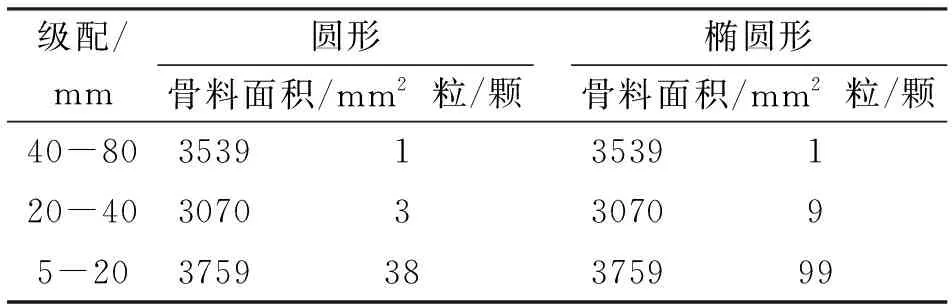
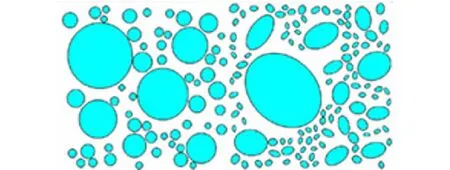
其中:PC为截面上任一点具有直径D 由各个级配的面积占比可计算得出各个级配对应的骨料个数[6]为 Ni=int(A·P0/Ai) (2) 其中:Ni为某粒径区间内的骨料个数,A为试件截面的总面积,P0为粒径范围区间为[Di,Di+1]的骨料出现的概率,Ai为某粒径区间内骨料截面的有效面积。 由于研究方法的不同, 随机骨料模型的骨料投放量的判别方法分为了骨料面积判别和骨料颗粒数判别两种, 如吕钊[6]以骨料面积占比为依据控制骨料投放的量, 而王彩峰[7]则通过公式(2)计算得出各个级配骨料个数来进行骨料的投放。 本文分别编制了两种不同判别方法的投放与生成程序, 以下详细说明各个骨料生成与投放程序的算法。 由蒙特卡洛法定义圆心坐标(x,y)及圆形半径r为随机变量来表征圆形骨料的随机性, 具体投放步骤如下: 1)设置骨料投放的区域, 将试件截面的宽和高分别设置为Width,Height, 由式(1)、 (2)可按研究需要计算出各个级配的所占面积或骨料颗粒个数。 考虑到各个级配的界面层厚度不同, 且骨料影响范围系数的值存在不确定性, 本文对各个级配的界面层厚度分别进行设置。 2)随机生成圆形骨料的圆心坐标并判断该圆形骨料是否在投放区域内。 将每一个骨料的坐标参数进行判断, 各个骨料参数需满足坐标与半径之差大于零, 与半径之和小于宽度和高度。 如不满足判定条件则重新随机生成对应参数, 如满足则继续运行。 3)判断各个圆形骨料之间是否有重叠部分。 可利用循环遍历的功能将每个新生成骨料和之前生成的所有骨料作对比, 如两圆相离则继续运行, 如两圆相交或相切则返回步骤2)中重新随机生成对应参数。 4)判断生成的骨料是否已满足生成要求。 如采用颗粒数判断, 则由公式(2)计算得出各个级配的骨料数目, 在判定生成的骨料总数及各个骨料级配数目是否满足要求, 如采用面积判断, 则判断生成骨料总面积占比是否满足要求, 如满足则继续均匀性判断, 如不满足则返回步骤(2)重新生成对应参数。 5)输出各项参数绘制图形。 为表征椭圆骨料形状和位置的随机性, 将其形心坐标(x,y), 长轴长度(a), 短长轴之比(c)以及旋转角度(cita)定义为随机参数, 具体投放过程如下: 1)设置椭圆形骨料的投放区域。 设置截面宽高长度, 考虑到椭圆形骨料形状不宜过于扁平, 为避免畸形骨料的产生, 椭圆短长轴之比的随机区间设置为(0.5, 0.8), 由于椭圆的对称性, 其旋转角度区间可设置为(0, 180)。 2)按照步骤1)中的随机区间生成形心坐标(x,y), 长轴长度(a), 短长轴之比(c)以及旋转角度(cita)五个随机参数。 3)判断生成的椭圆是否在投放区域内。 平面内椭圆可以简化为一般方程, 即: ((x-m)cosθ+(y-n)sinθ)2/a2+ 由此可以将问题转化为判断椭圆方程和边界线段方程联立是否有实数解, 如无实数解则生成的椭圆均在投放区域内, 反之则返回步骤2)重新生成椭圆方程。 方程求解可运用Python中的solve模块, 但是考虑到solve模块运行速度不佳, 为避免运算时间较长, 可在求解前进行筛选, 采用与圆形骨料类似的方式, 判断以a×c为半径的圆形骨料是否在投放区域内, 如在投放区域内, 再通过solve去求解, 由此可以过滤掉部分不满足的骨料, 提高计算效率。 4)判断各个椭圆之间是否有重叠部分。 对于两个椭圆的位置关系的判定方法有多种, 如椭圆内接多边形法, 椭圆外接多边形法等, 这些方法是通过对比多边形顶点和椭圆焦点的距离和来判断两椭圆位置关系, 然而精确度并不高。 目前最准确最常用的判断方法是由刘洋[8]提出的广义特征多项式法, 通过比较广义特征多项式的根的符号判断椭圆的位置关系。 但是求取特征多项式的过程中涉及到多次矩阵运算, 且运算时间较长, 运算精度不易控制。 因此本文并未采用该方法判断两个椭圆的位置关系。 考虑到椭圆可由圆沿某一个方向按照某一个比例压缩得到, 本文采用椭圆外接圆的方法, 以椭圆长轴长度为半径, 形心为圆心做圆, 通过上述圆形骨料的位置关系判别方法判断, 虽然投放最大效率有所降低, 但运算时间也相应减少, 且基本符合投放需求。 将新生成椭圆参数与之前所有已生成的椭圆参数做判断, 若该椭圆参数满足判定条件则向下运行否则返回步骤2)重新随机生成五个随机参数。 5)判断投放量是否满足要求, 判断方法同圆形投放相同, 如满足则进行均匀性判断, 如不满足则返回步骤2)重新生成各项参数。 6)输出椭圆形各项参数绘制图形。 目前随机骨料的投放程序缺乏对骨料均匀性的判定, 本文将投放区域划分为上中下三个区域, 分别计算各个区域内投放骨料的面积占总投放骨料面积的比值, 若比值范围均为30%~36%, 即认为骨料投放较为均匀。 并基于Python语言编制对应的二维圆形, 椭圆形的随机骨料模型投放程序及其面积计算程序, 使程序产生的骨料既表征其位置和形状大小的随机性也保持了混凝土中骨料的均匀性。 如选择截面为150 mm×150 mm的混凝土试件, 将其划分为等距的上中下三个投放区域, 每个区域截面为150 mm×50 mm。 向其中投放三级配骨料, 骨料投放区间分别为(40,80)mm;(20,40)mm;(5,20)mm。 分别计算三个投放区域内已投放完成的骨料的面积与投放骨料总面积之比, 若三个区域的比值均在30%~36%之间则判定为均匀性较好。 考虑到骨料不仅单独存在于某一个区域还有跨越多个区域的情况, 需分类讨论, 具体步骤如下: 1)按照骨料形心的纵坐标将骨料圆心位置划分为处于上、 中、 下区域三类。 2)将各类骨料按照跨越区域情况再进行分类讨论, 如骨料圆心处于上区域, 则可分为骨料全部处于上区域或者骨料跨越上中两区域, 同理, 骨料圆心处于下区域可分为全部处于下区域或跨越中下两区域, 考虑到时骨料粒径最大为80 mm而每个区域高度为50 mm, 所以只有圆心处于中区域的骨料才可能同时跨越上、 中、 下三个区域, 因此将圆心处于中区域的骨料分为全部处于中区域、 跨越上中区域、 跨越中下区域以及跨越上、 中、 下区域四种情况。 3)按照不同情况进行求解。 当骨料仅处于某一个区域时, 根据圆形面积公式求出该骨料面积即可, 当骨料跨越两个区域时, 如图1所示, 骨料在中区域的面积为扇形OAB减去三角形OAB的面积, 角AOB可由OA和OD的长度由反三角函数求得, 由此易得扇形OAB面积, 进而求出骨料在中区域的面积, 骨料于上区域的面积为该骨料面积减去在中区域的面积。 当骨料跨越三个区域时, 同理通过扇形OAB减去三角形OAB的面积求出该骨料在上区域的面积, 通过扇形OCD减去三角形OCD的面积求出该骨料在下区域的面积, 用该骨料总面积减去上、 下区域的面积即求得中区域的骨料面积。 图 1 圆形骨料分布情况示意图 4)遍历所有生成的骨料, 按照上述方法分别计算得出上、 中、 下三个区域内的骨料面积, 与骨料投放的面积做商, 求得各个区域内的面积占比。 若面积占比在30%~36%之间, 则判定其投放较为均匀。 均匀性判断的流程如图2所示。 图 2 均匀性判定流程图 同圆形骨料相同, 选择截面为150 mm×150 mm的试件为例, 三级配骨料, 具体求解方法如下: 1)按照骨料形心的纵坐标将骨料圆心位置划分为处于上、 中、 下区域三类。 2)根据骨料跨越区域情况分类讨论, 与圆形骨料不同:椭圆形骨料不能仅凭形心和半径的关系来判断是否有跨越区域的情况, 本文选择将椭圆转化为一般方程, 通过与y=100和y=50两个分界线求解, 若存在实数解即存在跨越区域情况, 若不存在实数解说明该骨料仅存在于形心所在区域。 3)根据不同情况分别计算骨料在各个区域的面积。 当骨料跨越两个区域时(图3), 考虑到目前针对于部分椭圆面积的求解上没有一个特定的公式, 本文采用微积分思想, 用椭圆一般方程和y=100求解, 得出的两个实数解即为A、 B的横坐标, 将A、 B之间划分为20段, 将部分椭圆面积转化为20个直角梯形面积之和。 由此可以求出椭圆在上区域的面积, 通过椭圆面积减去在上区域的面积即可求得其在中区域的面积。 当骨料跨越三个区域时(图3), 同理采用上述方法求得骨料在上、 下区域内的面积, 再通过骨料面积减去上、 下区域的面积求得骨料在中区域的面积。 图 3 椭圆形骨料分布示意图 4)遍历所有的椭圆形骨料, 计算三个区域的骨料面积, 判定其是否投放均匀。 以在截面尺寸为150 mm×150 mm的混凝土试件中投放三级配骨料为例, 骨料级配区间分别为(40,80)mm;(20,40)mm;(5,20)mm, 其界面层厚度分别设置为0.5 mm, 0.4 mm, 0.3 mm, 假设投放面积百分比为62.8%, 通过式(1)、 (2)计算得出各个骨料级配的颗粒数目, 计算结果如表1所示, 生成模型如图4所示;同理, 选择同样级配的骨料采用面积法投放, 计算结果如表2所示, 生成模型如图5所示;对照表1表2可以看出两种判别方式的投放程序均能完成骨料投放过程, 但椭圆形颗粒数判断方法投放模型的各个级配的骨料面积均比预定面积较低, 可适当调整各级配椭圆形骨料的有效面积, 在根据式(2)算出更为准确的骨料颗粒数。 表1 颗粒数判断方法计算结果 图 4 颗粒数判断方法生成模型 表2 面积占比判断方法计算结果 仍选择试件截面为150 mm×150 mm, 三级配骨料, 骨料级配区间分别为(40,80)mm;(20,40)mm;(5,20)mm, 其界面层厚度分别设置为0.5 mm, 0.4 mm, 0.3 mm, 各级配投放面积占比按表2所述, 本文随机生成20组未经过均匀性筛选的骨料模型数据, 分别计算其三个区域内的骨料面积占比, 其中达到均匀性判定要求的圆形骨料仅有4组, 达到均匀性判定要求的椭圆形骨料仅有6组, 综合来看符合均匀性要求的仅占25%, 将各个区域骨料面积的离散程度用方差表示, 其均值选择为33.33%, 部分未筛选骨料各区域占比面积方差高达0.069, 圆形骨料平均方差为0.0297, 椭圆形骨料平均方差为0.019, 然而进行均匀性筛选后的骨料各个区域的面积占比方差几乎不会超过0.01。 由此可见随机生成骨料的均匀性不高, 各区域骨料面积离散程度较高, 因此进行筛选是非常有必要的。 本文从20组数据中选取其中较为典型的两组如表3所示, 使用该数据生成对应的骨料模型。 其中, 不进行均匀性判断所生成的骨料模型如图5所示, 通过均匀性筛选之后的骨料模型如图6所示。 由表3可以看出未经过均匀性筛选的骨料投放到各个区域的面积占比方差较大, 离散性较高, 所以其均匀性较差, 而筛选完成后各个区域骨料分布较为合理, 各区域面积占比方差不大于0.01, 所生成的随机骨料既满足位置和形状的随机性, 也可以满足骨料分布的均匀性。 图 5 面积占比判断方法生成模型 图 6 均匀性筛选的骨料模型 表3 筛选前后各区域骨料面积占比 1)根据不同的研究需求, 将随机骨料投放量的限定条件分为骨料颗粒数判断和骨料面积占比两种, 并编制不同形状、 不同级配的随机骨料投放程序。 以三级配混凝土为例, 颗粒数判断和面积判断方法完成的骨料投放均可满足投放需求。 2)在原来随机骨料生成的基础上, 通过区域面积占比对其骨料均匀性进行判定, 并编制对应的程序, 使投放的骨料既满足其位置和形状的随机性也满足其分布的均匀性。1.2 二维圆形随机骨料的生成算法
1.3 二维椭圆形随机骨料生成算法
((m-x)sinθ+(y-n)cosθ)2/b2=12 骨料均匀性判别方法
2.1 圆形骨料均匀性判别方法
2.2 椭圆形骨料均匀性判别方法
3 骨料投放及均匀性判别实例
3.1 两种判断方法生成骨料实例
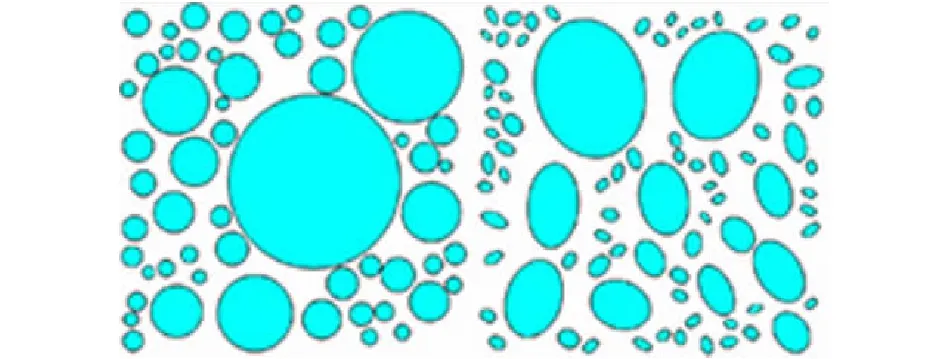
3.2 加入骨料均匀性判断前后对比
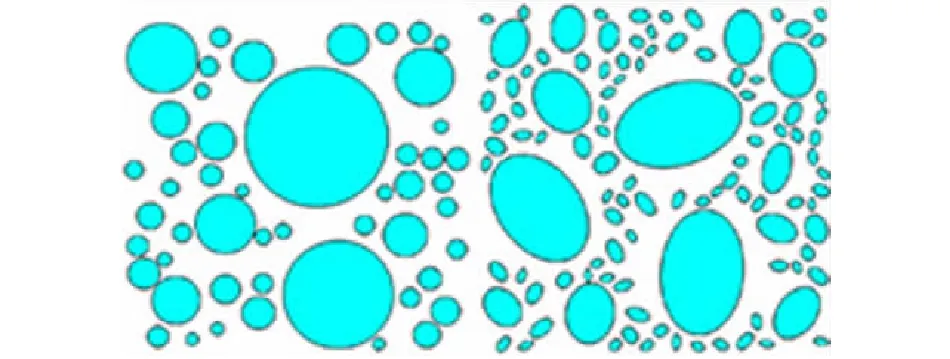

4 结论

