基于SAP2000的框剪结构抗连续倒塌研究

柯长仁， 姚东浩

(湖北工业大学土木建筑与环境学院， 湖北 武汉 430068)

建筑结构的连续倒塌问题逐渐成为近些年来结构安全研究的重点部分。自1968年发生于英国的Ronan Point公寓的煤气爆炸引起的连续倒塌事件后， 各国开始重视结构的连续倒塌问题， 并因此制定了相应的设计规范和指南。而在经历发生于美国1995年Alfred P. Murrah联邦政府办公楼和2001年“911”事件纽约世贸大厦等多起严重连续倒塌事件后， 结构的抗连续倒塌设计越发受到工程界的重视， 我国学者也开始将目光转向其中， 成为21世纪以来结构安全问题的研究热点[1]。相应的， 相关设计规范也进行了改进[2]， 2020年9月26日， 世界上最大的抗连续倒塌实验更是在我国徐州顺利完成。但是当前的研究对高层结构而言可能不太适用， 因为当前国内外大量研究大多以多层框架为主。黄华， 刘伯权等[3]使用SAP2000软件对钢筋混凝土框架进行了连续倒塌分析， 针对钢筋混凝土框架剪力墙结构， SAP2000软件在其分析的运用较少。陆新征， 任沛琪等[4]在对框架剪力墙结构进行连续倒塌分析时发现：如果结构中部位置布置剪力墙， 且所布置的剪力墙相互连接贯通形成筒状结构， 在部分剪力墙失效拆除后剩余剪力墙仍具有较强的抗连续倒塌能力。而在角部位置布置L型剪力墙， 若剪力墙部分失效， 结构连续倒塌效率如何变化尚未可知。本文根据中国《混凝土结构设计规范》(GB50010—2010)设计一栋典型24层钢筋混凝土(RC)框剪结构， 建立其有限元模型， 利用SAP2000中的非线性动力方法对结构进行拆除构件分析以验算其连续倒塌能力。研究剪力墙为L型并位于角柱附近时， 分别拆除各个类型柱子， 结构的连续倒塌概率如何变化， 拆除剪力墙时， 结构的连续倒塌能力如何， 拆除不同位置剪力墙时， 结构的连续倒塌能力如何。

1 钢筋混凝土框架-剪力墙模型

1.1 模型设计

根据我国现行的《混凝土结构设计规范》[5]和《建筑抗震设计规范》， 运用PKPM设计软件来设计框剪结构计算模型。 以某二十四层框剪结构为例(图1, 图2), 结构层高一至四层分别为6 m、5 m、 5 m和2.2 m,五至二十四层层高均为3.15 m， 总高度81.2 m， 地处7度抗震设防区域。场地为Ⅱ类， 地震分组第一组， 基本风压为0.45 kN/m2， 剪力墙与框架抗震等级均为二级。屋面恒载5.5 kN/ m2， 活载2.0 kN / m2， 一至三层恒载5.0 kN/m2， 活载3.5 kN/ m2， 四层恒载3.9 kN / m2， 活载2.5 kN/ m2， 五至二十四层恒载5.5 kN/ m2， 活载2.0 kN/ m2。四周外围墙：二至三层13.5 kN/ m2， 四至二十四层8.0 kN/ m2。混凝土强度等级及钢筋牌号如表1所示。模型构件尺寸见文献[6]。

图 1 框架-剪力墙结构三维结构图

图 2 结构平面布置图及构件初始破坏位置

表1 混凝土强度等级及钢筋牌号

1.2 分析平台及计算模型

由于对结构的构件进行连续倒塌设计属于整体力学行为，运用实验进行研究不太符合实际，因此我们在实际工作中主要运用有限元分析进行研究。在本次研究中使用由美国CSI公司开发研制，迄今为止已有四十多年历史的商业有限元软件SAP2000[7]；该软件具有强大的计算分析功能，并且计算快速、合理，本次研究中我们仅使用其非线性动力分析功能。本文中的框架梁及柱采用线单元，剪力墙采用分层壳单元。为简化分析，有限元模型中未建立楼板的模型，但是将楼板自重及楼板的荷载等效到相应的支撑梁上，在不考虑楼板的前提下，计算结果偏于安全。

1.3 破坏准则

分析中采用GSA2003[8]规定的荷载组合，即在进行动力分析时，使用式 L=DL+0.25LL。GSA2003中规定非线性分析时采用塑性铰转动和位移延性比来衡量，其判定准则为转角大于6°时认为结构会发生连续倒塌。

1.4 分析方法

在本次研究中为了从整体评价结构的抗连续倒塌能力采用非线性动力拆除构件法对结构进行分析，这是目前可知分析方法中较为准确、使用较为广泛的方法[9]。该方法在考虑结构几何非线性与材料非线性的前提下也反映结构的动力响应、P-Δ效应。所以运用此方法来进行分析，不仅可以适用多种结构，更可以使分析数据更加精确。

采用PKPM计算得到结构内力和配筋，将其模型导入SAP2000中，通过非线性动力分析拆除构件法分析框架的抗连续倒塌性能。非线性动力拆除构件分析的基本流程按照DOD2010[10]的规定首先让结构在重力荷载作用下达到静力平衡状态; 然后，在较短时间内迅速拆除目标构件(在有限元模型中瞬间杀死相应单元) ；最后，对结构进行非线性动力分析得出失效点的位移及塑性转角。本文分别采用拆除底层和十层角柱、长边中柱、短边中柱、中心柱以及剪力墙为十种不同的连续倒塌分析工况，每次分析只拆除一种代表构件。

2 框架部分柱失效分析

2.1 拆除不同楼层同一位置构件

塑性转角均小于规范GSA的限值6°，结构没有发生连续倒塌破坏(表2)。

图3a、图3b所示为首层长边中柱拆除前后结构整体变化情况，图3c、图3d为十层长边中柱拆除前后结构整体变化情况。可以看出结构长边中柱拆除后，结构的变形明显，而且十层长边中柱拆除后结构变形大于首层拆除长边中柱后结构变形。

塑性转角均小于规范GSA的限值6°，结构没有发生连续倒塌破坏(表3)。

表3 拆除角柱

塑性转角均小于规范GSA的限值6°，结构没有发生连续倒塌破坏(表4)。

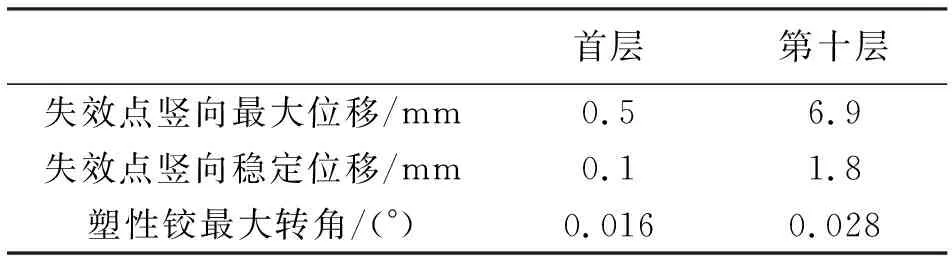
表4 拆除短边中柱

塑性转角均小于规范GSA的限值6°，结构没有发生连续倒塌破坏(表5)。

表5 拆除中心柱

由以上分析可知，在角柱与短边中柱附近设置剪力墙可在该柱失效后明显降低该柱节点的竖向位移，改善其抗倒塌性能。在拆除本结构任一楼层相同位置典型柱子时，结构均不发生连续倒塌。对于同一建筑同一位置，失效构件所处的层数不同，导致结构连续倒塌的敏感性也不同。以长边中柱为例，十层失效点竖向最大位移78 mm大于首层失效点最大位移53 mm,竖向稳定位移十层52.8 mm大于首层33.7 mm,塑性铰最大转角十层0.074°大于首层 0.057°。同样的，拆除不同楼层其他同一位置构件，随着构件所处层数的增高，失效点竖向位移以及塑性铰转角相应变大。由此可判断楼层越高，拆除同一位置构件的连续倒塌概率越大。这是因为底层结构相比于上部结构配筋率更大，使其极限承载能力高于上部结构，除此之外底层柱拆除后，其上部结构超静定次数相对上部构件失效较大，这些原因导致拆除底层柱后剩余结构仍有较大的冗余度。

2.2 拆除同一楼层不同位置构件(首层)

拆除不同位置柱失效点竖向位移时程曲线对比见图4，由于短边中柱竖向位移过小，故在此图上不多赘述(表6)。由表6可知：

1)首层无论拆除角柱，长边中柱，短边中柱还是中心柱，其塑性转角均小于6°，故根据规范结构不会发生抗连续倒塌破坏。

2)拆除同一楼层不同位置柱构件时失效点最大位移长边中柱为53 mm>中心柱40.6 mm>角柱1.5 mm>短边中柱0.5 mm，对于失效点稳定位移同样是长边中柱>中心柱>角柱>短边中柱,对于塑性铰转角而言，同样是长边中柱0.057°>中心柱0.01°>角柱0.003°>短边中柱0.0016°。根据GSA2003判定准则为转角大于6°时认为结构会发生连续倒塌由此得出拆除长边中柱后此结构发生连续倒塌的概率最大，中心柱次之，之后是角柱，短边中柱最小。

3)角柱失效后形成悬臂结构承受原结构上部的竖向荷载，理论上来说在上部竖向荷载作用下发生连续倒塌的概率要超过长边中柱和中间柱，但是由于本结构中角柱失效后与其相连的梁还受到L型剪力墙的约束，其约束力要远大于长边中柱和中间柱失效后周围柱对梁的约束，故角柱失效后结构抗倒塌能力仍然强于长边中柱和中间柱失效情况。

4)因其承担荷载小，短边中柱失效后产生的不平衡荷载也最小，而且在本结构上与其相连的梁同样受到L型剪力墙的约束。这两方面原因综合使短边中柱就算失效仍具有最强的结构抗倒塌能力。

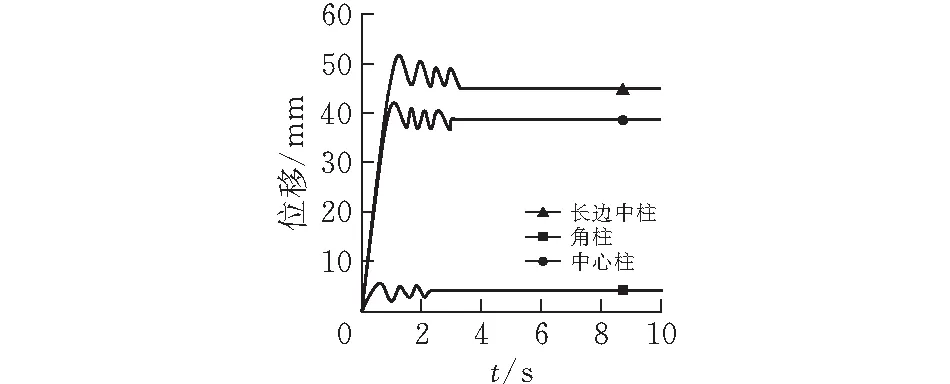
图 4 拆除不同位置柱失效点竖向位移时程曲线对比

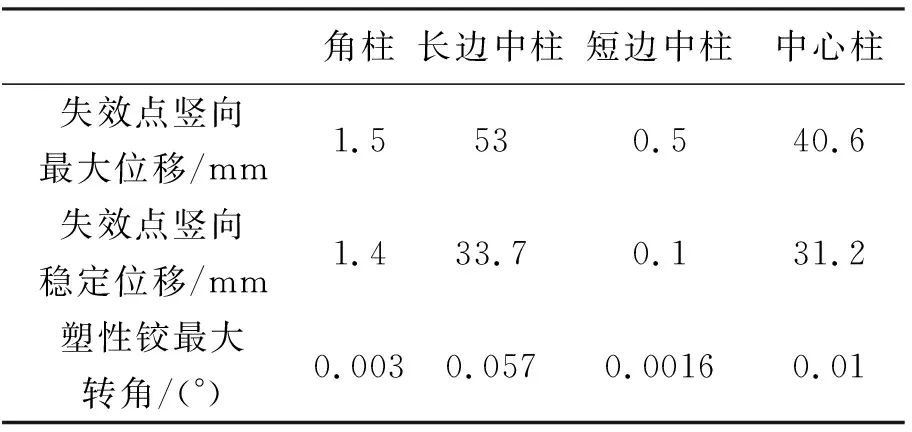
表6 拆除不同位置柱

3 剪力墙部分失效分析

3.1 拆除首层剪力墙Y向

剪力墙拆除位置如图5所示，位于角柱附近的L型剪力墙，图6所示为首层L型剪力墙失效后竖向结点位移变化曲线，图7为其失效后失效点竖向加速度变化曲线，失效后大约0.5 s时结点加速度达到最大的2.5 m·s-2，1.5 s之后加速度逐渐稳定为0.竖向位移达到最大值2.1 mm的时间发生在1.25 s时，从位移变化可以看出位移波动幅度较小，周期也相对较短且不规则，具有较快的衰减速度，其位移稳定在1.5 s时，数值为1.9 mm,这是因为我们将L型剪力墙的Y向拆除后，X向墙体与剩余结构仍然有很好的空间拉结作用，并与Y向失效后剩余墙体相互约束产生较好的抗结构倒塌能力。

图 5 被拆除剪力墙示意图

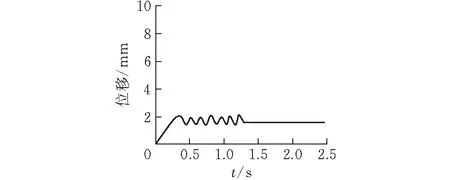
图 6 首层失效点竖向位移

图 7 首层失效点加速度

3.2 拆除首层与第十层同一位置剪力墙

表7所示分别为首层与十层L型剪力墙失效后结点竖向位移值和塑性铰最大转角，图8所示为不同楼层同一位置剪力墙失效后竖向结点位移变化曲线，图9为其失效后失效点竖向加速度变化曲线，由表7可以看到，十层的竖向节点最大位移为7 mm，竖向稳定位移为6.9 mm，明显大于首层的节点最大位移2.1 mm与稳定位移1.9 mm，塑性转角十层也明显大于首层，由图9可以看出竖向加速度明显高于首层节点位移和加速度，根据判断准则可以知道失效构件所在层数的高度与结构动力反映的剧烈程度成正比，楼层越高导致发生连续倒塌的概率越高。

表7 拆除不同楼层剪力墙

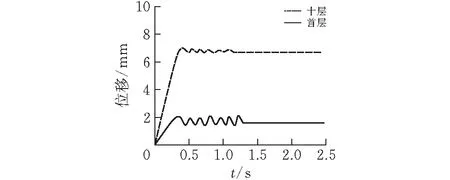
图 8 不同楼层失效点位移

图 9 不同楼层失效点加速度

4 结束语

通过建立一个24层典型框架-剪力墙结构模型，在SAP2000有限元软件中利用非线性拆除构件法研究其抗连续倒塌能力。分别拆除首层和十层角柱、长边中柱等典型柱构件以及剪力墙，分析这十种拆除工况的计算结果，得出了以下结论：

1)在角柱和短边中柱位置布置剪力墙，在该柱失效后可明显降低该柱节点的竖向位移从而增强其抗连续倒塌性能。

2)拆除不同楼层同一位置的柱子时，随着构件所处层数的增高，失效点竖向位移以及塑性铰转角也相应变大。主要是因为底层结构相比于上部结构配筋率更大，使其极限承载能力高于上部结构，其上部结构超静定次数相对上部构件失效较大，由此可知拆除底层柱后剩余结构仍有较大的冗余度。

3)在角柱和短边中柱布置剪力墙，拆除长边中柱后此结构发生连续倒塌的概率最大，中心柱次之，之后是角柱和短边中柱。

4)在结构角部布置相互连接的L型剪力墙，即使L型剪力墙一个方向的墙体被拆除，结构的抗连续倒塌能力也不会降低多少，这是因为在一个方向的墙体被拆除后，在其垂直方向的墙体仍然可以较好完成内力重分布，使剩余结构具有很好的空间拉结作用，除次之外，失效后剩余墙体与其垂直方向墙体还会相互约束，也会增强抗连续倒塌能力。失效剪力墙构件所在层数的高度与结构动力反映的剧烈程度成正比，楼层越高导致发生连续倒塌的概率越高。