空气润滑船底的试验研究
朱珉虎
(江苏省船舶设计研究所 镇江212003)
引 言
应用空气润滑原理来减少船之阻力,在高速船方面的进展较快。自20世纪60年代以来,各种表面效应船、气垫船纷纷问世,但在低速船方面的进展却很有限。由于在低速情况下,船底充气腔具有不稳定性。采用横隔条或横隔堵(横隔条是指其深度与纵向隔板或侧壁不齐平的横向挡板,主要起阻尼作用;横隔堵则是指其深度与纵向隔板或侧壁齐平的横向挡板,主要起分隔气室的作用。)虽有利于气腔的稳定性,但对阻力的影响却很少见诸于文献。
本文只讨论空气润滑船底在低速船上的应用,特别是在大尺度的内河平底驳船上应用空气润滑船底将获得较高的经济效益。一般是在船底的平坦部位设置一个矩形空腔,两侧为刚性侧壁,首尾设带线型的刚性槛板或柔性气封,里面充以空气。所以也可以看作一个水下充气腔或气泡。如果把这种气腔或气泡看成无限宽,忽略其边界影响,则可以用二维空泡流的理论来论述其稳定性问题。
1 二维充气腔的稳定性问题
假设在自由液面下一定深度h
处存在一个无穷水平面。假定来流方向为水平,且是均匀流。如果在垂直来流方向设置一带线型的槛板,并假定此槛板的横向宽度无限(如图1所示),则来流通过槛板后,流线将发生分离(离开水平面),形成一个空泡。这种空泡形成的机理同带横隔堵的空气润滑船底的空泡形成机理类似。如果流速相当高,流束内压力降低,以致在常温下产生水蒸汽,加上从水中析出的空气,便有可能在槛板后面形成一个空泡,如同在水翼翼背和螺旋桨叶片背面见到的空泡一样。但在低速空气润滑船的情况下,如果不在槛板后面充气,则空泡的边界是不稳定的,就会形成旋涡。
来流空泡数:

σ
为来流空泡数;p
为非骚动流中的静压力,Pa;ρ
为液体密度,kg/m;v
为非骚动流中的速度,m/s;p
为空泡中压力,Pa。实际上只有在p
接近于p
时才会形成空泡。一般说来,尾部的槛板实际上是不存在的,而且尾部的流动情况往往是不稳定的,只能“虚拟”地模拟一种贴合状态。为了便于研究,通常假定液体是理想的(即没有黏性),流动是无旋涡而稳定的,则此时流动中任意点的压力可按柏努利方程来确定:
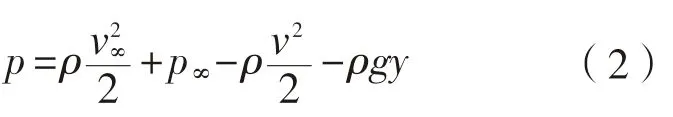
p
为流束中任意点的压力,Pa;v
为该点的流动速度,m/s;y
为该点的纵坐标(注意:向下为正),m;g
为重力加速度,m/s。由于沿界流在越过空泡区段内的压力是连续变化的,在自由边界上它等于p
,令式(2)右边部分等于p
,经过式(1)代入变换后得:

Fr
为参数,主要是考虑重力的作用。式(3)的物理意义是空泡边界的形状与空泡数和速度增量之间存在着函数关系,并且要考虑重力的作用。
空泡边界上的速度v
与槛板的形状和空泡边界的形状有联系,若能找到这一联系并代入式(3),那么可以得到一个关系式,从而在给定σ
值时能确定空泡边界的纵坐标y
。实用意义是建立薄的气层,即气室的最大厚度对长度之比很小,则按绕薄体流理论,v
的值与v
值相差很小,令速度的增量为u
,即
u
/v
的平方项,得到一个线性关系式:
式(5)给出了空泡边界形状的数学模式,为理论求解创造了条件。但对此式的求解有一定难度,故一般都是通过试验方法来获得空泡边界的形状及探索其稳定性问题。

图1 底平面下的绕流
注意到导出这个公式的前提是p
=p
,由于槛板的作用,u
> 0,故p
<p
时可建立稳定的气泡,而气泡的长度l
随v
和p
的增加而增加,当p
=p
时达到稳定的极限值。如果p
继续增加,则σ
出现负值,此时气泡的尾部出现不稳定的气水双相流。这在补充过大的空气量情况下时常出现的现象。如果气体速率相对于液体达到临界速率,则发生凯尔文-海尔姆霍尔兹不稳态。在不受边界限制的情况下,对空气和水而言,理论上的临界速度为6.6 m/s,但试验观察到的最小临界速度则要小得多,约为1 m/s。当有横隔条存在时,空气的流动受到阻尼,则可以推迟不稳态的出现。根据布图佐夫的论文,在水平边界的情况下,二维充气腔存在的条件为:

则充气腔的长度

l
< 4.9 m。因此,对于低速船来说,纵通的气室并不稳定,界面波的形成将大大降低空气润滑减阻的效果。同样,厚的气层虽然能防止界面波舔湿气室顶板,但空气的扰动不可避免,势必加速界面波形成而影响减阻效果。试验的结果也证实了这一点。2 两种新型气室结构及其试验方法
在内河平底驳船上,从实用观点出发,最好是建立一个薄层气室,这样可以利用原有驳船的双层底空间来改造。根据二维空泡流稳定性的理论,我们设计了两种截然不同的新型气室结构,见图2。
第1种气室结构如图2(a)所示。中间设置1道纵向隔堵,形成2个通长的气室,充气孔设在两端。在1个通长的气室中采用许多横隔条来产生空气阻尼,这些横隔条的高度较低,犹如1艘具有双层底的驳船拆掉外底板,只剩下内底板上的骨架。
第2种气室结构如图2(b)所示。它利用深度与侧壁齐平的横隔堵,将1个通长的气室分隔成几个等长度的小气室。这些横隔墙做成向后倾斜的斜坡状,充气孔设置在每个斜坡隔堵的上方。
两种气室的平面尺度相同,均为1.58 m×0.45 m。为测试空气润滑船底的减阻效果,以1艘同类型的驳船船模作对比试验。两个船模的尺度参见下页表1。
这两种气室都是耗气型的,需要不断地补充空气才能维持充气腔的存在。按照文献[1]得出的结论,空气由船尾逸出,可产生双相流推进作用,因此综合利用空气润滑和双相流推进作用会带来较好的节能效果,即充气所消耗的能量可从双相流推进中回收一部分。在设计良好的低速船上,双相流推进的效率甚至可与拙劣螺旋桨相当。

图2 两种气室结构

表1 常规驳与空气润滑驳船模的主尺度
船模试验的方法是采用常规试验。为了弄清楚空气润滑船底的减阻效果,我们把船体的形状设计成西漳驳形式(西漳驳是江苏内河广泛使用的拖驳船队最常见的驳船形式,因来源于无锡西漳村而得名),这样我们可与1艘常规的西漳驳船模进行对比试验。尽管空气润滑驳的船模为了更有效利用船底面积,不得不对船底气室周围的线型稍微作些修改,但从表1的对比中可以看到两个船模的差别并不大。
船模试验委托交通部上海船舶运输科学研究所进行。该所拥有浅水试验池且从事过类似试验,在空气润滑船艇试验方面富有经验。空气润滑驳在试验时增加了充气用的鼓风机,它由1台家用吸尘器改制而成,风机的风量通过电压调节来实现。
在试验方法上也作了一些创新,即将空气润滑船模的气室做成活动式顶板,既可以变更气室的高度以搜索最适合的高度,也可同时更换气室的结构进行多方案试验。图3为试验用的船模,船底已经改换成第2种气室结构。

图3 试验用船模(第2种气室结构)
3 实验结果
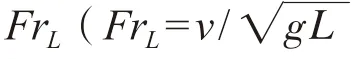
对于减阻效果,我们只能给出直观的船模阻力对比,由于目前对空气润滑船来说,尚无合适的船模-实船阻力的换算方法。因此,我们不讨论实船的减阻效果,只讨论气室各要素对阻力的影响。

图4 深水阻力曲线
我们对第1种方案做了变更气室高度的试验,所以在图4中画出3条阻力曲线,其对应的气室高度d
分别为5 cm、3.75 cm和2.5 cm。实验表明:d
= 3.75 cm时,第1种气室方案具有最佳的阻力性能。两种气室方案的浅水阻力性能在图5中给出。第1种气室方案中我们选用了最佳气室高度d
= 3.75 cm做浅水试验。第2种气室方案只有1种高度,所以浅水试验时气室高度仍为d
= 2.5 cm。显然第2种气室方案的浅水阻力性能较优(图中红线)。图5中的虚线是拆掉了第1种方案中的横隔条后做的,其试验条件完全与带横隔条时相同(即图中实线的试验工况)。实验结果表明:在低速段,横隔条是起减阻作用的;而到了高速段,情况则完全相反,横隔条反而使阻力有所增加,但这已经超出了这种驳船的常用航速范围。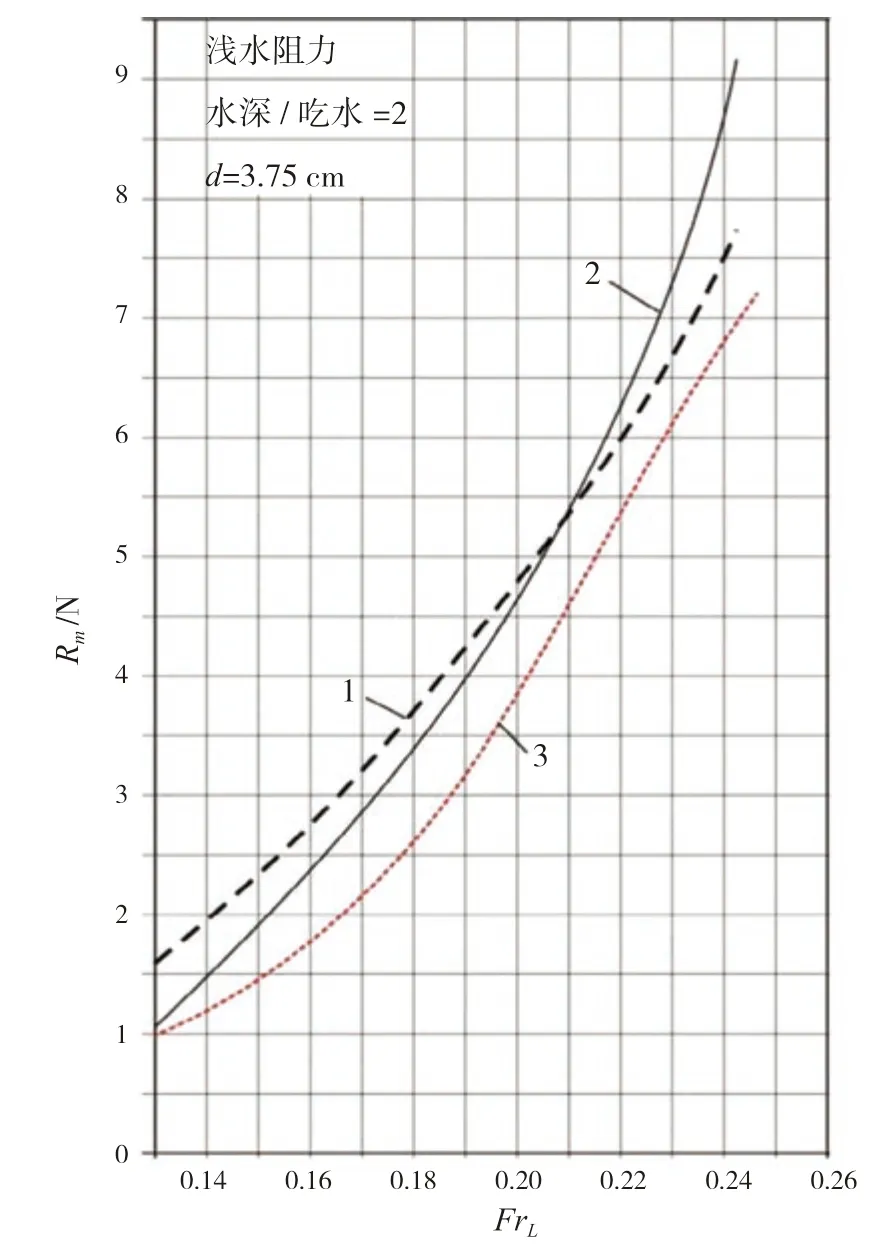
图5 浅水阻力曲线
关于气流量对阻力的影响在图6中给出。这是第1种气室方案在最佳高度时改变气流量参数得出的。

图6 气流量对阻力的影响
4 讨 论
4.1 气室高度对阻力的影响
该问题在国内外的文献中较少提及,并且有观点认为气室高度高则有利于改善阻力性能。然而,我们的试验却出现一个饶有兴趣的现象。当送风量不变,将气室高度从5 cm降低到3.75 cm时,阻力性能却有了大幅度改善,而且测得的阻力值非常稳定。当气室高度进一步降低到2.5 cm时,阻力性能骤然变坏。这说明对第1种气室构造来说,气室高度d
存在着一个最佳值,并非越高越好。这个现象并非偶然,当我们降低送风量之后再试,同样证实d
= 3.75 cm时的阻力性能优于d
= 5 cm时。正如理论推导中指出的那样,过量的空气运动会破坏充气腔的稳定性,导致减阻的效率下降。从理论上分析,气室的最佳高度应当与重力波有关,它取决于气室距水面的距离h
、船与水的相对速度以及气室的长度。根据试验所获得的数据,推荐在内河低速船上,第1种气室的最佳高度d
可取0.3 m左右,降低气室高度还有利于增加舱容和提高船身的利用率。第2种气室结构也进行了变高度试验,但它对高度变化的敏感性要低得多,说明由于气室长度分隔得较短,充气腔的稳定性进一步提高了。因此采用这种气室结构有可能进一步降低气室的高度。由图4可见,第2种气室结构在d
= 2.5 cm时的阻力性能甚至比第1种气室结构方案在d
= 5 cm时的阻力性能还要好一些,而高度仅为其一半。尤其是在浅水中,第2种气室结构的阻力性能优于第1种气室结构(见图5)。4.2 傅氏数FrL的影响
空气润滑船的阻力曲线有一些特征,首先它不像常规驳船的阻力曲线那样平滑上升,而是呈现一些波形曲率变化。大体上可以分为3段:
(1)低速段
此阶段阻力下降很快。除了空气润滑带来的阻力下降外,双相推进的作用很明显,它与送气量的大小有关。当送气量足够大时,低速段的阻力测不出来,即达到了双相推进作用的自航点。
(2)中速段
此阶段阻力曲线基本上与常规驳平行,但比常规驳船的阻力低,反映空气润滑减阻起主宰作用。
(3)高速段
此阶段阻力曲线呈陡峭上升,说明气室内出现骚动导致空气润滑减阻效果降低。
两种气室的3条阻力曲线几乎同时与常规驳船的阻力曲线相交,说明存在一个临界值,超过这个值之后,空气润滑船的阻力大于常规驳船。这一点在图4上对应的横坐标是Fr
= 0.285。由于我们用的船模尺度较小,Fr
就显得较高。如果放大船模尺度,在同样的拖速范围内试验,则Fr
相对下降,可以看到第2段的范围将会扩大,这是充气船底的主要工作段。因此,大尺度的平底驳船采用空气润滑的效果较好。前苏联曾对3 000吨级驳船进行过充气船底的模型试验,其阻力曲线的形状如图7所示。
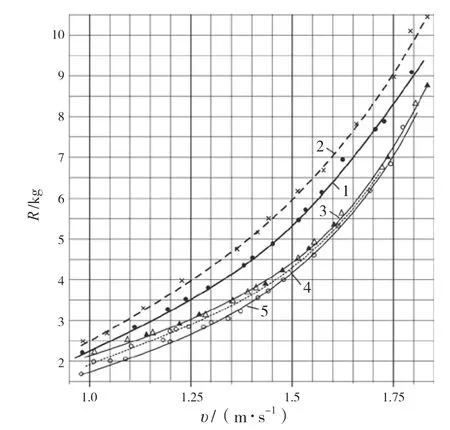
图7 吃水0.16 m时,3 000 dwt驳船模型的阻力曲线
图7中的虚线为常规驳船底的阻力曲线,3条细线代表空气润滑船底的阻力曲线,分别对应不同的充气流量。显然空气润滑减阻效果只是在中段最佳,两端都靠近常规驳船的阻力曲线。空气润滑减阻效果的最佳区段在船模速度1.25~1.80 m/s 之间,该船模气室长5.58 m,则Fr
在0.17~0.25之间。这个结论与图4得出的结论是相同的。由于我们使用的是西漳船型,文献[6]指出这种船型的最佳航速范围应限制在Fr
< 0.2的范围内,换算到空气润滑船底的情况,正好与Fr
= 0.25相吻合。临界值Fr
= 0.285是在深水情况下测得的,若在浅水情况下,则临界值要小得多。例如,当水深/吃水= 1.5时,测得的临界值为Fr
= 0.14。推究其原因,可用船底下绕流速度的增加来解释。4.3 充气量的影响
充气量的影响在图6中给出,这是第1种气室结构在最佳高度时测得的。对于一定尺度的气室来说,充气量也存在一个最佳值。充气量过小,则阻力性能迅速变坏;充气量过大,也只是在低速段引起双相推进作用的增加而减少阻力,且往往得不偿失,对于中速段阻力性能的改善很有限。而且过大的送风量往往会使阻力曲线变得陡峭起来,甚至破坏充气腔的稳定性,导致减阻效果下降。
由于我们使用的船模较小,充气量对阻力的敏感性要大一些,但对于一艘几千吨的大型驳船来说,充气量的变化对其阻力的影响可能极其有限。例如图7中的3条细线(曲线3~5)分别代表着3种不同的充气量。当充气量从0.39 L/s上升到4.45 L/s,即上升了11倍多,而阻力的变化只是在低速段较为明显,在高速段几乎趋于一致。
我们在试验中还发现:尽管所设计的两种气室结构并不相同,但最佳充气量则几乎一致,说明它不随气室结构的变化而变化。
4.4 横隔条的影响
通过两种不同气室结构方案的试验,我们对横隔条的影响有了进一步认识。以往的相关文献只是提到纵向和横向分隔有利于船的纵稳性和横稳性,因为空气润滑船发生纵倾和横倾时,空气会从一侧船底迅速逸出,使船产生负的复原力臂。增加纵向和横向分隔就好像减小自由液面的影响做法一样,甚至可能存在一种错觉,认为会对阻力性能不利。而本文的试验表明,横隔条或横隔堵对阻力性能的改善是有利的,这可以从图5 中清楚地看出。两条带有横向构件的阻力曲线(曲线2和曲线3)都比不带横隔条的阻力曲线(曲线1)更好。这虽是在浅水条件下获得的结果,但可按文献[6]提供的简易方法换算成深水情况,其结果将说明在最佳工作段内,横隔条的减阻作用毋庸置疑。横隔条的另一种影响是可以降低气室的高度,而这正是大部分内河驳船使用部门所期望的。
5 结 论
本文设计了两种空气润滑船底的气室结构,通过船模试验获得以下结论:
(1)第1种气室结构存在一个最佳高度,并非越高越好。根据试验所获数据,作者推荐在内河低速船上,第1种气室的最佳高度d
可取0.3 m左右。(2)第2种气室结构中的横隔堵提高了充气腔的稳定性。它不仅能够降低气室的高度,而且在浅水中的减阻效果更加理想。
(3)这种形式的空气润滑船底只适合在中、低速段运行。在高速段,阻力曲线呈陡峭上升,甚至超过常规驳船的阻力值,说明气室内出现骚动导致空气润滑减阻效果降低。试验表明傅氏数存在着一个临界值,超过这个值之后,空气润滑船的阻力将大于常规驳船,故建议空气润滑船底傅氏数使用范围为Fr
< 0.25。(4)充气量变化对阻力影响较小,但也存在一个最佳值,超过该最佳值会导致充气腔不稳定。
(5)横隔条或横隔堵对改善空气润滑船底阻力性能很有利。
21世纪是海洋的世纪,在以节能、减排、低碳为主调,倡导绿色航运和绿色船舶的时代,空气润滑减阻技术必将登上历史的舞台。

