Visual MODFLOW与GMS研究综述

李亚娇 张强 李家科 王毅凡

摘 要：为选择合适的地下水模拟软件，从而更好地解决实际地下水问题，从Visual MODFLOW和GMS的功能、数学模型、离散形式、剖分形式、建模方法、模拟精度方面对比分析，论述了MODFLOW模块改进以及Visual MODFLOW和GMS的应用进展。研究表明：相比Visual MODFLOW，GMS功能更加强大，在模型离散形式和网格剖分以及建模方法上具有一定优势;两者数学模型相同，边界条件设置各有利弊，模拟精度相当;Visual MODFLOW和GMS应用范围广泛，可为解决实际地下水问题提供参考，未来在模型功能、数据收集与处理、多领域交叉耦合模拟方面还有进一步发展空间。

关键词：地下水;数值模拟;Visual MODFLOW;GMS;有限差分

中图分类号：P641.8 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.04.016 引用格式：李亚娇，张强，李家科，等.Visual MODFLOW与GMS研究综述[J].人民黄河，2021，43（4）：89-93，130.

Abstract： In order to choose the appropriate groundwater simulation software， so as to better solve the actual groundwater issues， this article compared and analyzed the functions， mathematical model， discrete form， subdivision form， modeling method and simulation accuracy of Visual MODFLOW and GMS， and discussed the improvement of MODFLOW module and the application progress of Visual MODFLOW and GMS. The results show that， compared with Visual MODFLOW， GMS is more powerful， and it also has certain advantages in model discrete form， meshing and modeling methods; the mathematical models of the two are the same， the boundary condition settings have their own advantages and disadvantages， and the simulation accuracy is equivalent; Visual MODFLOW and GMS have a wide range of applications， which can provide guidance for solving actual groundwater issues. In the future， there is room for further development in model functions， data collection and processing， and multi-domain cross-coupling simulation.

Key words： groundwater; numerical simulation; Visual MODFLOW; GMS; finite difference

地下水具有穩定供水能力且水质优良，与人类生产生活密切相关，其重要性不言而喻。地下水研究方法经历了解析研究、物理模拟、数值模拟3个阶段。数值模拟主要借助计算机对建立的模型进行离散化求解。近30 a来，大区域地下水模拟理论[1]、地下水边界条件[2]、二维地下水时间步长研究[3]等一系列理论成果极大地促进了地下水数值模拟理论的发展。与此同时，地下水模拟软件不断涌现，这些软件功能强大，在处理地下水流、地下水溶质运移、淡-咸水界面迁移、地下水位变化等方面均有良好效果，随着软件的不断拓展开发、优化升级，其应用领域更加广泛，目前已涉及地下水资源评价、地下水资源开发规划、矿井水害防治、海水入侵、地下水优化管理等领域。国内外常用的地下水数值模拟软件有MODFLOW[4]、MT3DMS[5]、GMS[6]、Visual MODFLOW[7]和FEFLOW[8]等，其中Visual MODFLOW和GMS作为使用频次较高的两款软件受到广大研究者的关注，但对于两者未有细致的比较分析。笔者对Visual MODFLOW和GMS的功能、数学模型、离散形式、剖分形式、建模方法、计算精度等进行比较，综述二者多个领域的应用进展，据此提出现阶段的相关问题和将来的探索方向，以期为更好地解决实际地下水问题提供参考。

1 Visual MODFLOW与GMS概述

1.1 Visual MODFLOW概述

Visual MODFLOW是加拿大Waterloo水文地质公司在MODFLOW的基础上研发的一款致力于模拟评价地下水流动和溶质运移的三维可视化专业软件[9]。模型采用有限差分法模拟二维、三维饱和流状态下的稳定流与非稳定流、对流、弥散、化学反应以及粒子示踪，具有强大的可视化功能，能够实现用户与计算机的直接交流，操作界面简单，非常适合初学者。

1.2 Visual MODFLOW特点

①模拟步骤具有逻辑性、规范性;②在计算机上较为容易拟定模拟区域和剖分范围，可对剖分区域扩展或对网格多次精密细分;③含水层正交长方形网格剖分方便建立数据文件;④开采量变化时，软件会自动计算激发补给量;⑤能够实现含水层参数自动优化、补排边界性质自动判别;⑥兼容性强，适用范围广，求解过程简单，运算效率高;⑦能够接受GIS输出的文件，充分发挥信息处理和分析功能。

1.3 GMS概述

GMS（Groundwater Modeling System）是Brigham Young University环境模型实验室联合美国军队排水工作站研发的三维可视化地下水模拟软件。该软件采用模块化结构，综合了众多模型，比如MODFLOW、MODPATH、MT3D、FEMWATER等主要模块以及MAP、GIS、TINs等辅助模块[10]，功能十分强大，几乎涵盖了地下水的各个方面。该软件以有限差分和有限单元两种方法进行水流、溶质运移模拟，与其他同类软件相比，模拟范围更广，前后处理能力更强，界面更加友好。

1.4 GMS特点

①能够接受GIS输出的文件，充分发挥信息处理和分析功能;②模拟过程中大量使用节点、端点、线段、多边形等属性对象;③多种地下水建模方式;④模拟计算不仅仅是数值解，还有解析解;⑤具有PEST和UCODE两个自动调参计算模块，模型校正方便;⑥模块结构化设计易于扩展功能;⑦水文地质结构可视化效果明显。

2 Visual MODFLOW和GMS对比

2.1 软件功能

Visual MODFLOW由MODFLOW、MODPATH、MT3D、WinPEST、RT3D和Zone Budget组成，可进行二维与三维水流模拟、溶质运移模拟以及粒子示踪和水均衡计算，局限性在于不适宜模拟非饱和流、海水入侵等密度变化的水流和溶质运移[11]。GMS功能比较完善，除了Visual MODFLOW所具备的功能之外，还可通过FEMWATER来模拟非饱和流和密度变化的水流溶质运移，计算土坝防洪堤等剖面滲流量，模拟多相水流和运移，模拟地下水含水层空间分布转移概率，建立三维地层模型，管理钻孔数据和地质统计数据等，比Visual MODFLOW功能更加全面。

2.2 数学模型

Visual MODFLOW和GMS地下水流模型都以达西定律和质量守恒定律为基础，三维地下水流运动方程[12]为

式中：Kxx、Kyy、Kzz分别为沿x、y、z坐标轴方向上的渗透系数;h为测压管水头;w为在非平衡状态下通过均质、各向同性土壤介质单位体积的通量，即地下水的源和汇;Ss为孔隙介质的储水率;t为时间。

求解非稳定流问题时，还需要初始条件和边界条件。Visual MODFLOW采用模块化结构将边界条件进行分类，在实际模拟过程中可直接选择需要的边界进行编辑，十分便利，但在处理特殊的边界问题时需将几类边界联合使用来保证模拟的准确性。该软件无法设置第二类边界条件，通常的做法是利用抽（注）水井代替边界流量[13]。GMS边界条件是通过指针参数设定的，指针参数IBOUND=1表示流量边界，IBOUND=-1表示定水头边界，IBOUND=0表示隔水边界;另一种边界条件设定方法是选定具体单元，通过网格属性赋值实现。相比Visual MODFLOW，GMS边界条件设定相对灵活，但数据输入较为烦琐。

2.3 模型离散形式

Visual MODFLOW模型离散形式是有限差分。有限差分将定解问题中的偏导数以合适的数值微分公式换为差商，使得原问题离散化为差分形式，再进一步求出数值解。该方法物理概念明确，通俗易懂，且运算效率高，但在处理不规则边界问题时效果不佳。GMS模型离散形式是有限差分和有限单元。有限单元将计算域划分为有限个单元，在各单元内部借助变分法或加权余量法生成离散方程，再将各个离散方程组合成方程组进行离散求解。该方法对于非规则边界或物性参数复杂区域处理效果良好，但信息准备工作量大，解方程组困难[14];在处理非稳定流时，若时间步长较小，则易在源汇项附近出现水头反常现象[11]。

2.4 模型网格剖分形式

Visual MODFLOW以矩形对模拟区域进行剖分，这种方式方便数据文件准备，有利于输入文件的规范化，收敛速度较快。不足之处在于对一些重点地带加密时，会增加部分不必要的计算单元，而且刻画外部边界较为困难[13]。GMS采用有限差分和有限单元的离散形式，其网格剖分形式（矩形或三角形）较为灵活，在刻画外部边界时具有明显优势，网格加密只需对局部地带加密，对计算量影响较小[11]。

2.5 建模方法

Visual MODFLOW使用网格法建模，直接对剖分的网格进行源汇项和边界条件定义以及含水层参数赋值，适用于范围较小、水文地质条件较简单的区域。GMS建模方法除了网格法以外，还有概念模型法和Solid法。概念模型法通过对Coverage图层实体赋值调参来表示网格属性，工作量大大减少，适用于大范围的地下水建模。Solid法利用钻孔数据进行岩层界面标识，后续再进行插值生成Solids模型。该方法刻画地层空间结构效果逼真，适用于小范围且钻孔数据丰富的区域[15]。

2.6 模拟精度

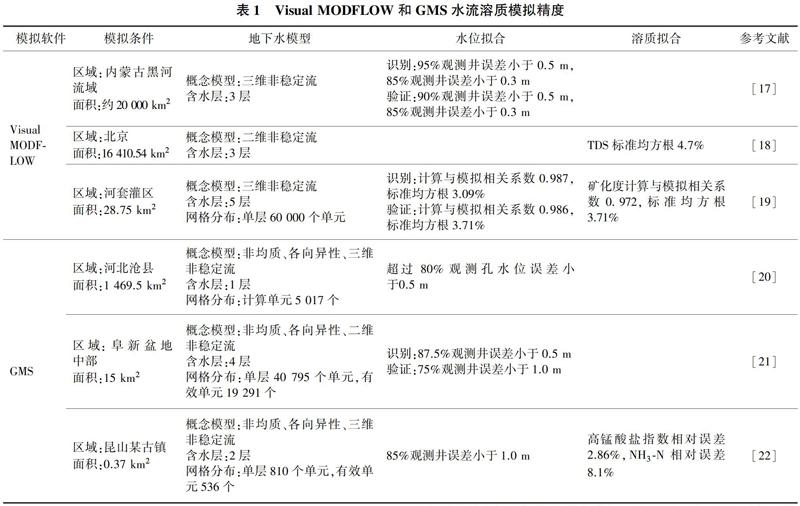
Visual MODFLOW和GMS广泛应用于地下水流和溶质运移模拟。表1总结了两款软件对水流模拟和溶质模拟的实际精度。两款软件在拟合较好情况下，水流模拟能够达到85%左右观测井水位拟合误差小于0.5 m，溶质浓度模拟能够达到均方根约4%的精度。地下水模拟误差来源主要为参数的不确定性、观测数据缺失、求解数学模型过程中的误差等[16]，实际工作中可通过强化物探技术、组合优化多种物探方法、实现数据资料云共享等方法来进一步提高模拟精度。

3 Visual MODFLOW与GMS的研究及应用进展

3.1 MODFLOW的改进应用

MODFLOW作为Visual MODFLOW和GMS的核心模块，其改进模型不断涌现。Mehl等[23]以MODFLOW为基础开发了局部网格加密技术，将模型分为大区域父模型和局部区域子模型，父模型和子模型通过不同的网格大小和数值计算方法进行模拟，能够有效减少运行时间并提高精度，局限性在于只能对规则区域的子模型进行加密嵌套。Krm等[24]介绍了MODFLOW新版本MODFLOW-USG，其支持各种结构化和非结构化网格类型，能够较好解决非连续性弱透（含）水层逐渐消失的问题。MODFLOW-CFP是一款较新的可以模拟地下水在管道（或洞穴）中的层流/非层流的数值模型，考虑了岩溶含水层参数（如弯曲度、壁面粗糙度、壁面渗透性等），较好体现非达西流特征[25]。Niswonger等[26]描述了MODFLOW-NWT处理非线性单元疏干再湿润的潜水层水流问题。Kim等[27]开发了SWAT的水文响应单元和MODFLOW的单元转换接口用于流量数据交换，用River程序包描述河流与含水层的相互作用，耦合模型SWAT-MODFLOW能够模拟地下水补给率、含水层蒸发量和地下水位的时空分布，较好表达饱和含水层和河道之间的关系。Morway等[28]将非饱和带水流程序包UZF1引入地下水溶质运移模型MT3DMS，能够准确模拟非饱和带的溶质运移、弥散和反应。MODFLOW各类拓展版本通常不兼容，Hughes等[29]描述了MODFLOW的新框架MODFLOW6，可支持多个不同类型模型，模型之间可交换信息并在矩阵水平上耦合。可以预见，MODFLOW6将成为处理复杂地下水问题的重要平台。

3.2 Visual MODFLOW和GMS的應用研究

（1）地质灾害预测。骆勇等[30]基于土力学经验公式、GMS的SUB模块、COMSOL Multiphysics模型，对比分析了由疏排水引起的地面沉降，结果表明GMS的SUB模块预测地面沉降具有一定的参考价值，但SUB模块没有考虑孔隙水压力的变化和土体沉降对渗流场的反馈影响，由此导致沉降量对水位变化响应过快。郑亚楠等[7]通过Visual MODLFLOW定量预测滑坡的稳定性，模拟结果表明，一般暴雨条件下（100 mm/d）滑坡体的后缘水位对滑坡体的稳定性起着重要作用。

（2）溶质运移模拟。曾伟等[31]以某制药厂为例，运用Visual MODFLOW模拟氯化物和甲醛在不同时间内的浓度及其所造成的影响，模拟结果表明，氯化物和甲醛分别在135 d和230 d时浓度严重超标，对潜水含水层造成巨大影响。高志鹏等[32]将“三氮”污染物通过包气带进入含水层最终稳定的浓度作为含水层的输入浓度，实现Hydrus-2D和GMS的耦合，在此基础上具体分析了“三氮”污染物在包气带和饱水带受土壤吸附、硝化作用、包气带厚度综合影响下的迁移转化规律。

（3）涌水量预测。宫厚健等[33]应用Visua1 MODFLOW对比分析了未受流场干扰和受到流场干扰两种情况下矿井采区涌水量，并对结果进行验证，结果表明考虑流场干扰的方法更加先进、准确。Golian等[34]利用GMS软件中的MODFLOW模块模拟预测隧道掘进机（TBM）推进过程中的涌水速率，该方法充分考虑了掘进过程隧道渗流条件、介质特性和水头的变化，可用于隧道施工过程地下水的瞬态模拟。

（4）设计方案优化管理。Liolios等[35]利用Visual MODFLOW研究了蒸散和降雨对水平潜流人工湿地出水浓度的影响，同时引入衰减系数研究了蒸散和植被、温度、介质尺寸、水力停留时间对废水的组合效应，研究结果对地中海气候条件下的水平潜流人工湿地设计和优化具有重要意义。武弘族等[36]基于GMS建立了泾惠渠灌区月尺度地下水模型，根据地下水年内变化、灌季用水情况以及渠井结合原则，优化设计了不同水平年各灌季渠井用水比例，为灌区保持地下水稳定和水资源高效利用提供技术指导。

（5）参数灵敏度分析。刘瑶林等[21]利用GMS建立了某项目区4层含水层结构的地下水模型，对渗透系数和给水度进行局部、全局灵敏度分析。孙晨等[37]基于裂隙-管道介质物理模型，采用Visual MODFLOW并结合等效渗透系数法建立了地下水模型，通过参数灵敏度分析来研究模型内部结构对泉流量的影响，该成果对岩溶多重介质的泉流量响应规律研究有重要意义。

以上关于地下水数值模拟的应用研究举不胜举，可以预见，随着人们对地下水资源的重视程度以及开发力度的加大，地下水数值模拟研究工作将会更加深入。

4 存在的问题与不足

（1）Visual MODFLOW和GMS对混合井流量模拟精度不足，MODFLOW建议单层井流量大小按各层的导水系数分配，这种做法缺乏依据，与实际不符。

（2）Visual MODFLOW不适合模拟非饱和流、海水入侵等密度变化的地下水流;GMS利用Solid法建立地下水流模型时，对钻孔分布、深度、数量要求高，实际难以达到。

（3）受地下水系统的隐蔽性、复杂性以及实际条件等因素限制，要获取足够准确的数据信息颇为不易，特别是大区域的长系列数据严重不足，这在很大程度上影响了模拟结果的准确性。

（4）目前，地下水数值模拟在岩溶多重含水介质紊流、模型多重耦合、溶质迁移过程中的多种吸附降解作用、多相流动等复杂问题的应用研究仍处于较低水平。

5 结 语

地下水数值模拟技术不论从深度上还是广度上都极大地提高了人们对地下水运动规律的认知，成为解决地下水问题的重要手段。面对越来越复杂的地下水问题和更严格的地下水保护规范，笔者对地下水模拟技术未来的发展趋势提出几点看法。

（1）不断完善模型功能，加强地下水动力学理论研究，实现相关软件的自主研发。

（2）建立完善的水文地质数据库，实现计算机网络社会化服务，避免地质勘探的重复工作。

（3）为提高地下水数值模拟数据处理能力，应加强与信息技术的结合，如地质雷达技术、高密度电阻率探查法、环境同位素技术等。

（4）地下水作为水资源的一种分布状态，与地表水、土壤水、植被、气候以及人类活动都存在一定联系，未来应重点加强地下水与多领域的交叉耦合研究。

参考文献：

[1] 张祥伟，竹内邦良.大区域地下水模拟的理论和方法[J]. 水利学报，2004，35（6）：7-13.

[2] 卢文喜.地下水运动数值模拟过程中边界条件问题探讨[J].水利学报，2003，34（3）：35-38.

[3] WOOD W L. A Noteon How to Avoid Spurious Oscillation in the Finite-Element Solution of the Unsaturated Flow Equation[J]. Journal of Hydrology，1996，176（1-4）：205-218.

[4] KHADRI S F R，PANDE C. Ground Water Flow Modeling for Calibrating Steady State Using MODFLOW Software： A Case Study of Mahesh River Basin，India[J]. Modeling Earth Systems & Environment，2016，2（1）：1-17.

[5] 高小文，吕敬，李秀娟，等.铜矿尾矿库污染物在地下水中运移规律数值模拟[J].水资源与水工程学报，2017，28（2）：120-125.

[6] 齐欢，秦品瑞，丁冠涛.基于GMS的济南市人工补源影响研究[J].灌溉排水学报，2018，37（1）：98-105.

[7] 郑亚楠，吕红宾，胡晓农.基于Visual MODFLOW的地下水流数值模拟：以四川垮梁子滑坡为例[J].人民长江，2018，49（6）： 56-74.

[8] TREFRY M G，MUFFELSC. FEFLOW： A Finite-Element Ground Water Flow and Transport Modeling Tool[J]. Groundwater，2007，45（5）： 525-528.

[9] 丁继红，周德亮，马生忠.国外地下水模拟软件的发展现状与趋势[J].勘察科学技术，2002，32（1）：37-42.

[10] 徐乐昌.地下水模拟常用软件介绍[J].铀矿冶，2002，21（1）：33-38.

[11] 叶伟聪，黑亮，王珊琳.FeFlow和MODFLOW在地下水动态模拟中的应用对比[J].人民珠江，2012，33（6）：77-79.

[12] 何彬.Processing Modflow软件在地下水污染防治中的应用[J].水资源保护，1999，24（3）：16-18.

[13] 刘建国，许光照，马学礼，等.不同模拟软件在地下水环评中的应用对比研究[J].环境科学与技术，2018，41（增刊1）：365-368.

[14] 孙从军，韩振波，赵振，等.地下水数值模拟的研究与应用进展[J].环境工程，2013，31（5）：9-13.

[15] 贺国平，张彤，赵月芬，等.GMS数值建模方法研究综述[J].地下水，2007，29（3）：32-35.

[16] 吴吉春，陆乐.地下水模拟不确定性分析[J].南京大学学报（自然科学版），2011，47（3）：227-234.

[17] 姚兴荣，丁宏伟，沈永平，等.黑河干流拟建水利工程对下游生态环境的影响分析[J].冰川冻土，2012，34（4）：934-941.

[18] 丁际豫，徐鹏飞，陈建平.北京地区地下水盐分迁移变化规律研究[J].环境科学与技术，2017，40（增刊2）：59-64.

[19] 赵丽蓉，黄介生，伍靖伟，等.水管理措施对区域水盐动态的影响[J].水利学报，2011，42（5）：514-522.

[20] 李迎龙，李海明，谢新民，等.基于GMS的沧县地区浅层地下水控制性管理水位研究[J].南水北调与水利科技，2017，15（6）：108-114.

[21] 刘瑶林，刘国东，徐涛，等.多层含水层地下水数值模型参数灵敏度分析[J].环境科学与技术，2014，37（增刊2）：33-37.

[22] 朱君妍，李翠梅，贺靖雄，等.GMS模型的水文水质模拟应用研究[J].水文，2019，39（1）：68-75.

[23] MEHL S，HILL M C. Three-Dimensional Local Grid Refinementfor Block-Centered Finite-Difference Groundwater Models Using Iteratively Coupled Shared Nodes： a New Method of Interpolation and Analysis of Errors[J]. Advances in Water Resources，2004，27（9）：899-912.

[24] KRM David，SRACEK O. MODFLOW-USG： the New Possibilities in Mine Hydrogeology Modeling （or What is Not Written in the Manuals）[J]. Mine Waterand the Environment，2014，33（4）：376-383.

[25] OU G， LI R， PU M， et al. A MODFLOW Package to Linearize Stream Depletion Analysis[J]. Journal of Hydrology，2016，532： 9-15.

[26] NISWONGER R G， PANDAY S， IBARAKI M. MODFLOW-NWT： a Newton Formulation for MODFLOW-2005[J]. US Geological Survey Techniques and Methods，2011，6（37）： 44-51.

[27] KIM N W，CHUNG I M，WON Y S，et al. Development andApplication of the Integrated SWAT-MODFLOW Model[J]. Journal of Hydrology，2008，356（1-2）： 1-16.

[28] MORWAY E D， NISWONGER R G， LANGEVIN C D， et al. Modeling Variably Saturated Subsurface Solute Transport with MODFLOW-UZF and MT3DMS[J]. Groundwater，2013，51（2）： 237-251.

[29] HUGHES J D，LANGEVIN C D，BANTA E R. Documentation for the MODFLOW6 Framework[R]. Ruston，Virginia：US Geological Survey，2017：543-549.

[30] 骆勇，祝晓彬，郭飞，等.不同方法求解疏排水引起的地面沉降对比研究[J].水文地质工程地质，2018，45（5）：156-163.

[31] 曾伟，于茵，缪玮，等.基于Visual MODFLOW的某制药厂地下水环境预测研究[J].工业用水与废水，2018，49（1）：74-78.

[32] 高志鹏，郭华明，屈吉鸿.卫河流域河流-地下水流系统氮素运移的数值模拟[J].地学前缘，2018，25（3）：273-284.

[33] 宫厚健，刘守强，李哲，等.基于Visual Modflow的矿井涌水量数值模拟预测研究[J].煤炭技术，2018，37（8）：155-157.

[34] GOLIAN M，TESHNIZI E S，NAKHAEI M. Prediction of Water Inflowto Mechanized Tunnels During Tunnel-Boring-Machine Advance Using Numerical Simulation[J]. Hydrogeology Journal，2018，26（8）： 2827-2851.

[35] LIOLIOS K A，MOUTSOPOULOS K N，TSIHRINTZIS V A. Comparative Modeling of HSF Constructed Wetland Performance with and Without Evapotranspiration and Rainfall[J]. Environmental Processes，2014，1（2）：171-186.

[36] 武弘族，魏曉妹，降亚楠，等.基于GMS的渠井结合灌区适宜渠井用水比例研究[J].水电能源科学，2017，35（5）：43-46，71.

[37] 孙晨，束龙仓，鲁程鹏，等.裂隙-管道介质泉流量衰减过程试验研究及数值模拟[J].水利学报，2014，45（1）：50-57.

【责任编辑 张华兴】