地下管廊与土体接触的模拟与试验研究

丁天 裴晓峰 孙虎 项长生

摘 要：文章通过Midas GTS利用有限元模拟对地下管廊和土体间的接触进行分析，通过弹塑性支撑来搭建接触界面，利用反作用系数来对地基支撑刚度进行改变，以此来分析地下复合管廊和土体接触面间的关联性，同时通过对土体的内摩擦角作出改变以此来对地下管廓受力情况进行研究。得出土体内摩擦角的改变对地下综合管廊—土体的界面刚度影响很小，界面摩擦角和土体内摩擦角呈正向反馈，扩大土体内的摩擦角将对地下复合廊的强度和变形产生积极影响。根据上述研究表明，可以针对不同质地的土壤通过相对应的措施，对地下复合管廊的沉降和變形达到控制的作用。

关键词：地下综合管廊;土体;沉降变形;接触;Midas GTS

中图分类号：U354 文献标识码：A 文章编号：1001-5922（2021）07-0153-06

Simulation and Experimental Study on the Contact between Underground Pipe Gallery and Soil

Ding Tian1， Pei Xiaofeng1， Sun Hu2， Xiang Changsheng2

（1.China Gansu International Corporation for Economic and Technical Cooperation， Lanzhou 730000，China;

2. School of Civil Engineering， Lanzhou University of Technology，Lanzhou 730000，China）

Abstract：In this paper， Midas GTS uses finite element simulation to analyze the contact between the underground pipe gallery and the soil， and builds the contact interface through elastoplastic support， use the reaction coefficient to change the stiffness of the foundation support to analyze the correlation between the underground composite pipe gallery and the contact surface of the soil， at the same time， the internal friction angle of the soil is changed to study the force of the underground pipe profile. It is concluded that the change of friction angle in soil has little influence on the interfacial rigidity of underground composite pipe gallery-soil， and the magnitude of interfacial friction angle is positively related to the magnitude of friction angle in soil. Expanding the friction angle in soil will positively affect the strength and deformation of underground composite pipe gallery.According to the above research， the settlement and deformation of underground composite pipe gallery can be controlled by corresponding measures for different soil textures.

Key words：underground integrated pipe gallery; soil mass; settlement deformation; contact; Midas GTS

0 引言

地下管道走廊始于1833年，建于巴黎的下水道中。那时，构建良好的卫生系统，对防止城市疾病扩散起着重要作用，并且地下管道的修建和开发也应运而生。西方国家经过一个世纪的发展壮大，所构建的地下复合走廊已经十分成熟，其中法国走在队伍前列，建造的地下管廊公里数位于首位[1]，其由于特殊的管道结构被铺设在地下，而又因地下管廊发生受力和变形时不易被人察觉，因此，社会时刻高度重视地下走廊的安全稳定性。对土体地下管廊力学特性和沉降变形的研究，使得其未来运行和维护能够得到更好地技术支撑，以更有效地促使发展综合地下管廊。Desai等在文献[2-4]上讨论了具有接触损伤的Desai薄膜元件的厚度，而卢廷浩通过对法向以及切向耦合进行测定，对此进行了深入研究，并对薄层单元模型进行了推广[5];唐世斌基于损伤力学构建了接触面模型，考虑了其不均匀性和易损性，得出了剪切损伤是由于高剪应力造成的结论，不均匀性也会在非静态调整过程中产生破坏性应力[6]。邓健采取的方式是通过模拟接触面在演化时弹塑性损伤，结论认为通过模拟接触面的非线性，其精度能够达到工业需求[7-8]。国内目前针对土体等接触做了很多直接剪切实验[9-10]，接触性破坏也在土体中有所体现，而直接剪切实验结果对混凝土或钢板具有较大刚性的损失准确率不高，后续对此还需做进一步研究。

文章通过对地下管廊与土体接触的数值进行模拟可得，土体管廊遭受沉降是受到其内摩擦角和基床系数的影响，针对土体的差异采取不能的解决方式，从而对地下综合管廊的沉降进行控制。

1 理论分析

1.1 接触界面单元

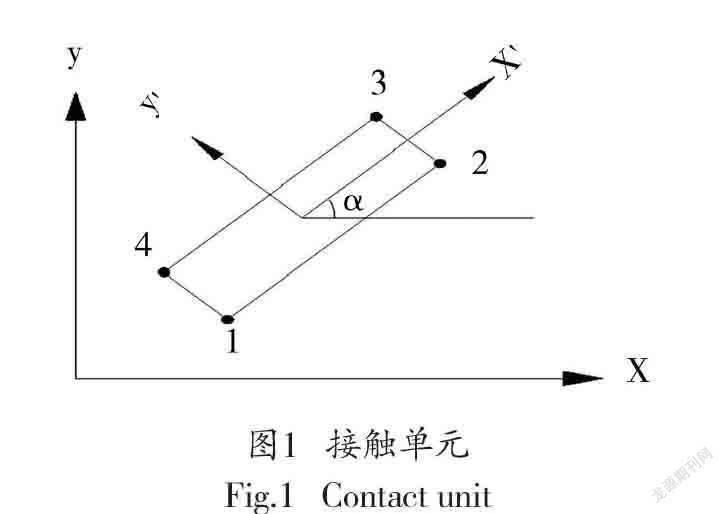
土体和结构之间发生接触是经常存在的，土体的刚度和混凝土的有所区别，二者有着较大差异，即使材料不一致，其接触在有限元软件通过滑动接触元件来完成，Goodman单元被广泛采用[11]。四节点接触如图1所示。

σ为接触单元的正应力，τ为剪应力，二者有着如下关系：

本构关系矩阵D为：

其中kn，ks、分别为轴向刚度和切向刚度，形函数（Ni）如下：

利用参形函数表示单元内任意点位移的公式如下：

接触单元的形函数为：

单元坐标系的位移公式为：

三角函数值可由式（6）微分得到：

定义三角函数为：

应变增量公式为：

其中ue表示所以单元节点位移向量的集合。

B是整体坐标系形函数的微分，对单元坐标系形函数进行微分得到：

则整体坐标系下：

将雅克比矩阵值用于积分转换通过得到：

二维单元的刚度矩阵单元坐标系定义为：

由位移反推应变应力，即可推导出基于摩尔-库伦屈服准则的剪应力为：

1.2 基床系数

基床系数是指假设中基底任随意某点的压强P与该点沉降量S的比值，通常也表示土体的刚度，基床系数Kv通过载荷试验P～S曲线获得，标准承压板的变成一般设置为30cm，而利用非标准承压板所做的载荷试验获取的基床系数需进行数值修正。

黏土：

砂土：

式中，b表示为非标准承压板的边长，Kv1为在非标准承压板试验下进行载荷试验获取的基床系数。

但是现场测试的弊端日益突出，并且测试误差率一直较高，无法满足现场测试需求，室内测试包括3轴和集成测试长时间内也没有参考量，因此基床系数可靠性较低。地基的刚度大多数情况下也可用土体的压缩模量进行表示，压缩模量和基床系数呈正比关系，由于土体基床系数获取的测量值与实际值之间存在很大差异，因此通常使用压缩模量来表示土体刚度。在项目实施进程中，压缩模量根体土体的压缩模量的熟知而设定，从而对土体结构进行分析研究。

2 数值模拟

2.1 有限元模型建立

本文基于无为武威市地下复合管廊，对地下结构和周围土体进行力学分析，将地下管廊埋在3m深处，复合管廊的大小和深度如图2所示。

混凝土强度设置为C30，弹性模量设置为3×104MPa，重度设为25kN/m3，标准段综合管廊宽为8.1m，两外墙厚度取值为0.35m，两内墙墙厚度取值为0.25m，3个舱室宽度从左到右分别为2.9m、2.3m、1.7m;标准段综合管廊高设为4.15m，顶板厚设置为0.35m，底板厚度取值为0.4m，三舱室净高设置为3.4m。综合管廊的底部包括一个10cm的素混凝土防水垫，并从综合管廊的两个外壁延伸10cm。为了对建模过程进行简化，省略了10cm素防水混凝土垫层。

将地下管道放置在半空间主体中，主体大小为20m×15m，将管道土体采用单一土体来代替，通过测量出的内摩擦角和层系数，将其进行对比，同时将接触单元放置在混凝土以及土壤间，具体如图3示意图所示，表1为单一土体参数。

通常，简单的直接剪切测试无法模拟结构与土壤之间的接触行为，由于在现场操作中无法完成简单加载或者循环加载，但是，结构与土体的接触行为对现场直接剪切试验、室内三轴试验和固结试验都适用。接触效应可以通过在混凝土结构和土体间建立接触单元来模拟。

利用Midas GTS NX软件能够完成对地下复合管廊中应力点实施不间断监控，将7个监视点从左到右在其底部依次放置，监视点位于垂直墙和房间中央，图4表示特定监视点所在坐标，图5表示Midas GTS NX中的接触式接口设备的显示，图6表示土体中半无限体模型。

2.2 压缩模量数值分析

表1反应了Midas GTS NX中单个土体的压缩模量变化，调整基床系数，控制土体参数不变，其内摩擦角φ为20°;当前，在地下廊道底面的接触部位上，可以监视7个监察点的垂直力、切向力、垂直位移和切向位移，图7表示垂直力的监控数据;图8表示切向力的监控数据;图9表示法向位移监控数据。

从图7我们可以看出，在7个监视点中，编号1、7垂直力检测数据大致相同，其余5个编号与之相比偏差较大，当土体压缩量从7.45 MPa变为19.45 MPa时，上述监察点的垂直力值几乎保持不变。然而编号1、2、6、7的垂直力呈下降状态，编号3、4、5与之相反，呈上升状态，随着土体压缩模量的上升，这加强了结构中间部分的刚度，并且得出了土体反应模量的上升对结构几乎没有影响。

如图8所示。切向力可为正方向或者是负方向，在7个监视点中，编号2、3方向相同，其余5个编号相同。可以看出法向力的监测值要远远大于同一位置的切向力，并且当土体的压缩模量从7.45 MPa上升到19.45 MPa时，由于每个位置处的切向力都在不断减小，并且降低的值都不是很大，因此土体压缩系数的上升表明对结构几乎没有影响。

在图9中，7个监测点的位移是协同的，几乎不变，并且当土体的压缩模量从7.45MPa上升到19.45MPa时，法向位移标量发生了明显变化，当其从7.45MPa上升到19.45MPa时，垂直位移总体减小了约29.5%;当其从10.45MPa上升到13.45MPa时，垂直位移总体减小了约22.0%，与压缩量是7.45MPa时相比，减小了约44.6%;当其从13.45MPa上升到16.45MPa时，垂直位移总体减小了约18.2%，与压缩量是7.45MPa时相比，减小了约54.6%;当其從16.45MPa上升到19.45MPa时，垂直位移总体减小了约15.4%，与压缩量是7.45MPa时相比，减小了约61.8%;当其值由小变大时，垂直位移总体减少，而减小量则从大到小。地下管廊结构的刚度没有发生改变，接触界面的刚度与土体呈正比关系，土体抵抗结构沉降随着土体的压缩模量增大而变强。该分析表明，地下结构的沉降和变形受坚实的土体影响。

图10表明，切向力可为正方向或者是负方向，每个监测点切向位移数值绝对值均比较小，当压缩模量为7.45 MPa时，监测点2的切向位移相对于其它6个点数值偏大，这是因为此时土体压缩模量过小，界面接触刚度过低，2号监测点所在舱室空间大，整体刚度也较低，故而数值较大;当压缩模量提高至10.45 MPa以后，2号监测点的数值稳定保持较低水平;总体而言，地下管道通道的观察点的切向位移在土体的每个压缩量都是一致的，切向位移的绝对值和地基土体的压缩模量呈反比，土体的压缩模量越大，切向位移越小，这在地下综合管廊的总应力中发挥着积极作用。

2.3 内摩擦角数值分析

控制土体其他参数不变，通过改变表1中的内摩擦角来改变结构—土体界面摩擦角，土体的压缩模量为7.45MPa;在地下廊道底面的接触部位上，可以监视7个监察点的垂直力、切向力、垂直位移和切向位移，图11表示法向力的监测数据;图12表示切向力的监测数据;图13表示垂直位移监测数据;图14表示切向位移监测数据。

图11表明，顺着土体管道走廊的顺序排列的7个观测点的值显示出中间比两边要大的态势;当其内摩擦角从20°变成40°时，每个观察点的垂直位移值不会发生显著变化，具体而言，特定观察点的值变化很小，改变土体摩擦角大小不会显著影响下管道结构的垂直受力形态。

如图12所示。切向力可为正方向或者是负方向，在7个监视点中，编号2、3方向相同，其余5个编号相同，可以看出法向力与切向力都很小，法向力值要远远大于同一位置监测的切向力，当其内摩擦角从20°变成40°时，每个观察点的垂直位移值不会发生显著变化，具体而言，特定观察点的值变化很小，改变土体摩擦角大小不会显著影响下管道结构的水平向受力形态。

图13表明，顺着土体管道走廊的顺序排列的7个观测点的值显示出中间比两边要大的态勢，当土体的内摩擦角从20°增加到40°时，每个观察点的法向位移值不会发生显著变化，然而，总体态势是，土体管道底部的应力条件随着土壤的摩擦角越大变得越强，垂直位移值会略有降低，改变土体摩擦角大小不会显著影响下管道结构的受力形态，但是增加内部摩擦角对地下结构的强度具有正面影响。

图14表明顺着土体管道走廊的顺序排列的7个观测点的垂直位移大体一致，可为正方向或者是负方向，切向位移的绝对值很小，当内摩擦角从20°增加到40°时，每个监视点的切向位移没有明显改变，因此土体内摩擦角对地下综合管廊的切向位移影响可忽略不计。

3 结论

文章通过Midas GTS利用有限元模拟对地下管廊和土体间的接触进行分析，将7个监视点管廊底部底部依次放置，监视点位于垂直墙和房间中央，分别监视垂直力、切向力、垂直位移和切向位移。利用有限元模型，改变土体内摩擦角及压缩模量，对监测结果进行分析，从而得出其对接触面受力的影响，结论如下：

（1）对4节点接触单元进行描述，并给出了界面单元详细的力学计算公式;通过对基床系数和土体压缩模量的简单描述，同时解释了可用压缩模量替代基床系数，并能保证其可靠性;采用地下复合管廊参数在Midas GTS NX中搭建有限元模型，并把7个监控点放置在地下综合管廊与土体间的界面接触单元中。

（2）土壤压缩系数的变化对地下管道的机械状态机会无影响，对切向位移的也影响甚微，法向位移则会受到明显影响，法向位移和压缩模量呈反比关系，增加土体压缩模量对综合管廊的强度和变形具有正面影响;改变土体摩擦角大小不会显著影响综合管廊的受力形态，对法向位移、切向位移数值的也影响甚微，但是增加内摩擦角对综合管廊的强度和变形具有正面影响。

参考文献

[1]于晨龙，张作慧.国内外城市地下综合管廊的发展历程及现状[J].建设科技，2015，179（12）：49-51.

[2]C.S.Desai，B.K.Nagaraj. Modeling for cyclic normal and shear behavior of interfaces[J]. Journal of Engineering Mechanics，1988，114（7）：1198-1217.

[3]Brandt J R T.Behavior of soil-concrete interfaces[M].Canda： The University of Alberta， 1985.

[4]K.G.Sharma，C.S.Desai.Analysis and implementation of thin-layer element for interfaces and joints[J].Journal of Engineering Mechanics，1992，118（12）：2442-2462.

[5]卢廷浩，鲍伏波.接触面单元薄层耦合本构模型[J].水利学报，2000，02：71-75.

[6]唐世斌，唐春安，梁正召.接触面损伤演化过程的数值模拟[J].计算力学学报，2011，28（1）： 146-151.

[7]邓建，肖明，谢冰冰.三维接触面单元弹塑性损伤数值模拟分析方法[J].中南大学学报（自然科学版）， 2016，47（7）：2383-2389.

[8]Fredlund D G，Rahadjo H.Soil mechanics for unsaturated soil mechanics[M].New York：John Wiley and Sons，1993.

[9]Evgin E，Fakharian K.Effect of stress paths on the behavior of sand-steel interfaces[J]. Canadian Geotechnical Journal，1996，33（33）：853-865.

[10]Uesugi M，Kishida H.Influential factors of between steel and dry sands[J].Soils and Foundations，1986，26（2）：33-46.

[11]胡黎明，濮家骝.土与结构物接触面损伤本构模型[J].岩土力学，2002，23（1）：6-11.